1.2直角三角形（2）课件

课件22张PPT。2.直角三角形（2）
直角三角形全等的证明公理:三边对应相等的两个三角形全等（SSS）.
公理:两边及其夹角对应相等的两个三角形全等（SAS）.
公理:两角及其夹边对应相等的两个三角形全等（ASA）.
推论:两角及其中一角的对边对应相等的两个三角形全等（AAS）.想一想:
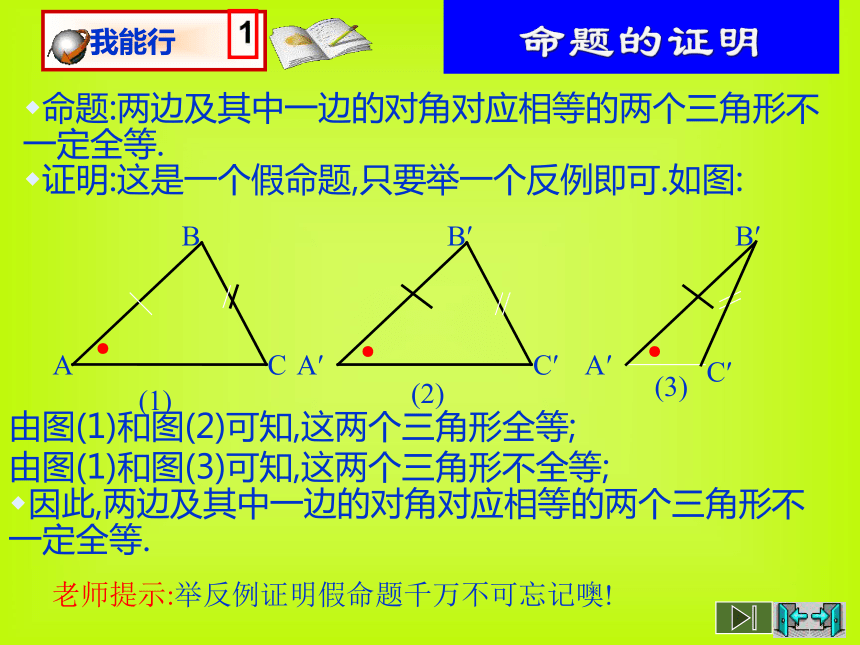
两边及其中一边的对角对应相等的两个三角形全等?两边及其中一边的对角对应相等的两个三角形不一定全等.如果其中一边的所对的角是直角呢?如果其中一边的所对的角是直角,那么这两个三角形全等.请证明你的结论.命题:两边及其中一边的对角对应相等的两个三角形不一定全等.老师提示:举反例证明假命题千万不可忘记噢!证明:这是一个假命题,只要举一个反例即可.如图:由图(1)和图(2)可知,这两个三角形全等;
由图(1)和图(3)可知,这两个三角形不全等;
因此,两边及其中一边的对角对应相等的两个三角形不一定全等.′两边及其中一边的对角对应相等的两个三角形不一定全等.但如果其中一组等边所对的角是直角,那么这两个三角形全等.老师期望:你能写出它的证明过程吗?
你能用根据上面的证明用文字写出一个结论吗?已知:如图,在△ABC和△A′B′C′中, AC=A′C ′, AB=A′B′, ∠C=∠C′=900.
求证:△ABC≌△A′B′C′.分析:
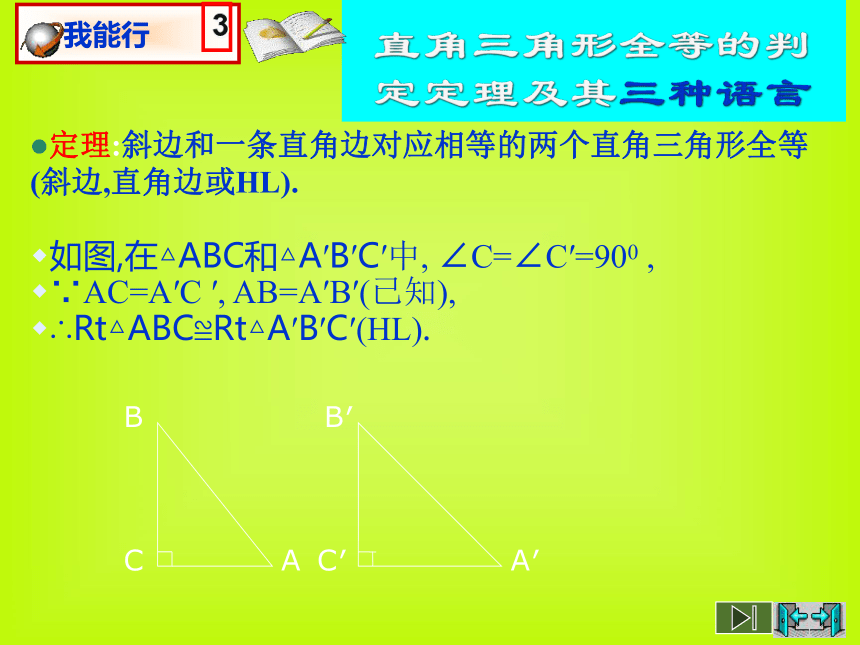
要证明△ABC≌△A′B′C′ ,只要能满足公理(SSS),(SAS),(ASA)和推论(AAS)中的一个即可.由已知和根据勾股定理易知,第三条边也对应相等.定理:斜边和一条直角边对应相等的两个直角三角形全等(斜边,直角边或HL).如图,在△ABC和△A′B′C′中, ∠C=∠C′=900 ,
∵AC=A′C ′, AB=A′B′(已知),
∴Rt△ABC≌Rt△A′B′C′(HL). 直角三角形全等的判定定理
定　　理：_________和______________________的两个直角三角形全等．
说　　明：(1)此定理可以简写成“斜边、直角边”或“HL”；
(2)此定理是直角三角形所独有的，对一般三角形不成立．
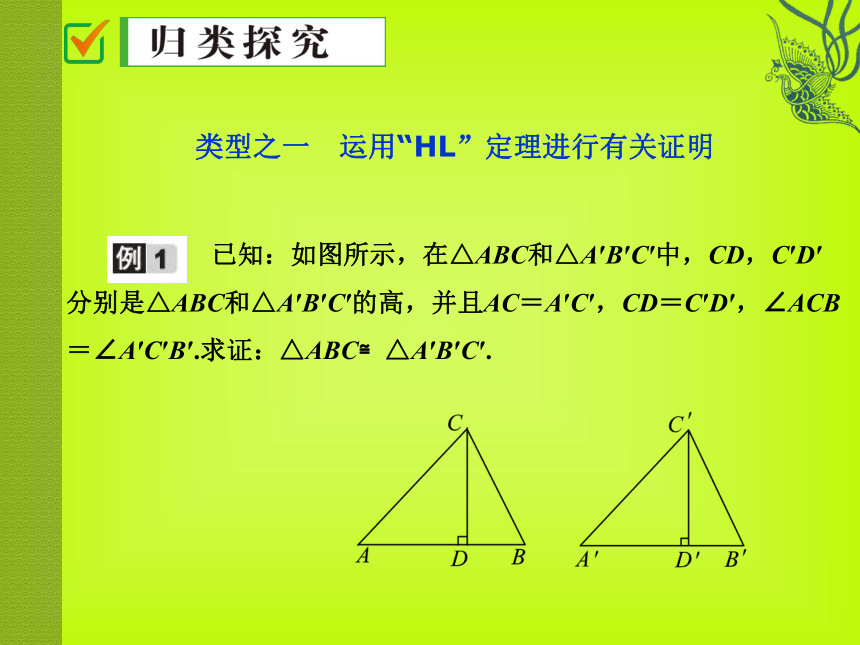
作　　用：判定两个直角三角形全等．知 识 管 理 斜边一条直角边分别相等 已知：如图所示，在△ABC和△A′B′C′中，CD，C′D′分别是△ABC和△A′B′C′的高，并且AC＝A′C′，CD＝C′D′，∠ACB＝∠A′C′B′.求证：△ABC≌△A′B′C′.类型之一　运用“HL”定理进行有关证明证明： 在Rt△ADC和Rt△A′D′C′ 中，
∠ADC＝∠A′D′C′＝90°.
∵AC＝A′C′，CD＝C′D′，
∴Rt△ADC≌Rt△A′D′C′(HL)，
∴∠A＝∠A′(全等三角形对应角相等)．
又∵∠ACB＝∠A′C′B′，AC＝A′C′，
∴△ABC≌△A′B′C′(ASA)．类型之二　
直角三角形全等的判定在实际生活中的应用
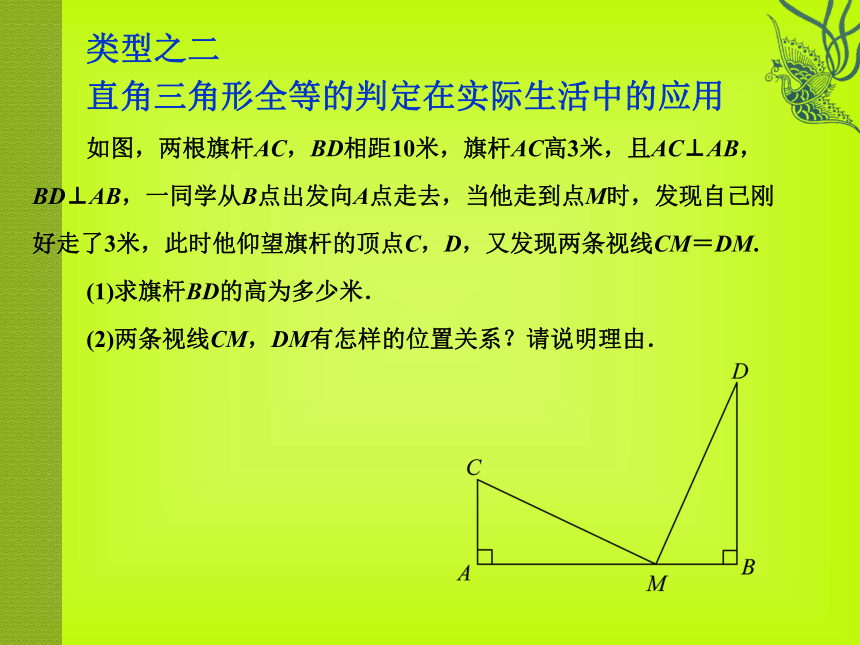
如图，两根旗杆AC，BD相距10米，旗杆AC高3米，且AC⊥AB，BD⊥AB，一同学从B点出发向A点走去，当他走到点M时，发现自己刚好走了3米，此时他仰望旗杆的顶点C，D，又发现两条视线CM＝DM.
(1)求旗杆BD的高为多少米．
(2)两条视线CM，DM有怎样的位置关系？请说明理由．【解析】 (1)根据HL定理得出Rt△ACM≌Rt△BMD，进而得出AM＝BD，进而得出BD的长即可；
(2)利用Rt△ACM≌Rt△BMD，则∠C＝∠BMD，进而得出∠BMD＋∠AMC＝90°，即可得出答案．(2)CM⊥DM.
理由：由(1)知Rt△ACM≌Rt△BMD，
∴∠C＝∠BMD.
∵∠C＋∠AMC＝90°，
∴∠BMD＋∠AMC＝90°，
∴∠CMD＝90°，
∴CM⊥DM.
1．[2012·巴中]如图1－2－12，已知AD是△ABC的边BC上的高，下列能使△ABD≌△ACD的条件是 (　 　)
A．AB＝AC　　　　　　　B．∠BAC＝90°
C．BD＝AC D．∠B＝45°图1－2－12A2．下列选项中的直角三角形与图1－2－13所示的直角三角形全等的是 (　 　)图1－2－13图1－2－14A　　　　B　　　C　　　　D　B3．已知两个直角三角形全等，其中一个直角三角形的面积为3，斜边长为4，则另一个直角三角形斜边上的高是 (　 　) 【解析】 全等三角形的对应高相等．C4．如图1－2－15所示，∠A＝∠D＝90°，AB＝DC＝3，AC＝6，求△DBC的面积．图1－2－15蓄势待发如图,已知∠ACB=∠BDA=900 , 要使△ABC≌△BDA, 还需要什么条件?把它们分别写出来.增加AC=BD;增加BC=AD;增加∠ABC=∠BAD ;增加∠CAB=∠DBA ;你能分别写出它们的证明过程吗?若AD,BC相交于点O,图中还有全等的三角形吗?O你能写出图中所有相等的线段,相等的角吗?你能分别写出它们的证明过程吗?知识在于积累判断下列命题的真假,并说明理由:两个锐角对应相等的两个直角三角形全等;斜边及一个锐角对应相等的两个直角三角形全等;两直角边对应相等的两个直角三角形全等;一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.回味无穷直角三角形全等的判定定理:
定理:斜边和一条直角边对应相等的两个直角三角形全等(斜边,直角边或HL).
公理:三边对应相等的两个三角形全等（SSS）.
公理:两边及其夹角对应相等的两个三角形全等（SAS）.
公理:两角及其夹边对应相等的两个三角形全等（ASA）.
推论:两角及其中一角的对边对应相等的两个三角形全等（AAS）.
综上所述,直角三角形全等的判定条件可归纳为:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;
切记!!!命题:两边及其中一边的对角对应相等的两个三角形不一定全等.1.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.
求证: △ABC是等腰三角形. 分析:要证明△ABC是等腰三角形,就需要证明AB=AC; 进而需要证明∠B∠C所在的△BDF≌△CDE;而△BDF≌△CDE的条件: 从而需要证明∠B=∠C; BD=CD,DF=DE均为已知.因此, △ABC是等腰三角形可证.老师期望:
请将证明过程规范化书写出来.驶向胜利的彼岸2.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF.
求证:(1)AE=AF;(2)AB∥CD. 老师期望:请将证明过程规范化书写出来. 分析:(1)要证明AE=CF,由此AE=CF可证. 需要证明内错角∠A=∠C;而由△ABF≌△CDE可得证. (2)要证明AB∥CD, 由已知条件, AB=CD,DE⊥AC,BF⊥AC, DE=BF.可证得△ABF≌△CDE,从而可得AF=CE.结束寄语严格性之于数学家,犹如道德之于人.
证明的规范性在于：条理清晰，因果相应,言必有据.这是初学证明者谨记和遵循的原则.