第七章 二次根式专项训练 特殊四边形与二次根式的运算(含答案)
文档属性
| 名称 | 第七章 二次根式专项训练 特殊四边形与二次根式的运算(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
特殊四边形与二次根式的运算
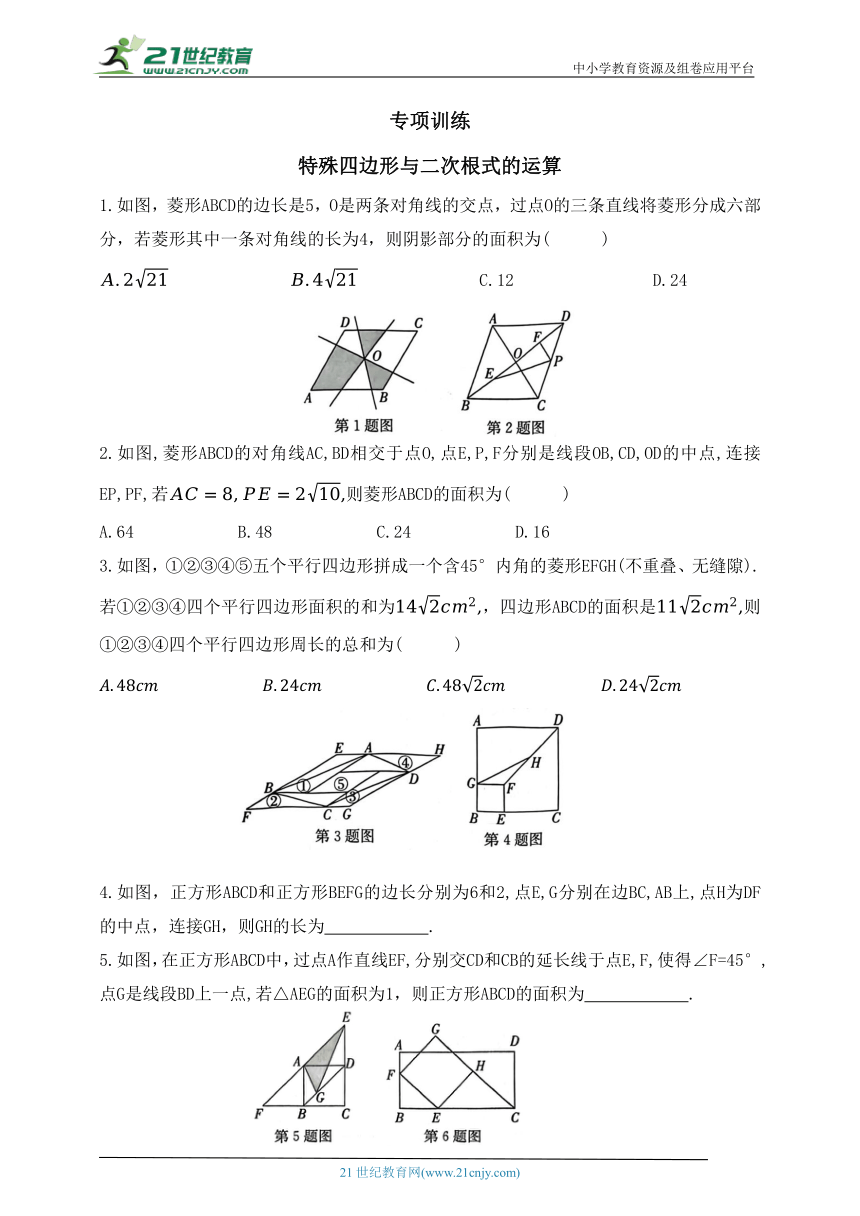
1.如图,菱形ABCD的边长是5,O是两条对角线的交点,过点O的三条直线将菱形分成六部分,若菱形其中一条对角线的长为4,则阴影部分的面积为( )
C.12 D.24
2.如图,菱形ABCD的对角线AC,BD相交于点O,点E,P,F分别是线段OB,CD,OD的中点,连接EP,PF,若则菱形ABCD的面积为( )
A.64 B.48 C.24 D.16
3.如图,①②③④⑤五个平行四边形拼成一个含45°内角的菱形EFGH(不重叠、无缝隙).若①②③④四个平行四边形面积的和为,四边形ABCD的面积是则①②③④四个平行四边形周长的总和为( )
4.如图,正方形ABCD和正方形BEFG的边长分别为6和2,点E,G分别在边BC,AB上,点H为DF的中点,连接GH,则GH的长为 .
5.如图,在正方形ABCD中,过点A作直线EF,分别交CD和CB的延长线于点E,F,使得∠F=45°,点G是线段BD上一点,若△AEG的面积为1,则正方形ABCD的面积为 .
6.如图,在矩形ABCD中,AB=4,BC=8,点E 在BC边上,且BE=3,F为AB边上的一个动点,连接EF,以EF为边作正方形EFGH,且点H在矩形ABCD内,连接CH,则CH 的最小值为 .
7.如图,△ABC中,D,E分别为AB,BC的中点,DG⊥AC,EF⊥AC,垂足分别为G,F.
(1)求证:四边形DEFG为矩形.
(2)若求CF的长.
参考答案
1.A
2.B [解析]∵四边形ABCD是菱形,∴AC⊥BD,OA=OC.OB=OD.
∵点E,P,F分别是线段OB,CD,OD的中点
2EF=12,
∴菱形ABCD是面积 12=48.
3.A [解析]如图,作GM⊥EF于点M.由题意得∴
又∵∠F=45°,设菱形的边长为xcm,则菱形的高GM
根据菱形的面积公式得 解得x=6,∴菱形的边长为6cm,
∴①②③④四个平行四边形周长的总和
5.2 [解析]如图,过点D作DH⊥EF于点H.
∵四边形ABCD是正方形,∴∠C=∠ADC=∠ADE=90°,∠DBC =45°.
∵∠F=45°,∴∠E=180°-∠F-∠C=45°,∴BD ∥EF,∴△ADE是等腰直角三角形.
设正方形ABCD的边长为m,则
的面积为1, 即
∴正方形ABCD的面积为2.
[解析]如图,过点H作HM⊥BC于点M.
∵四边形EFGH是正方形,∴EF=HE,∠FEH=90°,∴∠BEF +∠MEH=∠MEH +∠MHE= 90°,
∴∠BEF=∠MHE.
∵四边形ABCD是矩形,∴∠B=90°=∠EMH,∴△BEF≌△MHE(AAS),∴BE=HM=3,BF=EM.
设BF=EM=x,则CM=BC-BE-EM=8-
.当x=4时,CH有最小值为
7.(1)证明:∵点D是AB的中点,点E是BC的中点,∴DE是△ABC的中位线,∴DE∥AC.
∵DG⊥AC,EF⊥AC,∴EF∥DG,∴四边形DEFG是平行四边形.
又∵DG⊥AC,∴四边形DEFG为矩形.
(2)解:EF=2,点E是BC的中点,
由(1)知四边形DEFG为矩形,则
在Rt△ADG中,
由勾股定理得AG=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
特殊四边形与二次根式的运算
1.如图,菱形ABCD的边长是5,O是两条对角线的交点,过点O的三条直线将菱形分成六部分,若菱形其中一条对角线的长为4,则阴影部分的面积为( )
C.12 D.24
2.如图,菱形ABCD的对角线AC,BD相交于点O,点E,P,F分别是线段OB,CD,OD的中点,连接EP,PF,若则菱形ABCD的面积为( )
A.64 B.48 C.24 D.16
3.如图,①②③④⑤五个平行四边形拼成一个含45°内角的菱形EFGH(不重叠、无缝隙).若①②③④四个平行四边形面积的和为,四边形ABCD的面积是则①②③④四个平行四边形周长的总和为( )
4.如图,正方形ABCD和正方形BEFG的边长分别为6和2,点E,G分别在边BC,AB上,点H为DF的中点,连接GH,则GH的长为 .
5.如图,在正方形ABCD中,过点A作直线EF,分别交CD和CB的延长线于点E,F,使得∠F=45°,点G是线段BD上一点,若△AEG的面积为1,则正方形ABCD的面积为 .
6.如图,在矩形ABCD中,AB=4,BC=8,点E 在BC边上,且BE=3,F为AB边上的一个动点,连接EF,以EF为边作正方形EFGH,且点H在矩形ABCD内,连接CH,则CH 的最小值为 .
7.如图,△ABC中,D,E分别为AB,BC的中点,DG⊥AC,EF⊥AC,垂足分别为G,F.
(1)求证:四边形DEFG为矩形.
(2)若求CF的长.
参考答案
1.A
2.B [解析]∵四边形ABCD是菱形,∴AC⊥BD,OA=OC.OB=OD.
∵点E,P,F分别是线段OB,CD,OD的中点
2EF=12,
∴菱形ABCD是面积 12=48.
3.A [解析]如图,作GM⊥EF于点M.由题意得∴
又∵∠F=45°,设菱形的边长为xcm,则菱形的高GM
根据菱形的面积公式得 解得x=6,∴菱形的边长为6cm,
∴①②③④四个平行四边形周长的总和
5.2 [解析]如图,过点D作DH⊥EF于点H.
∵四边形ABCD是正方形,∴∠C=∠ADC=∠ADE=90°,∠DBC =45°.
∵∠F=45°,∴∠E=180°-∠F-∠C=45°,∴BD ∥EF,∴△ADE是等腰直角三角形.
设正方形ABCD的边长为m,则
的面积为1, 即
∴正方形ABCD的面积为2.
[解析]如图,过点H作HM⊥BC于点M.
∵四边形EFGH是正方形,∴EF=HE,∠FEH=90°,∴∠BEF +∠MEH=∠MEH +∠MHE= 90°,
∴∠BEF=∠MHE.
∵四边形ABCD是矩形,∴∠B=90°=∠EMH,∴△BEF≌△MHE(AAS),∴BE=HM=3,BF=EM.
设BF=EM=x,则CM=BC-BE-EM=8-
.当x=4时,CH有最小值为
7.(1)证明:∵点D是AB的中点,点E是BC的中点,∴DE是△ABC的中位线,∴DE∥AC.
∵DG⊥AC,EF⊥AC,∴EF∥DG,∴四边形DEFG是平行四边形.
又∵DG⊥AC,∴四边形DEFG为矩形.
(2)解:EF=2,点E是BC的中点,
由(1)知四边形DEFG为矩形,则
在Rt△ADG中,
由勾股定理得AG=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
