2.1.1 圆的标准方程 课件(共21张PPT)
文档属性
| 名称 | 2.1.1 圆的标准方程 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
导入新课
评价分析
教法分析
一石激起千层浪
圆
圆是自然界最完美的曲线之一.
2.1.1 圆的标准方程
问题一:初中时我们是怎样给圆下定义的?
平面上到定点的距离等于定长的点的集合(轨迹)是圆。
A
r
复习提问、导入新课
评价分析
教材析
目标分析
o
y
x
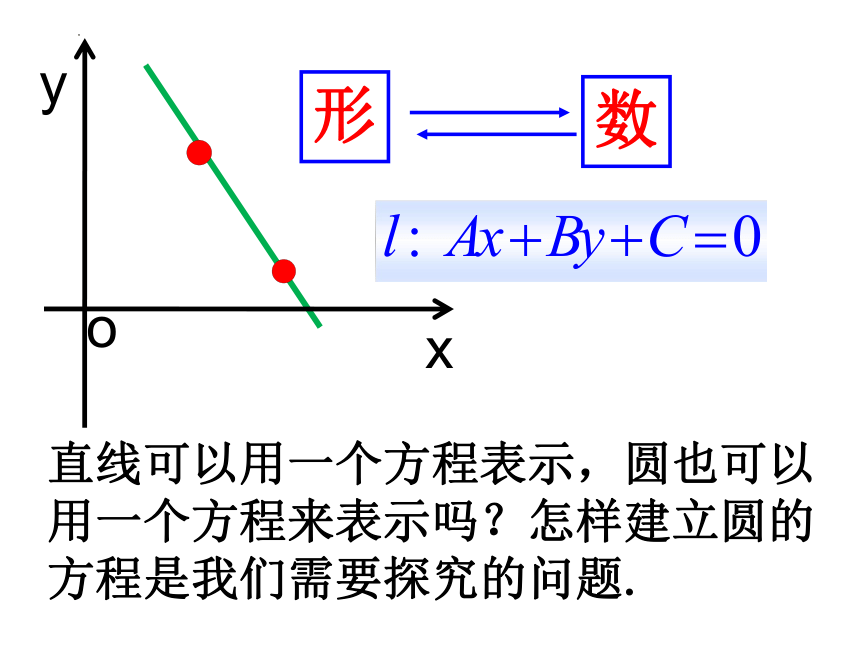
形
数
直线可以用一个方程表示,圆也可以用一个方程来表示吗?怎样建立圆的方程是我们需要探究的问题.
合作探究
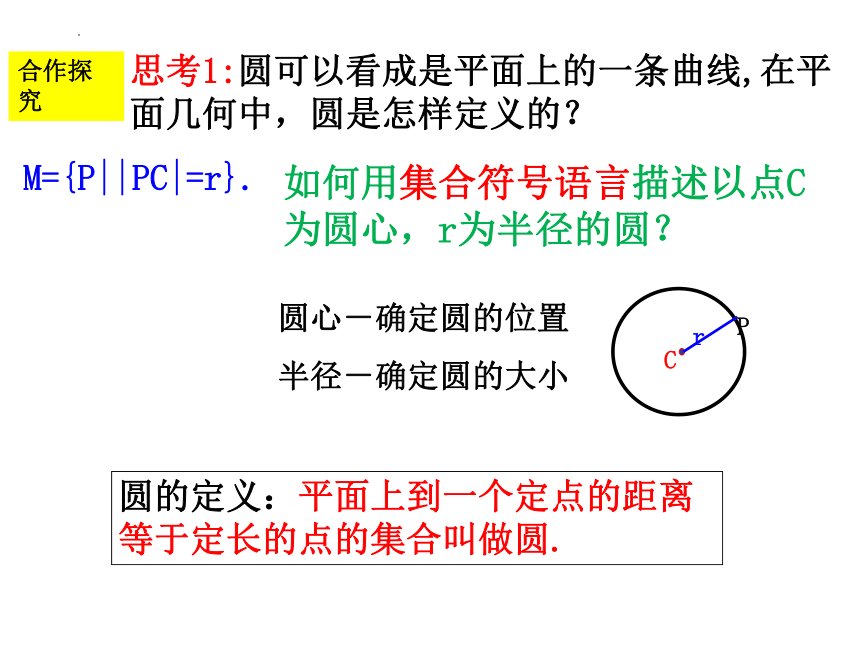
如何用集合符号语言描述以点C为圆心,r为半径的圆?
思考1:圆可以看成是平面上的一条曲线,在平面几何中,圆是怎样定义的?
圆的定义:平面上到一个定点的距离等于定长的点的集合叫做圆.
C
P
r
M={P||PC|=r}.
圆心-确定圆的位置
半径-确定圆的大小
圆的标准方程
1、建系如图;
2、设点M(x, y)为圆上
任意一点;
x
y
O
C
M(x,y)
3、限定条件
|MC|= R
4、代点;
5、化简;
建
设
限
代
化
x
y
O
C
M(x,y)
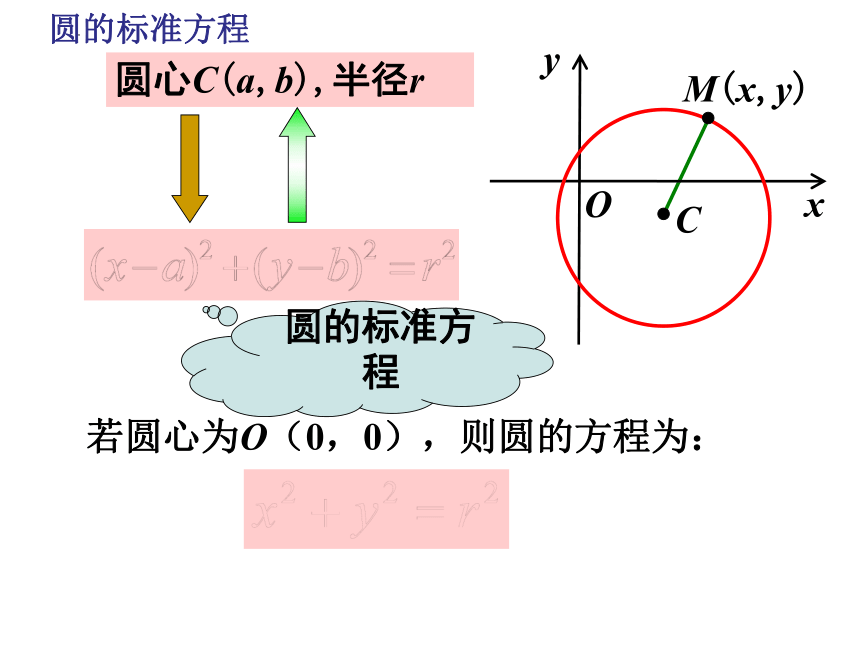
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
圆的标准方程
圆的标准方程
写出下列各圆的圆心坐标和半径:
(1) (x-1)2+y2=6
(2) (x+1)2+(y-2)2=9
(3)(x+a)2+y2=a2(a≠0)
(4)点A(3,4),B(3,5),C(3,3)都在圆x2+y2=25吗
(1,0)
6
(-1,2) 3
(-a,0) |a|
看清楚了,这里是字母!它有自己的正负性
在圆上
在圆外
在圆内
口答:
例1.说出下列圆的方程:
(1) 圆心在原点,半径为3.
(2) 圆心在点C(3, -4), 半径为7.
解:(1) 圆心为(0,0),半径为3
所以a=0,b=0,r=3
圆的标准方程为 (x -0)2 + ( y 0)2 = 32
即x 2 + y 2 = 9
解:(2) 圆心为(3,-4),半径为7
所以a=3,b=-4,r=7
圆的标准方程为 (x -3)2 + 【 y (-4)】2 = 72
即 (x -3)2 + (y + 4)2 = 49
灵活应用,能力提升
变式1 求圆心为(2,-1),与直线x+y=6相切的圆的标准方程。
应用举例、巩固提高
例2 求圆心为C(8,-3),过点P(5, 1)的圆的标准方程。
评价分析
教法分析
过程分析
教材分析
灵活应用,能力提升
变式2 已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线 l:x -y +1=0上,求圆的标准方程。
应用举例、巩固提高
例3 △ABC的三个顶点坐标分 别是A(5,1)、B(7,-3)、C(2,-8),求其外接圆的标准方程。
评价分析
教法分析
过程分析
教材分析
目标分析
课堂小结
(1)直接法
根据已知条件,直接求出圆心坐标和圆的半径,然后写出圆的方程.
求解圆的标准方程方法:
(2)待定系数法
①根据题意,设出标准方程;
②根据条件,列关于a,b,r的方程组;
③解出a,b,r,代入标准方程.
怎样判断点 在圆 内呢?圆上?还是在圆外呢?
探究
C
x
y
o
M1
M2
M3
数学建构
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系 利用距离判断 利用方程判断
点M在圆上 CM=r (x0-a)2+(y0-b)2 r2
点M在圆外 CM>r (x0-a)2+(y0-b)2 r2
点M在圆内 CM=
>
<
练习 点P(1,-1)在圆(x+2)2+y2=m的外部,则实数m的取值范围是________.
能力提高
1.已知A(-2,0),B(2,0),求过A,B两点的半径最小的圆的方程.
2.求过A(2,0),半径为2的圆的圆心的轨迹方程.
3.求过点A(-1,3),面积为49π的圆的圆心的轨迹方程.
圆心C(a,b),半径r
x
y
O
C
A
B
C
1.圆的标准方程
2.圆心
①两条直线的交点
(弦的垂直平分线)
②直径的中点
3.半径
①圆心到圆上一点
②圆心到切线的距离
小结
小结
4.点与圆的位置关系
(1)点P在圆上
(2)点P在圆内
(3)点P在圆外
谢谢!
导入新课
评价分析
教法分析
一石激起千层浪
圆
圆是自然界最完美的曲线之一.
2.1.1 圆的标准方程
问题一:初中时我们是怎样给圆下定义的?
平面上到定点的距离等于定长的点的集合(轨迹)是圆。
A
r
复习提问、导入新课
评价分析
教材析
目标分析
o
y
x
形
数
直线可以用一个方程表示,圆也可以用一个方程来表示吗?怎样建立圆的方程是我们需要探究的问题.
合作探究
如何用集合符号语言描述以点C为圆心,r为半径的圆?
思考1:圆可以看成是平面上的一条曲线,在平面几何中,圆是怎样定义的?
圆的定义:平面上到一个定点的距离等于定长的点的集合叫做圆.
C
P
r
M={P||PC|=r}.
圆心-确定圆的位置
半径-确定圆的大小
圆的标准方程
1、建系如图;
2、设点M(x, y)为圆上
任意一点;
x
y
O
C
M(x,y)
3、限定条件
|MC|= R
4、代点;
5、化简;
建
设
限
代
化
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
圆的标准方程
圆的标准方程
写出下列各圆的圆心坐标和半径:
(1) (x-1)2+y2=6
(2) (x+1)2+(y-2)2=9
(3)(x+a)2+y2=a2(a≠0)
(4)点A(3,4),B(3,5),C(3,3)都在圆x2+y2=25吗
(1,0)
6
(-1,2) 3
(-a,0) |a|
看清楚了,这里是字母!它有自己的正负性
在圆上
在圆外
在圆内
口答:
例1.说出下列圆的方程:
(1) 圆心在原点,半径为3.
(2) 圆心在点C(3, -4), 半径为7.
解:(1) 圆心为(0,0),半径为3
所以a=0,b=0,r=3
圆的标准方程为 (x -0)2 + ( y 0)2 = 32
即x 2 + y 2 = 9
解:(2) 圆心为(3,-4),半径为7
所以a=3,b=-4,r=7
圆的标准方程为 (x -3)2 + 【 y (-4)】2 = 72
即 (x -3)2 + (y + 4)2 = 49
灵活应用,能力提升
变式1 求圆心为(2,-1),与直线x+y=6相切的圆的标准方程。
应用举例、巩固提高
例2 求圆心为C(8,-3),过点P(5, 1)的圆的标准方程。
评价分析
教法分析
过程分析
教材分析
灵活应用,能力提升
变式2 已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线 l:x -y +1=0上,求圆的标准方程。
应用举例、巩固提高
例3 △ABC的三个顶点坐标分 别是A(5,1)、B(7,-3)、C(2,-8),求其外接圆的标准方程。
评价分析
教法分析
过程分析
教材分析
目标分析
课堂小结
(1)直接法
根据已知条件,直接求出圆心坐标和圆的半径,然后写出圆的方程.
求解圆的标准方程方法:
(2)待定系数法
①根据题意,设出标准方程;
②根据条件,列关于a,b,r的方程组;
③解出a,b,r,代入标准方程.
怎样判断点 在圆 内呢?圆上?还是在圆外呢?
探究
C
x
y
o
M1
M2
M3
数学建构
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系 利用距离判断 利用方程判断
点M在圆上 CM=r (x0-a)2+(y0-b)2 r2
点M在圆外 CM>r (x0-a)2+(y0-b)2 r2
点M在圆内 CM
>
<
练习 点P(1,-1)在圆(x+2)2+y2=m的外部,则实数m的取值范围是________.
能力提高
1.已知A(-2,0),B(2,0),求过A,B两点的半径最小的圆的方程.
2.求过A(2,0),半径为2的圆的圆心的轨迹方程.
3.求过点A(-1,3),面积为49π的圆的圆心的轨迹方程.
圆心C(a,b),半径r
x
y
O
C
A
B
C
1.圆的标准方程
2.圆心
①两条直线的交点
(弦的垂直平分线)
②直径的中点
3.半径
①圆心到圆上一点
②圆心到切线的距离
小结
小结
4.点与圆的位置关系
(1)点P在圆上
(2)点P在圆内
(3)点P在圆外
谢谢!
