(2023春)人教版五年级数学下册 第5课时 长方体和正方体的体积(课件)(共28张PPT)
文档属性
| 名称 | (2023春)人教版五年级数学下册 第5课时 长方体和正方体的体积(课件)(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 09:12:15 | ||
图片预览





文档简介
(共28张PPT)
2023春人教版 数学
五年级下册
3 长方体和正方体
3.5 长方体和正方体的体积
1. 小组合作动手操作推导出长方体、正方体的体积公式。(重点)
2. 应用长方体和正方体的体积计算公式解决实际问题。(难点)
学习目标
回顾复习
(1)物体所占空间的大小叫作物体的( )。
(2)计量体积要用体积单位,常用的体积单位有( )、( )和( ),
可以分别写成( )、( )和( ) 。
体积
立方厘米
立方分米
立方米
cm3
dm3
m3
1. 填一填。
回顾复习
2. 判断,并说明理由。
体积为1立方米的立体图形一定是棱长为1米的正方体。 ( )
×
理由:
据体积的意义,物体所占空间的大小叫做物体的体积。体积是1立方米的立体图形可能是正方体,也可能是长方体或其它形体。
(教材P29 例题)
探索新知
求长方体的体积就是看长方体有多少个体积单位。
把长方体分成若干单位体积的小正方体,就可以……
讨论一下:怎样计算长方体的体积?
探索新知
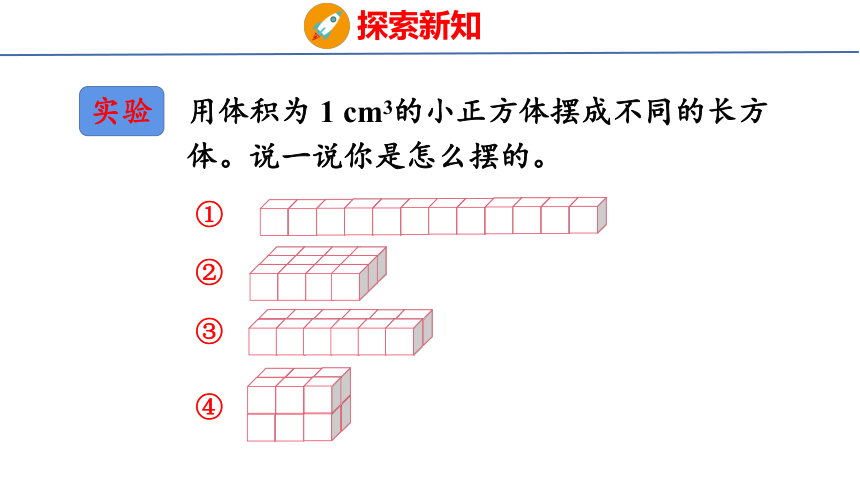
实验
用体积为 1 cm3的小正方体摆成不同的长方体。说一说你是怎么摆的。
②
①
③
④
探索新知
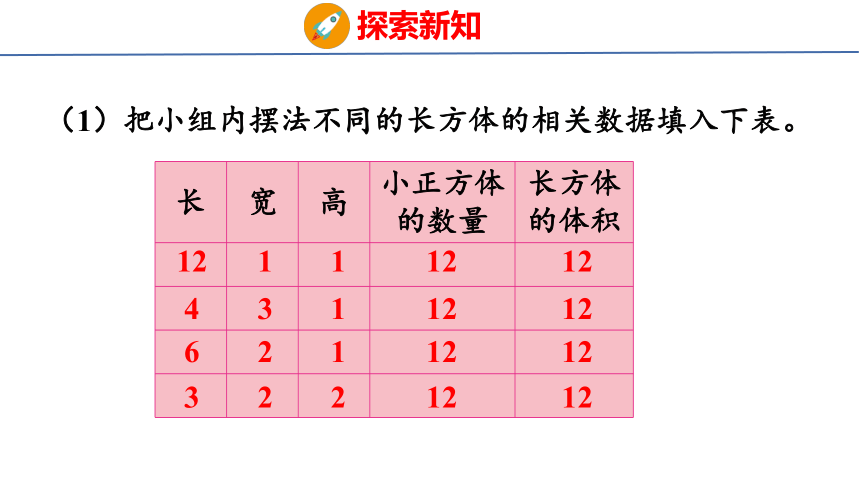
(1)把小组内摆法不同的长方体的相关数据填入下表。
长 宽 高 小正方体的数量 长方体的体积
12
1
1
12
12
4
3
1
12
12
6
2
1
12
12
3
2
2
12
12
探索新知
观察上表:摆出的长方体的体积与长、宽、高有什么关系?
长方体所含体积单位的个数就是长方体的体积。
长方体的体积正好等于长×宽×高的积。
探索新知
长方体的体积=长×宽×高
V=a b h
如果用字母V表示长方体的体积,用a,b,h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:
a
b
h
探索新知
根据长方体和正方体的关系,想一想正方体的体积怎样计算。
如果用字母V表示正方体的体积,用a表示它的棱长,那么正方体的体积计算公式可以写成:
V=a · a · a
a
探索新知
正方体的体积公式一般写成: V=a3
a·a·a也可以写作“a3”,读作“a的立方”,表示3个a相乘。
探索新知
1
(教材P30 例1)
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
V=a b h
=6×5×4
=120(dm3)
V=a3
=53
=5×5×5
=125(dm3)
6
5
4
5
5
5
探索新知
长方体或正方体底面的面积叫做底面积。
底面
底面
长方体的体积=长×宽×高
底面积
正方体的体积=棱长×棱长×棱长
底面积
探索新知
所以,长方体和正方体的体积也可以这样来计算:
长方体(或正方体)的体积=底面积×高
如果用字母S表示底面积,上面的公式可以写成:
V=Sh
S
h
随堂小练
做一做
1. 一块长方体豆腐的尺寸如下图所示,它的体积是多少?
(教材P31做一做 第1题)
V=a b h
=15×7×5
=525(cm3)
答:它的体积是525 cm3。
随堂小练
做一做
2. 一根长方体木料,长5 m,横截面的面积是0.06 m2。这根木料的体积是多少 (教材P31做一做 第2题)
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06 m2
当堂检测
1. 填空。
(1)一个正方体的棱长为 5 cm,它的体积是
_________。
(2)一个长方体纸盒,长 6 dm,宽 5 dm,高
7 dm,它的体积是______dm3。
125cm3
210
当堂检测
30×30×30 = 27000(cm3)
答:它的体积是27000 cm3。
2. 一块棱长 30 cm 的正方体冰块,它的体积是多少
立方厘米?(教材P33练习七 第9题)
当堂检测
3. 家具厂订购500根方木,每根方木横截面的面
积是2.4 dm2,长是3 m。这些方木一共是多
少立方米 (教材P33练习七 第11题)
当堂检测
2.4 dm2=0.024 m2
0.024×3×500=36(m3)
36 m3=36(m3)
答:这些木料一共是36立方米。
当堂检测
4. 判断:
棱长是6 cm的正方体,体积和表面积相等。
( )
错解:√
当堂检测
错因分析:本题错在只看计算结果的数据,没看数据的单位。体积是216 cm3,表面积是216 cm2,两者表示的意义不同,不能比较。体积和表面积不是同类量,两者之间不能比较。
正解:×
学习完本节课,你有什么收获?
课堂小结
通过本节课的学习,我们掌握了长方体、正方体的体积公式。
课堂小结
课堂小结
长方体和正方体的体积公式:
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×棱长
V=a3
a
a
b
h
课堂小结
长方体和正方体体积的统一公式:
长方体(或正方体)的体积=底面积×高
V = Sh
S
h
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
2023春人教版 数学
五年级下册
3 长方体和正方体
3.5 长方体和正方体的体积
1. 小组合作动手操作推导出长方体、正方体的体积公式。(重点)
2. 应用长方体和正方体的体积计算公式解决实际问题。(难点)
学习目标
回顾复习
(1)物体所占空间的大小叫作物体的( )。
(2)计量体积要用体积单位,常用的体积单位有( )、( )和( ),
可以分别写成( )、( )和( ) 。
体积
立方厘米
立方分米
立方米
cm3
dm3
m3
1. 填一填。
回顾复习
2. 判断,并说明理由。
体积为1立方米的立体图形一定是棱长为1米的正方体。 ( )
×
理由:
据体积的意义,物体所占空间的大小叫做物体的体积。体积是1立方米的立体图形可能是正方体,也可能是长方体或其它形体。
(教材P29 例题)
探索新知
求长方体的体积就是看长方体有多少个体积单位。
把长方体分成若干单位体积的小正方体,就可以……
讨论一下:怎样计算长方体的体积?
探索新知
实验
用体积为 1 cm3的小正方体摆成不同的长方体。说一说你是怎么摆的。
②
①
③
④
探索新知
(1)把小组内摆法不同的长方体的相关数据填入下表。
长 宽 高 小正方体的数量 长方体的体积
12
1
1
12
12
4
3
1
12
12
6
2
1
12
12
3
2
2
12
12
探索新知
观察上表:摆出的长方体的体积与长、宽、高有什么关系?
长方体所含体积单位的个数就是长方体的体积。
长方体的体积正好等于长×宽×高的积。
探索新知
长方体的体积=长×宽×高
V=a b h
如果用字母V表示长方体的体积,用a,b,h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:
a
b
h
探索新知
根据长方体和正方体的关系,想一想正方体的体积怎样计算。
如果用字母V表示正方体的体积,用a表示它的棱长,那么正方体的体积计算公式可以写成:
V=a · a · a
a
探索新知
正方体的体积公式一般写成: V=a3
a·a·a也可以写作“a3”,读作“a的立方”,表示3个a相乘。
探索新知
1
(教材P30 例1)
保温箱的尺寸如下图所示,计算它们的体积。(单位:dm)
V=a b h
=6×5×4
=120(dm3)
V=a3
=53
=5×5×5
=125(dm3)
6
5
4
5
5
5
探索新知
长方体或正方体底面的面积叫做底面积。
底面
底面
长方体的体积=长×宽×高
底面积
正方体的体积=棱长×棱长×棱长
底面积
探索新知
所以,长方体和正方体的体积也可以这样来计算:
长方体(或正方体)的体积=底面积×高
如果用字母S表示底面积,上面的公式可以写成:
V=Sh
S
h
随堂小练
做一做
1. 一块长方体豆腐的尺寸如下图所示,它的体积是多少?
(教材P31做一做 第1题)
V=a b h
=15×7×5
=525(cm3)
答:它的体积是525 cm3。
随堂小练
做一做
2. 一根长方体木料,长5 m,横截面的面积是0.06 m2。这根木料的体积是多少 (教材P31做一做 第2题)
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06 m2
当堂检测
1. 填空。
(1)一个正方体的棱长为 5 cm,它的体积是
_________。
(2)一个长方体纸盒,长 6 dm,宽 5 dm,高
7 dm,它的体积是______dm3。
125cm3
210
当堂检测
30×30×30 = 27000(cm3)
答:它的体积是27000 cm3。
2. 一块棱长 30 cm 的正方体冰块,它的体积是多少
立方厘米?(教材P33练习七 第9题)
当堂检测
3. 家具厂订购500根方木,每根方木横截面的面
积是2.4 dm2,长是3 m。这些方木一共是多
少立方米 (教材P33练习七 第11题)
当堂检测
2.4 dm2=0.024 m2
0.024×3×500=36(m3)
36 m3=36(m3)
答:这些木料一共是36立方米。
当堂检测
4. 判断:
棱长是6 cm的正方体,体积和表面积相等。
( )
错解:√
当堂检测
错因分析:本题错在只看计算结果的数据,没看数据的单位。体积是216 cm3,表面积是216 cm2,两者表示的意义不同,不能比较。体积和表面积不是同类量,两者之间不能比较。
正解:×
学习完本节课,你有什么收获?
课堂小结
通过本节课的学习,我们掌握了长方体、正方体的体积公式。
课堂小结
课堂小结
长方体和正方体的体积公式:
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×棱长
V=a3
a
a
b
h
课堂小结
长方体和正方体体积的统一公式:
长方体(或正方体)的体积=底面积×高
V = Sh
S
h
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
