(2023春)人教版五年级数学下册 整理和复习(课件)(共22张PPT)
文档属性
| 名称 | (2023春)人教版五年级数学下册 整理和复习(课件)(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
2023春人教版 数学
五年级下册
3 长方体和正方体
整理和复习
1. 对长方体和正方体的特征、表面积和体积的含义、体积单位和容积单位以及
单位间的进率、表面积和体积的计算公式等知识进行梳理。(重点)
2. 通过合作交流和自主探索,学会在系统复习的基础上厘清知识网络,进行分
析归纳、逻辑推理,联系生活实际运用,提高自己的学习能力。(难点)
3. 对知识进行自我梳理,灵活运用知识解决实际问题。(难点)
学习目标
回顾复习
本单元学习了关于长方体和正方体的哪些知识?
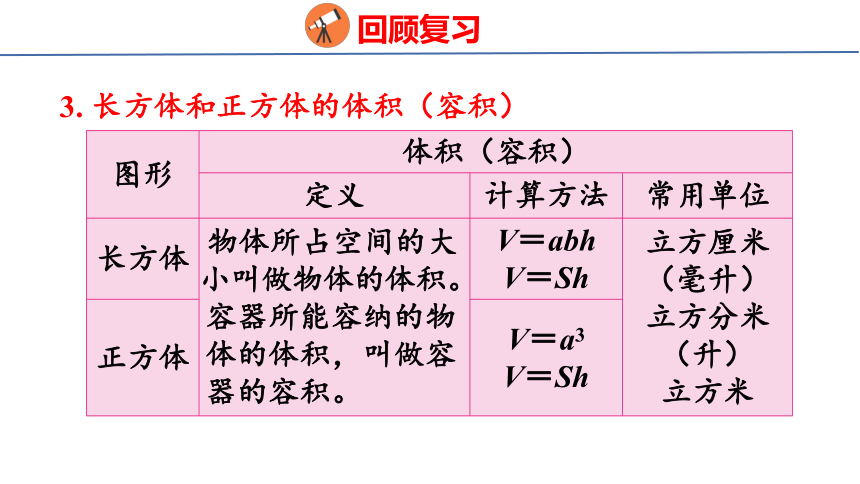
3. 长方体和正方体的体积(容积)
1. 长方体和正方体的认识
2. 长方体和正方体的表面积
回顾复习
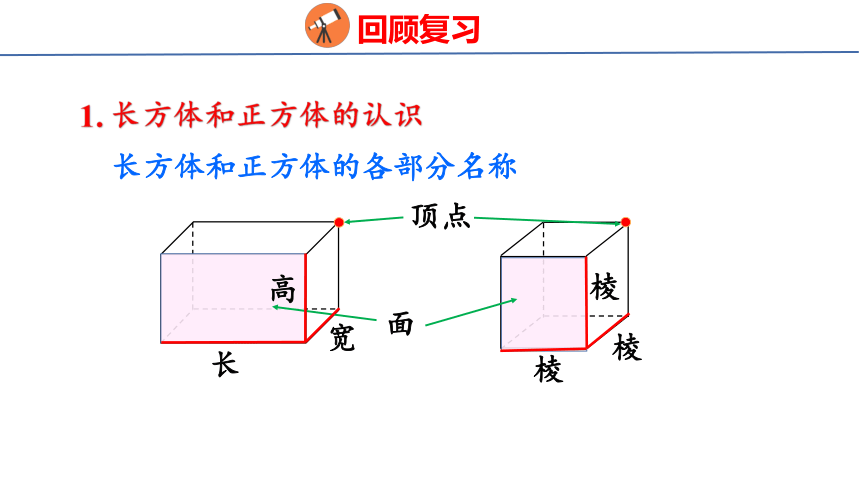
1. 长方体和正方体的认识
长方体和正方体的各部分名称
长
高
宽
棱
棱
棱
顶点
面
回顾复习
图形 相同点 不同点 联系
面 棱 顶点 面的形状 面的面积 棱长 正方体是特殊的长方体
长方体 6个 12条 8个 6个面都是长方形(特殊情况有2个面是正方形) 相对的面面积相等 相对的棱长度相等 正方体 6个面都是正方形 6个面的面积都相等 12条相等棱 长方体和正方体的特征
回顾复习
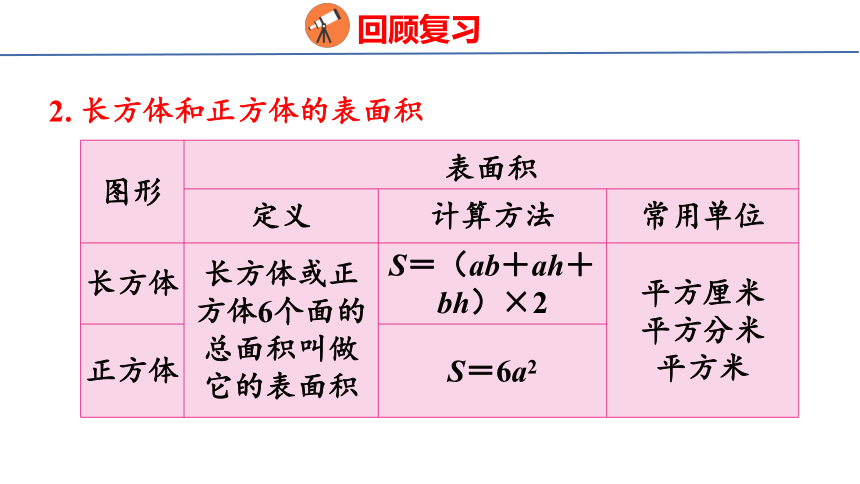
2. 长方体和正方体的表面积
图形 表面积 定义 计算方法 常用单位
长方体 长方体或正方体6个面的总面积叫做它的表面积 S=(ab+ah+bh)×2 平方厘米
平方分米
平方米
正方体 S=6a2 3. 长方体和正方体的体积(容积)
图形 体积(容积) 定义 计算方法 常用单位
长方体 物体所占空间的大 小叫做物体的体积。 容器所能容纳的物 体的体积,叫做容 器的容积。 V=abh V=Sh 立方厘米
(毫升)
立方分米
(升)
立方米
正方体 V=a3 V=Sh 回顾复习
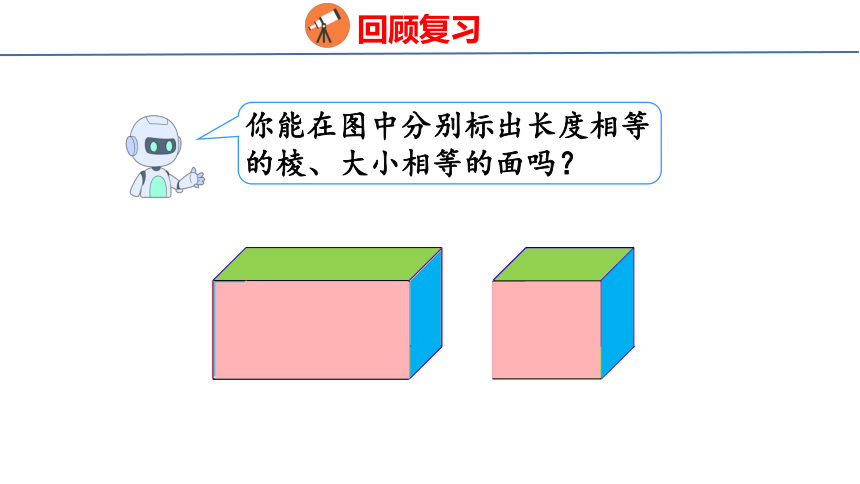
你能在图中分别标出长度相等的棱、大小相等的面吗?
回顾复习
1. 对照上图,完成下面的问题。
(1)用图示表示长方体和正方体的关系,并说
明为什么。
长方体
正方体
正方体是长、宽、高都相等的特殊长方体。
回顾复习
(2)在长方体中分别指出与红色线标示的棱平行
的棱和相交并垂直的棱,你能发现什么
1.长方体相对的棱平行且相等。
2.长、宽、高互相垂直。
回顾复习
(3)回忆计算表面积的方法以及探索体积公式
的过程,想一想关键是要知道什么?计算体积
与容积有什么相同点和不同点?
1. 关键是要知道长方体的长、宽、高;
2. 体积与容积计算方法一样,物体形状规则时,测量有关数据,利用公式计算;物体形状不规则时,想办法转化为规则的,常用“排水法”转化。
回顾复习
2. 你能用尺子和长方体(或正
方体)容器测出右面物体的
体积吗?如果用这种方法比
较两个物体体积的大小,你
打算怎么做?
回顾复习
玻璃球可以用“排水法”,转化为规则的。
绿豆也可以用“排水法”,但体积太小,水位上升不明显,可以多放一些绿豆在水中,如10粒、20粒,求出总体积后再除以10或20,得到每粒绿豆的体积。
回顾复习
随堂小练
做一做
下面的长方体都是用棱长 1 cm 的小正方体摆成的。计算它们的体积。
随堂小练
4cm
3cm
3×3×4=36(cm3)
4cm
4cm
4cm
4×4×4=64(cm3)
3cm
当堂检测
1. 下面是同一个长方体的展开图,说一说每个
图是怎样展开的。(教材P43 练习十 第1题)
上
左
右
前
后
下
上
右
前
后
下
左
当堂检测
找一些正方体纸盒并将其展开,你能展开成多少种不同的形状?
当堂检测
2. 长方体的长、宽、高都变为原来的2倍,它的表
面积和体积都发生了什么变化?(教材P43 练
习十 第2题)
长/cm 宽/cm 高/cm 表面积/cm2 体积/cm3
1 2 1 3
2 4 2 6
3 8 4 12
22
88
352
6
48
384
当堂检测
发现:
表面积变为原来的4倍,体积变为原来的8倍。
你发现了什么规律?
当堂检测
3. 一个长方体鱼塘长8 m,宽4.5 m,深2 m。
这个鱼塘的容积大约是多少?(教材P43 练
习十 第3题)
8×4.5×2=72(m )
答:这个鱼塘的容积大约是72 m 。
当堂检测
4. 某古建筑景点定做了25个宫灯(如右图,单位:cm)。宫灯外侧有一层外饰面(上、下面除外)。如果外饰面每平方米18元,这些宫灯的外饰面一共要花多少钱?(教材P43 练习十 第4题)
46×80×4+66×20×4=20000(cm )
答:这些宫灯的外饰面一共要花900元钱。
20000 cm =2 m
2×25×18=900(元)
2023春人教版 数学
五年级下册
3 长方体和正方体
整理和复习
1. 对长方体和正方体的特征、表面积和体积的含义、体积单位和容积单位以及
单位间的进率、表面积和体积的计算公式等知识进行梳理。(重点)
2. 通过合作交流和自主探索,学会在系统复习的基础上厘清知识网络,进行分
析归纳、逻辑推理,联系生活实际运用,提高自己的学习能力。(难点)
3. 对知识进行自我梳理,灵活运用知识解决实际问题。(难点)
学习目标
回顾复习
本单元学习了关于长方体和正方体的哪些知识?
3. 长方体和正方体的体积(容积)
1. 长方体和正方体的认识
2. 长方体和正方体的表面积
回顾复习
1. 长方体和正方体的认识
长方体和正方体的各部分名称
长
高
宽
棱
棱
棱
顶点
面
回顾复习
图形 相同点 不同点 联系
面 棱 顶点 面的形状 面的面积 棱长 正方体是特殊的长方体
长方体 6个 12条 8个 6个面都是长方形(特殊情况有2个面是正方形) 相对的面面积相等 相对的棱长度相等 正方体 6个面都是正方形 6个面的面积都相等 12条相等棱 长方体和正方体的特征
回顾复习
2. 长方体和正方体的表面积
图形 表面积 定义 计算方法 常用单位
长方体 长方体或正方体6个面的总面积叫做它的表面积 S=(ab+ah+bh)×2 平方厘米
平方分米
平方米
正方体 S=6a2 3. 长方体和正方体的体积(容积)
图形 体积(容积) 定义 计算方法 常用单位
长方体 物体所占空间的大 小叫做物体的体积。 容器所能容纳的物 体的体积,叫做容 器的容积。 V=abh V=Sh 立方厘米
(毫升)
立方分米
(升)
立方米
正方体 V=a3 V=Sh 回顾复习
你能在图中分别标出长度相等的棱、大小相等的面吗?
回顾复习
1. 对照上图,完成下面的问题。
(1)用图示表示长方体和正方体的关系,并说
明为什么。
长方体
正方体
正方体是长、宽、高都相等的特殊长方体。
回顾复习
(2)在长方体中分别指出与红色线标示的棱平行
的棱和相交并垂直的棱,你能发现什么
1.长方体相对的棱平行且相等。
2.长、宽、高互相垂直。
回顾复习
(3)回忆计算表面积的方法以及探索体积公式
的过程,想一想关键是要知道什么?计算体积
与容积有什么相同点和不同点?
1. 关键是要知道长方体的长、宽、高;
2. 体积与容积计算方法一样,物体形状规则时,测量有关数据,利用公式计算;物体形状不规则时,想办法转化为规则的,常用“排水法”转化。
回顾复习
2. 你能用尺子和长方体(或正
方体)容器测出右面物体的
体积吗?如果用这种方法比
较两个物体体积的大小,你
打算怎么做?
回顾复习
玻璃球可以用“排水法”,转化为规则的。
绿豆也可以用“排水法”,但体积太小,水位上升不明显,可以多放一些绿豆在水中,如10粒、20粒,求出总体积后再除以10或20,得到每粒绿豆的体积。
回顾复习
随堂小练
做一做
下面的长方体都是用棱长 1 cm 的小正方体摆成的。计算它们的体积。
随堂小练
4cm
3cm
3×3×4=36(cm3)
4cm
4cm
4cm
4×4×4=64(cm3)
3cm
当堂检测
1. 下面是同一个长方体的展开图,说一说每个
图是怎样展开的。(教材P43 练习十 第1题)
上
左
右
前
后
下
上
右
前
后
下
左
当堂检测
找一些正方体纸盒并将其展开,你能展开成多少种不同的形状?
当堂检测
2. 长方体的长、宽、高都变为原来的2倍,它的表
面积和体积都发生了什么变化?(教材P43 练
习十 第2题)
长/cm 宽/cm 高/cm 表面积/cm2 体积/cm3
1 2 1 3
2 4 2 6
3 8 4 12
22
88
352
6
48
384
当堂检测
发现:
表面积变为原来的4倍,体积变为原来的8倍。
你发现了什么规律?
当堂检测
3. 一个长方体鱼塘长8 m,宽4.5 m,深2 m。
这个鱼塘的容积大约是多少?(教材P43 练
习十 第3题)
8×4.5×2=72(m )
答:这个鱼塘的容积大约是72 m 。
当堂检测
4. 某古建筑景点定做了25个宫灯(如右图,单位:cm)。宫灯外侧有一层外饰面(上、下面除外)。如果外饰面每平方米18元,这些宫灯的外饰面一共要花多少钱?(教材P43 练习十 第4题)
46×80×4+66×20×4=20000(cm )
答:这些宫灯的外饰面一共要花900元钱。
20000 cm =2 m
2×25×18=900(元)
