人教A版数学选修4-4 1.1 平面直角坐标系(文科)课件(17张PPT)
文档属性
| 名称 | 人教A版数学选修4-4 1.1 平面直角坐标系(文科)课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 586.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 15:51:13 | ||
图片预览




文档简介
(共17张PPT)
第一讲 坐标系
1.平面直角坐标系
《选修4-4》
1..坐标法解决几何问题的“三部曲”:第一步,建立适当坐标系,用坐标和方程表示问题中涉及的 元素,将几何问题转化为 问题;第二步,通过代数运算解决代数问题;第三步:把代数运算结果翻译成 结论.
几何
代数
几何
知识点一 平面直角坐标系
探究
根据几何特点选择适当的直角坐标系的一些规则:
(1)如果图形有对称中心,可以选择对称中心为坐标原点;
(2)如果图形有对称轴,可以选择对称轴为坐标轴;
(3)使图形上的特殊点尽可能地在坐标轴上。
x
O
2
y=sinx
y=sin2x
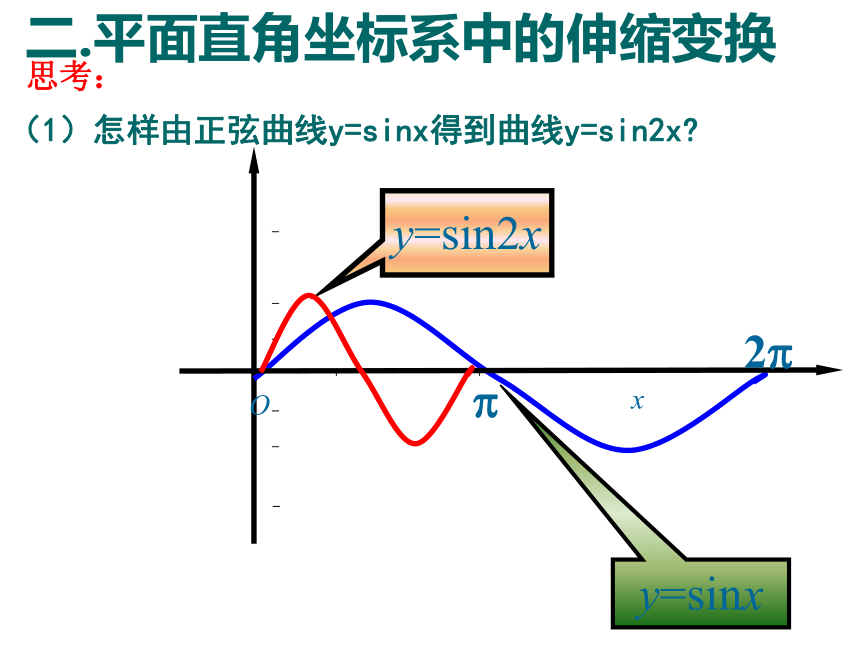
二.平面直角坐标系中的伸缩变换
思考:
(1)怎样由正弦曲线y=sinx得到曲线y=sin2x
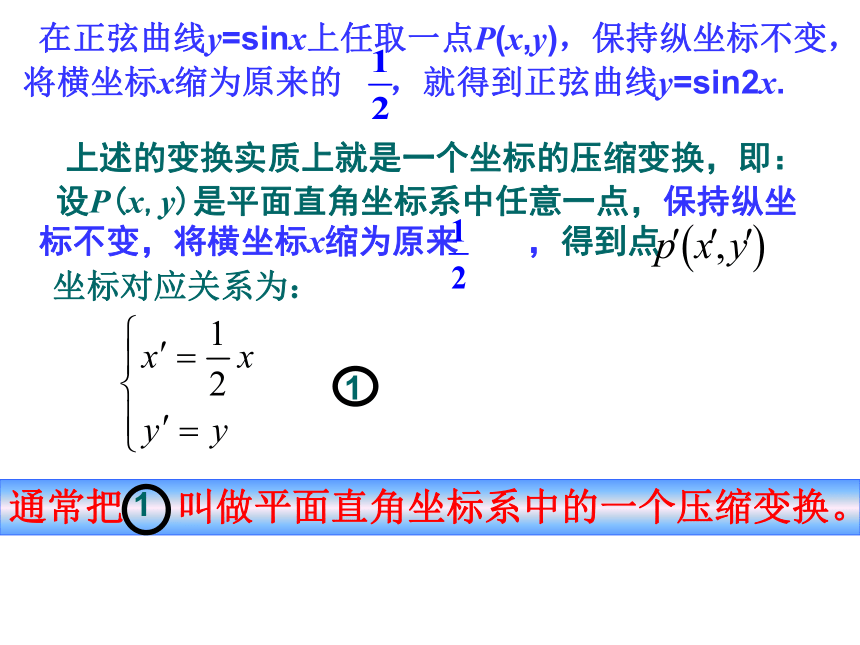
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的 ,就得到正弦曲线y=sin2x.
通常把 叫做平面直角坐标系中的一个压缩变换。
1
坐标对应关系为:
1
上述的变换实质上就是一个坐标的压缩变换,即:
设P(x,y)是平面直角坐标系中任意一点,保持纵坐标不变,将横坐标x缩为原来 ,得到点
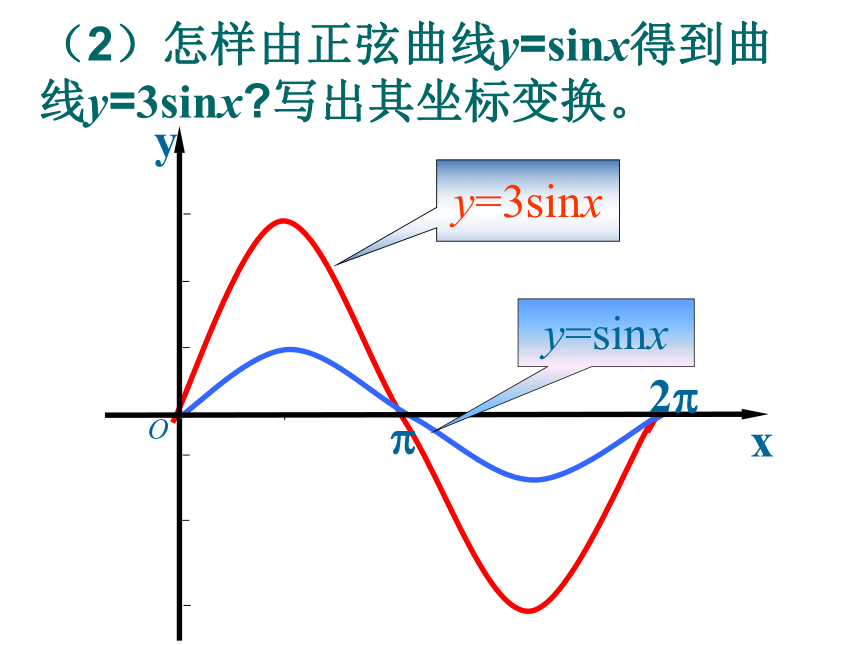
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx 写出其坐标变换。
O
2
y=sinx
y=3sinx
y
x
在正弦曲线上任取一点P(x,y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx 写出其坐标变换。
通常把 叫做平面直角坐标系中的一个坐标伸长变换。
2
2
设点P(x,y)经变换得到点为
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x 写出其坐标变换。
O
2
y=sinx
y=3sin2x
y
x
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的 ,在此基础上,将纵坐标变为原来的3倍,就得到正弦曲线y=3sin2x.
设点P(x,y)经变换得到点为
通常把 叫做平面直角坐标系中的一个坐标伸缩变换。
3
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x 写出其坐标变换。
3
知识点二 平面直角坐标系中的伸缩变换
平面直角坐标系中伸缩变换的定义
(1)平面直角坐标系中方程表示图形,那么平面图形的伸缩变换就可归结为_______伸缩变换,这就是用 研究 变换.
(2)平面直角坐标系中的坐标伸缩变换:设点P(x,y)是平面直角坐标系中任意一点,
在变换φ: 的作用下,点P(x,y)对应到点P′(x′,
y′),称 为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.
坐标的
代数方法
几何
φ
例2:在直角坐标系中,求下列方程所对应的图形经过伸缩变换
后的图形。
(1)2x+3y=0; (2)x2+y2=1
补例1 如图,圆O1与圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1,圆O2的切线PM,PN(M,N分别为切点),使得|PM|= |PN|,试建立适当的坐标系,并求动点P的轨迹方程.
一、坐标法
解 如图,以直线O1O2为x轴,线段O1O2的垂直平分线为y轴,建立平面直角坐标系,则O1(-2,0),O2(2,0).设P(x,y),
则|PM|2=|O1P|2-|O1M|2=(x+2)2+y2-1,
|PN|2=|O2P|2-|O2N|2=(x-2)2+y2-1.
∴(x+2)2+y2-1=2[(x-2)2+y2-1],
即x2-12x+y2+3=0,即(x-6)2+y2=33.
∴动点P的轨迹方程为(x-6)2+y2=33.
例1 如图,圆O1与圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1,圆O2的切线PM,PN(M,N分别为切点),使得|PM|= |PN|,试建立适当的坐标系,并求动点P的轨迹方程.
∴(x′,y′)满足x2+y2=1,即x′2+y′2=1.
2.B组作业:活页32-34页(12题除外)
课后作业
1.A组作业:活页32-34页全部
第一讲 坐标系
1.平面直角坐标系
《选修4-4》
1..坐标法解决几何问题的“三部曲”:第一步,建立适当坐标系,用坐标和方程表示问题中涉及的 元素,将几何问题转化为 问题;第二步,通过代数运算解决代数问题;第三步:把代数运算结果翻译成 结论.
几何
代数
几何
知识点一 平面直角坐标系
探究
根据几何特点选择适当的直角坐标系的一些规则:
(1)如果图形有对称中心,可以选择对称中心为坐标原点;
(2)如果图形有对称轴,可以选择对称轴为坐标轴;
(3)使图形上的特殊点尽可能地在坐标轴上。
x
O
2
y=sinx
y=sin2x
二.平面直角坐标系中的伸缩变换
思考:
(1)怎样由正弦曲线y=sinx得到曲线y=sin2x
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的 ,就得到正弦曲线y=sin2x.
通常把 叫做平面直角坐标系中的一个压缩变换。
1
坐标对应关系为:
1
上述的变换实质上就是一个坐标的压缩变换,即:
设P(x,y)是平面直角坐标系中任意一点,保持纵坐标不变,将横坐标x缩为原来 ,得到点
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx 写出其坐标变换。
O
2
y=sinx
y=3sinx
y
x
在正弦曲线上任取一点P(x,y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx 写出其坐标变换。
通常把 叫做平面直角坐标系中的一个坐标伸长变换。
2
2
设点P(x,y)经变换得到点为
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x 写出其坐标变换。
O
2
y=sinx
y=3sin2x
y
x
在正弦曲线y=sinx上任取一点P(x,y),保持纵坐标不变,将横坐标x缩为原来的 ,在此基础上,将纵坐标变为原来的3倍,就得到正弦曲线y=3sin2x.
设点P(x,y)经变换得到点为
通常把 叫做平面直角坐标系中的一个坐标伸缩变换。
3
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x 写出其坐标变换。
3
知识点二 平面直角坐标系中的伸缩变换
平面直角坐标系中伸缩变换的定义
(1)平面直角坐标系中方程表示图形,那么平面图形的伸缩变换就可归结为_______伸缩变换,这就是用 研究 变换.
(2)平面直角坐标系中的坐标伸缩变换:设点P(x,y)是平面直角坐标系中任意一点,
在变换φ: 的作用下,点P(x,y)对应到点P′(x′,
y′),称 为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.
坐标的
代数方法
几何
φ
例2:在直角坐标系中,求下列方程所对应的图形经过伸缩变换
后的图形。
(1)2x+3y=0; (2)x2+y2=1
补例1 如图,圆O1与圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1,圆O2的切线PM,PN(M,N分别为切点),使得|PM|= |PN|,试建立适当的坐标系,并求动点P的轨迹方程.
一、坐标法
解 如图,以直线O1O2为x轴,线段O1O2的垂直平分线为y轴,建立平面直角坐标系,则O1(-2,0),O2(2,0).设P(x,y),
则|PM|2=|O1P|2-|O1M|2=(x+2)2+y2-1,
|PN|2=|O2P|2-|O2N|2=(x-2)2+y2-1.
∴(x+2)2+y2-1=2[(x-2)2+y2-1],
即x2-12x+y2+3=0,即(x-6)2+y2=33.
∴动点P的轨迹方程为(x-6)2+y2=33.
例1 如图,圆O1与圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1,圆O2的切线PM,PN(M,N分别为切点),使得|PM|= |PN|,试建立适当的坐标系,并求动点P的轨迹方程.
∴(x′,y′)满足x2+y2=1,即x′2+y′2=1.
2.B组作业:活页32-34页(12题除外)
课后作业
1.A组作业:活页32-34页全部
