人教A版数学选修4-4 1.1.2 平面直角坐标系中的伸缩变换 课件(21张PPT)
文档属性
| 名称 | 人教A版数学选修4-4 1.1.2 平面直角坐标系中的伸缩变换 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 15:53:06 | ||
图片预览




文档简介
(共21张PPT)
缩
换
变
伸
3
1
2
探究新知
怎样由正弦曲线y=sinx得到曲线y=sin2x
怎样由正弦曲线y=sinx得到曲线y=3sinx
怎样由正弦曲线y=sinx得到曲线y=3sin2x
在三角函数图象的学习中,我们研究过下面的一些问题:
探究新知
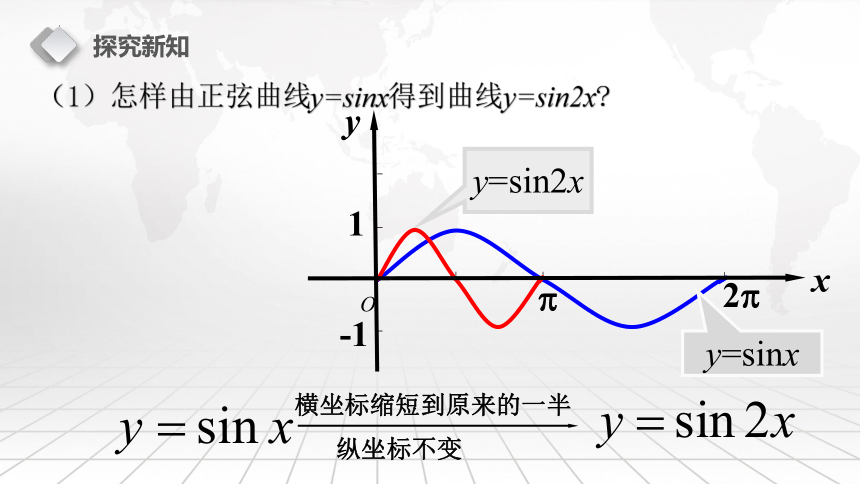
(1)怎样由正弦曲线y=sinx得到曲线y=sin2x
O
2
y=sinx
y=sin2x
y
x
横坐标缩短到原来的一半
纵坐标不变
1
-1
探究新知
O
2
y=sinx
y=sin2x
y
x
1
-1
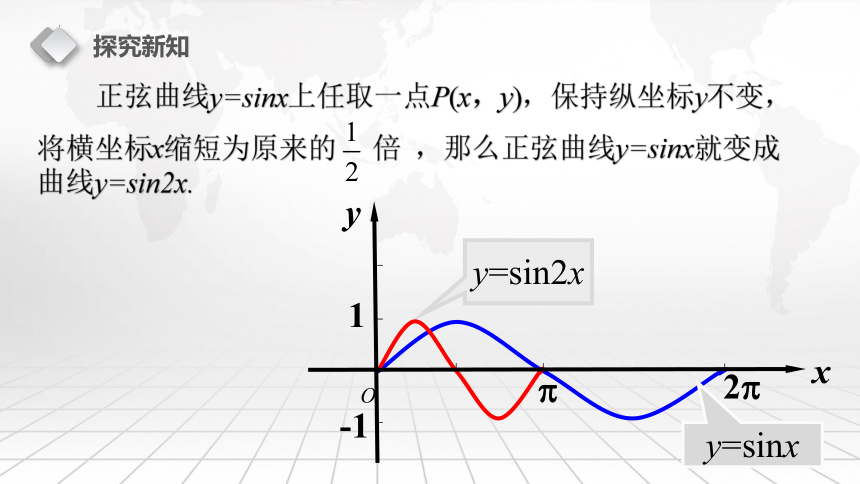
正弦曲线y=sinx上任取一点P(x,y),保持纵坐标y不变,
将横坐标x缩短为原来的 倍 ,那么正弦曲线y=sinx就变成曲线y=sin2x.
探究新知
从平面直角坐标系中的点的对应关系出发,你认为“保
持纵坐标y不变,将横坐标缩为原来的 ”的实质是什么?
实际上,“保持纵坐标y不变,将横坐标缩为原来的 ”
是一个纵坐标的压缩变换,即
设P(x,y)是平面直角坐标系中的任意一点,保持纵坐标
y不变,将横坐标缩为原来的 ,得到点 ,那么
我们把该式叫做平面直角坐标系中的一个坐标压
缩变换.
探究新知
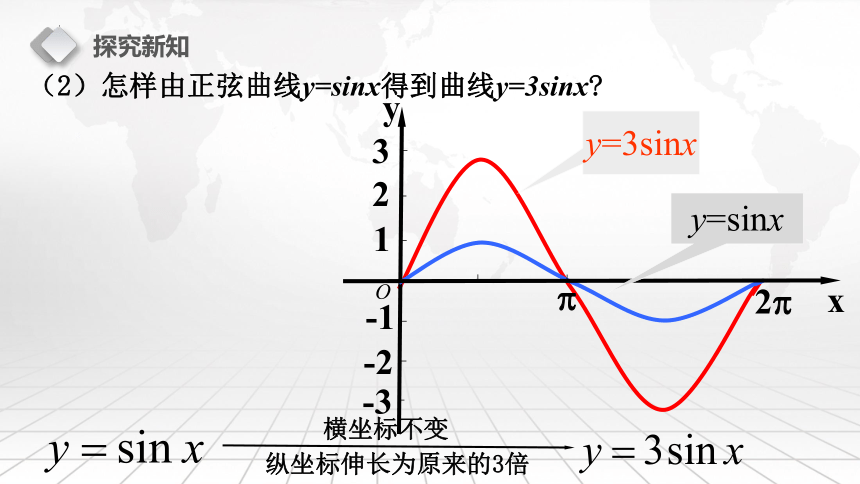
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx
O
2
y=sinx
y=3sinx
y
x
-1
1
2
3
-2
-3
横坐标不变
纵坐标伸长为原来的3倍
探究新知
O
2
y=sinx
y=3sinx
y
x
-1
1
2
3
-2
-3
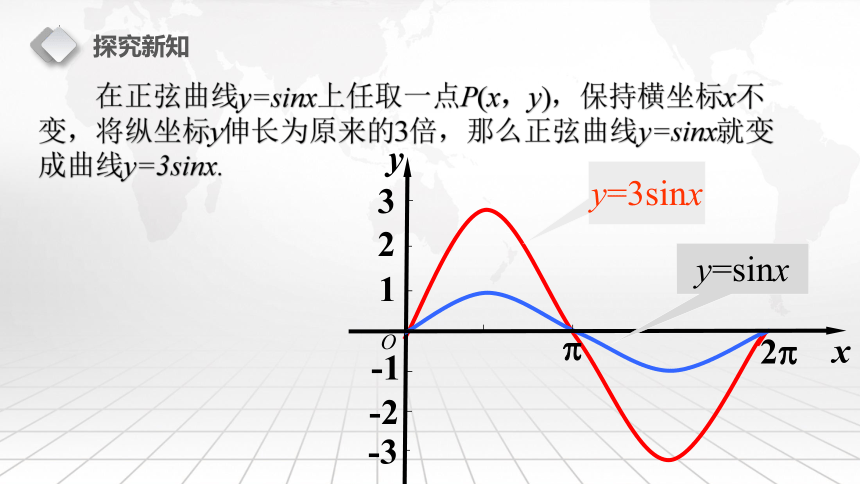
在正弦曲线y=sinx上任取一点P(x,y),保持横坐标x不变,将纵坐标y伸长为原来的3倍,那么正弦曲线y=sinx就变成曲线y=3sinx.
探究新知
从平面直角坐标系中的点的对应关系出发,你认为“保持横坐标x不变,将纵坐标y伸长为原来的3倍 ”的实质是什么?
实际上,“保持横坐标x不变,将纵坐标y伸长为原来的3倍 ”是一个坐标的伸长变换,即
设P(x,y)是平面直角坐标系中的任意一点,保持横坐标x不变,将纵坐标y伸长为原来的3倍,得到点 ,那么
我们把该式叫做平面直角坐标系中的一个坐标
伸长变换.
探究新知
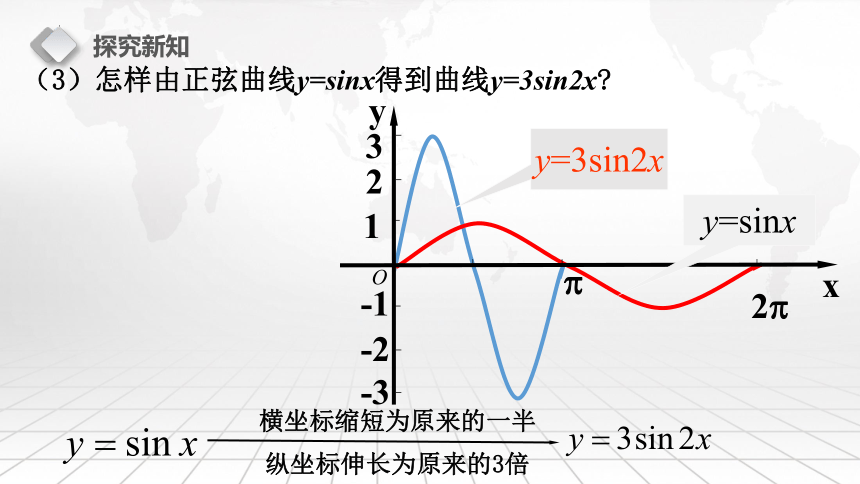
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x
O
2
y=sinx
y=3sin2x
y
x
-3
-2
-1
3
2
1
纵坐标伸长为原来的3倍
横坐标缩短为原来的一半
探究新知
设P(x,y)是平面直角坐标系中的任意一点,经过上述变换后变为点 ,那么
我们把该式叫做平面直角坐标系中的一个坐标
伸缩变换.
实际上,这是(1)(2)的“合成”,先保持纵坐标y不变,
将横坐标缩为原来的 ,在此基础上再保持横坐标x不变,
将纵坐标y伸长为原来的3倍 ”,就可以由正弦曲线y=sinx得到曲线y=3sin2x.
的作用下,点P(x,y)对应到点 ,称 为平面直角坐标系中的坐标伸缩变换。
、
设P(x,y)是平面直角坐标系中任意一点,在变换
伸缩变换
抽象定义
定 义
注 意
(1)
(2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
辨析定义
B
-4
2
(2,6)
(-4,-3)
抢答
在直角坐标系中,求下列方程所对应的图形经过伸缩变换
后的图形。
2
运用中提升
小试牛刀
在伸缩变换下,直线仍然变成直线,
而圆可以变成圆或椭圆。
在伸缩变换下,椭圆可以变成圆、
椭圆。
在伸缩变换下,抛物线变成抛物线,
双曲线变成双曲线。
归纳总结
学 有
所 获
01
变式
乘胜追击
答案:
答案:
02
反思中收获
凯旋归来话收获
对自己说,你有什么收获?
对老师说,你有什么疑惑?
对同学说,你有什么温馨提示?
1
2
1
一种工具:平面直角坐标系
一种解题方法:坐标法
两个思想:转化思想,数形结合思想
盘点收获
1
2
1
一种变换:坐标伸缩变换
一种探究方法:由特殊到一般(归纳法)
两个思想:转化思想,数形结合思想
盘点收获
02
D
达标检测
A
读书部分:阅读教材P9-P11书面作业:教材习题1.1:2、6(必做)课时分层作业(一)剩余部分挑战自我巩固中进步
缩
换
变
伸
3
1
2
探究新知
怎样由正弦曲线y=sinx得到曲线y=sin2x
怎样由正弦曲线y=sinx得到曲线y=3sinx
怎样由正弦曲线y=sinx得到曲线y=3sin2x
在三角函数图象的学习中,我们研究过下面的一些问题:
探究新知
(1)怎样由正弦曲线y=sinx得到曲线y=sin2x
O
2
y=sinx
y=sin2x
y
x
横坐标缩短到原来的一半
纵坐标不变
1
-1
探究新知
O
2
y=sinx
y=sin2x
y
x
1
-1
正弦曲线y=sinx上任取一点P(x,y),保持纵坐标y不变,
将横坐标x缩短为原来的 倍 ,那么正弦曲线y=sinx就变成曲线y=sin2x.
探究新知
从平面直角坐标系中的点的对应关系出发,你认为“保
持纵坐标y不变,将横坐标缩为原来的 ”的实质是什么?
实际上,“保持纵坐标y不变,将横坐标缩为原来的 ”
是一个纵坐标的压缩变换,即
设P(x,y)是平面直角坐标系中的任意一点,保持纵坐标
y不变,将横坐标缩为原来的 ,得到点 ,那么
我们把该式叫做平面直角坐标系中的一个坐标压
缩变换.
探究新知
(2)怎样由正弦曲线y=sinx得到曲线y=3sinx
O
2
y=sinx
y=3sinx
y
x
-1
1
2
3
-2
-3
横坐标不变
纵坐标伸长为原来的3倍
探究新知
O
2
y=sinx
y=3sinx
y
x
-1
1
2
3
-2
-3
在正弦曲线y=sinx上任取一点P(x,y),保持横坐标x不变,将纵坐标y伸长为原来的3倍,那么正弦曲线y=sinx就变成曲线y=3sinx.
探究新知
从平面直角坐标系中的点的对应关系出发,你认为“保持横坐标x不变,将纵坐标y伸长为原来的3倍 ”的实质是什么?
实际上,“保持横坐标x不变,将纵坐标y伸长为原来的3倍 ”是一个坐标的伸长变换,即
设P(x,y)是平面直角坐标系中的任意一点,保持横坐标x不变,将纵坐标y伸长为原来的3倍,得到点 ,那么
我们把该式叫做平面直角坐标系中的一个坐标
伸长变换.
探究新知
(3)怎样由正弦曲线y=sinx得到曲线y=3sin2x
O
2
y=sinx
y=3sin2x
y
x
-3
-2
-1
3
2
1
纵坐标伸长为原来的3倍
横坐标缩短为原来的一半
探究新知
设P(x,y)是平面直角坐标系中的任意一点,经过上述变换后变为点 ,那么
我们把该式叫做平面直角坐标系中的一个坐标
伸缩变换.
实际上,这是(1)(2)的“合成”,先保持纵坐标y不变,
将横坐标缩为原来的 ,在此基础上再保持横坐标x不变,
将纵坐标y伸长为原来的3倍 ”,就可以由正弦曲线y=sinx得到曲线y=3sin2x.
的作用下,点P(x,y)对应到点 ,称 为平面直角坐标系中的坐标伸缩变换。
、
设P(x,y)是平面直角坐标系中任意一点,在变换
伸缩变换
抽象定义
定 义
注 意
(1)
(2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;
(3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
辨析定义
B
-4
2
(2,6)
(-4,-3)
抢答
在直角坐标系中,求下列方程所对应的图形经过伸缩变换
后的图形。
2
运用中提升
小试牛刀
在伸缩变换下,直线仍然变成直线,
而圆可以变成圆或椭圆。
在伸缩变换下,椭圆可以变成圆、
椭圆。
在伸缩变换下,抛物线变成抛物线,
双曲线变成双曲线。
归纳总结
学 有
所 获
01
变式
乘胜追击
答案:
答案:
02
反思中收获
凯旋归来话收获
对自己说,你有什么收获?
对老师说,你有什么疑惑?
对同学说,你有什么温馨提示?
1
2
1
一种工具:平面直角坐标系
一种解题方法:坐标法
两个思想:转化思想,数形结合思想
盘点收获
1
2
1
一种变换:坐标伸缩变换
一种探究方法:由特殊到一般(归纳法)
两个思想:转化思想,数形结合思想
盘点收获
02
D
达标检测
A
读书部分:阅读教材P9-P11书面作业:教材习题1.1:2、6(必做)课时分层作业(一)剩余部分挑战自我巩固中进步
