人教A版数学选修4-4 1.3.1 圆的极坐标方程 课件(23张PPT)
文档属性
| 名称 | 人教A版数学选修4-4 1.3.1 圆的极坐标方程 课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 692.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 15:54:59 | ||
图片预览







文档简介
(共23张PPT)
的
坐
极
圆
标
方
程
1
2
教学目标
理解曲线的极坐标方程的概念.
认识几种圆的极坐标方程,比较它与直角坐标方程的异同.
3
掌握求圆的极坐标方程的方法.
重点
教学重点、难点
求圆的极坐标方程的方法与步骤.
难点
极坐标方程是涉及长度与角度的问题,列方程实质是解直角或斜三角形问题,要使用旧的三角知识.
复习回顾
θ
)
,
(
M
ρ
θ
极坐标与直角坐标的互化关系式:
设点M的直角坐标是(x,y),极坐标是(ρ,θ)
x=ρcosθ, y=ρsinθ
直角坐标化为极坐标:
极坐标化为直角坐标:
思考:极坐标如何化为直角坐标?
O
x
y
1
建立适当的
坐标系
2
3
4
限定点所满足
的条件
设点的坐标
代入坐标
进行运算
复习回顾
5
化简方程还原实际(查漏除杂)
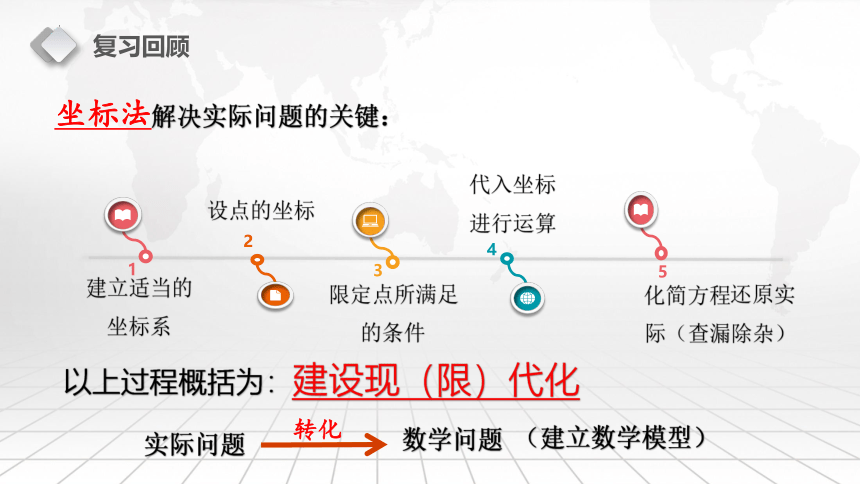
坐标法解决实际问题的关键:
以上过程概括为:建设现(限)代化
实际问题
数学问题
转化
(建立数学模型)
探究新知
热身训练:在平面直角坐标系中
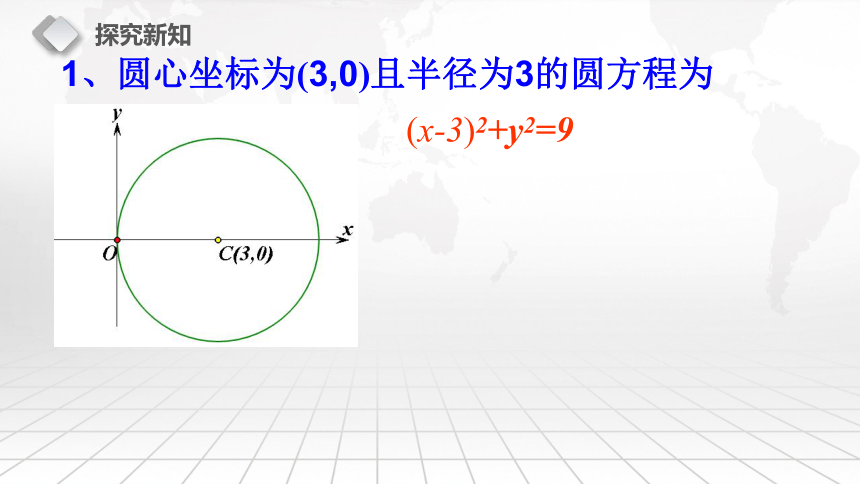
1、圆心坐标为(3,0)且半径为3的圆方程为
(x-3)2+y2=9
2、圆心坐标为(0,3)且半径为3的圆线方程为
x2+(y-3)2=9
x2+y2=9
3、圆心在原点半径为3的圆方程为_______
你能将以上三个方程化为极坐标方程?
思考:
新课引入
探究新知
求曲线的极坐标方程的步骤是什么?
与直角坐标系里的情况一样,求曲线的极坐标方程就是:
(1)建:根据题意建立恰当的坐标系;
(4)代:根据几何条件建立关于 , 的方程,并化简;
(2)设:点( , )是圆上任意一点;
(3)限:连接MO写出相应的限制条
(5)化:检验并确认所得的方程即为所求。
(x-3)2+y2=9
探究新知
1、圆心坐标为(3,0)且半径为3的圆方程为
P
A(6,0)
( , )
在△OPA中,易得│OP│=│OA│cos
即 =6cos
探究新知
1、圆心坐标为(3,0)且半径为3的圆方程为
思路分析:
1、建立极坐标系,作圆。
2、设点,并标出
3、找 的关系
4、对特殊点做检验化简得
5、下结论
P
A(6,0)
( , )
一般地,中心在C(a,0),半径为a的圆的极坐标方程为
=2acos
规范解答
1、圆心坐标为(3,0)且半径为3的圆方程为
一般地,在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程________________,并且坐标适合方程________________的点都在曲线C上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程.
曲线的极坐标方程
f( , )=0
f( , )=0
x2+(y-3)2=9
探究新知
2、圆心坐标为(0,3)且半径为3的圆的方程为
P
A(0,6)
( , )
在△OPA中,易得│OP│=│OA│cos( - )
即 =6sin
一般地,中心在C(0,a),半径为a的圆的极坐标方程为
=2asin
探究新知
2、圆心坐标为(0,3)且半径为3的圆线方程为
x2+y2=9
探究新知
3、圆心在原点半径为3的圆方程为_______
P
A(3,0)
( , )
在△OPA中,易得│OP│=
即 = 3
一般地,中心在极点,半径为r的圆的极坐标方程为
=r
探究新知
3、圆心在原点半径为3的圆方程为_______
直角坐标系 极坐标系 极坐标图形
1、圆心(3,0)半径为3 圆心(3,0)半径为3
2、圆心(0,3)半径为3 圆心(3, /2)
3、圆心(0,0)半径为3 圆心在极点,半径为3
(x-3)2+y2=9
x2+(y-3)2=9
x2+y2=9
=6cos
=6sin
=3
x
O
C(3, /2 )
x
O
3
C(3,0)
x
O
探究新知
中心在C( 0, 0 ),半径为r的圆的极坐标方程为
P( , )
r
0
( 0, 0 )
0
2+ 0 2 -2 0 cos( - 0)= r2
探究新知
归纳总结
(1)求曲线的极坐标方程与直角坐标系里的情况一样,就是找出动点M的坐标 与 之间的关系,然后列出方程f ( , )=0,再化简并检验特殊点.
(2)极坐标方程涉及的是长度与角度,因此列方程的实质是解直角三角形或斜三角形.
典型例题
A
解:依题意知,该圆过极点O,设直线OA交该圆于点M,点P(ρ, θ )是圆上异于O、M的任意一点,连结OP,PM。
O
x
M
P(ρ, θ )
经检验可知,这两点的坐标都满足上式
在Rt△OPM中,
∴所求圆的极坐标方程为
典型例题
解法2:以极点为原点,极轴所在直线为x轴建立直角坐标系,设点A的直角坐标为(a,b),则
典型例题
【例2】把下列极坐标方程化成直角坐标方程。
读书部分:阅读教材P12-P14书面作业:点金训练剩余部分课时分层作业(二)剩余部分挑战自我巩固中进步
的
坐
极
圆
标
方
程
1
2
教学目标
理解曲线的极坐标方程的概念.
认识几种圆的极坐标方程,比较它与直角坐标方程的异同.
3
掌握求圆的极坐标方程的方法.
重点
教学重点、难点
求圆的极坐标方程的方法与步骤.
难点
极坐标方程是涉及长度与角度的问题,列方程实质是解直角或斜三角形问题,要使用旧的三角知识.
复习回顾
θ
)
,
(
M
ρ
θ
极坐标与直角坐标的互化关系式:
设点M的直角坐标是(x,y),极坐标是(ρ,θ)
x=ρcosθ, y=ρsinθ
直角坐标化为极坐标:
极坐标化为直角坐标:
思考:极坐标如何化为直角坐标?
O
x
y
1
建立适当的
坐标系
2
3
4
限定点所满足
的条件
设点的坐标
代入坐标
进行运算
复习回顾
5
化简方程还原实际(查漏除杂)
坐标法解决实际问题的关键:
以上过程概括为:建设现(限)代化
实际问题
数学问题
转化
(建立数学模型)
探究新知
热身训练:在平面直角坐标系中
1、圆心坐标为(3,0)且半径为3的圆方程为
(x-3)2+y2=9
2、圆心坐标为(0,3)且半径为3的圆线方程为
x2+(y-3)2=9
x2+y2=9
3、圆心在原点半径为3的圆方程为_______
你能将以上三个方程化为极坐标方程?
思考:
新课引入
探究新知
求曲线的极坐标方程的步骤是什么?
与直角坐标系里的情况一样,求曲线的极坐标方程就是:
(1)建:根据题意建立恰当的坐标系;
(4)代:根据几何条件建立关于 , 的方程,并化简;
(2)设:点( , )是圆上任意一点;
(3)限:连接MO写出相应的限制条
(5)化:检验并确认所得的方程即为所求。
(x-3)2+y2=9
探究新知
1、圆心坐标为(3,0)且半径为3的圆方程为
P
A(6,0)
( , )
在△OPA中,易得│OP│=│OA│cos
即 =6cos
探究新知
1、圆心坐标为(3,0)且半径为3的圆方程为
思路分析:
1、建立极坐标系,作圆。
2、设点,并标出
3、找 的关系
4、对特殊点做检验化简得
5、下结论
P
A(6,0)
( , )
一般地,中心在C(a,0),半径为a的圆的极坐标方程为
=2acos
规范解答
1、圆心坐标为(3,0)且半径为3的圆方程为
一般地,在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程________________,并且坐标适合方程________________的点都在曲线C上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程.
曲线的极坐标方程
f( , )=0
f( , )=0
x2+(y-3)2=9
探究新知
2、圆心坐标为(0,3)且半径为3的圆的方程为
P
A(0,6)
( , )
在△OPA中,易得│OP│=│OA│cos( - )
即 =6sin
一般地,中心在C(0,a),半径为a的圆的极坐标方程为
=2asin
探究新知
2、圆心坐标为(0,3)且半径为3的圆线方程为
x2+y2=9
探究新知
3、圆心在原点半径为3的圆方程为_______
P
A(3,0)
( , )
在△OPA中,易得│OP│=
即 = 3
一般地,中心在极点,半径为r的圆的极坐标方程为
=r
探究新知
3、圆心在原点半径为3的圆方程为_______
直角坐标系 极坐标系 极坐标图形
1、圆心(3,0)半径为3 圆心(3,0)半径为3
2、圆心(0,3)半径为3 圆心(3, /2)
3、圆心(0,0)半径为3 圆心在极点,半径为3
(x-3)2+y2=9
x2+(y-3)2=9
x2+y2=9
=6cos
=6sin
=3
x
O
C(3, /2 )
x
O
3
C(3,0)
x
O
探究新知
中心在C( 0, 0 ),半径为r的圆的极坐标方程为
P( , )
r
0
( 0, 0 )
0
2+ 0 2 -2 0 cos( - 0)= r2
探究新知
归纳总结
(1)求曲线的极坐标方程与直角坐标系里的情况一样,就是找出动点M的坐标 与 之间的关系,然后列出方程f ( , )=0,再化简并检验特殊点.
(2)极坐标方程涉及的是长度与角度,因此列方程的实质是解直角三角形或斜三角形.
典型例题
A
解:依题意知,该圆过极点O,设直线OA交该圆于点M,点P(ρ, θ )是圆上异于O、M的任意一点,连结OP,PM。
O
x
M
P(ρ, θ )
经检验可知,这两点的坐标都满足上式
在Rt△OPM中,
∴所求圆的极坐标方程为
典型例题
解法2:以极点为原点,极轴所在直线为x轴建立直角坐标系,设点A的直角坐标为(a,b),则
典型例题
【例2】把下列极坐标方程化成直角坐标方程。
读书部分:阅读教材P12-P14书面作业:点金训练剩余部分课时分层作业(二)剩余部分挑战自我巩固中进步
