1.2.1 极坐标系的概念 课件-2022-2023学年高二数学(文)人教A版选修4-4 课件(30张PPT)
文档属性
| 名称 | 1.2.1 极坐标系的概念 课件-2022-2023学年高二数学(文)人教A版选修4-4 课件(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 916.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
第一讲 坐标系
1.2.1极坐标系的概念
《选修4-4》
平面直角坐标系内的点P与其坐标(a,b)一一对应
P
.
x
y
O
平面直角坐标系
a
b
(a,b)
平面直角坐标系是最简单最常用的一种坐标系,但不是唯一的一种坐标系.有时用别的坐标系比较方便.
还有什么坐标系呢
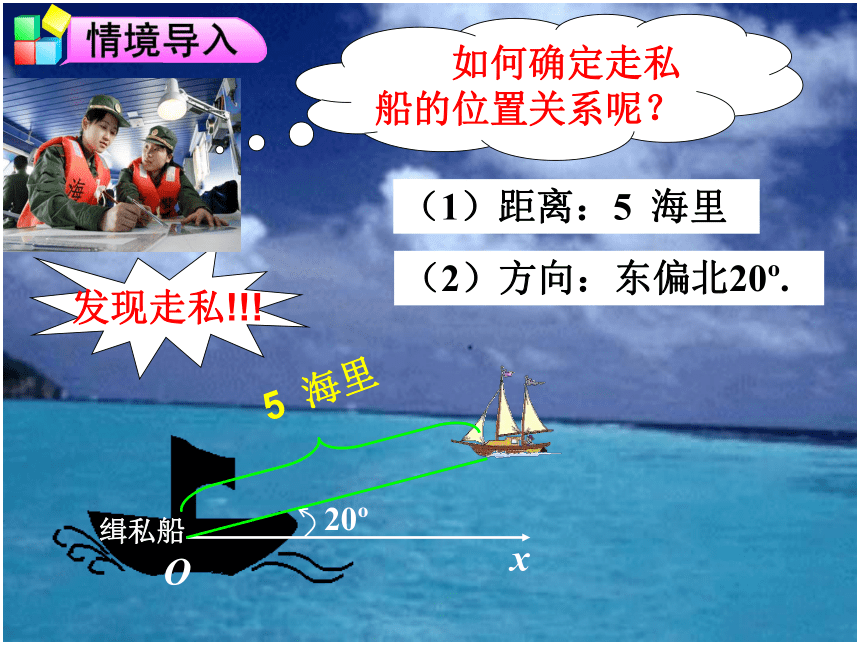
5 海里
(1)距离:5 海里
(2)方向:东偏北20 .
O
x
缉私船
20
发现走私!!!
如何确定走私船的位置关系呢?
45o
60m
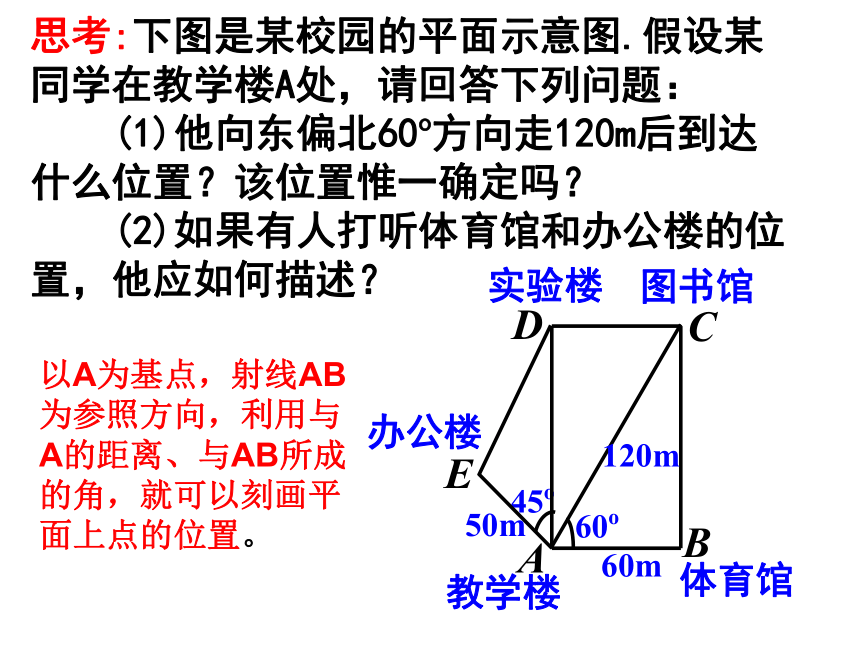
思考:下图是某校园的平面示意图.假设某
同学在教学楼A处,请回答下列问题:
(1)他向东偏北60o方向走120m后到达
什么位置?该位置惟一确定吗?
(2)如果有人打听体育馆和办公楼的位
置,他应如何描述?
A
E
B
C
D
60o
办公楼
实验楼
图书馆
体育馆
120m
教学楼
50m
以A为基点,射线AB为参照方向,利用与A的距离、与AB所成的角,就可以刻画平面上点的位置。
可以用方向和距离来表示一点的位置
这种用方向和距离表示平面内一点的位置的思想,就是极坐标的基本思想。
阅读教材:P8---11
思考下列问题:
什么是极坐标系
极坐标系中的点与坐标有何关系
直角坐标与极坐标如何互化
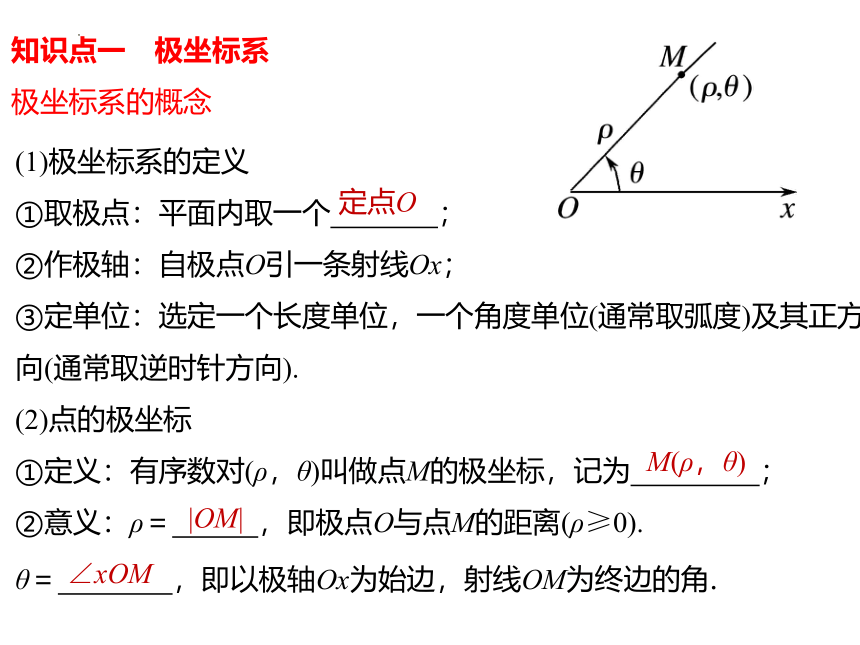
知识点一 极坐标系
极坐标系的概念
(1)极坐标系的定义
①取极点:平面内取一个 ;
②作极轴:自极点O引一条射线Ox;
③定单位:选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向).
(2)点的极坐标
①定义:有序数对(ρ,θ)叫做点M的极坐标,记为 ;
②意义:ρ= ,即极点O与点M的距离(ρ≥0).
θ= ,即以极轴Ox为始边,射线OM为终边的角.
定点O
M(ρ,θ)
|OM|
∠xOM
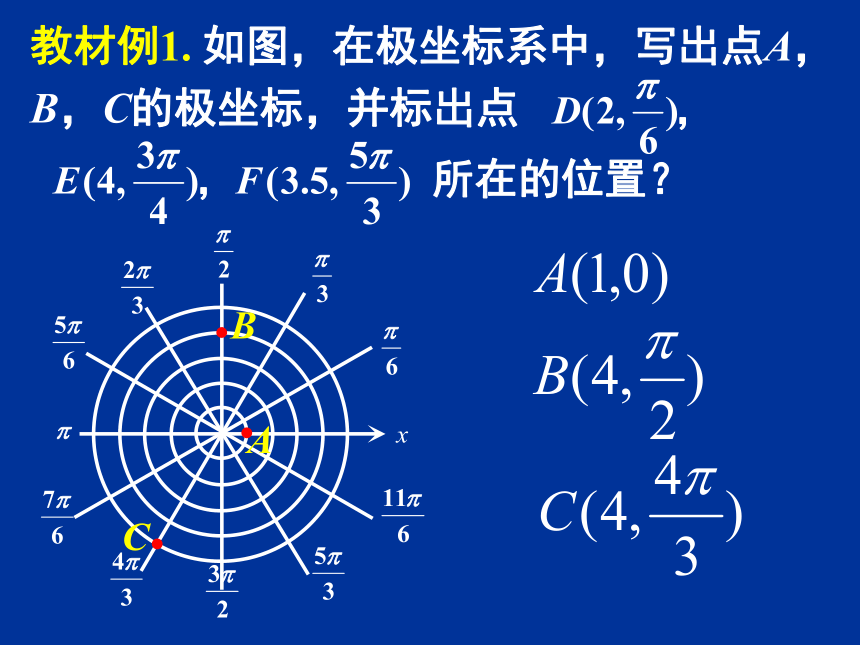
教材例1. 如图,在极坐标系中,写出点A,
B,C的极坐标,并标出点
所在的位置?
教材例1. 如图,在极坐标系中,写出点A,
B,C的极坐标,并标出点
所在的位置?
解:如图,以点A为极点,AB所在的射线为极轴,建立极坐标系.
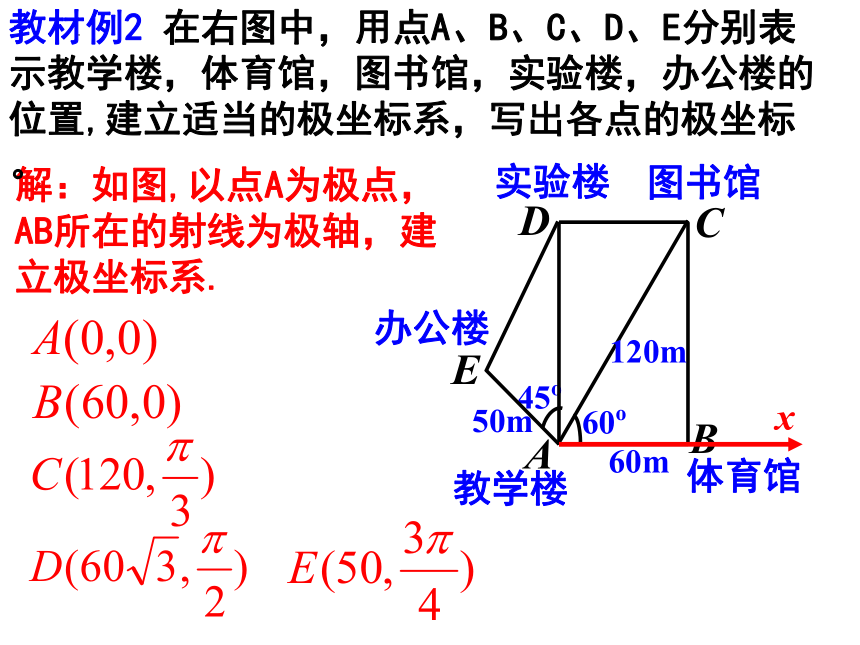
教材例2 在右图中,用点A、B、C、D、E分别表示教学楼,体育馆,图书馆,实验楼,办公楼的位置,建立适当的极坐标系,写出各点的极坐标。
45o
60m
A
E
B
C
D
60o
办公楼
实验楼
图书馆
体育馆
120m
教学楼
50m
x
在同一极坐标系中,有如下极坐标:
(1)这些极坐标之间有何异同?
(2)这些极角有何关系?
(3)这些极坐标所表示的点有什么关系
极径相同,极角不同
极角的始边相同,终边也相同,
即:它们是终边相同的角
它们表示同一个点
思考
①平面内一个点的极坐标是否唯一?
②若不唯一,那有多少种表示方法?
③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式?
思考
极坐标系下点与它的极坐标的对应情况
(1)给定一个( , ),就可以在坐标平面内确定惟一的点M
(2)给定平面上一点M,却有无数个极坐标与之对应
若规定 > 0, 0≤ <2π, 则除极点外,平面内的点与其极坐标一一对应
补例1 根据下列极坐标,作出各点.
解 在极坐标系中,点A,B,C,D的位置是确定的.
题型一 极坐标的表示
补例2:在极坐标系中,点A的极坐标是 ,
(规定: >0,0≤θ<2π)则
(1)点A关于极轴对称的点的极坐标是______
(2)点A关于极点对称的点的极坐标是_____
(3)点A关于过极点且与极轴垂直的直线对称
的点的极坐标是_____
题型二 极坐标系中求点的坐标和对称性
知识点二 极坐标和直角坐标的互化
(2)互化公式
①极坐标化直角坐标:
②直角坐标化极坐标:
(1)互化的前提条件:①极坐标系中的极点与直角坐标系中的原点重合②极轴与x轴的正半轴重合③两种坐标系取相同的长度单位.
ρcos θ
ρsin θ
x2+y2
解:
所以, 点M的直角坐标为
教材例3. 将点M的极坐标 化成直角坐标.
题型三 直角坐标与极坐标互化
教材例4. 将点M的直角坐标 化成极坐标.
解:
因为点在第三象限, 所以 ,
因此, 点M的极坐标为 。
∴△AOB为直角三角形,
(2)求AB的中点的极坐标.
解 取AB的中点M,连接OM,
(2)求AB的中点的极坐标.
有序数对( , )就叫做M的极坐标。
记作M( , )
1.点的极坐标
设M是平面内一点,极点O与点M的距离|OM|叫做点M的极径,记作 ;以极轴Ox为始边,射线OM为终边的角xOM叫做点M的极角,记作
x
O
M
2.极坐标系下点与它的极坐标的对应情况
(1)给定一个( , ),就可以在坐标平面内确定惟一的点M
(2)给定平面上一点M,却有无数个极坐标与之对应
极坐标 与
表示同一个点
3.极坐标与直角坐标的互化公式
②
①
极坐标化直角坐标用公式①
直角坐标化极坐标用公式②
注意:互化条件
x
O
y
α的终边
P(x,y)
r
2.B组作业:活页35-37页
课后作业
1.A组作业:活页35-37页
大书备选例题例1,例2
补充:负极径的定义
说明:一般情况下,极径都是正值;在某些必要情况下,极径也可以取负值。
对于点M(- , )( >0) ,规定:
(1)作射线OP,使 xOP=
(2)在OP的反向延长线上取一点M,使 OM =
O
x
P
M
(- , )
负极径的实质
从比较来看,负极径比正极径多了一个操作,将射线OP“反向延长”。
O
X
P
M
O
X
P
M
而反向延长也可以看成是旋转 ,因此,所谓“负极径”实质是管方向的。这与数学中通常的习惯一致,用“负”表示“反向 ”。
极坐标系下点的极坐标
O
x
P
M
⑴极径是正的时候:
⑵极径是负的时候:
第一讲 坐标系
1.2.1极坐标系的概念
《选修4-4》
平面直角坐标系内的点P与其坐标(a,b)一一对应
P
.
x
y
O
平面直角坐标系
a
b
(a,b)
平面直角坐标系是最简单最常用的一种坐标系,但不是唯一的一种坐标系.有时用别的坐标系比较方便.
还有什么坐标系呢
5 海里
(1)距离:5 海里
(2)方向:东偏北20 .
O
x
缉私船
20
发现走私!!!
如何确定走私船的位置关系呢?
45o
60m
思考:下图是某校园的平面示意图.假设某
同学在教学楼A处,请回答下列问题:
(1)他向东偏北60o方向走120m后到达
什么位置?该位置惟一确定吗?
(2)如果有人打听体育馆和办公楼的位
置,他应如何描述?
A
E
B
C
D
60o
办公楼
实验楼
图书馆
体育馆
120m
教学楼
50m
以A为基点,射线AB为参照方向,利用与A的距离、与AB所成的角,就可以刻画平面上点的位置。
可以用方向和距离来表示一点的位置
这种用方向和距离表示平面内一点的位置的思想,就是极坐标的基本思想。
阅读教材:P8---11
思考下列问题:
什么是极坐标系
极坐标系中的点与坐标有何关系
直角坐标与极坐标如何互化
知识点一 极坐标系
极坐标系的概念
(1)极坐标系的定义
①取极点:平面内取一个 ;
②作极轴:自极点O引一条射线Ox;
③定单位:选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向).
(2)点的极坐标
①定义:有序数对(ρ,θ)叫做点M的极坐标,记为 ;
②意义:ρ= ,即极点O与点M的距离(ρ≥0).
θ= ,即以极轴Ox为始边,射线OM为终边的角.
定点O
M(ρ,θ)
|OM|
∠xOM
教材例1. 如图,在极坐标系中,写出点A,
B,C的极坐标,并标出点
所在的位置?
教材例1. 如图,在极坐标系中,写出点A,
B,C的极坐标,并标出点
所在的位置?
解:如图,以点A为极点,AB所在的射线为极轴,建立极坐标系.
教材例2 在右图中,用点A、B、C、D、E分别表示教学楼,体育馆,图书馆,实验楼,办公楼的位置,建立适当的极坐标系,写出各点的极坐标。
45o
60m
A
E
B
C
D
60o
办公楼
实验楼
图书馆
体育馆
120m
教学楼
50m
x
在同一极坐标系中,有如下极坐标:
(1)这些极坐标之间有何异同?
(2)这些极角有何关系?
(3)这些极坐标所表示的点有什么关系
极径相同,极角不同
极角的始边相同,终边也相同,
即:它们是终边相同的角
它们表示同一个点
思考
①平面内一个点的极坐标是否唯一?
②若不唯一,那有多少种表示方法?
③坐标不唯一是由谁引起的?
④不同的极坐标是否可以写出统一表达式?
思考
极坐标系下点与它的极坐标的对应情况
(1)给定一个( , ),就可以在坐标平面内确定惟一的点M
(2)给定平面上一点M,却有无数个极坐标与之对应
若规定 > 0, 0≤ <2π, 则除极点外,平面内的点与其极坐标一一对应
补例1 根据下列极坐标,作出各点.
解 在极坐标系中,点A,B,C,D的位置是确定的.
题型一 极坐标的表示
补例2:在极坐标系中,点A的极坐标是 ,
(规定: >0,0≤θ<2π)则
(1)点A关于极轴对称的点的极坐标是______
(2)点A关于极点对称的点的极坐标是_____
(3)点A关于过极点且与极轴垂直的直线对称
的点的极坐标是_____
题型二 极坐标系中求点的坐标和对称性
知识点二 极坐标和直角坐标的互化
(2)互化公式
①极坐标化直角坐标:
②直角坐标化极坐标:
(1)互化的前提条件:①极坐标系中的极点与直角坐标系中的原点重合②极轴与x轴的正半轴重合③两种坐标系取相同的长度单位.
ρcos θ
ρsin θ
x2+y2
解:
所以, 点M的直角坐标为
教材例3. 将点M的极坐标 化成直角坐标.
题型三 直角坐标与极坐标互化
教材例4. 将点M的直角坐标 化成极坐标.
解:
因为点在第三象限, 所以 ,
因此, 点M的极坐标为 。
∴△AOB为直角三角形,
(2)求AB的中点的极坐标.
解 取AB的中点M,连接OM,
(2)求AB的中点的极坐标.
有序数对( , )就叫做M的极坐标。
记作M( , )
1.点的极坐标
设M是平面内一点,极点O与点M的距离|OM|叫做点M的极径,记作 ;以极轴Ox为始边,射线OM为终边的角xOM叫做点M的极角,记作
x
O
M
2.极坐标系下点与它的极坐标的对应情况
(1)给定一个( , ),就可以在坐标平面内确定惟一的点M
(2)给定平面上一点M,却有无数个极坐标与之对应
极坐标 与
表示同一个点
3.极坐标与直角坐标的互化公式
②
①
极坐标化直角坐标用公式①
直角坐标化极坐标用公式②
注意:互化条件
x
O
y
α的终边
P(x,y)
r
2.B组作业:活页35-37页
课后作业
1.A组作业:活页35-37页
大书备选例题例1,例2
补充:负极径的定义
说明:一般情况下,极径都是正值;在某些必要情况下,极径也可以取负值。
对于点M(- , )( >0) ,规定:
(1)作射线OP,使 xOP=
(2)在OP的反向延长线上取一点M,使 OM =
O
x
P
M
(- , )
负极径的实质
从比较来看,负极径比正极径多了一个操作,将射线OP“反向延长”。
O
X
P
M
O
X
P
M
而反向延长也可以看成是旋转 ,因此,所谓“负极径”实质是管方向的。这与数学中通常的习惯一致,用“负”表示“反向 ”。
极坐标系下点的极坐标
O
x
P
M
⑴极径是正的时候:
⑵极径是负的时候:
