(2023春)人教版五年级数学下册 第1课时 数与代数(课件)(共23张PPT)
文档属性
| 名称 | (2023春)人教版五年级数学下册 第1课时 数与代数(课件)(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 10:48:20 | ||
图片预览








文档简介
(共23张PPT)
2023春人教版 数学
五年级下册
9 总复习
9.1 数与代数
1. 理解因数和倍数的意义,并能利用因数和倍数的知识解决实际问题。(重点)
2. 掌握分数的意义及其性质,并能进行分数的加法和减法。(难点)
学习目标
回顾复习
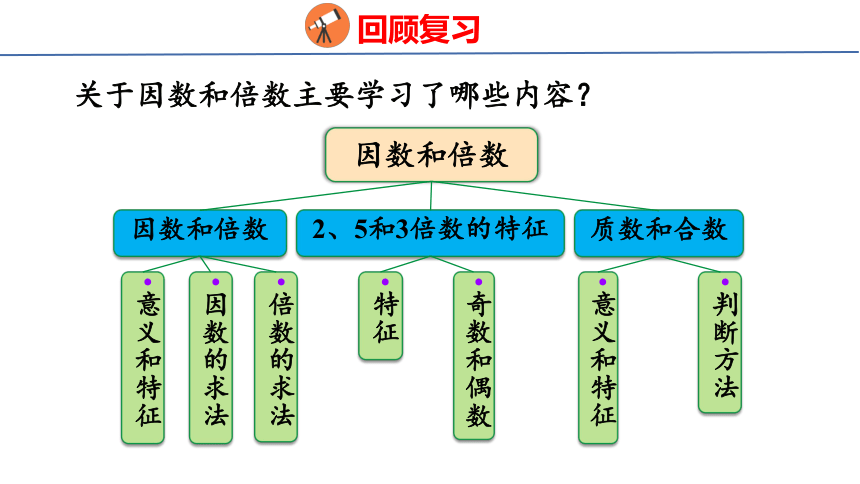
关于因数和倍数主要学习了哪些内容?
因数和倍数
因数和倍数
意义和特征
特征
2、5和3倍数的特征
奇数和偶数
倍数的求法
质数和合数
因数的求法
意义和特征
判断方法
回顾复习
1. 因数和倍数
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。
回顾复习
2. 公因数和公倍数
几个数公有的倍数叫作它们的公倍数,其中最小的一个叫作它们的最小公倍数,没有最大的公倍数;几个数公有的因数叫作它们的公因数,最小的公因数是1,最大的公因数叫作它们的最大公因数。
回顾复习
3. 2、5、3的倍数的特征
个位上是0,2,4,6,8的数都是2的倍数。
一个数各位上的数的和是3的倍数就是3的倍数。
个位上是0、5的数都是5的倍数。
整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数。
4. 奇数和偶数
回顾复习
5. 质数和合数
一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数);一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。1既不是质数,也不是合数。
公因数只有1的两个数,叫作互质数。
6. 互质数
回顾复习
7. 最大公因数和最小公倍数
几个数公有的因数,叫作它们的公因数,其中最大的公因数,叫作它们的最大公因数。几个数公有的倍数,叫作它们的公倍数,其中最小的公倍数,叫作它们的最小公倍数。求最大公因数和最小公倍数常用的方法有:列举法、筛选法、分解质因数法和短除法。
回顾复习
关于分数主要学习了哪些内容?
分数
意义
分数的意义
分数的基本性质
性质
约分与通分
真分数和假分数
加减法
分数与除法
同分母分数加减法
异分母分数加减法
分数与小数的互化
回顾复习
1. 分数的意义
一个或一些物体都可以看作一个整体,用自然数 1 来表示,通常把它叫作单位“1”。把单位“1”平均分成若干份,表示其中一份的数叫作分数单位。
回顾复习
2. 分数与除法的关系
分数与除法的关系:被除数÷除数= 。
分子比分母小的分数叫作真分数。真分数小于1。分子比分母大或者分子和分母相等的分数,叫作假分数。假分数等于或大于1。由整数(不包括0)和真分数合成的数,通常叫作带分数。
3. 真分数和假分数
回顾复习
4. 约分和通分
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。
依据:分数的基本性质
把一个分数化成和它相等,但分子分母都比较小的分数,叫作约分。把异分母分数分别化成和原来分数相等的同分母分数,叫作通分。
回顾复习
5. 分数和小数的互化
小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数点去掉作分子。能约分的要约分。分数化成小数:要用分子除以分母,除不尽时,可以根据需要按“四舍五入”法保留几位小数。
回顾复习
6. 分数加、减法
同分母分数相加、减,分母不变,只把分子相加、减。异分母分数相加、减,先通分,然后按照同分母分数加、减法进行计算。计算的结果,能约分的要约成最简分数。
回顾复习
7. 分数加、减混合运算和简便运算
分数加减混合运算的顺序与整数加减混合运算的顺序相同。整数加法的交换律、结合律和减法的运算性质在分数加减法中同样适用。
当堂检测
56
79
87
195
204
630
22
31
57
65
78
83
1. 下面的数,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是质数?哪些是合数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
(教材P118练习二十八 第1题)
当堂检测
个位上是0,2,4,6,8的数都是2的倍数。
2的倍数:56、204、630、22、78;
5的倍数:195、630、65。
3的倍数:87、195、204、630、57、78;
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
个位上是0或5的数都是5的倍数。
当堂检测
一个数,如果只有1和它本身两个因数,这样的数叫作质数。
质数:79、31、83;
奇数:79、87、31、57、65、83;
合数:56、87、195、204、630、22、57、65、78;
一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。
整数中,是2的倍数的数叫作偶数(0也是0数),不是2的倍数的数叫作奇数。
偶数:56、204、630、22、78。
当堂检测
2. 食品店有70多个松花蛋。如果把它装进 4 个一排的蛋托中,正好装完;如果把它装进 6 个一排的蛋托中,也正好装完。一共有多少个松花蛋?(教材P118练习二十八 第4题)
4和6的公倍数有:12,24,36,48,60,72,
84…
已知食品店有70多个松花蛋,所以应该有72个松
花蛋。
答:食品店有72个松花蛋。
当堂检测
3. 计算。(教材P119练习二十八 第9题)
当堂检测
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
2023春人教版 数学
五年级下册
9 总复习
9.1 数与代数
1. 理解因数和倍数的意义,并能利用因数和倍数的知识解决实际问题。(重点)
2. 掌握分数的意义及其性质,并能进行分数的加法和减法。(难点)
学习目标
回顾复习
关于因数和倍数主要学习了哪些内容?
因数和倍数
因数和倍数
意义和特征
特征
2、5和3倍数的特征
奇数和偶数
倍数的求法
质数和合数
因数的求法
意义和特征
判断方法
回顾复习
1. 因数和倍数
一个数的因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。
回顾复习
2. 公因数和公倍数
几个数公有的倍数叫作它们的公倍数,其中最小的一个叫作它们的最小公倍数,没有最大的公倍数;几个数公有的因数叫作它们的公因数,最小的公因数是1,最大的公因数叫作它们的最大公因数。
回顾复习
3. 2、5、3的倍数的特征
个位上是0,2,4,6,8的数都是2的倍数。
一个数各位上的数的和是3的倍数就是3的倍数。
个位上是0、5的数都是5的倍数。
整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数。
4. 奇数和偶数
回顾复习
5. 质数和合数
一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数);一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。1既不是质数,也不是合数。
公因数只有1的两个数,叫作互质数。
6. 互质数
回顾复习
7. 最大公因数和最小公倍数
几个数公有的因数,叫作它们的公因数,其中最大的公因数,叫作它们的最大公因数。几个数公有的倍数,叫作它们的公倍数,其中最小的公倍数,叫作它们的最小公倍数。求最大公因数和最小公倍数常用的方法有:列举法、筛选法、分解质因数法和短除法。
回顾复习
关于分数主要学习了哪些内容?
分数
意义
分数的意义
分数的基本性质
性质
约分与通分
真分数和假分数
加减法
分数与除法
同分母分数加减法
异分母分数加减法
分数与小数的互化
回顾复习
1. 分数的意义
一个或一些物体都可以看作一个整体,用自然数 1 来表示,通常把它叫作单位“1”。把单位“1”平均分成若干份,表示其中一份的数叫作分数单位。
回顾复习
2. 分数与除法的关系
分数与除法的关系:被除数÷除数= 。
分子比分母小的分数叫作真分数。真分数小于1。分子比分母大或者分子和分母相等的分数,叫作假分数。假分数等于或大于1。由整数(不包括0)和真分数合成的数,通常叫作带分数。
3. 真分数和假分数
回顾复习
4. 约分和通分
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。
依据:分数的基本性质
把一个分数化成和它相等,但分子分母都比较小的分数,叫作约分。把异分母分数分别化成和原来分数相等的同分母分数,叫作通分。
回顾复习
5. 分数和小数的互化
小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数点去掉作分子。能约分的要约分。分数化成小数:要用分子除以分母,除不尽时,可以根据需要按“四舍五入”法保留几位小数。
回顾复习
6. 分数加、减法
同分母分数相加、减,分母不变,只把分子相加、减。异分母分数相加、减,先通分,然后按照同分母分数加、减法进行计算。计算的结果,能约分的要约成最简分数。
回顾复习
7. 分数加、减混合运算和简便运算
分数加减混合运算的顺序与整数加减混合运算的顺序相同。整数加法的交换律、结合律和减法的运算性质在分数加减法中同样适用。
当堂检测
56
79
87
195
204
630
22
31
57
65
78
83
1. 下面的数,哪些是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是质数?哪些是合数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
(教材P118练习二十八 第1题)
当堂检测
个位上是0,2,4,6,8的数都是2的倍数。
2的倍数:56、204、630、22、78;
5的倍数:195、630、65。
3的倍数:87、195、204、630、57、78;
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
个位上是0或5的数都是5的倍数。
当堂检测
一个数,如果只有1和它本身两个因数,这样的数叫作质数。
质数:79、31、83;
奇数:79、87、31、57、65、83;
合数:56、87、195、204、630、22、57、65、78;
一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。
整数中,是2的倍数的数叫作偶数(0也是0数),不是2的倍数的数叫作奇数。
偶数:56、204、630、22、78。
当堂检测
2. 食品店有70多个松花蛋。如果把它装进 4 个一排的蛋托中,正好装完;如果把它装进 6 个一排的蛋托中,也正好装完。一共有多少个松花蛋?(教材P118练习二十八 第4题)
4和6的公倍数有:12,24,36,48,60,72,
84…
已知食品店有70多个松花蛋,所以应该有72个松
花蛋。
答:食品店有72个松花蛋。
当堂检测
3. 计算。(教材P119练习二十八 第9题)
当堂检测
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
