(2023春)人教四年级数学下册1.1 加、减法的意义和各部分间的关系(课件)(共29张PPT)
文档属性
| 名称 | (2023春)人教四年级数学下册1.1 加、减法的意义和各部分间的关系(课件)(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 16:23:32 | ||
图片预览







文档简介
(共29张PPT)
1 四则运算
1.1 加、减法的意义和各部分间的关系
通过比较、概括等活动,掌握加、减法各部分间的关系。(重点)
2. 借助解决问题,经历总结加、减法的意义的过程,理解加、减法的意义。
(难点)
3. 在解决问题的过程中,培养逻辑推理能力及抽象、概括能力。
学习目标
情境导入
同学们,你们知道中国新世纪四大工程之一,被誉为“天路”的工程是什么吗?
情境导入
说一说:你能根据图中的信息提出哪些数学问题?
(教材P2 例1)
探索新知
1
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长814 km,格尔木到拉萨的铁路长1142 km。西宁到拉萨的铁路长多少千米?
西宁
格尔木
814 km
1142 km
拉萨
用什么方法计算?
探索新知
西宁到拉萨的铁路长多少千米?
814+1142
合并
=1956
什么是加法呢?
加数+
加数
=和
相加的两个数叫作加数。加得的数叫作和。
把两个数合并成一个数的运算,叫作加法。
(1)
西宁
格尔木
814 km
1142 km
拉萨
探索新知
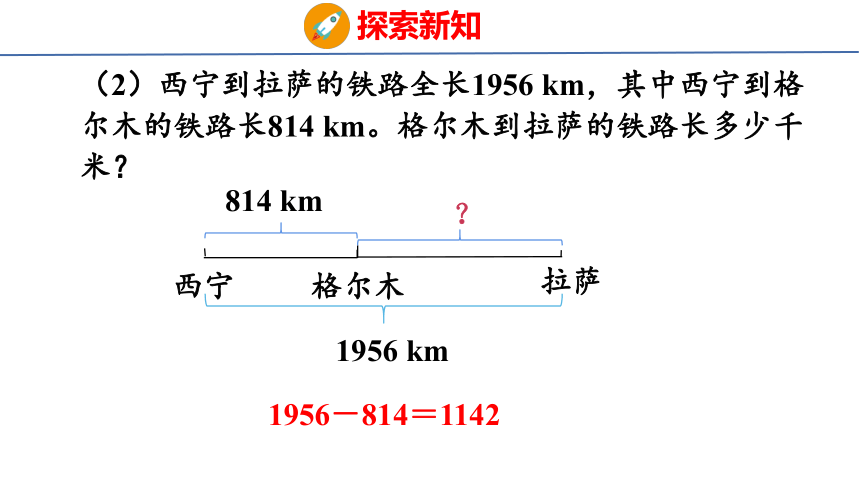
(2)西宁到拉萨的铁路全长1956 km,其中西宁到格尔木的铁路长814 km。格尔木到拉萨的铁路长多少千米?
西宁
格尔木
814 km
?
拉萨
1956 km
1956-814=1142
探索新知
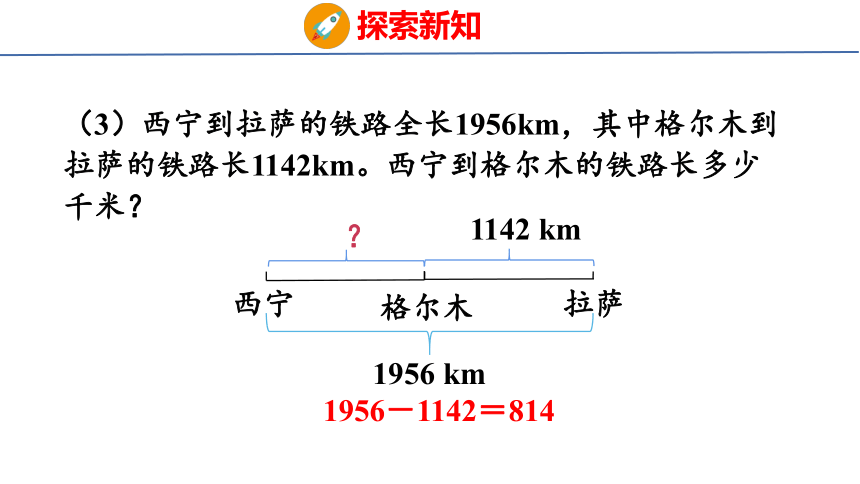
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨的铁路长1142km。西宁到格尔木的铁路长多少千米?
西宁
格尔木
1142 km
?
拉萨
1956 km
1956-1142=814
探索新知
问题:与第(1)题相比,第(2)、(3)题分别是已知什么?求什么?怎样算?
(1)814+1142=1956
(2)1956-814=1142
(3)1956-1142=814
第(2)、(3)题分别是已知两个数的和与其中的一个数,求另一个数。用减法计算。
探索新知
已知两个数的和与其中一个加数,求另一个加数的运算,叫作减法。
西宁
格尔木
814 km
?
拉萨
1956 km
(2)
(3)
1956-814=1142
1956-1142=814
西宁
格尔木
1142 km
?
拉萨
1956 km
探索新知
被减数 减数 差
- =
西宁
格尔木
814 km
?
拉萨
1956 km
(2)
(3)
1956-814=1142
1956-1142=814
西宁
格尔木
1142 km
?
拉萨
1956 km
在减法中,已知的和叫作被减数,已知的一个加数叫作减数,要求的另一个加数叫作差。
探索新知
加法与减法间的关系
(1)814+1142=1956
(3)1956-1142=814
(2)1956-814=1142
减法是加法的逆运算。
已知两个加数,求和用加法。
已知两个数的和与其中一个加数,求另一个加数,用减法。
探索新知
和=加数+加数
加数=和-另一个加数
问题:如果知道和与其中一个加数,能求出另一个加数吗?
加法各部分间的关系
探索新知
差=被减数-减数
问题:如果知道被减数和差,能求出减数吗?
减数=被减数-差
被减数=减数+差
问题:如果知道减数和差,能求出被减数吗?
减法各部分间的关系
探索新知
总 结
和=加数+加数
加数=和-另一个加数
差=被减数-减数
减数=被减数-差
被减数=减数+差
加法各部分间的关系
减法各部分间的关系
想一想,说一说:在刚才的计算过程中,有哪些注意事项?
已知部分量,求总量,用加法计算。
已知总量和一个部分量,求另一个部分量,用减法计算。
探索新知
减法是加法的逆运算。根据加、减法之间的互逆关系,可以进行加、减法算式的验算。
把两个数合并成一个数的运算,叫作加法。
相加的两个数叫作加数,加得的数叫作和。
加、减法的意义
探索新知
已知两个数的和与其中一个加数,求另一个加数的运算,叫作减法。
在减法中,已知的和叫作被减数,已知的一个加数叫作减数,要求的另一个加数叫作差。
探索新知
和=加数+加数
加数=和-另一个加数
差=被减数-减数
减数=被减数-差
被减数=减数+差
加法各部分间的关系
减法各部分间的关系
减法是加法的逆运算。
1.(教材P3 做一做 )
随堂小练
根据2468+575=3043,直接写出下面两道题的得数。
做一做
3043-2468=
3043-575=
2468
575
2.下列各题用什么方法计算?为什么?
(教材P4 练习一 第1题)
随堂小练
(1)滑雪场上午卖出86张门票,下午卖出59张门票。滑雪场全天一共卖出多少张门票?
(2)滑雪场全天一共卖出145张门票,其中上午卖出86张门票,下午卖出多少张门票?
加法 86+59=145(张)
减法 145-86=59(张)
随堂小练
(3)文具店购进一批练习本,卖出370本,剩下630本。文具店一共购进多少练习本?
(4)某小学一共有学生843人,其中男生有418人,女生有多少人?
加法 370+630=1000(本)
减法 843-418=425(人)
3.根据加、减法各部分间的关系,写出另外两个算式。
(教材P4 练习一 第2题)
随堂小练
28+19=47 47-19=28
47-28=19
203+147=350
67-55=12
850-239=611
350-203=147
350-147=203
850-611=239
611+239=850
67-12=55
12+55=67
1. 下面算式中的 代表的数分别是多少?
(教材P4 练习一 第3题)
当堂检测
19
+18=37 150+ =210 540- = 210
55+ =80 -73=100 200+ = 360
60
330
25
173
160
2. (教材P4 练习一 第4题)
当堂检测
500
143
273
511
654 - =
297
381
300
128
200 + =
400
851
200
500
328
651
154
357
当堂检测
3.小马虎在做一道减法题时,把减数72错写成了27,这时得到的差是265,正确的差是多少?
265+27=292
292-72=220
答:正确的差是220。
学习完本节课,你有什么收获?
课堂小结
通过本节课的学习,我们学习了加、减法的意义和各部分间的关系。
课堂小结
把两个数合并成一个数的运算,叫作加法。
相加的两个数叫作加数,加得的数叫作和。
已知两个数的和与其中一个加数,求另一个加数的运算,叫作减法。在减法中,已知的和叫作被减数,已知的一个加数叫作减数,要求的另一个加数叫作差。
通过本节课的学习,我们学习了加、减法的意义和各部分间的关系。
课堂小结
加、减法之间的关系:
和=加数+加数
加数=和-另一个加数
差=被减数-减数
被减数=减数+差
减数=被减数-差
加法各部分间的关系:
减法各部分间的关系:
减法是加法的逆运算。
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
1 四则运算
1.1 加、减法的意义和各部分间的关系
通过比较、概括等活动,掌握加、减法各部分间的关系。(重点)
2. 借助解决问题,经历总结加、减法的意义的过程,理解加、减法的意义。
(难点)
3. 在解决问题的过程中,培养逻辑推理能力及抽象、概括能力。
学习目标
情境导入
同学们,你们知道中国新世纪四大工程之一,被誉为“天路”的工程是什么吗?
情境导入
说一说:你能根据图中的信息提出哪些数学问题?
(教材P2 例1)
探索新知
1
(1)一列火车从西宁经过格尔木开往拉萨。西宁到格尔木的铁路长814 km,格尔木到拉萨的铁路长1142 km。西宁到拉萨的铁路长多少千米?
西宁
格尔木
814 km
1142 km
拉萨
用什么方法计算?
探索新知
西宁到拉萨的铁路长多少千米?
814+1142
合并
=1956
什么是加法呢?
加数+
加数
=和
相加的两个数叫作加数。加得的数叫作和。
把两个数合并成一个数的运算,叫作加法。
(1)
西宁
格尔木
814 km
1142 km
拉萨
探索新知
(2)西宁到拉萨的铁路全长1956 km,其中西宁到格尔木的铁路长814 km。格尔木到拉萨的铁路长多少千米?
西宁
格尔木
814 km
?
拉萨
1956 km
1956-814=1142
探索新知
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨的铁路长1142km。西宁到格尔木的铁路长多少千米?
西宁
格尔木
1142 km
?
拉萨
1956 km
1956-1142=814
探索新知
问题:与第(1)题相比,第(2)、(3)题分别是已知什么?求什么?怎样算?
(1)814+1142=1956
(2)1956-814=1142
(3)1956-1142=814
第(2)、(3)题分别是已知两个数的和与其中的一个数,求另一个数。用减法计算。
探索新知
已知两个数的和与其中一个加数,求另一个加数的运算,叫作减法。
西宁
格尔木
814 km
?
拉萨
1956 km
(2)
(3)
1956-814=1142
1956-1142=814
西宁
格尔木
1142 km
?
拉萨
1956 km
探索新知
被减数 减数 差
- =
西宁
格尔木
814 km
?
拉萨
1956 km
(2)
(3)
1956-814=1142
1956-1142=814
西宁
格尔木
1142 km
?
拉萨
1956 km
在减法中,已知的和叫作被减数,已知的一个加数叫作减数,要求的另一个加数叫作差。
探索新知
加法与减法间的关系
(1)814+1142=1956
(3)1956-1142=814
(2)1956-814=1142
减法是加法的逆运算。
已知两个加数,求和用加法。
已知两个数的和与其中一个加数,求另一个加数,用减法。
探索新知
和=加数+加数
加数=和-另一个加数
问题:如果知道和与其中一个加数,能求出另一个加数吗?
加法各部分间的关系
探索新知
差=被减数-减数
问题:如果知道被减数和差,能求出减数吗?
减数=被减数-差
被减数=减数+差
问题:如果知道减数和差,能求出被减数吗?
减法各部分间的关系
探索新知
总 结
和=加数+加数
加数=和-另一个加数
差=被减数-减数
减数=被减数-差
被减数=减数+差
加法各部分间的关系
减法各部分间的关系
想一想,说一说:在刚才的计算过程中,有哪些注意事项?
已知部分量,求总量,用加法计算。
已知总量和一个部分量,求另一个部分量,用减法计算。
探索新知
减法是加法的逆运算。根据加、减法之间的互逆关系,可以进行加、减法算式的验算。
把两个数合并成一个数的运算,叫作加法。
相加的两个数叫作加数,加得的数叫作和。
加、减法的意义
探索新知
已知两个数的和与其中一个加数,求另一个加数的运算,叫作减法。
在减法中,已知的和叫作被减数,已知的一个加数叫作减数,要求的另一个加数叫作差。
探索新知
和=加数+加数
加数=和-另一个加数
差=被减数-减数
减数=被减数-差
被减数=减数+差
加法各部分间的关系
减法各部分间的关系
减法是加法的逆运算。
1.(教材P3 做一做 )
随堂小练
根据2468+575=3043,直接写出下面两道题的得数。
做一做
3043-2468=
3043-575=
2468
575
2.下列各题用什么方法计算?为什么?
(教材P4 练习一 第1题)
随堂小练
(1)滑雪场上午卖出86张门票,下午卖出59张门票。滑雪场全天一共卖出多少张门票?
(2)滑雪场全天一共卖出145张门票,其中上午卖出86张门票,下午卖出多少张门票?
加法 86+59=145(张)
减法 145-86=59(张)
随堂小练
(3)文具店购进一批练习本,卖出370本,剩下630本。文具店一共购进多少练习本?
(4)某小学一共有学生843人,其中男生有418人,女生有多少人?
加法 370+630=1000(本)
减法 843-418=425(人)
3.根据加、减法各部分间的关系,写出另外两个算式。
(教材P4 练习一 第2题)
随堂小练
28+19=47 47-19=28
47-28=19
203+147=350
67-55=12
850-239=611
350-203=147
350-147=203
850-611=239
611+239=850
67-12=55
12+55=67
1. 下面算式中的 代表的数分别是多少?
(教材P4 练习一 第3题)
当堂检测
19
+18=37 150+ =210 540- = 210
55+ =80 -73=100 200+ = 360
60
330
25
173
160
2. (教材P4 练习一 第4题)
当堂检测
500
143
273
511
654 - =
297
381
300
128
200 + =
400
851
200
500
328
651
154
357
当堂检测
3.小马虎在做一道减法题时,把减数72错写成了27,这时得到的差是265,正确的差是多少?
265+27=292
292-72=220
答:正确的差是220。
学习完本节课,你有什么收获?
课堂小结
通过本节课的学习,我们学习了加、减法的意义和各部分间的关系。
课堂小结
把两个数合并成一个数的运算,叫作加法。
相加的两个数叫作加数,加得的数叫作和。
已知两个数的和与其中一个加数,求另一个加数的运算,叫作减法。在减法中,已知的和叫作被减数,已知的一个加数叫作减数,要求的另一个加数叫作差。
通过本节课的学习,我们学习了加、减法的意义和各部分间的关系。
课堂小结
加、减法之间的关系:
和=加数+加数
加数=和-另一个加数
差=被减数-减数
被减数=减数+差
减数=被减数-差
加法各部分间的关系:
减法各部分间的关系:
减法是加法的逆运算。
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
