(2023年春)人教四年级数学下册 鸡兔同笼课件(共31张PPT)
文档属性
| 名称 | (2023年春)人教四年级数学下册 鸡兔同笼课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-10 16:46:04 | ||
图片预览









文档简介
(共31张PPT)
9 数学广角——鸡兔同笼
鸡兔同笼
了解并经历解决“鸡兔同笼”问题的过程,培养逻辑推理能力。(重点)
能够运用列表、假设等方法解决“鸡兔同笼”问题,掌握解决问题的基本策略,提高分析问题和解决问题的能力,体会假设的思想方法。(难点)
感受古代数学问题的趣味性,培养学习数学的兴趣,增强应用意识和实践能力。
学习目标
情境导入
我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题 。
情境导入
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
今有雉兔同笼,上有三十五头,
下有九十四足,问雉兔各几何?
这道题的意思是:
情境导入
隐藏条件
兔有几只脚?
鸡有几只脚?
情境导入
请你猜一猜,大概有多少只鸡,多少只兔?
60只脚
40只脚
20只鸡,15只兔
+
= 100只脚
20只脚
60只脚
30只鸡,5只兔
+
= 80只脚
……
说一说:你猜到正确答案了吗? 你能想到一些比较好的方法吗?
情境导入
这节课我们学习鸡兔同笼。
学完本节课后,相信你会很快地算出上面题目的答案。
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。鸡和兔各有几只?
(教材P99 例1)
探索新知
1
从题中你了解到哪些信息?
1个头
1个头
4只脚
2只脚
头共有8个
总脚数是26只
鸡、兔各有几只
探索新知
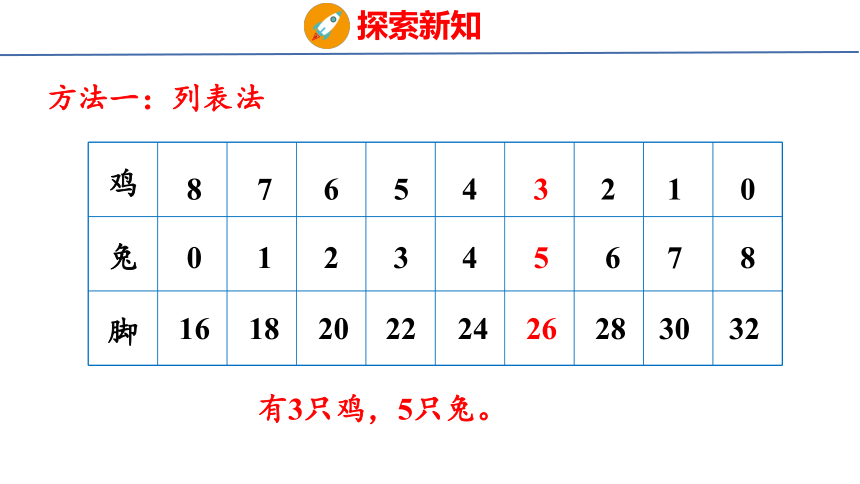
方法一:列表法
鸡
兔
脚
有3只鸡,5只兔。
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
探索新知
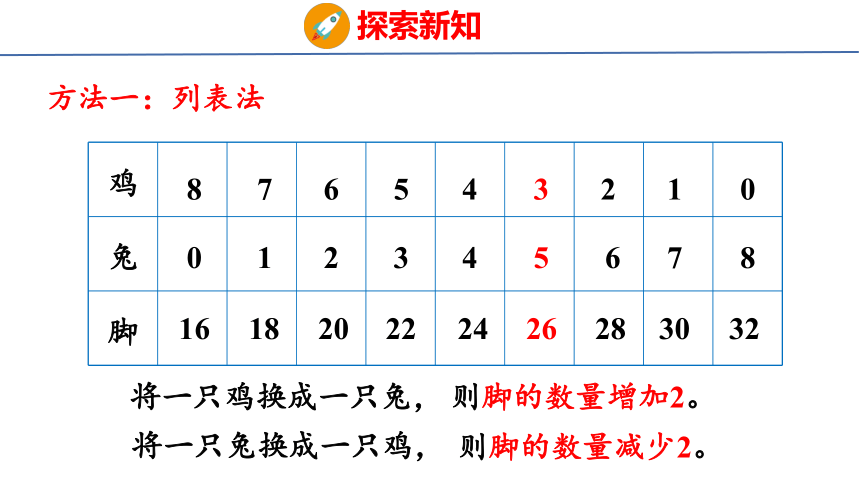
方法一:列表法
鸡
兔
脚
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
将一只鸡换成一只兔,
则脚的数量增加2。
将一只兔换成一只鸡,
则脚的数量减少2。
探索新知
方法二:假设法
(26-8×2)÷(4-2)
=(26-16)÷2
=10÷2
=5(只)
鸡的数量:8-5=3(只)
笼子里脚的数量是8×2=16(只)
与实际相差26-16=10(只)脚
每只兔子少算了2只,10÷2=5(只)就是兔子的数量。
答:5只兔子,3只鸡。
规范解答:
假设笼子都是鸡
探索新知
方法二:假设法
(8×4-26)÷(4-2)
=(32-26)÷2
=6÷2
=3(只)
兔子的数量:8-3=5(只)
笼子里脚的数量是8×4=32(只)
与实际相差32-26=6(只)脚
每只鸡多算了2只,6÷2=3(只)就是鸡的数量。
答:5只兔子,3只鸡。
规范解答:
假设笼子都是兔子
探索新知
方法三:抬脚法 —- 鸡抬起一只脚,兔子抬起两只脚。
(1)假如让鸡抬起一只脚,兔子抬起两只脚,
还有 26÷2=13只脚。
(2)脚的总数-头的总数=兔子的只数,
有13-8=5只兔子,有8-5=3只鸡。
答:5只兔子,3只鸡。
探索新知
笼子里有若干只鸡和兔,从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
方法一:假设笼子里全是鸡
(94-35×2)÷(4-2)
=(94-70)÷2
=24÷2
=12(只)
答:23只鸡,12只兔子。
鸡的数量:35-12=23(只)
探索新知
笼子里有若干只鸡和兔,从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
方法一:假设笼子里全是兔
答:23只鸡,12只兔子。
(35×4-94)÷(4-2)
=(140-94)÷2
=46÷2
=23(只)
兔子的数量:35-23=12(只)
想一想,说一说:在刚才“鸡兔同笼”计算过程中,有哪些注意事项?
假设笼子里全是鸡,先求出的是兔的只数;假设笼子里全是兔,先求出的是鸡的只数。
用“列表法”可以解决“鸡兔同笼”问题,但当数据较大时,解题过程比较繁琐,用假设法比较简便。
探索新知
解决“鸡兔同笼”问题,可以用列表法、假设法等多种方法。当题中数据较大时,用假设法比较简便。
鸡兔同笼
探索新知
列表法
鸡
兔
脚
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
假设法
探索新知
(1)如果笼子里都是鸡,那么就有8×2=16只脚,这样就多出26-16=10只脚。
(2)一只兔比一只鸡多2只脚,也就是有10÷2=5只兔。
(3)所以笼子里有3只鸡,5只兔。
(26-8×2)÷(4-2)
=(26-16)÷2
=10÷2
=5(只) 鸡的数量:8-5=3(只)
1.(教材P100 做一做 )
随堂小练
做一做
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆
假设全是三轮车
(10×3-26)÷(3-2)
=(30-26)÷1
=4÷1
=4(辆)
三轮车的数量:10-4=6(辆)
2.盒子里有大、小两种钢珠共30颗,共重266g。已知大钢珠每颗11g ,小钢珠每颗7g 。盒中大、小钢珠各有多少颗?(教材P101 练习二十四 第1题)
随堂小练
假设盒中全是大钢珠。
小钢珠:(11×30-266)÷(11-7)
=(330-266)÷4
= 64÷4
= 16(颗)
大钢珠: 30-16=14(颗)
3.有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?(教材P101 练习二十四 第2题)
随堂小练
(112-40×2)÷(4-2)
=(112-80)÷2
=32÷2
=16(只)
鹤的数量:40-16=24(只)
答:24只鹤,16只龟。
4.一共有38人,租了8条船,每条船都坐满了。大、小船各租了几条?(教材P101 练习二十四 第3题)
随堂小练
售票处
大船限乘6人
小船限乘4人
(38-8×4)÷(6-4)
=(38-32)÷2
=6÷2
=3(条)
小船的数量:8-3=5(条)
答:大船租了3条,小船租了5条。
1. 某小学“环保卫士”小分队12人参加植树活动。男生每人栽了3棵树,女生每人栽了2棵树,一共栽了32棵树。男生、女生各有几人?
(教材P4 练习一 第4题)
当堂检测
(32-12×2)÷(3-2)
=(32-24)÷1
=8÷1
=8(人) 男生的人数:12-8=4(人)
答:男生有4人,女生有8人。
2. 篮球比赛中,3分线外投中一球记3分,3分线内投中一球记2分。在一场比赛中张鹏投了15个球,进了9个,没有罚球,总共得了21分。张鹏在这场比赛中投进了几个3分球 (教材P101 练习二十四 第5题)
当堂检测
(21-9×2)÷(3-2)
=(21-18)÷1
=3÷1
=3(个)
答:张鹏在这场比赛中投进了3个3分球。
3. 花园路小学举办数学竞赛,试卷共有20道题,每做对一道题得5分,不做或做错一道题扣2分。壮壮共得79分,他做对了几道题?
当堂检测
(20×5-79)÷(5+2)=3(道)
20-3=17(道)
答:他做对了17道题。
4. 从前有座山,山里有座庙,庙里有许多和尚。两个小和尚用一根扁担一个桶抬水,一个大和尚用一根扁担两个桶挑水,共用了38根扁担和58个桶。抬水用了几根扁担?挑水呢?
当堂检测
抬水:(38×2-58)÷(2-1)=18(根)
挑水:38-18=20(根)
5. 军军花40元钱买了14张贺年卡与明信片,贺年卡每张3元5角,明信片每张2元5角。军军贺年卡、明信片各买了几张?
当堂检测
(400-25×14)÷(35-25)=5(张)
14-5=9(张)
答:军军贺年卡买了5张,明信片买了9张。
学习完本节课,你有什么收获?
课堂小结
通过本节课的学习,我们学习了“鸡兔同笼”。
课堂小结
解决“鸡兔同笼”问题,可以用列表法、假设法等多种方法。当题中数据较大时,用假设法比较简便。
列表法
鸡
兔
脚
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
通过本节课的学习,我们学习了“鸡兔同笼”。
课堂小结
假设法
(1)如果笼子里都是鸡,那么就有8×2=16只脚,这样就多出26-16=10只脚。
(2)一只兔比一只鸡多2只脚,也就是有10÷2=5只兔。
(3)所以笼子里有3只鸡,5只兔。
(26-8×2)÷(4-2)
=(26-16)÷2
=10÷2
=5(只) 鸡的数量:8-5=3(只)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
9 数学广角——鸡兔同笼
鸡兔同笼
了解并经历解决“鸡兔同笼”问题的过程,培养逻辑推理能力。(重点)
能够运用列表、假设等方法解决“鸡兔同笼”问题,掌握解决问题的基本策略,提高分析问题和解决问题的能力,体会假设的思想方法。(难点)
感受古代数学问题的趣味性,培养学习数学的兴趣,增强应用意识和实践能力。
学习目标
情境导入
我国古代数学名著《孙子算经》中记载了一道数学趣题——“鸡兔同笼”问题 。
情境导入
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
今有雉兔同笼,上有三十五头,
下有九十四足,问雉兔各几何?
这道题的意思是:
情境导入
隐藏条件
兔有几只脚?
鸡有几只脚?
情境导入
请你猜一猜,大概有多少只鸡,多少只兔?
60只脚
40只脚
20只鸡,15只兔
+
= 100只脚
20只脚
60只脚
30只鸡,5只兔
+
= 80只脚
……
说一说:你猜到正确答案了吗? 你能想到一些比较好的方法吗?
情境导入
这节课我们学习鸡兔同笼。
学完本节课后,相信你会很快地算出上面题目的答案。
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。鸡和兔各有几只?
(教材P99 例1)
探索新知
1
从题中你了解到哪些信息?
1个头
1个头
4只脚
2只脚
头共有8个
总脚数是26只
鸡、兔各有几只
探索新知
方法一:列表法
鸡
兔
脚
有3只鸡,5只兔。
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
探索新知
方法一:列表法
鸡
兔
脚
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
将一只鸡换成一只兔,
则脚的数量增加2。
将一只兔换成一只鸡,
则脚的数量减少2。
探索新知
方法二:假设法
(26-8×2)÷(4-2)
=(26-16)÷2
=10÷2
=5(只)
鸡的数量:8-5=3(只)
笼子里脚的数量是8×2=16(只)
与实际相差26-16=10(只)脚
每只兔子少算了2只,10÷2=5(只)就是兔子的数量。
答:5只兔子,3只鸡。
规范解答:
假设笼子都是鸡
探索新知
方法二:假设法
(8×4-26)÷(4-2)
=(32-26)÷2
=6÷2
=3(只)
兔子的数量:8-3=5(只)
笼子里脚的数量是8×4=32(只)
与实际相差32-26=6(只)脚
每只鸡多算了2只,6÷2=3(只)就是鸡的数量。
答:5只兔子,3只鸡。
规范解答:
假设笼子都是兔子
探索新知
方法三:抬脚法 —- 鸡抬起一只脚,兔子抬起两只脚。
(1)假如让鸡抬起一只脚,兔子抬起两只脚,
还有 26÷2=13只脚。
(2)脚的总数-头的总数=兔子的只数,
有13-8=5只兔子,有8-5=3只鸡。
答:5只兔子,3只鸡。
探索新知
笼子里有若干只鸡和兔,从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
方法一:假设笼子里全是鸡
(94-35×2)÷(4-2)
=(94-70)÷2
=24÷2
=12(只)
答:23只鸡,12只兔子。
鸡的数量:35-12=23(只)
探索新知
笼子里有若干只鸡和兔,从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
方法一:假设笼子里全是兔
答:23只鸡,12只兔子。
(35×4-94)÷(4-2)
=(140-94)÷2
=46÷2
=23(只)
兔子的数量:35-23=12(只)
想一想,说一说:在刚才“鸡兔同笼”计算过程中,有哪些注意事项?
假设笼子里全是鸡,先求出的是兔的只数;假设笼子里全是兔,先求出的是鸡的只数。
用“列表法”可以解决“鸡兔同笼”问题,但当数据较大时,解题过程比较繁琐,用假设法比较简便。
探索新知
解决“鸡兔同笼”问题,可以用列表法、假设法等多种方法。当题中数据较大时,用假设法比较简便。
鸡兔同笼
探索新知
列表法
鸡
兔
脚
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
假设法
探索新知
(1)如果笼子里都是鸡,那么就有8×2=16只脚,这样就多出26-16=10只脚。
(2)一只兔比一只鸡多2只脚,也就是有10÷2=5只兔。
(3)所以笼子里有3只鸡,5只兔。
(26-8×2)÷(4-2)
=(26-16)÷2
=10÷2
=5(只) 鸡的数量:8-5=3(只)
1.(教材P100 做一做 )
随堂小练
做一做
自行车和三轮车共10辆,总共有26个轮子。自行车和三轮车各有多少辆
假设全是三轮车
(10×3-26)÷(3-2)
=(30-26)÷1
=4÷1
=4(辆)
三轮车的数量:10-4=6(辆)
2.盒子里有大、小两种钢珠共30颗,共重266g。已知大钢珠每颗11g ,小钢珠每颗7g 。盒中大、小钢珠各有多少颗?(教材P101 练习二十四 第1题)
随堂小练
假设盒中全是大钢珠。
小钢珠:(11×30-266)÷(11-7)
=(330-266)÷4
= 64÷4
= 16(颗)
大钢珠: 30-16=14(颗)
3.有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?(教材P101 练习二十四 第2题)
随堂小练
(112-40×2)÷(4-2)
=(112-80)÷2
=32÷2
=16(只)
鹤的数量:40-16=24(只)
答:24只鹤,16只龟。
4.一共有38人,租了8条船,每条船都坐满了。大、小船各租了几条?(教材P101 练习二十四 第3题)
随堂小练
售票处
大船限乘6人
小船限乘4人
(38-8×4)÷(6-4)
=(38-32)÷2
=6÷2
=3(条)
小船的数量:8-3=5(条)
答:大船租了3条,小船租了5条。
1. 某小学“环保卫士”小分队12人参加植树活动。男生每人栽了3棵树,女生每人栽了2棵树,一共栽了32棵树。男生、女生各有几人?
(教材P4 练习一 第4题)
当堂检测
(32-12×2)÷(3-2)
=(32-24)÷1
=8÷1
=8(人) 男生的人数:12-8=4(人)
答:男生有4人,女生有8人。
2. 篮球比赛中,3分线外投中一球记3分,3分线内投中一球记2分。在一场比赛中张鹏投了15个球,进了9个,没有罚球,总共得了21分。张鹏在这场比赛中投进了几个3分球 (教材P101 练习二十四 第5题)
当堂检测
(21-9×2)÷(3-2)
=(21-18)÷1
=3÷1
=3(个)
答:张鹏在这场比赛中投进了3个3分球。
3. 花园路小学举办数学竞赛,试卷共有20道题,每做对一道题得5分,不做或做错一道题扣2分。壮壮共得79分,他做对了几道题?
当堂检测
(20×5-79)÷(5+2)=3(道)
20-3=17(道)
答:他做对了17道题。
4. 从前有座山,山里有座庙,庙里有许多和尚。两个小和尚用一根扁担一个桶抬水,一个大和尚用一根扁担两个桶挑水,共用了38根扁担和58个桶。抬水用了几根扁担?挑水呢?
当堂检测
抬水:(38×2-58)÷(2-1)=18(根)
挑水:38-18=20(根)
5. 军军花40元钱买了14张贺年卡与明信片,贺年卡每张3元5角,明信片每张2元5角。军军贺年卡、明信片各买了几张?
当堂检测
(400-25×14)÷(35-25)=5(张)
14-5=9(张)
答:军军贺年卡买了5张,明信片买了9张。
学习完本节课,你有什么收获?
课堂小结
通过本节课的学习,我们学习了“鸡兔同笼”。
课堂小结
解决“鸡兔同笼”问题,可以用列表法、假设法等多种方法。当题中数据较大时,用假设法比较简便。
列表法
鸡
兔
脚
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
通过本节课的学习,我们学习了“鸡兔同笼”。
课堂小结
假设法
(1)如果笼子里都是鸡,那么就有8×2=16只脚,这样就多出26-16=10只脚。
(2)一只兔比一只鸡多2只脚,也就是有10÷2=5只兔。
(3)所以笼子里有3只鸡,5只兔。
(26-8×2)÷(4-2)
=(26-16)÷2
=10÷2
=5(只) 鸡的数量:8-5=3(只)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
