第二章 整式的加减单元测试题(含答案)
文档属性
| 名称 | 第二章 整式的加减单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 252.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 12:55:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二章《整式的加减》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.下列代数式书写规范的是( )
A.a3 B. C.(a+b)÷c D.3a(x+1)
2.下列对于代数式2a+c的意义叙述正确的是( )
A.a的2倍与c的和 B.比a的2倍小c的数
C.a与c的和的2倍 D.a与c的2倍的和
3.下列各组整式中,不属于同类项的是( )
A.与 B.0.5a2b与0.5a2c
C.3abc与﹣3bca D.﹣1与2
4.下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y﹣z
C.x+2y﹣2z=x﹣2(z+y)
D.﹣a+c+d+b=﹣(a﹣b)﹣(﹣c﹣d)
5.若关于x的多项式(a-4)x3-xb+x-ab为二次三项式,则当x=-1时,这个二次三项式的值是( )
A.-8 B.-10 C.-12 D.-14
6.一个长方形的花园长为a,宽为b,如果长增加x,那么新的花园面积为( )
A.a(b+x) B.b(a+x) C.ab+x D.a+bx
7.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是( )
A.这个多项式是五次四项式
B.四次项的系数是7
C.常数项是1
D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+1
8.关于代数式,下列表述正确的是( )
A.单项式,次数为1 B.单项式,次数为2
C.多项式,次数为2 D.多项式,次数为3
9.已知m=a2+b2﹣1,n=2a﹣4b﹣6,则m与n的大小关系是( )
A.m≥n B.m>n C.m≤n D.m<n
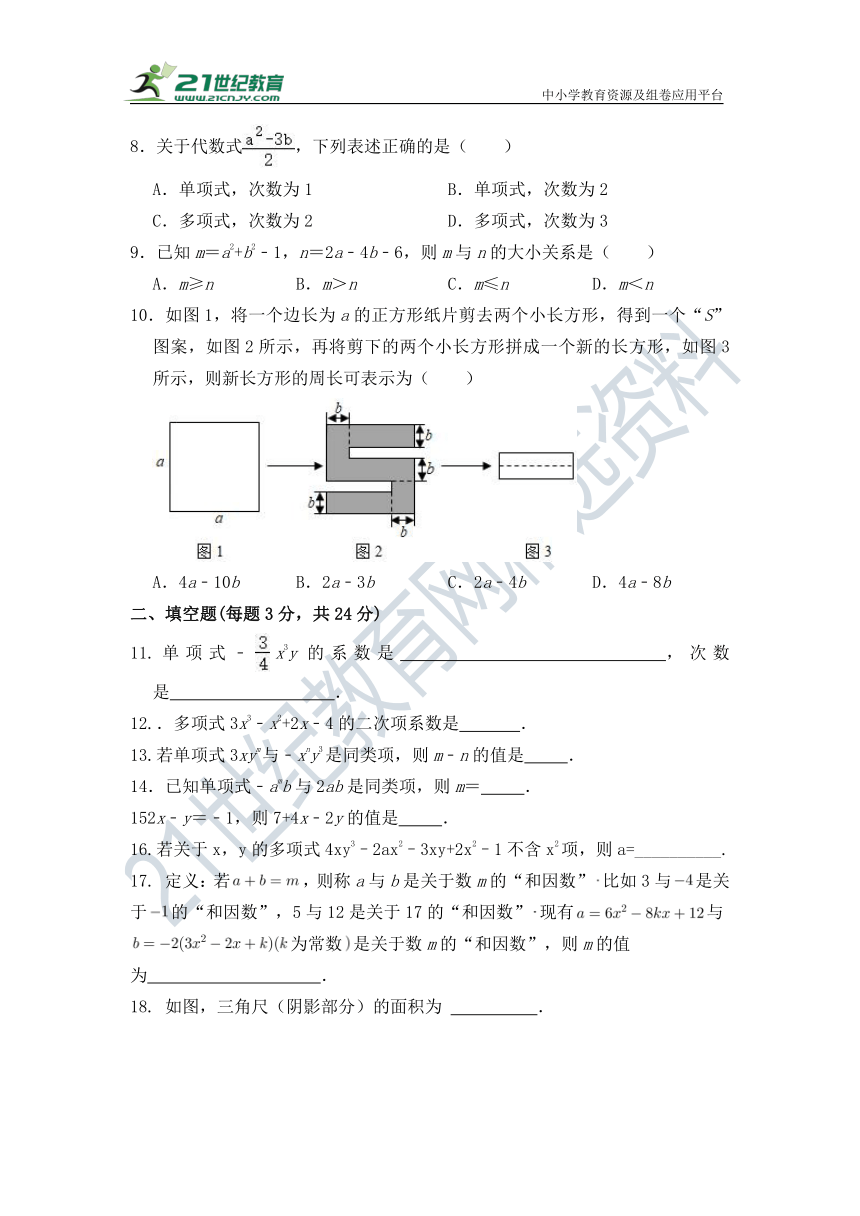
10.如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“S”图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为( )
A.4a﹣10b B.2a﹣3b C.2a﹣4b D.4a﹣8b
二、填空题(每题3分,共24分)
11.单项式﹣x3y的系数是 ,次数是 .
12..多项式3x3﹣x2+2x﹣4的二次项系数是 .
13.若单项式3xym与﹣xny3是同类项,则m﹣n的值是 .
14.已知单项式﹣amb与2ab是同类项,则m= .
152x﹣y=﹣1,则7+4x﹣2y的值是 .
16.若关于x,y的多项式4xy3–2ax2–3xy+2x2–1不含x2项,则a=__________.
17. 定义:若,则称a与b是关于数m的“和因数”比如3与是关于的“和因数”,5与12是关于17的“和因数”现有与为常数是关于数m的“和因数”,则m的值为 .
18. 如图,三角尺(阴影部分)的面积为 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.计算:
(1)
(2)
20.先化简,再求值:,其中.
21.已知:A-B=-ab,且B=-+6ab+1.
(1)求A等于多少
(2)若与是同类项,求A的值.
22.已知关于x,y的多项式x4+(m+2)xny-xy2+3,其中n为正整数.
(1)当m,n为何值时,它是五次四项式?
(2)当m,n为何值时,它是四次三项式?
23.如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:
菜地的长______米,宽______米;
菜地的面积______平方米;
求当米时,菜地的面积.
24.把千位数字为a、百位数字为b、十位数字为c、个位数字为d的四位整数记为,若千位与百位数之和等于常数k(k为正整数),十位与个位数字之和等于k﹣1(即a+b=k,c+d=k﹣1),那么,称这个四位整数为“k类递进数”,例如:3213是“5类递进数”,因为3+2=5,1+3=4,5﹣4=l;5427不是“9类递进数”,因为5+4=9,2+7=9,9﹣9≠1.
(1)写出最小的“3类递进数”是 ,最大的“7类递进数”是 .
(2)若一个“6类递进数”,且﹣=19(a,c≠0),求满足条件的所有“6类递进数”的个数,并把它们写出来.
参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B D B B B C A D
二.填空题
11:单项式﹣x3y的系数是﹣,次数是4,
故答案为:﹣;4.
12:∵多项式3x3﹣x2+2x﹣4的二次项是﹣x2,
∴二次项系数为:﹣1.
故答案为:﹣1.
13.3xym与﹣xny3是同类项,
∴m=3,n=1,
∴m﹣n=3﹣1=2.
故答案为:2.
14:∵单项式﹣amb与2ab是同类项,
∴m=1.
故答案为:1.
15:7+4x﹣2y
=7+2(2x﹣y),
当2x﹣y=﹣1时,
∴原式=7+2×(﹣1)=5.
故答案为:5.
16.答案为:1
7. 11
18、
三.解答题
19.(1);(2)
【解析】解:(1)
=
=
(2)
=
=
=.
20.;4
【解析】解:原式,
,
把代入得,
原式;
21.(1)5ab+1;(2)16
【解析】解:(1)∵A-B=-ab,且B=-+6ab+1,
∴A=B+(a2﹣ab)
=(﹣a2+6ab+1)+(a2﹣ab)
=﹣a2+6ab+1+a2﹣ab
=5ab+1;
(2)由题意可知:2a=2,b+1=a+3,
即a=1,b=3,
当a=1,b=3时,
原式=5×1×3+1
=16.
22.解:(1)因为多项式是五次四项式,
所以n+1=5,m+2≠0,
所以n=4,m≠-2.
(2)因为多项式是四次三项式,
所以m+2=0,n为任意正整数,
所以m=-2,n为任意正整数.
23.,;
;
由得菜地的面积为:,
当时,.
24.解:(1)最小的“3类递进数”是1202,
∵根据题意,此数为四位数,且k=3,
∴a+b=3,c+d=2,
∵该数最小,
∴a=1,b=2,c=0,d=2,
∴最小的“3类递进数”是1202,
最大的“7类递进数”是7060,
∵根据题意,此数为四位数,且k=7,
∴a+b=7,c+d=6,
∵该数最大,
∴a=7,b=0,c=6,d=0,
∴最小的“7类递进数”是7060;
故答案为:1202,7060.
(2)①∵k=6,
∴a+b=6,c+d=5,
∵﹣=19(a,c≠0),
∵10a+b﹣10c﹣d=19,
∴a﹣c=2,
∴a≥2,
当a=2时,b=4,
∵﹣=19
∴c=0,d=5(舍去),
当a=3时,b=3,
∵﹣=19
∴c=1,d=4,
当a=4时,b=2,
∵﹣=19
∴c=2,d=3,
当a=5时,b=1,
∵﹣=19
∴c=3,d=2,
当a=6时,b=0,
∵﹣=19
∴c=4,d=1,
∴满足条件的所有“6类递进数”的个数有4个,分别是:3314,4223,5132,6041.
www.21cnjy.com 精品试卷·第 2 页 (共 4 页)
第二章《整式的加减》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.下列代数式书写规范的是( )
A.a3 B. C.(a+b)÷c D.3a(x+1)
2.下列对于代数式2a+c的意义叙述正确的是( )
A.a的2倍与c的和 B.比a的2倍小c的数
C.a与c的和的2倍 D.a与c的2倍的和
3.下列各组整式中,不属于同类项的是( )
A.与 B.0.5a2b与0.5a2c
C.3abc与﹣3bca D.﹣1与2
4.下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y﹣z
C.x+2y﹣2z=x﹣2(z+y)
D.﹣a+c+d+b=﹣(a﹣b)﹣(﹣c﹣d)
5.若关于x的多项式(a-4)x3-xb+x-ab为二次三项式,则当x=-1时,这个二次三项式的值是( )
A.-8 B.-10 C.-12 D.-14
6.一个长方形的花园长为a,宽为b,如果长增加x,那么新的花园面积为( )
A.a(b+x) B.b(a+x) C.ab+x D.a+bx
7.关于多项式0.3x2y﹣2x3y2﹣7xy3+1,下列说法错误的是( )
A.这个多项式是五次四项式
B.四次项的系数是7
C.常数项是1
D.按y降幂排列为﹣7xy3﹣2x3y2+0.3x2y+1
8.关于代数式,下列表述正确的是( )
A.单项式,次数为1 B.单项式,次数为2
C.多项式,次数为2 D.多项式,次数为3
9.已知m=a2+b2﹣1,n=2a﹣4b﹣6,则m与n的大小关系是( )
A.m≥n B.m>n C.m≤n D.m<n
10.如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“S”图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,则新长方形的周长可表示为( )
A.4a﹣10b B.2a﹣3b C.2a﹣4b D.4a﹣8b
二、填空题(每题3分,共24分)
11.单项式﹣x3y的系数是 ,次数是 .
12..多项式3x3﹣x2+2x﹣4的二次项系数是 .
13.若单项式3xym与﹣xny3是同类项,则m﹣n的值是 .
14.已知单项式﹣amb与2ab是同类项,则m= .
152x﹣y=﹣1,则7+4x﹣2y的值是 .
16.若关于x,y的多项式4xy3–2ax2–3xy+2x2–1不含x2项,则a=__________.
17. 定义:若,则称a与b是关于数m的“和因数”比如3与是关于的“和因数”,5与12是关于17的“和因数”现有与为常数是关于数m的“和因数”,则m的值为 .
18. 如图,三角尺(阴影部分)的面积为 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.计算:
(1)
(2)
20.先化简,再求值:,其中.
21.已知:A-B=-ab,且B=-+6ab+1.
(1)求A等于多少
(2)若与是同类项,求A的值.
22.已知关于x,y的多项式x4+(m+2)xny-xy2+3,其中n为正整数.
(1)当m,n为何值时,它是五次四项式?
(2)当m,n为何值时,它是四次三项式?
23.如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:
菜地的长______米,宽______米;
菜地的面积______平方米;
求当米时,菜地的面积.
24.把千位数字为a、百位数字为b、十位数字为c、个位数字为d的四位整数记为,若千位与百位数之和等于常数k(k为正整数),十位与个位数字之和等于k﹣1(即a+b=k,c+d=k﹣1),那么,称这个四位整数为“k类递进数”,例如:3213是“5类递进数”,因为3+2=5,1+3=4,5﹣4=l;5427不是“9类递进数”,因为5+4=9,2+7=9,9﹣9≠1.
(1)写出最小的“3类递进数”是 ,最大的“7类递进数”是 .
(2)若一个“6类递进数”,且﹣=19(a,c≠0),求满足条件的所有“6类递进数”的个数,并把它们写出来.
参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B D B B B C A D
二.填空题
11:单项式﹣x3y的系数是﹣,次数是4,
故答案为:﹣;4.
12:∵多项式3x3﹣x2+2x﹣4的二次项是﹣x2,
∴二次项系数为:﹣1.
故答案为:﹣1.
13.3xym与﹣xny3是同类项,
∴m=3,n=1,
∴m﹣n=3﹣1=2.
故答案为:2.
14:∵单项式﹣amb与2ab是同类项,
∴m=1.
故答案为:1.
15:7+4x﹣2y
=7+2(2x﹣y),
当2x﹣y=﹣1时,
∴原式=7+2×(﹣1)=5.
故答案为:5.
16.答案为:1
7. 11
18、
三.解答题
19.(1);(2)
【解析】解:(1)
=
=
(2)
=
=
=.
20.;4
【解析】解:原式,
,
把代入得,
原式;
21.(1)5ab+1;(2)16
【解析】解:(1)∵A-B=-ab,且B=-+6ab+1,
∴A=B+(a2﹣ab)
=(﹣a2+6ab+1)+(a2﹣ab)
=﹣a2+6ab+1+a2﹣ab
=5ab+1;
(2)由题意可知:2a=2,b+1=a+3,
即a=1,b=3,
当a=1,b=3时,
原式=5×1×3+1
=16.
22.解:(1)因为多项式是五次四项式,
所以n+1=5,m+2≠0,
所以n=4,m≠-2.
(2)因为多项式是四次三项式,
所以m+2=0,n为任意正整数,
所以m=-2,n为任意正整数.
23.,;
;
由得菜地的面积为:,
当时,.
24.解:(1)最小的“3类递进数”是1202,
∵根据题意,此数为四位数,且k=3,
∴a+b=3,c+d=2,
∵该数最小,
∴a=1,b=2,c=0,d=2,
∴最小的“3类递进数”是1202,
最大的“7类递进数”是7060,
∵根据题意,此数为四位数,且k=7,
∴a+b=7,c+d=6,
∵该数最大,
∴a=7,b=0,c=6,d=0,
∴最小的“7类递进数”是7060;
故答案为:1202,7060.
(2)①∵k=6,
∴a+b=6,c+d=5,
∵﹣=19(a,c≠0),
∵10a+b﹣10c﹣d=19,
∴a﹣c=2,
∴a≥2,
当a=2时,b=4,
∵﹣=19
∴c=0,d=5(舍去),
当a=3时,b=3,
∵﹣=19
∴c=1,d=4,
当a=4时,b=2,
∵﹣=19
∴c=2,d=3,
当a=5时,b=1,
∵﹣=19
∴c=3,d=2,
当a=6时,b=0,
∵﹣=19
∴c=4,d=1,
∴满足条件的所有“6类递进数”的个数有4个,分别是:3314,4223,5132,6041.
www.21cnjy.com 精品试卷·第 2 页 (共 4 页)
