6.1 平方根 课件

课件21张PPT。6.1平方根问题1：装修房屋，选用了某种型号的正方形地砖，这种地砖4块正好铺1cm2 ，如图，问这种地砖一块的边长是多少？S=1㎝2X2 =1/4数的开方复习平方、乘方:（2）42= ，（－4）2= ；（3） ， ；（4）（0.8）2= ， （－0.8）2= 。（1）什么叫乘方？ 答：求相同因数的积的运算叫做乘方。16160.640.64显然乘方是已知底数和指数，求幂。如： 42已知底数4及指数2，求幂16。 反过来：如果已知一个数平方等于16，怎样求这个数？即知已指数2及幂16，求底数？？ ( ？ )2=16解：设这个数为x则 x 2 =16∵4 2 = 16，（－4）2 = 16∴ x = 4 或 －4 因为4 、－4的平方都等于16，我们把4及－4叫做16的平方根。同理： 的平方等于 。那么 叫 的平方根。 0.8、－ 0.8的平方等于0.64。那么 叫
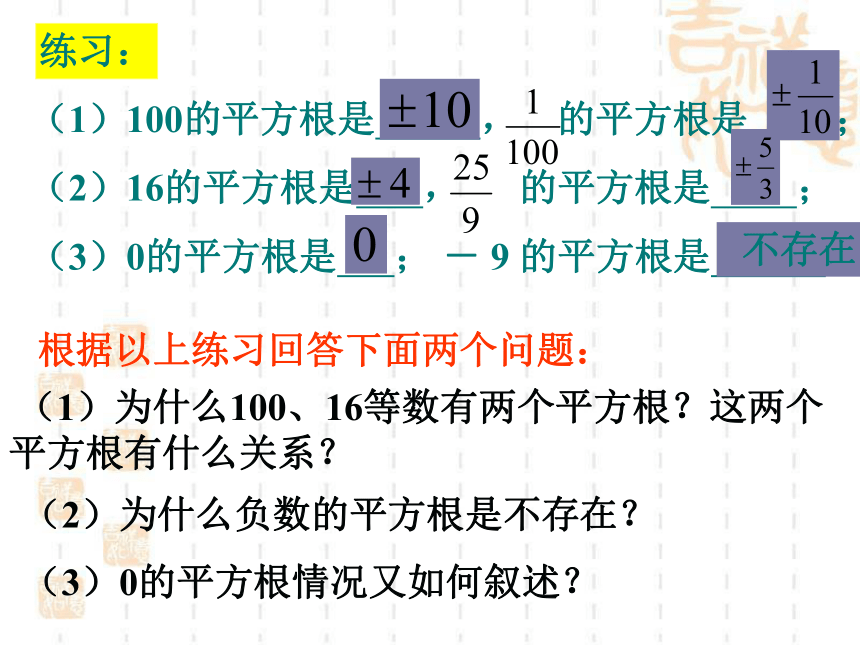
的平方根。0.8、－ 0.80.64什么叫数的平方根？？？（1）100的平方根是 ， 的平方根是 ；
（2）16的平方根是 ， 的平方根是 ；
（3）0的平方根是 ； － 9 的平方根是 。练习：不存在 （1）为什么100、16等数有两个平方根？这两个平方根有什么关系？（2）为什么负数的平方根是不存在？根据以上练习回答下面两个问题：（3）0的平方根情况又如何叙述？归纳：（1） 一个正数有两个平方根，且互为相反数；
（2） 零只有一个平方根；?
（3） 负数没有平方根．? 前面的问题解决了吗?X2 =1/4一个正数a的平方根表示方法:（1）当a > 0时， a的正的平方根用符号“ ”表示。a负平方根用符号表示 “ ”总之：正数a的平方根是 。读作：二次根号a读作：正负二次根号a0；（2）当a = 0时， 0；一个非负数a的表示方法: 当a ≥ 0时， a的正的平方根用符号“ ”表示。a负平方根用符号表示 “ ”总之：非负数a的平方根是 。读作：二次根号a读作：正负二次根号a一个非负数a的表示方法: 当a ≥ 0时， a的正的平方根用符号“ ”表示。被开方数a负平方根用符号表示 “ ”总之：非负数a的平方根是 。读作：根号读作：根号a读作：正负根号a如果x2=a,那么a的平方根表示为x=例如：2的平方根记作 ，读作：正负根号2算术平方根0 的算术平方根也是 0未解决的问题:（1）平方根是怎样产生的？（2）平方根的本质是什么？是一种运算方法？是一个数？。。。。。求一个数的平方根的运算叫开平方。开平方与平方是互为逆运算正数与零任何数幂平方根开平方平方运算符号适用范围运算结果名称性质正数有 个平方根,它们是 ,零的平方根是 , 负数 .正数的平方是 数; 零的平方是 ; 负数的平方是 数.正正02互为相反数0没有平方根例1 求下列各数的平方根:（1） 81 （2）100 （3） （4）0.49 （5）169分析 问：解题思想方法是？答：根据平方根的定义，把求平方根转化为求平方。即求出平方等于81的所有数。解：
（1）∵ 即∴81的平方根是例2 下列各数有平方根吗？如果有，求出它的平方根；如果没有，请说明理由。（1）－64 （2）0 （3）（－4）2解：（1）因为－64是负数，所以－64没有平方根（2）0有一个平方根，它是0；（3）因为（－4）2=16所以（－4）2的平方根就是16的平方根因此的（－4）2平方根是（1）因为 ，所以 是 的平方根；
（2） 时 ， 0 ； 0 。 一、概念理解填空题：（3）0的平方根可以理解成： ；
。所以概括为 。000巩固练习:
二、选择题：
1、在0、－9、2、（－2）2 中，有平方根的是（ ）
A、1个 B、2个 C、3个 D、4个
2、数16的平方根是（ ）
A、4 B、 C、 －4 D、4或－4
3、数0.25的平方根是（ ）
A、0.5 B、0.05 C、－0.5 D、0.5或－0.5
4、数（－6）2的平方根是（ ）
A、－6 B、6 C、6或－6 D、无平方根
CDDC三、判断题：（1）144的平方根是－12与12；（2）256的平方根是16；（3）－5是25的一个平方根；（4）1的平方根是1；（5）－1的平方根是－1；（6）－1是1的平方根；（7）（－1）2的平方根－1。√×√√×××小结1、如果 ，那么 就叫做 的平方根，用 来
表示。当 时，有两个平方根，即 ， 表
示 的正的平方根，即算术平方根， 表示负平方根。
2、开平方与平方