1.3 平抛运动 课件-2022-2023学年高一下学期物理粤教版(2019)必修第二册(25页ppt)
文档属性
| 名称 | 1.3 平抛运动 课件-2022-2023学年高一下学期物理粤教版(2019)必修第二册(25页ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 63.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-01-10 21:42:40 | ||
图片预览



文档简介
1.3 平抛运动
v0
G
一. 什么是平抛运动
1. 定义:将物体以一定的初速度沿水平方向抛出,仅在重力作用下物体所做的运动叫做平抛运动。
2. 运动特征:
①初速度——v0≠0且沿水平方向
②合外力——F合=G
(理想化模型)
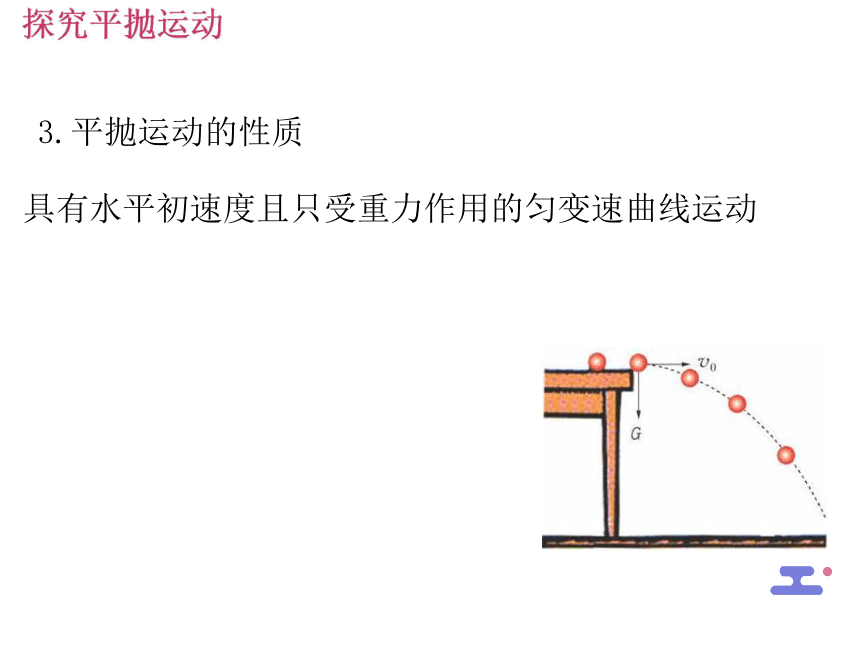
探究平抛运动
3.平抛运动的性质
具有水平初速度且只受重力作用的匀变速曲线运动
√
探究平抛运动
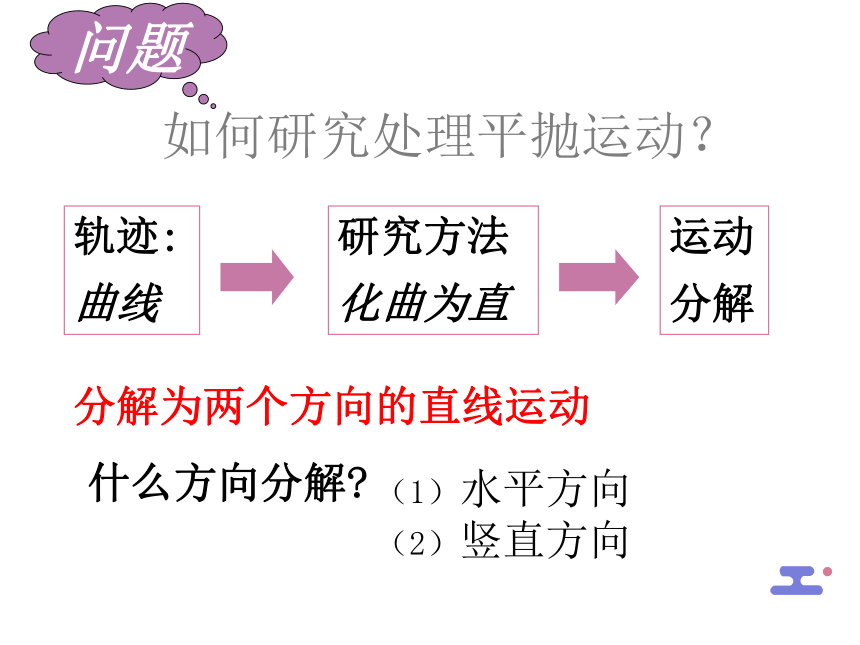
如何研究处理平抛运动?
分解为两个方向的直线运动
轨迹:
曲线
问题
研究方法
化曲为直
运动
分解
(1)水平方向
(2)竖直方向
什么方向分解?
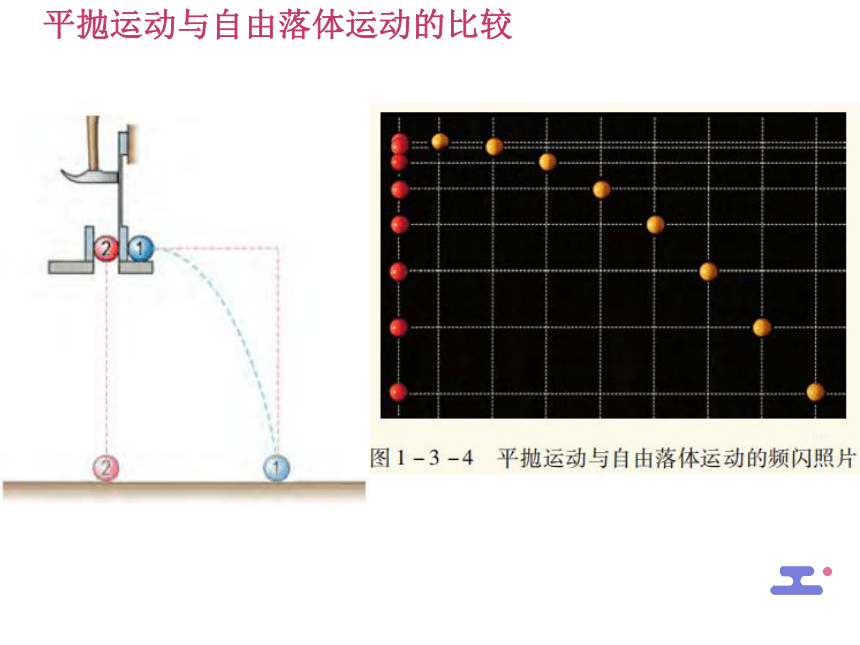
平抛运动与自由落体运动的比较
研究平抛运动
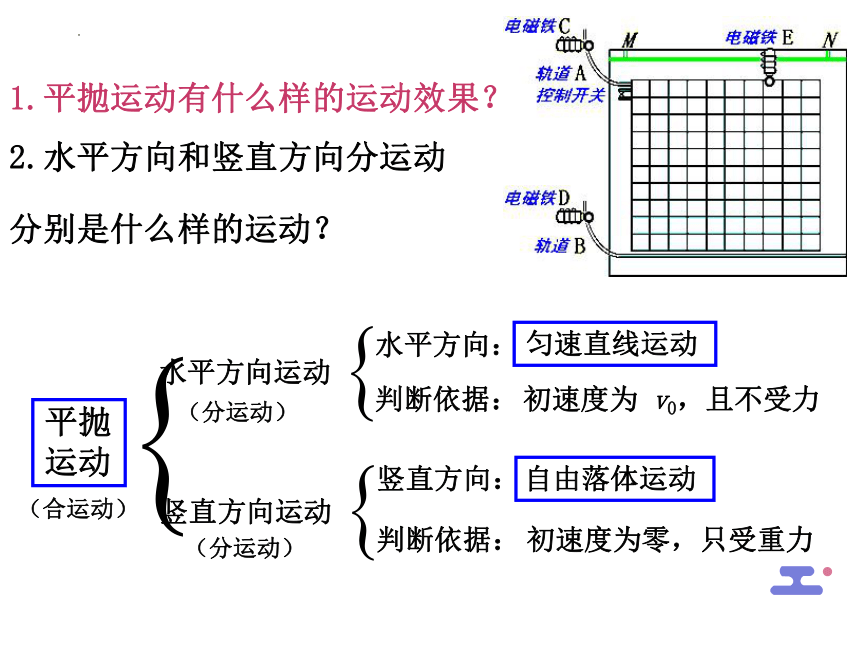
1.平抛运动有什么样的运动效果?
平抛运动
水平方向运动
竖直方向运动
2.水平方向和竖直方向分运动
分别是什么样的运动?
水平方向:
判断依据:
初速度为 v0,且不受力
匀速直线运动
竖直方向:
判断依据:
初速度为零,只受重力
自由落体运动
(分运动)
(分运动)
(合运动)
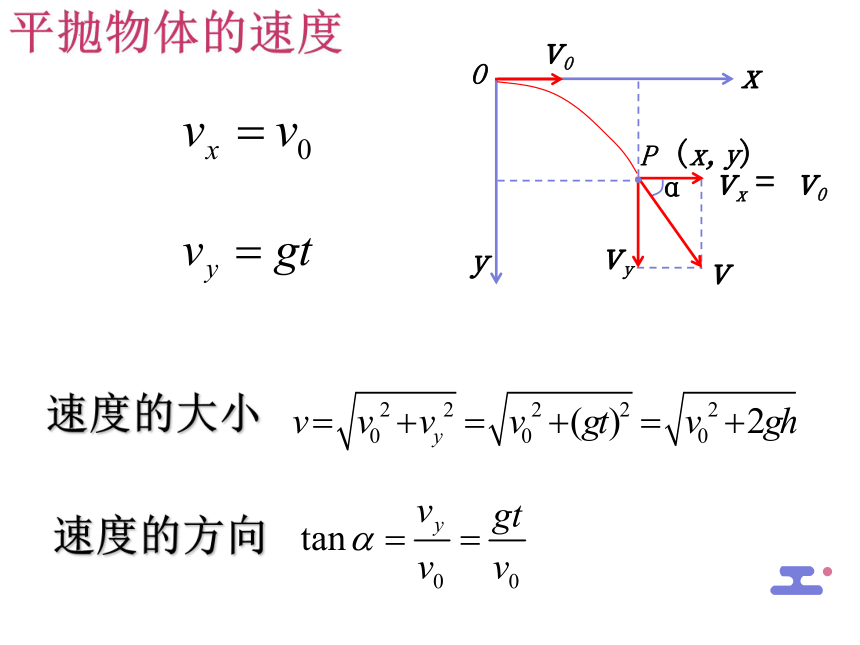
速度的大小
速度的方向
α
vx = v0
vy
v
O
x
y
v0
P (x,y)
平抛物体的速度
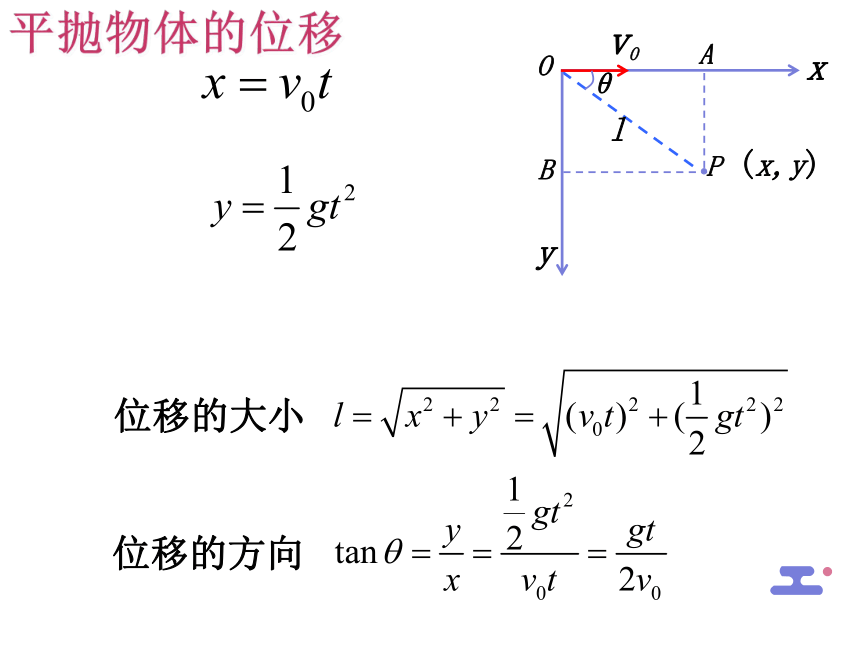
位移的大小
位移的方向
l
O
x
y
P (x,y)
B
A
v0
θ
平抛物体的位移
O
y
B
x
A
P (x,y)
v0
1、位移偏向角θ与速度偏向角α有什么关系?
2、速度方向的反向延长线与 x 轴的交点O ′有什么特点?
位移偏向角θ:
速度偏向角α:
速度方向的反向延长线与x轴的交点为水平位移的中点。
l
θ
α
vx = v0
α
v
vy
O′
思考
平抛物体的轨迹
物体在P 点的坐标
y = x2
2v02
g
O
x
y
v0
P (x,y)
平抛运动的轨迹一条抛物线
平抛运动题型
1.基础计算(无θ角);
2.带角度θ计算。
基础计算(无θ角)步骤
Y :
X:
如图所示,摩托车特技表演,从平台A水平飞越到平台B上,已知AB的高度差为h=1.25m,网平台的水平距离为s=5m,(不计空气阻力,g取10m/s2)求:
(1)摩托车在空中运动时间;
(2)摩托车在平台A开始飞越时的最小速度。
Y :
X:
将一个小球以10m/s的速度沿水平方向抛出,小球经过1s的时间落地.不计空气阻力作用求
(1)抛出点与落地点在竖直方向的高度差;
(2)小球落地时的速度大小,以及速度与水平方向夹角。
Y :
X:
速度的大小
如图所示,水平屋顶高H=5m,墙高h=3.2m,墙到房子的距离L=3m,墙外马路宽x=10m,小球从房顶a点水平飞出,(取g=10m/s2)
(1)若小球落在墙外的马路上,求小球在空中运动的时间;
(2)若小球恰好经过墙顶b点后落在马路上,求小球离开房顶时的速度v0
(3)若小球落在墙外的马路上,求小球离开房顶时的速度v0的取值范围
Y :
X:
带角度θ计算步骤
Y :
X:
①
②
通过角度把XY两个方向的位移或速度进行几何关系(或三角函数)联系。
③
a.画出水平位移和竖直位移,找角度关系;
b.画出水平速度和竖直速度,找角度关系。
PS:速度偏转角关键字——恰好、相切、垂直
如图,从倾角θ的斜面顶端以初速度v0水平抛出小球,小球落在斜面上,求:
(1)小球空中飞行的时间;
(2)小球落点与抛出点间的距离。
v0
θ
小球以15m/s的水平速度抛向倾角37°的斜面,飞行一段时间后,恰好垂直撞到斜面上,g=10m/s2,求:
(1)小球空中飞行的时间;
(2)小球落点与抛出点间的高度。
v0
小球以水平速度v0抛出,飞行一段时间后,恰好不和挡板碰撞,重力加速度g,求小球运动轨迹与挡板M相距最近时对应的运动时间。
v0
M
θ
如图,平台顶端以初速度v0=8m/s水平抛出小球,恰好落在平台前倾角θ=37°的斜面顶端,并刚好沿着斜面下滑,已知平台高度与斜坡A点竖直相距h1 = 1.8m,斜面高度h2=14.4m,小球与斜面动摩擦因素为0.5,g = 10m/s2,忽略空气。求:
(1)小球空中飞行的时间以及刚落到斜面的速度;
(2)小球从平台抛出运动到B点的时间。
v0
θ
A
B
o
解:(1)急救用品做平抛运动,在竖直方向上做自由落体运动,有
得
急救用品在水平方向上做匀速直线运动,在t时间内的水平位移
(2)设急救用品落在水平面上时竖直方向速度的大小为
急救用品落在水平面时,速度的大小
滑雪运动员以20m/s的水平速度从一山坡飞出,问经过多长时间又落到斜坡上。已知斜坡与水平面成45°角落,取g=10m/s2。
x
y
450
A
B
解:滑雪运动可视为做平抛运动,如图,设经时间t落到斜坡上,有
由几何关系
即 y=x
得
练习
v0
G
一. 什么是平抛运动
1. 定义:将物体以一定的初速度沿水平方向抛出,仅在重力作用下物体所做的运动叫做平抛运动。
2. 运动特征:
①初速度——v0≠0且沿水平方向
②合外力——F合=G
(理想化模型)
探究平抛运动
3.平抛运动的性质
具有水平初速度且只受重力作用的匀变速曲线运动
√
探究平抛运动
如何研究处理平抛运动?
分解为两个方向的直线运动
轨迹:
曲线
问题
研究方法
化曲为直
运动
分解
(1)水平方向
(2)竖直方向
什么方向分解?
平抛运动与自由落体运动的比较
研究平抛运动
1.平抛运动有什么样的运动效果?
平抛运动
水平方向运动
竖直方向运动
2.水平方向和竖直方向分运动
分别是什么样的运动?
水平方向:
判断依据:
初速度为 v0,且不受力
匀速直线运动
竖直方向:
判断依据:
初速度为零,只受重力
自由落体运动
(分运动)
(分运动)
(合运动)
速度的大小
速度的方向
α
vx = v0
vy
v
O
x
y
v0
P (x,y)
平抛物体的速度
位移的大小
位移的方向
l
O
x
y
P (x,y)
B
A
v0
θ
平抛物体的位移
O
y
B
x
A
P (x,y)
v0
1、位移偏向角θ与速度偏向角α有什么关系?
2、速度方向的反向延长线与 x 轴的交点O ′有什么特点?
位移偏向角θ:
速度偏向角α:
速度方向的反向延长线与x轴的交点为水平位移的中点。
l
θ
α
vx = v0
α
v
vy
O′
思考
平抛物体的轨迹
物体在P 点的坐标
y = x2
2v02
g
O
x
y
v0
P (x,y)
平抛运动的轨迹一条抛物线
平抛运动题型
1.基础计算(无θ角);
2.带角度θ计算。
基础计算(无θ角)步骤
Y :
X:
如图所示,摩托车特技表演,从平台A水平飞越到平台B上,已知AB的高度差为h=1.25m,网平台的水平距离为s=5m,(不计空气阻力,g取10m/s2)求:
(1)摩托车在空中运动时间;
(2)摩托车在平台A开始飞越时的最小速度。
Y :
X:
将一个小球以10m/s的速度沿水平方向抛出,小球经过1s的时间落地.不计空气阻力作用求
(1)抛出点与落地点在竖直方向的高度差;
(2)小球落地时的速度大小,以及速度与水平方向夹角。
Y :
X:
速度的大小
如图所示,水平屋顶高H=5m,墙高h=3.2m,墙到房子的距离L=3m,墙外马路宽x=10m,小球从房顶a点水平飞出,(取g=10m/s2)
(1)若小球落在墙外的马路上,求小球在空中运动的时间;
(2)若小球恰好经过墙顶b点后落在马路上,求小球离开房顶时的速度v0
(3)若小球落在墙外的马路上,求小球离开房顶时的速度v0的取值范围
Y :
X:
带角度θ计算步骤
Y :
X:
①
②
通过角度把XY两个方向的位移或速度进行几何关系(或三角函数)联系。
③
a.画出水平位移和竖直位移,找角度关系;
b.画出水平速度和竖直速度,找角度关系。
PS:速度偏转角关键字——恰好、相切、垂直
如图,从倾角θ的斜面顶端以初速度v0水平抛出小球,小球落在斜面上,求:
(1)小球空中飞行的时间;
(2)小球落点与抛出点间的距离。
v0
θ
小球以15m/s的水平速度抛向倾角37°的斜面,飞行一段时间后,恰好垂直撞到斜面上,g=10m/s2,求:
(1)小球空中飞行的时间;
(2)小球落点与抛出点间的高度。
v0
小球以水平速度v0抛出,飞行一段时间后,恰好不和挡板碰撞,重力加速度g,求小球运动轨迹与挡板M相距最近时对应的运动时间。
v0
M
θ
如图,平台顶端以初速度v0=8m/s水平抛出小球,恰好落在平台前倾角θ=37°的斜面顶端,并刚好沿着斜面下滑,已知平台高度与斜坡A点竖直相距h1 = 1.8m,斜面高度h2=14.4m,小球与斜面动摩擦因素为0.5,g = 10m/s2,忽略空气。求:
(1)小球空中飞行的时间以及刚落到斜面的速度;
(2)小球从平台抛出运动到B点的时间。
v0
θ
A
B
o
解:(1)急救用品做平抛运动,在竖直方向上做自由落体运动,有
得
急救用品在水平方向上做匀速直线运动,在t时间内的水平位移
(2)设急救用品落在水平面上时竖直方向速度的大小为
急救用品落在水平面时,速度的大小
滑雪运动员以20m/s的水平速度从一山坡飞出,问经过多长时间又落到斜坡上。已知斜坡与水平面成45°角落,取g=10m/s2。
x
y
450
A
B
解:滑雪运动可视为做平抛运动,如图,设经时间t落到斜坡上,有
由几何关系
即 y=x
得
练习
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
