1.2 运动的合成与分解 课件-2022-2023学年高一下学期物理粤教版(2019)必修第二册(28页ppt)
文档属性
| 名称 | 1.2 运动的合成与分解 课件-2022-2023学年高一下学期物理粤教版(2019)必修第二册(28页ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 32.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-01-10 21:44:33 | ||
图片预览






文档简介
1.2 运动的合成与分解
运动的分析
【观察与思考】
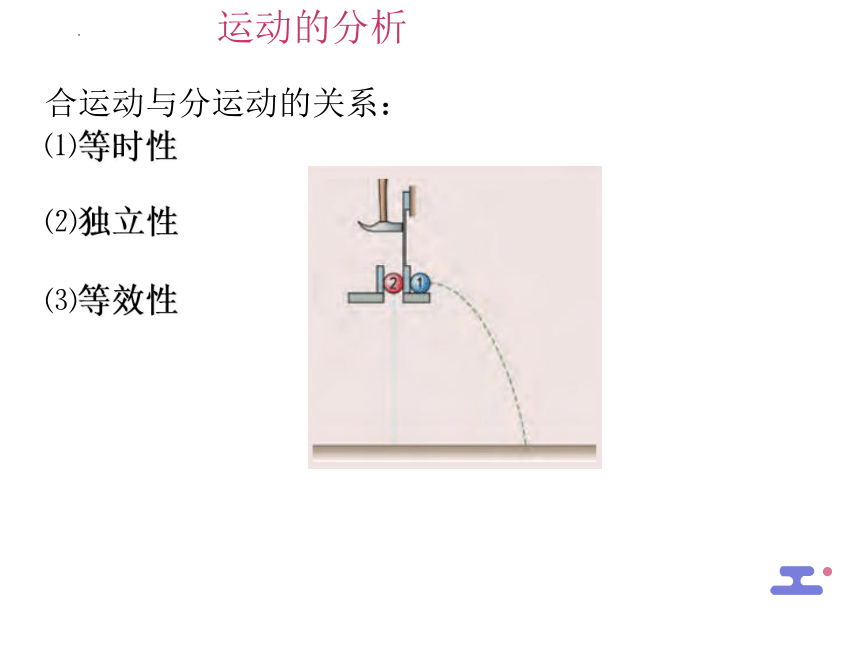
如右图,用小锤打击弹性金属片,球沿水平方向飞出。它的运动轨迹如何?
从运动产生的效果来看,合运动与分运动是一种什么关系?能否用自己的话把二者关系表达出来?
合运动
分运动
等效
替代
运动的分析
合运动与分运动
如果一个物体实际的运动效果跟另外两个运动的效果相同,把物体的实际运动叫做这两个运动的合运动,两个运动叫做这实际运动的分运动。
平抛与自由落体运动的等时性
合运动与分运动的关系:
⑴等时性
⑵独立性
⑶等效性
运动的分析
运动的合成和分解
二、速度和位移的合成与分解
“运动的合成与分解”包括:
s
s2
s1
v=s/t
v2=s2/t
v1=s1/t
物体的合运动(实际运动)速度叫合速度.
物体的合运动 (实际运动)位移叫合位移.
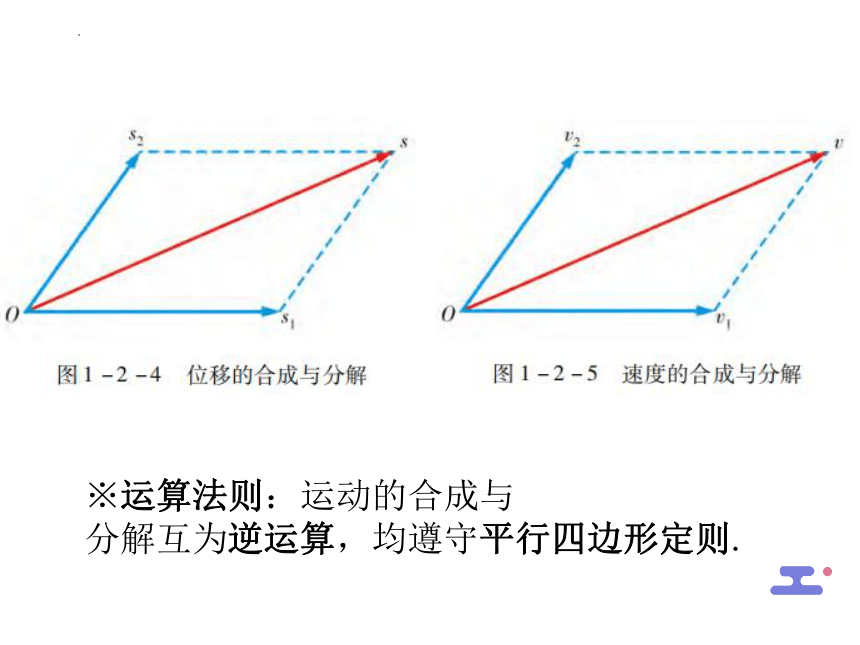
①位移的合成与分解
②速度的合成与分解
③加速度的合成与分解
※运算法则:运动的合成与
分解互为逆运算,均遵守平行四边形定则.
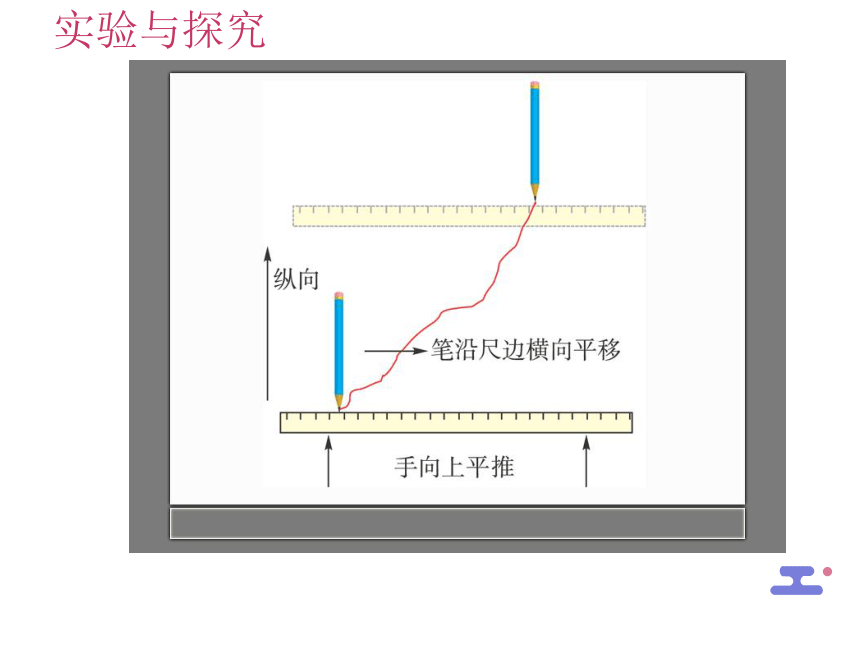
实验与探究
※运算法则:运动的合成与
分解互为逆运算,均遵守平行四边形定则.
小船过河:本质是合运动、分运动的思想
肉眼所见的速度是v合(实际速度)
三者速度关系满足平行四边形法则
v水:河流速度
v船:船在静水的速度
v合:船在动水的速度
分析1:时间最短
d
结论:欲使船渡河时间最短,船头的方向应该垂直于河岸。
解1:当船头垂直河岸时,所用时间最短
最短时间
此时航程
此时合速度
分析2:航程最短
θ
d
设船头指向与上游河岸成θ:
结论:当v船>v水时,最短航程等于河宽d。
????′=????22?????12
?
小船的速度
渡河所用的时间
船头方向与对岸的夹角
小船过河问题——合速度方向是实际运动的轨迹
设船在静水中的速度为v1,水流速v2,河宽为d
d
S1
S2
S
V2
V1
V
d
S1
S2
S
V2
V1
V
①最短时间:
d
tmin=d/v1
(船头⊥河岸)
② 最短位移:
α
当v1>v2时
V2
V1
V
S
α
当v1cosα=v2/v1
cosα=v1/v2
小船过河问题
设船在静水中的速度为v1,水流速v2,河宽为d
d
S1
S2
S
V2
V1
V
d
S1
S2
S
V2
V1
V
①最短时间:
tmin=d/v1
② 最短位移:(路线正对到达对岸)
α
当v1>v2时
cosα=v2/v1
????合=????12?????22
?
航程
对应时间
①船头⊥河岸
②船头与河岸成夹角
小船过河问题
设船在静水中的速度为v1,水流速v2,河宽为d
d
S1
S2
S
V2
V1
V
①最短时间:
d
tmin=d/v1
② 最短位移:(不能正对到达对岸)
V2
V1
V
S
α
当v1cosα=v1/v2
对应时间
????合=????22?????12
?
航程
三角函数
PS:以v船为半径,做相切圆求v合
①船头⊥河岸
②船头与河岸成夹角
一小船在静水中速度为3m/s,它在一条河宽为120m,水流速度为5m/s的河流中渡河,求:
(1)渡河的最短时间;
(2)渡河的最短位移。
d
② 最短位移:(不能正对到达对岸)
V2
V1
V
S
α
当v1cosα=v1/v2
对应时间
三角函数
关联速度——沿绳子、杆子、定滑轮
本质:合成与分解
现象:1.沿绳子、杆子方向速度大小相等;
2.垂直于接触面方向速度大小相等。
解决方法:
1.判断合运动(v合:肉眼所见的方向)方向;
2.分解合运动(v合)到绳或杆,沿绳做x轴,垂直于绳做y轴,建直角坐标系。
PS:
a.满足三角函数关系;
b.分清v绳、v合或v杆。
如图,人在岸边通过定滑轮用绳拉小船。人拉住绳子以速度v0匀速前进,当绳子与水平方向成θ角时,求小船的速度v。
拉船靠岸问题
v
v0
v2
匀速
沿绳做x轴,垂直于绳做y轴,建直角坐标系。
v1
v2
V1
v
θ
V1变大
例2:汽车以速度V匀速行驶,当汽车到达P点时,绳子与水平方向的夹角为θ,此时物体M的速度大小是多少?物体上升的速度随时间怎样变化的?
解:V1=Vcosθ
随时间θ减小
拉船问题
V1
V
P
M
产生a(向上)
绳子拉力大于M重力
B
如图,一条细绳跨过光滑轻定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直杆上。若B沿杆匀速下滑,速度为v,当绳与竖直杆间的夹角为θ时,则下列判断正确的是( )
D
B
B
运动的分析
【观察与思考】
如右图,用小锤打击弹性金属片,球沿水平方向飞出。它的运动轨迹如何?
从运动产生的效果来看,合运动与分运动是一种什么关系?能否用自己的话把二者关系表达出来?
合运动
分运动
等效
替代
运动的分析
合运动与分运动
如果一个物体实际的运动效果跟另外两个运动的效果相同,把物体的实际运动叫做这两个运动的合运动,两个运动叫做这实际运动的分运动。
平抛与自由落体运动的等时性
合运动与分运动的关系:
⑴等时性
⑵独立性
⑶等效性
运动的分析
运动的合成和分解
二、速度和位移的合成与分解
“运动的合成与分解”包括:
s
s2
s1
v=s/t
v2=s2/t
v1=s1/t
物体的合运动(实际运动)速度叫合速度.
物体的合运动 (实际运动)位移叫合位移.
①位移的合成与分解
②速度的合成与分解
③加速度的合成与分解
※运算法则:运动的合成与
分解互为逆运算,均遵守平行四边形定则.
实验与探究
※运算法则:运动的合成与
分解互为逆运算,均遵守平行四边形定则.
小船过河:本质是合运动、分运动的思想
肉眼所见的速度是v合(实际速度)
三者速度关系满足平行四边形法则
v水:河流速度
v船:船在静水的速度
v合:船在动水的速度
分析1:时间最短
d
结论:欲使船渡河时间最短,船头的方向应该垂直于河岸。
解1:当船头垂直河岸时,所用时间最短
最短时间
此时航程
此时合速度
分析2:航程最短
θ
d
设船头指向与上游河岸成θ:
结论:当v船>v水时,最短航程等于河宽d。
????′=????22?????12
?
小船的速度
渡河所用的时间
船头方向与对岸的夹角
小船过河问题——合速度方向是实际运动的轨迹
设船在静水中的速度为v1,水流速v2,河宽为d
d
S1
S2
S
V2
V1
V
d
S1
S2
S
V2
V1
V
①最短时间:
d
tmin=d/v1
(船头⊥河岸)
② 最短位移:
α
当v1>v2时
V2
V1
V
S
α
当v1
cosα=v1/v2
小船过河问题
设船在静水中的速度为v1,水流速v2,河宽为d
d
S1
S2
S
V2
V1
V
d
S1
S2
S
V2
V1
V
①最短时间:
tmin=d/v1
② 最短位移:(路线正对到达对岸)
α
当v1>v2时
cosα=v2/v1
????合=????12?????22
?
航程
对应时间
①船头⊥河岸
②船头与河岸成夹角
小船过河问题
设船在静水中的速度为v1,水流速v2,河宽为d
d
S1
S2
S
V2
V1
V
①最短时间:
d
tmin=d/v1
② 最短位移:(不能正对到达对岸)
V2
V1
V
S
α
当v1
对应时间
????合=????22?????12
?
航程
三角函数
PS:以v船为半径,做相切圆求v合
①船头⊥河岸
②船头与河岸成夹角
一小船在静水中速度为3m/s,它在一条河宽为120m,水流速度为5m/s的河流中渡河,求:
(1)渡河的最短时间;
(2)渡河的最短位移。
d
② 最短位移:(不能正对到达对岸)
V2
V1
V
S
α
当v1
对应时间
三角函数
关联速度——沿绳子、杆子、定滑轮
本质:合成与分解
现象:1.沿绳子、杆子方向速度大小相等;
2.垂直于接触面方向速度大小相等。
解决方法:
1.判断合运动(v合:肉眼所见的方向)方向;
2.分解合运动(v合)到绳或杆,沿绳做x轴,垂直于绳做y轴,建直角坐标系。
PS:
a.满足三角函数关系;
b.分清v绳、v合或v杆。
如图,人在岸边通过定滑轮用绳拉小船。人拉住绳子以速度v0匀速前进,当绳子与水平方向成θ角时,求小船的速度v。
拉船靠岸问题
v
v0
v2
匀速
沿绳做x轴,垂直于绳做y轴,建直角坐标系。
v1
v2
V1
v
θ
V1变大
例2:汽车以速度V匀速行驶,当汽车到达P点时,绳子与水平方向的夹角为θ,此时物体M的速度大小是多少?物体上升的速度随时间怎样变化的?
解:V1=Vcosθ
随时间θ减小
拉船问题
V1
V
P
M
产生a(向上)
绳子拉力大于M重力
B
如图,一条细绳跨过光滑轻定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直杆上。若B沿杆匀速下滑,速度为v,当绳与竖直杆间的夹角为θ时,则下列判断正确的是( )
D
B
B
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
