1.2 直角三角形(第一课时)课件(共19张PPT)
文档属性
| 名称 | 1.2 直角三角形(第一课时)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 817.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
主讲:XXX
1.2 直角三角形(第1课时)
北师大版八年级 下册
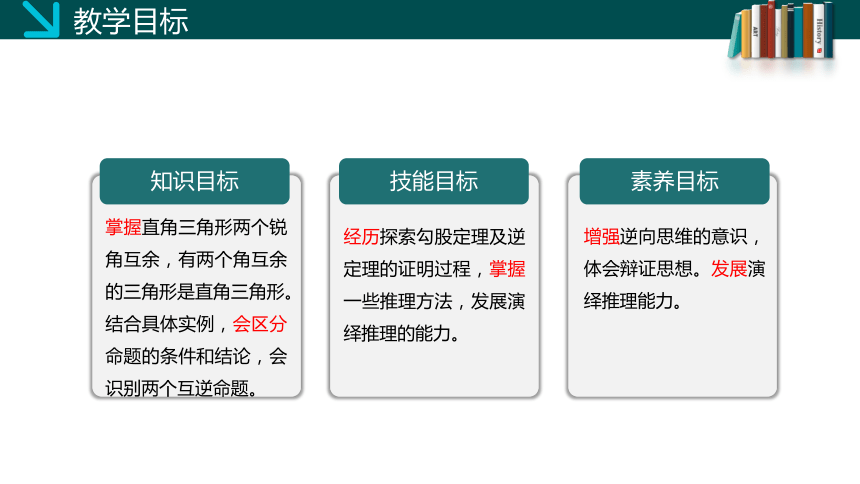
教学目标
素养目标
技能目标
知识目标
掌握直角三角形两个锐角互余,有两个角互余的三角形是直角三角形。结合具体实例,会区分命题的条件和结论,会识别两个互逆命题。
经历探索勾股定理及逆定理的证明过程,掌握一些推理方法,发展演绎推理的能力。
增强逆向思维的意识,体会辩证思想。发展演绎推理能力。
教学重难点
教学重点
教学难点
直角三角形中两个锐角的关系;勾股定理及逆定理的证明;识别逆命题和逆定理。
掌握推理证明的方法,发展演绎推理能力。
创设情境 引入新课
思考1:直角三角形的两个锐角有怎样的关系?为什么?
思考2:如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
请证明自己的结论,并与同伴交流.
直角三角形两个锐角互余。
有两个角互余的三角形是直角三角形。
典例探究 深化新知
条件:有两个角互余的三角形 已知:如图,在△ABC 中,∠A +∠B=90°
结论:是直角三角形 求证: △ABC是直角三角形。
定理 有两个角互余的三角形是直角三角形.
有两个角互余的三角形是直角三角形?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
数学符号语言如下:
归纳总结 认知升华
定理 有两个角互余的三角形是直角三角形
∵在△ABC 中,∠A +∠B=90°(已知)
∴△ABC是直角三角形。
典例探究 深化新知
思考4:反过来,在一个三角形中,当两边的平方和等于第三边
的平方时,我们曾用度量的方法得出“这个三角形是直
角三角形”的结论.你能用基本事实和已经学习过的定
理证明此结论吗?
思考3:我们前面曾利用数方格和割补图形的方法得到了勾股定理.
定理 直角三角形两条直角边的平方和等于斜边的平方。
其实我们也可以用基本事实和已经学习过的定理证明此结论,这里作为课后研读,P16读一读。
典例探究 深化新知
证明命题:如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形。
已知:如图,在△ABC 中,AC2 + BC2 = AB2.
求证:△ABC 是直角三角形.
证明:作Rt△DEF,使∠E=90°,DE=AC,FE=BC,
则DE2+EF2=DF2 (勾股定理).
∵AC2+BC2=AB2(已知), DE=AC,FE=BC (作图),
∴AB2=DF2,
∴AB=DF,
∴△ABC≌△DFE(SSS).
∴∠C=∠E=90°,
∴△ABC是直角三角形.
D
F
E
┏
A
B
C
定理 如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形。
数学符号语言如下:
归纳总结 认知升华
∵ 在△ABC 中,AC2 + BC2 = AB2(已知)
定理 如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形。
∴△ABC 是直角三角形.
巩固练习 拓展提高
判断下列三边组成的三角形是不是直角三角形.
(1)a = 2,b = 3,c = 4. ( )
(2)a = 9,b = 7,c = 12. ( )
(3)a = 25,b = 20,c = 15. ( )
×
×
√
典例探究 深化新知
观察上面两个命题,它们的条件和结论之间有怎样的关系?在前面的学习中还有类似的命题吗?
上面两个定理的条件和结论互换了位置,即勾股定理的条件是第二个定理的结论,结论是第二个定理的条件.
再观察下面三组命题:
如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
归纳总结 认知升华
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题.
上面每两个命题的条件和结论恰好互换了位置.
命题“两直线平行,内错角相等”的条件和结论为:
条件为:两直线平行;
结论为:内错角相等.
因此它的逆命题为:
内错角相等,两直线平行.
归纳总结 认知升华
每一个命题都有逆命题,只要将原命题的条件改成结论,并将结论改成条件,便可得到原命题的逆命题.但是原命题正确,它的逆命题未必正确.
例如真命题“对顶角相等”的逆命题为“相等的角是对顶角”,此命题就是假命题.
归纳总结 认知升华
如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.
注意1:逆命题、互逆命题不一定是真命题,
但逆定理、互逆定理,一定是真命题.
注意2:不是所有的定理都有逆定理.
巩固练习 拓展提高
1. 说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果 ab = 0,那么 a = 0,b = 0.
解:(1)多边形是四边形.原命题是真,逆命题是假.
(2)同旁内角互补,两直线平行.原命题是真,逆命题是真.
(3)如果那么 a = 0,b = 0,那么 ab = 0.原命题是假,逆命题是真.
归纳总结 认知升华
定理 直角三角形的两个锐角互余.
直角三角形
角的性质
边的性质
思想方法
定理 有两个角互余的三角形是直角三角形.
定理 直角三角形两条直角边的平方和等于斜边的平方.
定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
证明角度相等,线段相等利用全等三角形的性质来证明。
文字命题证明的四个特征:已知、求证、图形、证明。
分类讨论,逆向思维
文字语言-符号语言-图形语言的互相转化。
巩固练习 拓展提高
1. 一个零件的形状如图所示,工人师傅量得这个零件各边尺寸如下(单位:dm):AB = 3,AD = 4,BC = 12,CD = 13.且∠DAB = 90°.你能求出这个零件的面积吗?
解:如图,连接 BD. 在Rt△ABD 中,
在△BCD 中,
BD2 + BC2 = 52 + 122 = 132 = CD2.
∴△BCD 是直角三角形,∠DBC = 90°.
3
4
12
13
布置作业 减负增效
习题1.5第1、3题
行动是成功的阶梯,
行动越多,登得越高。
主讲:XXX
主讲:XXX
1.2 直角三角形(第1课时)
北师大版八年级 下册
教学目标
素养目标
技能目标
知识目标
掌握直角三角形两个锐角互余,有两个角互余的三角形是直角三角形。结合具体实例,会区分命题的条件和结论,会识别两个互逆命题。
经历探索勾股定理及逆定理的证明过程,掌握一些推理方法,发展演绎推理的能力。
增强逆向思维的意识,体会辩证思想。发展演绎推理能力。
教学重难点
教学重点
教学难点
直角三角形中两个锐角的关系;勾股定理及逆定理的证明;识别逆命题和逆定理。
掌握推理证明的方法,发展演绎推理能力。
创设情境 引入新课
思考1:直角三角形的两个锐角有怎样的关系?为什么?
思考2:如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
请证明自己的结论,并与同伴交流.
直角三角形两个锐角互余。
有两个角互余的三角形是直角三角形。
典例探究 深化新知
条件:有两个角互余的三角形 已知:如图,在△ABC 中,∠A +∠B=90°
结论:是直角三角形 求证: △ABC是直角三角形。
定理 有两个角互余的三角形是直角三角形.
有两个角互余的三角形是直角三角形?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
数学符号语言如下:
归纳总结 认知升华
定理 有两个角互余的三角形是直角三角形
∵在△ABC 中,∠A +∠B=90°(已知)
∴△ABC是直角三角形。
典例探究 深化新知
思考4:反过来,在一个三角形中,当两边的平方和等于第三边
的平方时,我们曾用度量的方法得出“这个三角形是直
角三角形”的结论.你能用基本事实和已经学习过的定
理证明此结论吗?
思考3:我们前面曾利用数方格和割补图形的方法得到了勾股定理.
定理 直角三角形两条直角边的平方和等于斜边的平方。
其实我们也可以用基本事实和已经学习过的定理证明此结论,这里作为课后研读,P16读一读。
典例探究 深化新知
证明命题:如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形。
已知:如图,在△ABC 中,AC2 + BC2 = AB2.
求证:△ABC 是直角三角形.
证明:作Rt△DEF,使∠E=90°,DE=AC,FE=BC,
则DE2+EF2=DF2 (勾股定理).
∵AC2+BC2=AB2(已知), DE=AC,FE=BC (作图),
∴AB2=DF2,
∴AB=DF,
∴△ABC≌△DFE(SSS).
∴∠C=∠E=90°,
∴△ABC是直角三角形.
D
F
E
┏
A
B
C
定理 如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形。
数学符号语言如下:
归纳总结 认知升华
∵ 在△ABC 中,AC2 + BC2 = AB2(已知)
定理 如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形。
∴△ABC 是直角三角形.
巩固练习 拓展提高
判断下列三边组成的三角形是不是直角三角形.
(1)a = 2,b = 3,c = 4. ( )
(2)a = 9,b = 7,c = 12. ( )
(3)a = 25,b = 20,c = 15. ( )
×
×
√
典例探究 深化新知
观察上面两个命题,它们的条件和结论之间有怎样的关系?在前面的学习中还有类似的命题吗?
上面两个定理的条件和结论互换了位置,即勾股定理的条件是第二个定理的结论,结论是第二个定理的条件.
再观察下面三组命题:
如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
归纳总结 认知升华
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题.
上面每两个命题的条件和结论恰好互换了位置.
命题“两直线平行,内错角相等”的条件和结论为:
条件为:两直线平行;
结论为:内错角相等.
因此它的逆命题为:
内错角相等,两直线平行.
归纳总结 认知升华
每一个命题都有逆命题,只要将原命题的条件改成结论,并将结论改成条件,便可得到原命题的逆命题.但是原命题正确,它的逆命题未必正确.
例如真命题“对顶角相等”的逆命题为“相等的角是对顶角”,此命题就是假命题.
归纳总结 认知升华
如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.
注意1:逆命题、互逆命题不一定是真命题,
但逆定理、互逆定理,一定是真命题.
注意2:不是所有的定理都有逆定理.
巩固练习 拓展提高
1. 说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;
(2)两直线平行,同旁内角互补;
(3)如果 ab = 0,那么 a = 0,b = 0.
解:(1)多边形是四边形.原命题是真,逆命题是假.
(2)同旁内角互补,两直线平行.原命题是真,逆命题是真.
(3)如果那么 a = 0,b = 0,那么 ab = 0.原命题是假,逆命题是真.
归纳总结 认知升华
定理 直角三角形的两个锐角互余.
直角三角形
角的性质
边的性质
思想方法
定理 有两个角互余的三角形是直角三角形.
定理 直角三角形两条直角边的平方和等于斜边的平方.
定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
证明角度相等,线段相等利用全等三角形的性质来证明。
文字命题证明的四个特征:已知、求证、图形、证明。
分类讨论,逆向思维
文字语言-符号语言-图形语言的互相转化。
巩固练习 拓展提高
1. 一个零件的形状如图所示,工人师傅量得这个零件各边尺寸如下(单位:dm):AB = 3,AD = 4,BC = 12,CD = 13.且∠DAB = 90°.你能求出这个零件的面积吗?
解:如图,连接 BD. 在Rt△ABD 中,
在△BCD 中,
BD2 + BC2 = 52 + 122 = 132 = CD2.
∴△BCD 是直角三角形,∠DBC = 90°.
3
4
12
13
布置作业 减负增效
习题1.5第1、3题
行动是成功的阶梯,
行动越多,登得越高。
主讲:XXX
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
