3.4.1 圆周角与圆心角的关系(1)课件(共28张PPT)
文档属性
| 名称 | 3.4.1 圆周角与圆心角的关系(1)课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 20:35:23 | ||
图片预览




文档简介
(共28张PPT)
3.4.1圆周角与圆心角的关系(1)
北师大版 九年级 下册
教学目标
教学目标:1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推论解决简
单的几何问题.
3.了解圆周角的分类,会推理验证“圆周角与圆心角的关系”.教学重点:理解圆周角与圆心角的关系并能运用圆周角定理及推论解决简单
的几何问题.
教学难点:了解圆周角的分类,会推理验证“圆周角与圆心角的关系”.
新知讲解
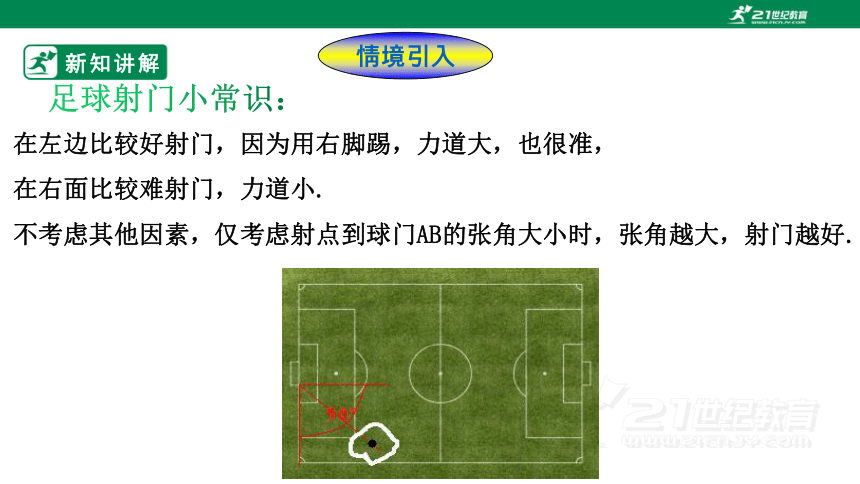
情境引入
足球射门小常识:
在左边比较好射门,因为用右脚踢,力道大,也很准,
在右面比较难射门,力道小.
不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.
合作学习
问题提出:当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC, ∠AEC.这三个角的大小有什么关系
B
A
C
D
E
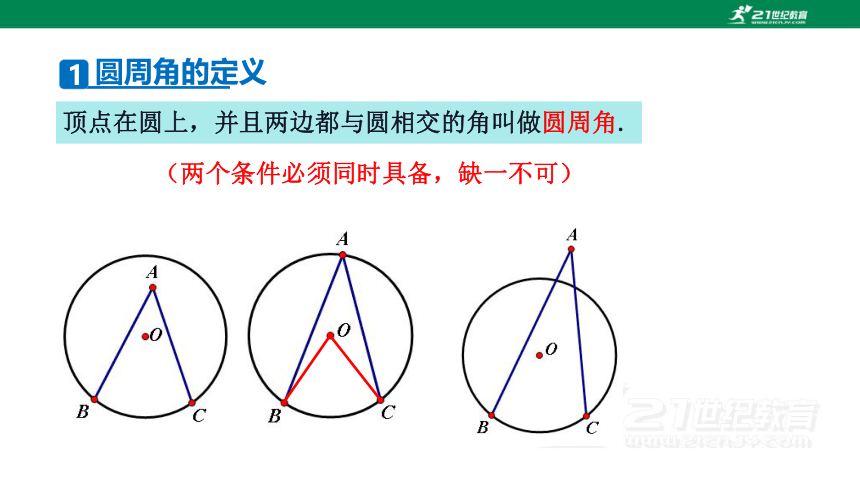
顶点在☉O上,角的两边分别与☉O相交.
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
圆周角的定义
1
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
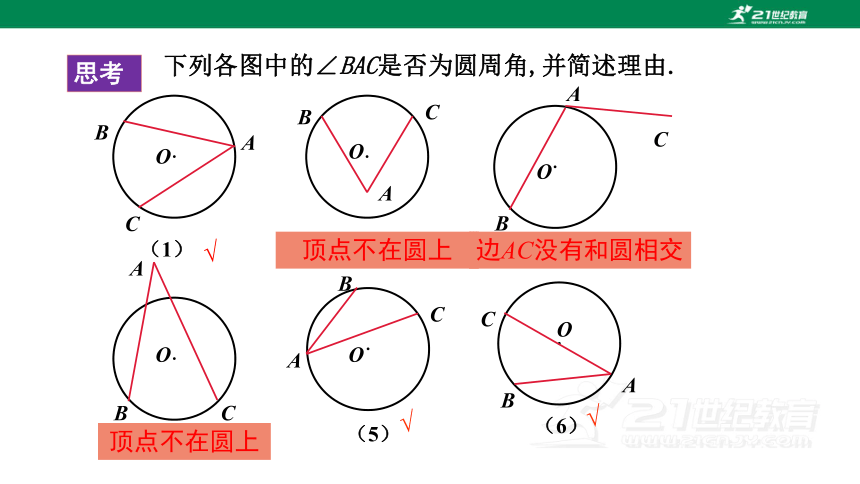
下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
思考
活动1: 圆周角与圆心角的关系
做一做:
如图,∠AOB=80°.
(1)请你画几个 所对的圆周角?这几个圆周角有什么关系?与同伴进行交流.
(2)这些圆周角和圆心角∠AOB的大小有什么关系?你是怎么发现的?与同伴进行交流.
D
E
F
∠D=∠E= ∠F=40°
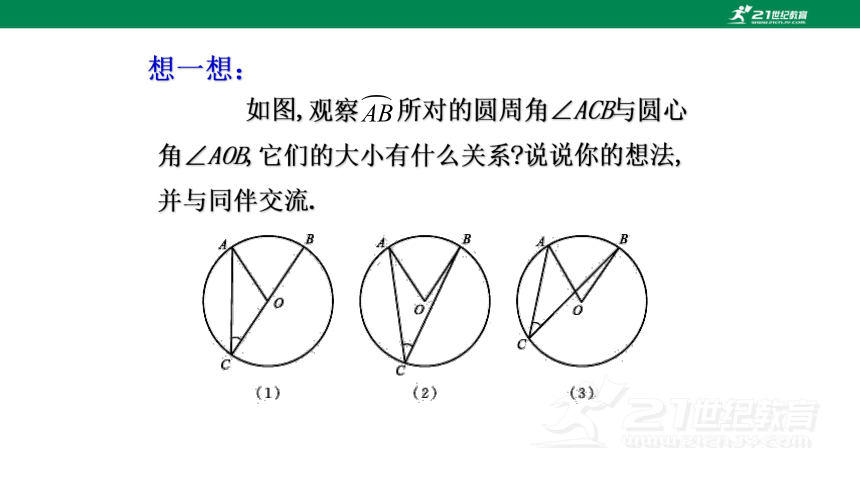
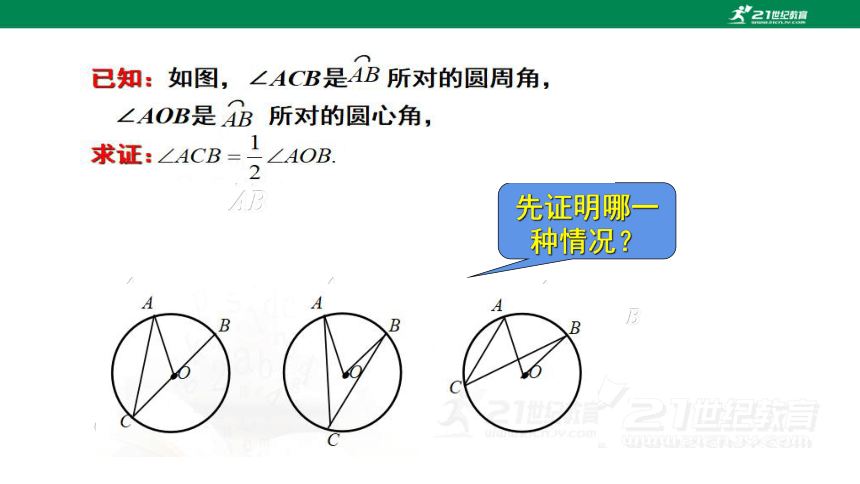
如图,观察 所对的圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系 说说你的想法,并与同伴交流.
想一想:
●O
A
C
B
●O
A
C
B
●O
A
C
B
AB
⌒
先证明哪一种情况?
AB
⌒
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ACB)的一边(BC)上时,
圆周角∠ACB与圆心角∠AOB的大小关系.
∵∠AOB是△ACO的外角,
∴∠AOB=∠C+∠A.
∵OA=OC,
∴∠A=∠C.
∴∠AOB=2∠C.
A
C
B
A
C
B
●O
2.当圆心(O)在圆周角(∠ACB)的内部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样
提示:能否转化为第一种情况
过点C作直径CD.由(1)可得:
●O
3.当圆心(O)在圆周角(∠ACB)的外部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样
提示:能否也转化为第一种情况
过点C作直径CD.由(1)可得:
A
C
B
提炼概念
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
圆周角定理
D
E
F
∠D=∠E= ∠F
典例精讲
例:如图:OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.
∠ACB与∠BAC的大小有什么关系?为什么?
证明:
∠ACB= ∠AOB
∠BAC= ∠BOC
∠AOB=2∠BOC
∠ACB=2∠BAC
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.
●
B
C
A
O
E
F
G
按从小到大的顺序
写出右图中BC弧所对的角∠A,∠E,∠O,∠F,∠G
< < < <
∠A
∠F
∠O
∠E
∠G
B
A
C
B
A
C
D
E
D
连接AO、CO,
问题回顾:当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角大小有什么关系
思考:如图,在⊙O中 = ,那么∠C和∠G的大小有什么关系 为什么
O
F
B
A
C
E
G
推论:同弧或等弧所对的圆周角相等
归纳概念
在同圆或等圆中,相等的弧(或同弧)
①所对的圆心角相等.
②所对的圆周角也相等并等于所对弧的圆心角的一半
在同圆或等圆中相等的圆周角所对的弧也相等.
课堂练习
1.如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为( )
A.84° B.60° C.36° D.24°
D
2.如图,点A、B、C、D在☉O上,点A与点D在点B、
C所在直线的同侧,∠BAC=35 .
(1)∠BOC= ,理由
是 ;
(2)∠BDC= ,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于该弧所对的圆心角的一半
3.为什么电影院的作为排列呈弧形,说一说这设计的合理性.
答:有些电影院的坐位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视角相等.
4.船在航行过程中,船长通过测定角度数来确定是否遇到暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系?
解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外) ,与两个灯塔的夹角∠α小于“危险角”.
5.如图,在⊙O 中,∠AOC=150°,求∠ABC,∠ADC 的度数,并判断∠ABC 和∠ADC,∠EBC 和∠ADC 之间的度数关系.
解题的关键是分清同弧所对的圆
心角和圆周角,如 所对的圆
心角是∠AOC,所对的圆周角是∠ABC,
所对的圆心角是大于平角的∠α,所对的圆周
角是∠ADC.
导引:
∵∠AOC=150°,∴∠ABC= ∠AOC=75°.
∵∠α=360°-∠AOC=360°-150°=210°,
∴∠ADC= ∠α=105°.
∵∠EBC=180°-∠ABC=180°-75°=105°,
∴∠EBC=∠ADC,即∠EBC 与∠ADC 相等.
又∵∠ABC+∠ADC=75°+105°=180°,
∴∠ABC 和∠ADC 互补.
解:
课堂总结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论1
圆周角的度数等于它所对弧上的圆心角度数的一半.
同弧或等弧所对的圆周角相等;
1.顶点在圆上,2.两边都与圆相交的角
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4.1圆周角与圆心角的关系(1)
北师大版 九年级 下册
教学目标
教学目标:1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推论解决简
单的几何问题.
3.了解圆周角的分类,会推理验证“圆周角与圆心角的关系”.教学重点:理解圆周角与圆心角的关系并能运用圆周角定理及推论解决简单
的几何问题.
教学难点:了解圆周角的分类,会推理验证“圆周角与圆心角的关系”.
新知讲解
情境引入
足球射门小常识:
在左边比较好射门,因为用右脚踢,力道大,也很准,
在右面比较难射门,力道小.
不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.
合作学习
问题提出:当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC, ∠AEC.这三个角的大小有什么关系
B
A
C
D
E
顶点在☉O上,角的两边分别与☉O相交.
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
圆周角的定义
1
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
思考
活动1: 圆周角与圆心角的关系
做一做:
如图,∠AOB=80°.
(1)请你画几个 所对的圆周角?这几个圆周角有什么关系?与同伴进行交流.
(2)这些圆周角和圆心角∠AOB的大小有什么关系?你是怎么发现的?与同伴进行交流.
D
E
F
∠D=∠E= ∠F=40°
如图,观察 所对的圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系 说说你的想法,并与同伴交流.
想一想:
●O
A
C
B
●O
A
C
B
●O
A
C
B
AB
⌒
先证明哪一种情况?
AB
⌒
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ACB)的一边(BC)上时,
圆周角∠ACB与圆心角∠AOB的大小关系.
∵∠AOB是△ACO的外角,
∴∠AOB=∠C+∠A.
∵OA=OC,
∴∠A=∠C.
∴∠AOB=2∠C.
A
C
B
A
C
B
●O
2.当圆心(O)在圆周角(∠ACB)的内部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样
提示:能否转化为第一种情况
过点C作直径CD.由(1)可得:
●O
3.当圆心(O)在圆周角(∠ACB)的外部时,圆周角∠ACB与圆心角∠AOB的大小关系会怎样
提示:能否也转化为第一种情况
过点C作直径CD.由(1)可得:
A
C
B
提炼概念
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
圆周角定理
D
E
F
∠D=∠E= ∠F
典例精讲
例:如图:OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.
∠ACB与∠BAC的大小有什么关系?为什么?
证明:
∠ACB= ∠AOB
∠BAC= ∠BOC
∠AOB=2∠BOC
∠ACB=2∠BAC
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理.
●
B
C
A
O
E
F
G
按从小到大的顺序
写出右图中BC弧所对的角∠A,∠E,∠O,∠F,∠G
< < < <
∠A
∠F
∠O
∠E
∠G
B
A
C
B
A
C
D
E
D
连接AO、CO,
问题回顾:当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC.这三个角大小有什么关系
思考:如图,在⊙O中 = ,那么∠C和∠G的大小有什么关系 为什么
O
F
B
A
C
E
G
推论:同弧或等弧所对的圆周角相等
归纳概念
在同圆或等圆中,相等的弧(或同弧)
①所对的圆心角相等.
②所对的圆周角也相等并等于所对弧的圆心角的一半
在同圆或等圆中相等的圆周角所对的弧也相等.
课堂练习
1.如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为( )
A.84° B.60° C.36° D.24°
D
2.如图,点A、B、C、D在☉O上,点A与点D在点B、
C所在直线的同侧,∠BAC=35 .
(1)∠BOC= ,理由
是 ;
(2)∠BDC= ,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于该弧所对的圆心角的一半
3.为什么电影院的作为排列呈弧形,说一说这设计的合理性.
答:有些电影院的坐位排列呈圆弧形,这样设计的理由是尽量保证同排的观众视角相等.
4.船在航行过程中,船长通过测定角度数来确定是否遇到暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系?
解:当船位于安全区域时,即船位于暗礁区域外(即⊙O外) ,与两个灯塔的夹角∠α小于“危险角”.
5.如图,在⊙O 中,∠AOC=150°,求∠ABC,∠ADC 的度数,并判断∠ABC 和∠ADC,∠EBC 和∠ADC 之间的度数关系.
解题的关键是分清同弧所对的圆
心角和圆周角,如 所对的圆
心角是∠AOC,所对的圆周角是∠ABC,
所对的圆心角是大于平角的∠α,所对的圆周
角是∠ADC.
导引:
∵∠AOC=150°,∴∠ABC= ∠AOC=75°.
∵∠α=360°-∠AOC=360°-150°=210°,
∴∠ADC= ∠α=105°.
∵∠EBC=180°-∠ABC=180°-75°=105°,
∴∠EBC=∠ADC,即∠EBC 与∠ADC 相等.
又∵∠ABC+∠ADC=75°+105°=180°,
∴∠ABC 和∠ADC 互补.
解:
课堂总结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论1
圆周角的度数等于它所对弧上的圆心角度数的一半.
同弧或等弧所对的圆周角相等;
1.顶点在圆上,2.两边都与圆相交的角
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
