人教版物理选修二典型题:带电粒子在有界匀强磁场中的运动(直线边界)
文档属性
| 名称 | 人教版物理选修二典型题:带电粒子在有界匀强磁场中的运动(直线边界) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-01-13 14:09:06 | ||
图片预览




文档简介
人教版物理选修二典型题:带电粒子在有界匀强磁场中的运动(直线边界)
1.如图所示,在边界MN的右侧区域有方向垂直纸面向里磁感应强度为B的匀强磁场,一个不计重力的带电粒子.电量为+q,质量为m,以速度v垂直MN边界从a点进入,由b点射出.求:
(1)a、b两点间的距离;
(2)粒子在磁场中运动的时间。
情景特点:边界MN的右侧区域 磁感应强度为B的匀强磁场 不计重力的带电粒子
问题特点:两点间的距离 磁场中运动的时间
【详解】(1)由牛顿第二定律可得
qvB=
解得
R=
则ab的距为
d=2R=
(2)由运动学公式有
T=
得
T=
在磁场中运动的时间为
t=T=
带电粒子在磁场中做圆周运动的半径和周期
1.由qvB=m,可得r=.
2.由r=和T=,可得T=.带电粒子在匀强磁场中做匀速圆周运动的周期与轨道半径和运动速度无关.
1.圆中三角关系
(1)粒子速度的偏向角(φ)等于圆心角(α),即φ=α
(2)圆心角(α)等于弦切角(θ)2倍,即α=2θ(弦:圆上两点的连线,切:速度方向)
(3)相对的弦切角(θ)相等,与相邻的弦切角(θ′)互补,即θ+θ′=180°。
2.运动时间的确定
粒子在磁场中运动一周的时间为T,当粒子运动的圆弧所对应的圆心角为α时,其运动时间可由下式表示:
t=T(或t=T),t=(l为弧长)。
3.常见运动轨迹的确定
直线边界(进出磁场具有对称性,如图丙所示)。
变式一、变方向
2.如图所示,虚线上方的空间存在无限大、方向垂直纸面向里的匀强磁场,磁感应强度。一带负电粒子以的初速度,从磁场边界a点,以与边界夹角的方向射入。已知该粒子的比荷,不计粒子的重力。
(1)画出粒子在磁场中运动轨迹的示意图;
(2)求粒子在磁场中做匀速圆周运动的半径;
(3)求粒子在磁场中运动的时间。
【详解】(1)根据左手定则可判断出,粒子的运动轨迹如图
(2)由
得粒子在磁场中做匀速圆周运动的半径为
(3)由
得粒子在磁场中做匀速圆周运动的周期为
由图可知,圆心角为,则粒子在磁场中运动的时间为
变式二、变问题
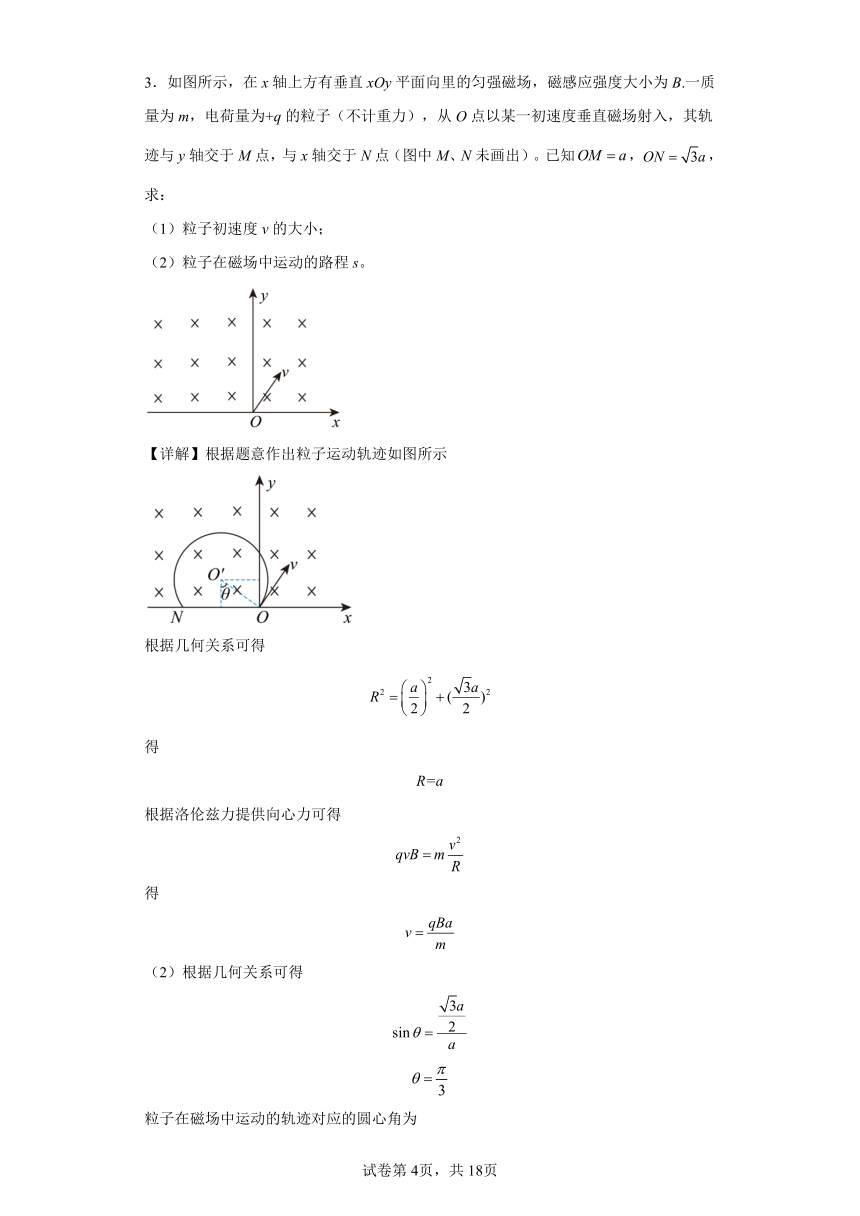
3.如图所示,在x轴上方有垂直xOy平面向里的匀强磁场,磁感应强度大小为B.一质量为m,电荷量为+q的粒子(不计重力),从O点以某一初速度垂直磁场射入,其轨迹与y轴交于M点,与x轴交于N点(图中M、N未画出)。已知,,求:
(1)粒子初速度v的大小;
(2)粒子在磁场中运动的路程s。
【详解】根据题意作出粒子运动轨迹如图所示
根据几何关系可得
得
R=a
根据洛伦兹力提供向心力可得
得
(2)根据几何关系可得
粒子在磁场中运动的轨迹对应的圆心角为
代入得
则粒子在磁场中运动的路程
代入得
变式三、变粒子
4.如图所示,直线上方有垂直纸面向外的匀强磁场,磁感应强度。两带有等量异种电荷的粒子,同时从点以相同速度射入磁场,速度方向与成角。已知粒子的质量均为,电荷量,不计粒子的重力及两粒子间相互作用力,求:
(1)它们从磁场中射出时相距多远?
(2)射出的时间差是多少?
【详解】(1)易知正、负电子偏转方向相反,做匀速圆周运动的半径相同,均设为r,根据牛顿第二定律有
解得
作出运动轨迹如图所示,根据几何关系可得它们从磁场中射出时相距
(2)正、负电子运动的周期均为
根据几何关系可知正、负电子转过的圆心角分别为60°和300°,所以射出的时间差是
5.如图所示,直线上方存在一足够大的方向垂直纸面向里的匀强磁场,一比荷为k的带负电粒子从O点沿与磁场边界成角的方向射入磁场中。已知磁场的磁感应强度大小为B,粒子在磁场中运动的过程中到磁场边界最远的距离为d,粒子重力不计,求:
(1)粒子射入磁场时速度的大小;
(2)粒子在磁场中运动的时间。
6.如图,直线MN上方有垂直纸面向里的足够大的有界匀强磁场区域,磁感应强度为B,一质量为m,电荷量为q(q<0)的带电粒子以速度v从O点射入该磁场区域,进入磁场时速度方向与MN边的夹角θ=60°,粒子在磁场中运动一段时间后从边界MN上的P点射出,粒子重力不计.求:
(1)带电粒子在磁场中运动的半径;
(2)入射点O与出射点P间的距离L;
(3)粒子在磁场中运动的时间t.
7.如图所示,直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点以与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电量为e),经一段时间后从边界MN射出.求:
(1)它们从磁场中射出时,出射点间的距离;
(2)它们从磁场中射出的时间差.
8.如图所示,直线MN上方存在着垂直纸面向里、磁感应强度为B的匀强磁场,一对质量为m、电荷量为e的正、负电子在纸面内以速度v0从O点同时射入磁场,其方向与MN的夹角;已知正、负电子分别从磁场边界的A、两点(图中未画出)离开磁场,不计粒子的重力及粒子间的相互作用。求:
(1)正、负电子在磁场边界上的穿出点A、之间的距离;
(2)正、负电子离开磁场的时间间隔。
9.水平直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从MN边界O点以与MN成300角的相同速度v射入该磁场区域(电子质量为m,电量为e)经一段时间后从边界MN射出,求:
(1)它们从磁场中射出时,出射点间的距离;(画出电子运动的轨迹图)
(2)它们从磁场中射出的时间差。
10.如图所示,直线MN上方为磁感应强度为B的足够大的匀强磁场。一电子(质量为m、电荷量为e)以v的速度从点O与MN成30°角的方向射入磁场中,求:
(1)电子在磁场中的半径多大;
(2)电子从磁场中射出时距O点多远;
(3)电子在磁场中运动的时间为多少.
11.如图所示,在虚线MN的上方存在磁感应强度为B的匀强磁场,方向垂直纸面向内,质子和粒子以相同的速度v0由MN上的O点以垂直MN且垂直于磁场的方向射入匀强磁场中,再分别从MN上A、B两点离开磁场.已知质子的质量为m,电荷为e,粒子的质量为4m,电荷为2e。忽略带电粒子的重力及质子和粒子间的相互作用。求:
(1)A、B两点间的距离;
(2)粒子在磁场中运动的时间。
12.如图所示,直线MN上方有垂直纸面向里的匀强磁场,磁感应强度为B,电子1从磁场边界上的a点垂直MN和磁场方向以速度v0射入磁场,从b点离开磁场,之后电子2也由a点沿图示方向以相同速率垂直磁场方向射入磁场,从a、b连线的中点c离开磁场。已知电子质量m,带电荷量为e,求:
(1)电子1在磁场中运动的半径r1;
(2)电子1在磁场中运动的时间t1;
(3)电子2在磁场中运动的时间t2。
13.如图所示,直线上方存在着垂直纸面向里、磁感应强度为的匀强磁场,质量为、电荷量为()的粒子1在纸面内以速度从点射入磁场,其方向与的夹角;质量为、电荷量为的粒子2在纸面内以速度也从点射入磁场,其方向与的夹角°。已知粒子1、2同时从磁场边界的进入磁场,不计粒子的重力及粒子间的相互作用。求:
(1)两粒子在磁场边界上的穿出点、之间的距离;
(2)两粒子射出磁场的时间间隔。
14.水平直线上方有垂直纸面向里的足够大的有界匀强磁场区域,磁感应强度为,有两个质量和电荷量均相同的正负粒子(不计重力)同时从边界点以与成角的相同速度射入该磁场区域(质量为,电量为q),正、负粒子间的相互作用忽略不计,经一段时间后从边界射出。
(1)分别画出正负粒子的运动轨迹,并指明哪个是负离子的轨迹。(保留作图痕迹,用黑色签字笔)
(2)求它们从磁场中射出时,出射点间的距离;
(3)求它们从磁场中射出的时间差。
15.水平直线上方有垂直纸面向里的足够大的有界匀强磁场区域,磁感应强度为,有两个质量和电荷量均相同的正负粒子(不计重力)同时从边界点以与成角的相同速度射入该磁场区域(质量为m,电量为e),正、负粒子间的相互作用忽略不计,经一段时间后从边界射出。
(1)求它们从磁场中射出时,出射点间的距离;
(2)求它们从磁场中射出的时间差。
5.(1);(2)
【详解】(1)带电粒子沿垂直于匀强磁场方向射入磁场,做匀速圆周运动,如图所示
洛伦兹力提供向心力,则有
由几何关系可知
联立解得
(2)由图可知,粒子在匀强磁场中运动轨迹的长度为
因粒子做匀速圆周运动,所以粒子在磁场中运动的时间为
联立解得
6.(1)(2) (3)
【详解】(1)粒子带负电,则粒子的运动轨迹如图;由
解得
(2)入射点O与出射点P间的距离
;
(3)粒子运动的周期
粒子在磁场中转过的角度为120°,则运动的时间
7.(1)(2)
【详解】(1)正、负电子在匀强磁场中圆周运动半径相同但绕行方向不同,分别作出正、负电子在磁场中运动的轨迹如图所示.
由得:
射出点距离为:PQ=4Rsinθ
所以:θ=30°
如图可知,两粒子离开时距O点均为R,所以出射点相距为:L=2R=
(2)由 得:
负电子在磁场中运动时间:
正电子在磁场中运动时间:
所以两个电子射出的时间差:△t=t1 t2=
点睛:带电粒子在电场中的运动关键在于由几何关系找出圆心和半径,再由洛仑兹力充当向心力及圆的性质可得出几何关系及转动时间.
8.(1);(2)
【详解】(1)电子在磁场中运动有
正电子的出射点A(在O点的左边)到O的距离即为其运动轨迹的弦长,即
同理可得,正电子的出射点B(在O点的右边)到O的距离即为其运动轨迹的弦长,即
则
联立解得
(2)电子在磁场中匀速圆周运动的周期为有
运动时间
正电子
负电子
则
联立可得
9.(1);(2)
【详解】(1)正、负电子在匀强磁场中圆周运动半径相同但绕行方向不同,分别作出正、负电子在磁场中运动的轨迹如图所示:
由
得
射出点距离
所以
(2)由
得
负电子在磁场中运动时间
正电子在磁场中运动时间
所以两个电子射出的时间差
10.(1);(2);(3)
【详解】(1)根据牛顿第二定律得
解得
(2)根据几何关系,圆心角为60°,电子从磁场中射出时距O点的距离为
(3)电子在磁场中运动的时间为
解得
11.(1)(2)
【详解】(1)质子进入磁场做半径为的匀速圆周运动,根据洛伦兹力提供向心力有
可得
质子离开磁场时到达A点,则O、A间的距离为
同理可得,α粒子在磁场中做圆周运动的半径为
α粒子离开磁场时到达B点,则O、B间的距离为
则A、B两点间的距离为
(2)α粒子在匀强磁场中运动周期为
则α粒子在磁场中运动的时间为
12.(1);(2);(3)
【详解】(1)电子1在磁场中运动时
得
(2)由得
电子1在磁场中转过了半圈,所用时间
(3)如图所示
两电子速率相等,半径相等,周期相同,设电子2在磁场中转过的圆心角为θ,则
则
θ=60°
所以
13.(1);(2)
【详解】(1)粒子在磁场中的运动轨迹如图所示
粒子在匀强磁场中,根据洛伦兹力提供向心力可得
可得粒子1、2在磁场运动轨迹半径分别为
,
由几何关系可得,粒子1、2射出点与O点的距离分别为
,
则、之间的距离为
(2)粒子做圆周运动的周期为
粒子1在磁场中运动的时间为
粒子2在磁场中运动的时间为
所以两粒子射出磁场的时间间隔为
14.(1);(2);(3)
【详解】(1)(2)正、负电子分别按逆、顺时针方向做匀速圆周运动(轨迹图)
则有
得
由几何关系
(2)由周期,正电子在磁场中运动时间
负电子在磁场中运动时间
它们从磁场中射出时间差
15.(1);(2)
【详解】(1)正、负电子分别按逆、顺时针方向做匀速圆周运动(轨迹图)
则有
得
由几何关系
(2)由周期
正电子在磁场中运动时间
负电子在磁场中运动时间
它们从磁场中射出时间差
一、题型特点分析
二、例题讲解
三、解题必备知识
四、方法总结
五、变式归纳
六、巩固练习
七、巩固练习参考答案
试卷第1页,共3页
试卷第1页,共3页
1.如图所示,在边界MN的右侧区域有方向垂直纸面向里磁感应强度为B的匀强磁场,一个不计重力的带电粒子.电量为+q,质量为m,以速度v垂直MN边界从a点进入,由b点射出.求:
(1)a、b两点间的距离;
(2)粒子在磁场中运动的时间。
情景特点:边界MN的右侧区域 磁感应强度为B的匀强磁场 不计重力的带电粒子
问题特点:两点间的距离 磁场中运动的时间
【详解】(1)由牛顿第二定律可得
qvB=
解得
R=
则ab的距为
d=2R=
(2)由运动学公式有
T=
得
T=
在磁场中运动的时间为
t=T=
带电粒子在磁场中做圆周运动的半径和周期
1.由qvB=m,可得r=.
2.由r=和T=,可得T=.带电粒子在匀强磁场中做匀速圆周运动的周期与轨道半径和运动速度无关.
1.圆中三角关系
(1)粒子速度的偏向角(φ)等于圆心角(α),即φ=α
(2)圆心角(α)等于弦切角(θ)2倍,即α=2θ(弦:圆上两点的连线,切:速度方向)
(3)相对的弦切角(θ)相等,与相邻的弦切角(θ′)互补,即θ+θ′=180°。
2.运动时间的确定
粒子在磁场中运动一周的时间为T,当粒子运动的圆弧所对应的圆心角为α时,其运动时间可由下式表示:
t=T(或t=T),t=(l为弧长)。
3.常见运动轨迹的确定
直线边界(进出磁场具有对称性,如图丙所示)。
变式一、变方向
2.如图所示,虚线上方的空间存在无限大、方向垂直纸面向里的匀强磁场,磁感应强度。一带负电粒子以的初速度,从磁场边界a点,以与边界夹角的方向射入。已知该粒子的比荷,不计粒子的重力。
(1)画出粒子在磁场中运动轨迹的示意图;
(2)求粒子在磁场中做匀速圆周运动的半径;
(3)求粒子在磁场中运动的时间。
【详解】(1)根据左手定则可判断出,粒子的运动轨迹如图
(2)由
得粒子在磁场中做匀速圆周运动的半径为
(3)由
得粒子在磁场中做匀速圆周运动的周期为
由图可知,圆心角为,则粒子在磁场中运动的时间为
变式二、变问题
3.如图所示,在x轴上方有垂直xOy平面向里的匀强磁场,磁感应强度大小为B.一质量为m,电荷量为+q的粒子(不计重力),从O点以某一初速度垂直磁场射入,其轨迹与y轴交于M点,与x轴交于N点(图中M、N未画出)。已知,,求:
(1)粒子初速度v的大小;
(2)粒子在磁场中运动的路程s。
【详解】根据题意作出粒子运动轨迹如图所示
根据几何关系可得
得
R=a
根据洛伦兹力提供向心力可得
得
(2)根据几何关系可得
粒子在磁场中运动的轨迹对应的圆心角为
代入得
则粒子在磁场中运动的路程
代入得
变式三、变粒子
4.如图所示,直线上方有垂直纸面向外的匀强磁场,磁感应强度。两带有等量异种电荷的粒子,同时从点以相同速度射入磁场,速度方向与成角。已知粒子的质量均为,电荷量,不计粒子的重力及两粒子间相互作用力,求:
(1)它们从磁场中射出时相距多远?
(2)射出的时间差是多少?
【详解】(1)易知正、负电子偏转方向相反,做匀速圆周运动的半径相同,均设为r,根据牛顿第二定律有
解得
作出运动轨迹如图所示,根据几何关系可得它们从磁场中射出时相距
(2)正、负电子运动的周期均为
根据几何关系可知正、负电子转过的圆心角分别为60°和300°,所以射出的时间差是
5.如图所示,直线上方存在一足够大的方向垂直纸面向里的匀强磁场,一比荷为k的带负电粒子从O点沿与磁场边界成角的方向射入磁场中。已知磁场的磁感应强度大小为B,粒子在磁场中运动的过程中到磁场边界最远的距离为d,粒子重力不计,求:
(1)粒子射入磁场时速度的大小;
(2)粒子在磁场中运动的时间。
6.如图,直线MN上方有垂直纸面向里的足够大的有界匀强磁场区域,磁感应强度为B,一质量为m,电荷量为q(q<0)的带电粒子以速度v从O点射入该磁场区域,进入磁场时速度方向与MN边的夹角θ=60°,粒子在磁场中运动一段时间后从边界MN上的P点射出,粒子重力不计.求:
(1)带电粒子在磁场中运动的半径;
(2)入射点O与出射点P间的距离L;
(3)粒子在磁场中运动的时间t.
7.如图所示,直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点以与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电量为e),经一段时间后从边界MN射出.求:
(1)它们从磁场中射出时,出射点间的距离;
(2)它们从磁场中射出的时间差.
8.如图所示,直线MN上方存在着垂直纸面向里、磁感应强度为B的匀强磁场,一对质量为m、电荷量为e的正、负电子在纸面内以速度v0从O点同时射入磁场,其方向与MN的夹角;已知正、负电子分别从磁场边界的A、两点(图中未画出)离开磁场,不计粒子的重力及粒子间的相互作用。求:
(1)正、负电子在磁场边界上的穿出点A、之间的距离;
(2)正、负电子离开磁场的时间间隔。
9.水平直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从MN边界O点以与MN成300角的相同速度v射入该磁场区域(电子质量为m,电量为e)经一段时间后从边界MN射出,求:
(1)它们从磁场中射出时,出射点间的距离;(画出电子运动的轨迹图)
(2)它们从磁场中射出的时间差。
10.如图所示,直线MN上方为磁感应强度为B的足够大的匀强磁场。一电子(质量为m、电荷量为e)以v的速度从点O与MN成30°角的方向射入磁场中,求:
(1)电子在磁场中的半径多大;
(2)电子从磁场中射出时距O点多远;
(3)电子在磁场中运动的时间为多少.
11.如图所示,在虚线MN的上方存在磁感应强度为B的匀强磁场,方向垂直纸面向内,质子和粒子以相同的速度v0由MN上的O点以垂直MN且垂直于磁场的方向射入匀强磁场中,再分别从MN上A、B两点离开磁场.已知质子的质量为m,电荷为e,粒子的质量为4m,电荷为2e。忽略带电粒子的重力及质子和粒子间的相互作用。求:
(1)A、B两点间的距离;
(2)粒子在磁场中运动的时间。
12.如图所示,直线MN上方有垂直纸面向里的匀强磁场,磁感应强度为B,电子1从磁场边界上的a点垂直MN和磁场方向以速度v0射入磁场,从b点离开磁场,之后电子2也由a点沿图示方向以相同速率垂直磁场方向射入磁场,从a、b连线的中点c离开磁场。已知电子质量m,带电荷量为e,求:
(1)电子1在磁场中运动的半径r1;
(2)电子1在磁场中运动的时间t1;
(3)电子2在磁场中运动的时间t2。
13.如图所示,直线上方存在着垂直纸面向里、磁感应强度为的匀强磁场,质量为、电荷量为()的粒子1在纸面内以速度从点射入磁场,其方向与的夹角;质量为、电荷量为的粒子2在纸面内以速度也从点射入磁场,其方向与的夹角°。已知粒子1、2同时从磁场边界的进入磁场,不计粒子的重力及粒子间的相互作用。求:
(1)两粒子在磁场边界上的穿出点、之间的距离;
(2)两粒子射出磁场的时间间隔。
14.水平直线上方有垂直纸面向里的足够大的有界匀强磁场区域,磁感应强度为,有两个质量和电荷量均相同的正负粒子(不计重力)同时从边界点以与成角的相同速度射入该磁场区域(质量为,电量为q),正、负粒子间的相互作用忽略不计,经一段时间后从边界射出。
(1)分别画出正负粒子的运动轨迹,并指明哪个是负离子的轨迹。(保留作图痕迹,用黑色签字笔)
(2)求它们从磁场中射出时,出射点间的距离;
(3)求它们从磁场中射出的时间差。
15.水平直线上方有垂直纸面向里的足够大的有界匀强磁场区域,磁感应强度为,有两个质量和电荷量均相同的正负粒子(不计重力)同时从边界点以与成角的相同速度射入该磁场区域(质量为m,电量为e),正、负粒子间的相互作用忽略不计,经一段时间后从边界射出。
(1)求它们从磁场中射出时,出射点间的距离;
(2)求它们从磁场中射出的时间差。
5.(1);(2)
【详解】(1)带电粒子沿垂直于匀强磁场方向射入磁场,做匀速圆周运动,如图所示
洛伦兹力提供向心力,则有
由几何关系可知
联立解得
(2)由图可知,粒子在匀强磁场中运动轨迹的长度为
因粒子做匀速圆周运动,所以粒子在磁场中运动的时间为
联立解得
6.(1)(2) (3)
【详解】(1)粒子带负电,则粒子的运动轨迹如图;由
解得
(2)入射点O与出射点P间的距离
;
(3)粒子运动的周期
粒子在磁场中转过的角度为120°,则运动的时间
7.(1)(2)
【详解】(1)正、负电子在匀强磁场中圆周运动半径相同但绕行方向不同,分别作出正、负电子在磁场中运动的轨迹如图所示.
由得:
射出点距离为:PQ=4Rsinθ
所以:θ=30°
如图可知,两粒子离开时距O点均为R,所以出射点相距为:L=2R=
(2)由 得:
负电子在磁场中运动时间:
正电子在磁场中运动时间:
所以两个电子射出的时间差:△t=t1 t2=
点睛:带电粒子在电场中的运动关键在于由几何关系找出圆心和半径,再由洛仑兹力充当向心力及圆的性质可得出几何关系及转动时间.
8.(1);(2)
【详解】(1)电子在磁场中运动有
正电子的出射点A(在O点的左边)到O的距离即为其运动轨迹的弦长,即
同理可得,正电子的出射点B(在O点的右边)到O的距离即为其运动轨迹的弦长,即
则
联立解得
(2)电子在磁场中匀速圆周运动的周期为有
运动时间
正电子
负电子
则
联立可得
9.(1);(2)
【详解】(1)正、负电子在匀强磁场中圆周运动半径相同但绕行方向不同,分别作出正、负电子在磁场中运动的轨迹如图所示:
由
得
射出点距离
所以
(2)由
得
负电子在磁场中运动时间
正电子在磁场中运动时间
所以两个电子射出的时间差
10.(1);(2);(3)
【详解】(1)根据牛顿第二定律得
解得
(2)根据几何关系,圆心角为60°,电子从磁场中射出时距O点的距离为
(3)电子在磁场中运动的时间为
解得
11.(1)(2)
【详解】(1)质子进入磁场做半径为的匀速圆周运动,根据洛伦兹力提供向心力有
可得
质子离开磁场时到达A点,则O、A间的距离为
同理可得,α粒子在磁场中做圆周运动的半径为
α粒子离开磁场时到达B点,则O、B间的距离为
则A、B两点间的距离为
(2)α粒子在匀强磁场中运动周期为
则α粒子在磁场中运动的时间为
12.(1);(2);(3)
【详解】(1)电子1在磁场中运动时
得
(2)由得
电子1在磁场中转过了半圈,所用时间
(3)如图所示
两电子速率相等,半径相等,周期相同,设电子2在磁场中转过的圆心角为θ,则
则
θ=60°
所以
13.(1);(2)
【详解】(1)粒子在磁场中的运动轨迹如图所示
粒子在匀强磁场中,根据洛伦兹力提供向心力可得
可得粒子1、2在磁场运动轨迹半径分别为
,
由几何关系可得,粒子1、2射出点与O点的距离分别为
,
则、之间的距离为
(2)粒子做圆周运动的周期为
粒子1在磁场中运动的时间为
粒子2在磁场中运动的时间为
所以两粒子射出磁场的时间间隔为
14.(1);(2);(3)
【详解】(1)(2)正、负电子分别按逆、顺时针方向做匀速圆周运动(轨迹图)
则有
得
由几何关系
(2)由周期,正电子在磁场中运动时间
负电子在磁场中运动时间
它们从磁场中射出时间差
15.(1);(2)
【详解】(1)正、负电子分别按逆、顺时针方向做匀速圆周运动(轨迹图)
则有
得
由几何关系
(2)由周期
正电子在磁场中运动时间
负电子在磁场中运动时间
它们从磁场中射出时间差
一、题型特点分析
二、例题讲解
三、解题必备知识
四、方法总结
五、变式归纳
六、巩固练习
七、巩固练习参考答案
试卷第1页,共3页
试卷第1页,共3页
