人教版物理选修二典型题:带电粒子在组合场中的运动
文档属性
| 名称 | 人教版物理选修二典型题:带电粒子在组合场中的运动 |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-01-13 14:09:06 | ||
图片预览



文档简介
人教版物理选修二典型题:带电粒子在组合场中的运动
1.电子自静止开始经电压为U的M,N板间的电场加速后从A 点垂直于磁场边界射入宽度为d、方向垂直纸面向里的匀强磁场中做匀速圆周运动,电子离开磁场时的速度方向与水平方向的夹角30°,如图所示。(已知电子的质量为m,电量为e)。求:
(1)电子进入磁场时的速度大小;
(2)求磁感应强度大小及电子在磁场中运动的时间。
(3)若改变磁场的大小,让电子恰好不从磁场右边界飞出,求此时的磁感应强度大小。
情景特点:电场加速 匀强磁场中做匀速圆周运动
问题特点:速度大小 运动的时间 磁感应强度大小
【详解】(1)电子在电场中被加速,则
解得
(2)由几何关系可知,电子在磁场中运动半径
根据
解得
电子在磁场中运动的周期
电子在磁场中运动的时间
(3)电子运动轨迹与磁场右边界相切时恰好不从右边界射出磁场,其轨道半径
r′=d
由牛顿第二定律得
解得
“电偏转”与“磁偏转”的比较
电偏转 磁偏转
偏转条件 只受恒定的电场力F=qEv⊥E进入匀强电场 只受大小恒定的洛伦兹力F=qvBv⊥B进入匀强磁场
运动轨迹 抛物线 INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-2.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "\\\\米昕\\e\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-2.tif" \* MERGEFORMATINET 圆弧 INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-3.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "\\\\米昕\\e\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-3.tif" \* MERGEFORMATINET
求解方法 利用类平抛运动的规律x=v0t,y=at2,a=,tan θ= 牛顿第二定律、向心力公式r=,T=,t=
带电粒子在电场、磁场组合场中的运动是指粒子从电场到磁场或从磁场到电场的运动.通常按时间的先后顺序分成若干个小过程,在每一运动过程中从粒子的受力性质、受力方向和速度方向的关系入手,分析粒子在电场中做什么运动,在磁场中做什么运动.
变式一、从电场进入磁场
2.电子由静止开始进入从M、N间的加速电场,经电压为U的电场加速后,从A点垂直于磁场边界射入宽度为d 的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.已知电子的质量为m,电量为e,求:
(1)电子进入磁场时的速度大小;
(2)匀强磁场的磁感应强度大小.
【详解】(1)根据动能定理,有
解得:
(2)电子进入磁场做匀速圆周运动,画出粒子运动的轨迹,如图所示
由几何关系得:
解得:
根据洛伦兹力提供向心力,有
得
变式二、从电场进入磁场
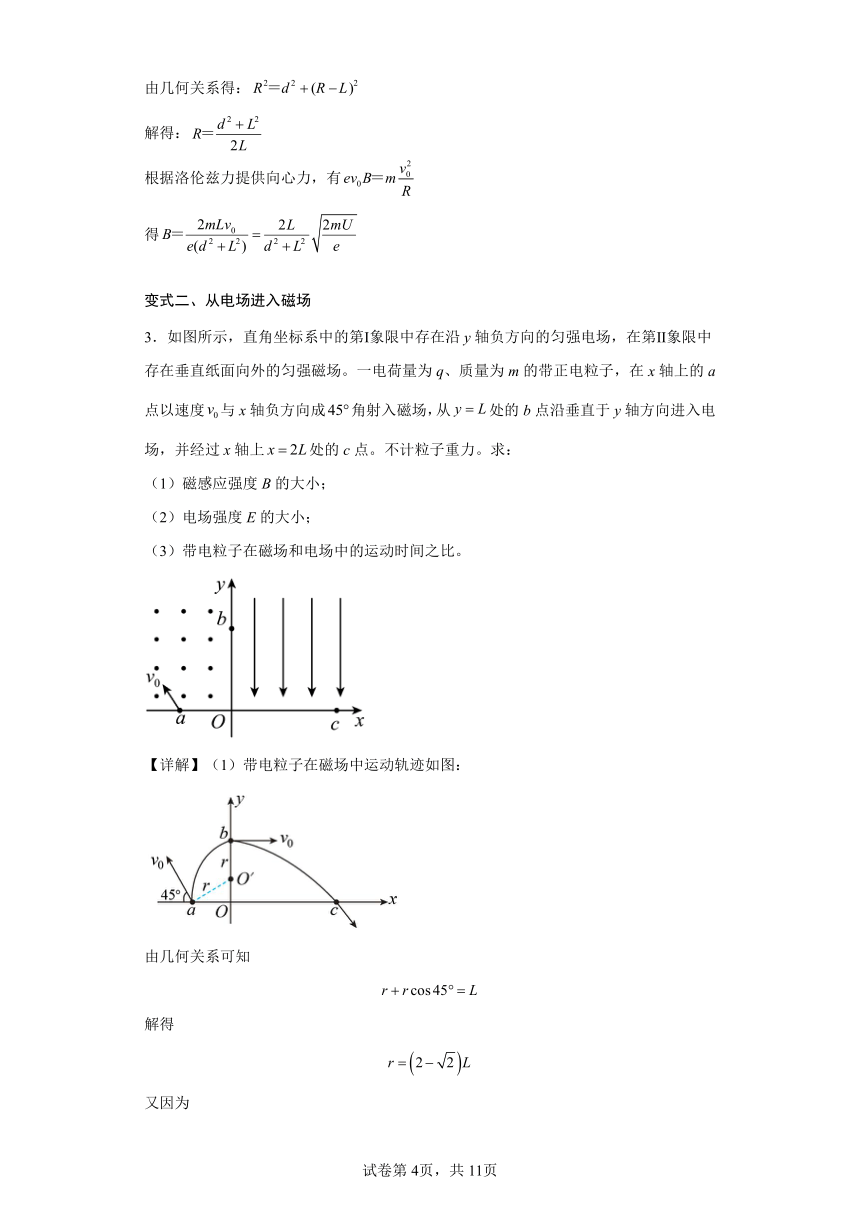
3.如图所示,直角坐标系中的第Ⅰ象限中存在沿y轴负方向的匀强电场,在第Ⅱ象限中存在垂直纸面向外的匀强磁场。一电荷量为q、质量为m的带正电粒子,在x轴上的a点以速度与x轴负方向成角射入磁场,从处的b点沿垂直于y轴方向进入电场,并经过x轴上处的c点。不计粒子重力。求:
(1)磁感应强度B的大小;
(2)电场强度E的大小;
(3)带电粒子在磁场和电场中的运动时间之比。
【详解】(1)带电粒子在磁场中运动轨迹如图:
由几何关系可知
解得
又因为
解得
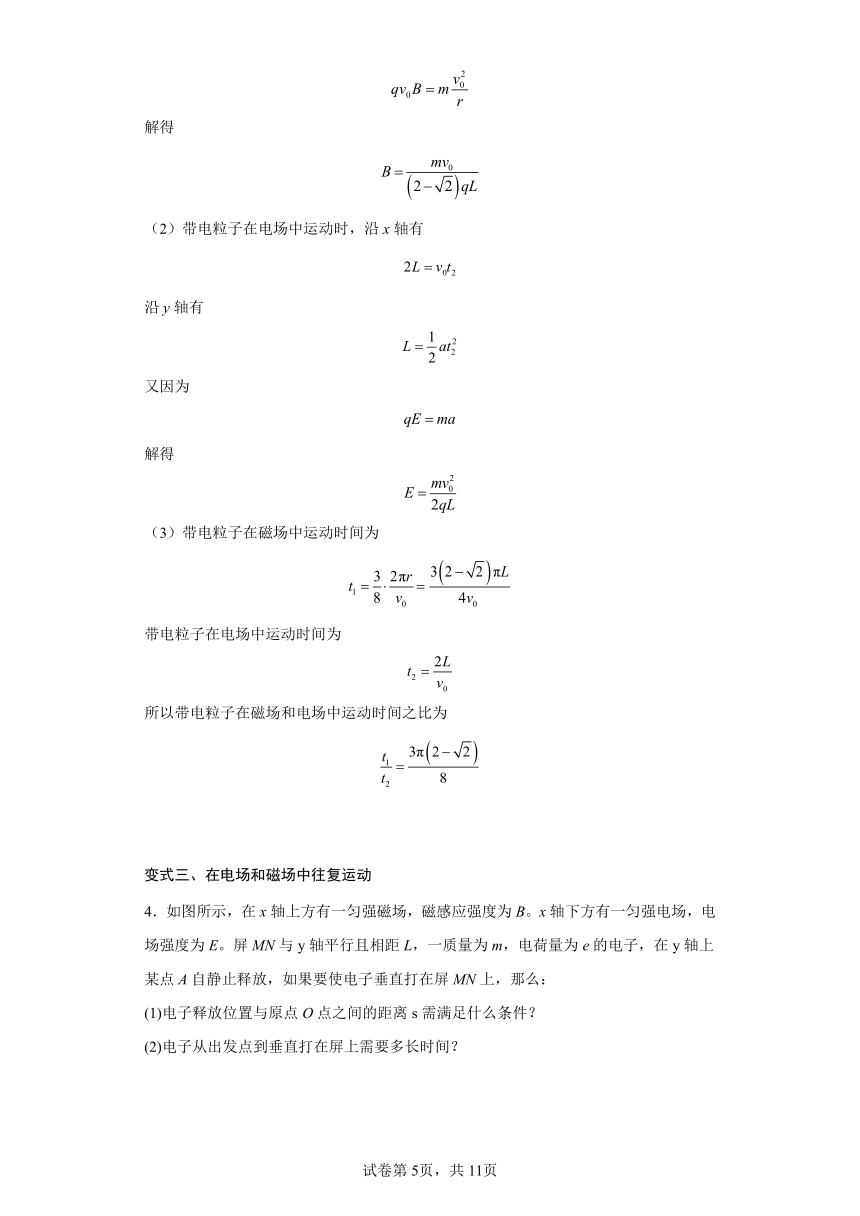
(2)带电粒子在电场中运动时,沿x轴有
沿y轴有
又因为
解得
(3)带电粒子在磁场中运动时间为
带电粒子在电场中运动时间为
所以带电粒子在磁场和电场中运动时间之比为
变式三、在电场和磁场中往复运动
4.如图所示,在x轴上方有一匀强磁场,磁感应强度为B。x轴下方有一匀强电场,电场强度为E。屏MN与y轴平行且相距L,一质量为m,电荷量为e的电子,在y轴上某点A自静止释放,如果要使电子垂直打在屏MN上,那么:
(1)电子释放位置与原点O点之间的距离s需满足什么条件?
(2)电子从出发点到垂直打在屏上需要多长时间?
【详解】(1)在电场中电子从A→O过程,由动能定理可得
在磁场中电子偏转,洛伦兹力提供向心力,有
可得
根据题意有
(2n+1)r=L
所以解得
(n=0,1,2,3…)
(2)电子在电场中做匀变速直线运动的时间与在磁场中做部分圆周运动的时间之和为电子运动的总时间,即
由公式 可得
由公式 和 可得
综上整理可得
(n=0,1,2,3…)
5.如图所示,在y>0的区域内有沿y轴正方向的匀强电场,在y<0的区域内有垂直于坐标平面向里的匀强磁场。一质量为m、电荷量为e的电子从y轴上A点以沿x轴正方向的初速度v0开始运动。当电子第一次穿越x轴时,恰好到达C点;当电子第二次穿越x轴时,恰好到达坐标原点;当电子第三次穿越x轴时,恰好到达D点。C、D两点均未在图中标出。已知A、C两点到坐标原点的距离分别为d、2d,不计电子的重力,求:
(1)电场强度E的大小;
(2)磁感应强度B的大小;
(3)电子从A运动到D经历的时间t。
6.如图所示,在y > 0的空间中存在匀强电场,场强沿y轴负方向;在y < 0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外。一电荷量为q、质量为m的带正电的运动粒子,经过y轴上y = h处的点P1时速率为v0,方向沿x轴正方向;然后,经过x轴上x = 2h处的P2点进入磁场,并经过y轴上y = - 2h的P3点。不计重力。求:
(1)电场强度的大小。
(2)粒子到达P2时速度的大小和方向。
(3)磁感应强度的大小。
7.如图所示,在坐标平面的第一象限内有一沿轴负方向的匀强电场,在第四象限内有一垂直于平面向外的匀强磁场,一质量为,带电量为的粒子(重力不计)经过电场中坐标为(,)的点时的速度大小为。方向沿轴负方向,然后以与轴负方向成角进入磁场,最后从坐标原点射出磁场,求:
(1)匀强电场的场强的大小;
(2)匀强磁场的磁感应强度的大小;
(3)粒子从点运动到原点所用的时间。
8.如图所示,一带电粒子质量为m、电荷量为q。从静止开始经电压为的电场加速后,水平进入两平行金属板间的偏转电场中,偏转电压为,接着进入一个方向垂直纸面向里、宽度为D的匀强磁场区域。已知偏转电场中金属板长为L,两板间距为d,带电粒子的重力忽略不计。求:
(1)带电微粒进入偏转电场时的速率;
(2)带电微粒射出偏转电场时的侧移量y;
(3)假设该带电粒子粒子出偏转电场的偏转角为,以速度垂直磁场方向进入匀强磁场,恰好没从右边界射出磁场,求该匀强磁场的磁感应强度B。
9.在如图所示的平面直角坐标系中,第二象限内存在磁感应强度为B1的匀强磁场,方向垂直于xOy平面向外;第一象限某矩形区域内存在磁感应强度B2=0.4T的匀强磁场,方向垂直于xOy平面向外。一个比荷为的带正电的粒子从点P(-10cm,0)发射进入第二象限,其速度,方向垂直于磁场B1且与x轴负方向夹角为30°;后从Q点以垂直y轴方向直接进入第一象限内的矩形磁场区域,再经M点以垂直x轴方向进入第四象限;整个第四象限存在大小、方向均未知的匀强电场,粒子经过该电场偏转后从N点进入无电场、磁场的第三象限区域,最终回到P点的速度与发射速度相同,不考虑粒子的重力。求:
(1)第二象限内磁场的磁感应强度B1的大小;
(2)粒子在矩形匀强磁场中的运动时间t和该磁场区域的最小面积S;
(3)第四象限内匀强电场场强E的大小。
10.如图所示,有界匀强磁场的磁感应强度B=2×10-3T:磁场右边是宽度L=0.2m、场强E=40V/m、方向向左的匀强电场,一带电粒子电荷量为q=3.2×10-19C的负电荷,质量m=6.4×10-27kg,以v=4×104m/s的速度沿OO′垂直射入磁场,在磁场中偏转后进入右侧的电场,最后从电场右边界射出,求:
(1)大致画出带电粒子的运动轨迹(画在题图L);
(2)带电粒子在磁场中运动的轨道半径;
(3)带电粒子飞出电场时的动能。
11.如图所示的坐标系xOy中,第一象限内存在垂直纸面向里的匀强磁场,磁感应强度为B0,第二象限存在沿y轴负方向的匀强电场,x轴下方存在垂直纸面向里的匀强磁场,磁感应强度未知。一带正电粒子从A(d,0)点以初速度v0开始运动,初速度方向与x轴负方向夹角θ=,粒子到达y轴时速度方向与y轴垂直,粒子经过电场区域、x轴下方磁场区域恰好回到A点,且速度方向与初速度方向相同。粒子重力不计,sin=0.8,cos=0.6,求:
(1)粒子的比荷;
(2)匀强电场的电场强度;
(3)x轴下方磁场的磁感应强度B。
12.如图所示,直角坐标系中的第Ⅰ象限中存在沿y轴负方向的匀强电场,在第Ⅱ象限中存在垂直纸面向外的匀强磁场.一电量为q、质量为m的带正电的粒子,在-x轴上的点a以速率v0,方向和-x轴方向成60°射入磁场,然后经过y轴上的b点垂直于y轴方向进入电场,并经过x轴上x=2L处的c点时速度大小为 v0.不计粒子重力.求
(1)磁感应强度B的大小
(2)电场强度E的大小.
13.如图所示的区域中,OM左边为垂直纸面向里的匀强磁场,右边是一个电场强度大小未知的匀强电场,其方向平行于OM,且垂直于磁场方向.一个质量为m、电荷量为-q的带电粒子从小孔P以初速度V0沿垂直于磁场方向进入匀强磁场中,初速度方向与边界线的夹角θ=60°,粒子恰好从小孔C垂直于OC射入匀强电场,最后打在Q点,已知OC=L,OQ=2L,不计粒子的重力,求:
(1)磁感应强度B的大小;
(2)电场强度E的大小.
14.如图,直角坐标系xOy中,在第一象限内有沿y轴负方向的匀强电场;在第三、第四象限内分别有方向垂直于坐标平面向里和向外的匀强磁场。一质量为m、电荷量为q(q>0)的粒子从y轴上P点(0、h)以初速度v0垂直于y轴射入电场,再经x轴上的Q点沿与x轴正方向成45°角进入磁场。粒子重力不计。
(1)求匀强电场的场强大小E;
(2)要使粒子能够进入第三象限,求第四象限内磁感应强度B的大小范围;
(3)若第四象限内磁感应强度大小为,第三象限内磁感应强度大小为,且第三、第四象限的磁场在y=-L(L>2h)处存在一条与x轴平行的下边界MN(图中未画出),则要使粒子能够垂直边界MN飞出磁场,求L的可能取值。
15.如图所示,在x轴上方有一匀强磁场方向垂直纸面向里。在x轴下方有一匀强电场,方向竖直向上。一个质量为m、电荷量为q、重力不计的带正电粒子从y轴上的a点(0,h)处沿y轴正方向以初速度开始运动,一段时间后,粒子速度方向与x轴正方向成45°角进入电场,经过y轴上b点时速度方向恰好与y轴垂直。求:
(1)匀强磁场的磁感应强度大小;
(2)匀强电场的电场强度大小;
(3)粒子从开始运动到第三次经过x轴的时间。
5.(1);(2);(3)
【详解】(1)电子的运动轨迹如图所示
电子在电场中做类平抛运动,设电子从A运动到C的时间为t1,有
2d=v0t1
d=a
a=
解得
E=
(2)设电子进入磁场时速度为v,v与x轴的夹角为θ,则
tan θ==1
解得
θ=45°
故
v=v0
电子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力,有
evB=m
由几何关系可知
r=d
解得
B=
(3)由对称性可知,电子在电场中运动的时间为
3t1=
电子在磁场中运动的时间
t2=T=
故电子从A运动到D的时间
t=3t1+t2=
6.(1);(2),方向与x轴夹角45°,斜向右下方;(3)
【分析】(1)粒子在电场中做类平抛运动,利用类平抛运动的位移公式结合牛顿第二定律可以求出电场强度的大小;
(2)粒子在磁场中做匀速圆周运动,利用速度的合成可以求出合速度的大小,利用运动的轨迹可以判别速度的方向;
(3)粒子在磁场中做匀速圆周运动,利用牛顿第二定律结合轨道半径的大小可以求出磁感应强度的大小。
【详解】(1)粒子在电场和磁场中的运动轨迹如图所示
设粒子从P1运动到P2的时间为t,电场强度的大小为E,粒子在电场中的加速度为a,由牛顿第二定律
qE = ma
根据运动学公式有
v0t = 2h
h = at2
联立以上解得
(2)粒子到达P2时速度沿x方向速度分量为v0,以v1为速度沿y方向速度分量的大小,v表示速度的大小,θ为速度与x轴的夹角,则有
由图可得
θ = 45°
有
v1 = v0
联立以上各式解得
方向与x轴夹角45°,斜向右下方。
(3)设磁场的磁感应强度为B,在洛伦兹力作用下粒子做匀速圆周运动,由牛顿第二定律可得
r是圆周的半径,与x轴、y轴的交点为P2、P3,因为
OP2 = OP3
θ = 45°
由几何关系可知,连线P2P3为圆周的直径,由几何关系可求得
联立解得
7.(1);(2);(3)
【详解】(1)粒子在电场中和磁场中的轨迹如图所示
设粒子进入磁场的速度大小为,根据题意有
粒子在电场中,根据动能定理可得
解得电场强度大小为
(2)粒子在匀强电场中做类平抛运动,沿方向做匀速直线运动,则有
沿方向有
可得
设粒子在磁场中的轨迹半径为,根据几何关系可得
粒子在磁场中由洛伦兹力提供向心力
联立解得
(3)粒子在电场中所用时间为
粒子在磁场中所用时间为
则粒子从点运动到原点所用的时间为
8.(1);(2);(3)
【详解】(1)带电微粒经加速电场加速后速度为 ,根据动能定理
解得
(2)射出偏转电场时
加速度为
联立解得侧移量为
(3)恰好没从右边界射出磁场,则其轨迹与右边界相切,根据几何关系
根据洛伦磁力提供向心力
解得
9.(1);(2) ;;(3)
【详解】
(1)如图由几何关系,粒子在第二象限圆周运动的半径为r1
①
洛伦兹力提供向心力
②
联立①②,解得
(2)粒子在第一象限中的运动
③
④
联立③④,解得
(3)粒子在第三象限中做匀速直线运动,如图NP连线方向与发射速度方向一致,则
设电场强度水平向左分量大小为Ex、竖直向上分量大小为Ey。对M→N过程
两个分场强矢量合成得
10.(1);(2)0.4m;(3)7.68×10-18J
【详解】(1)粒子运动轨边如图。
(2)带电粒子在磁场中运动时落仑兹力做向心力,则
得:=0.4m
(3)根据动能定理,粒子在射出电场过程中
代入数据解得:=7.68×10-18J
11.(1);(2);(3)
【详解】(1)设粒子在第一象限内做圆周运动的半径为r1,则有
由图中几何可知
解得
(2)设粒子平抛过程竖直位移为,则
由题意可知,粒子平抛运动的末速度与x轴负方向夹角
θ=
则
vy=v0tanθ
平抛运动过程
vy=at
联立解得
,
(3)设粒子平抛过程水平位移为,则,设粒子在y轴下方磁场区域运动的半径为r2,则
粒子运动速度
解得
12.(1) ;(2).
【详解】(1)设粒子在磁场中做圆周运动的轨道半径为r,Ob=y.
则有:y=t=t=L
粒子的运动轨迹如图所示:
由几何知识可得:r+rsin30°=y,
得:r= L
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
qv0B=m
解得:B=
(2)粒子在电场中做类平抛运动,到达c点时,竖直分速度为:
vy=
水平方向:2L=v0t,
竖直方向:vy=at
且有:
联立可得:
点睛:本题考查了粒子在磁场与电场中的运动,分析清楚粒子的运动过程、应用牛顿第二定律与类平抛运动规律、粒子做圆周运动的周期公式即可正确解题,解题时要注意数学知识的应用.
13.(1) (2)
【详解】(1)画出粒子运动的轨迹如图示 (O1为粒子在磁场中圆周运动的圆心): ∠PO1 C=120°
设粒子在磁场中圆周运动的半径为r,r+rcos 60°= OC=L
得r = 2L/3
粒子在磁场中圆周运动洛仑兹力充当向心力
解得
(2) 粒子在电场中类平抛运动,加速度为
由牛顿第二定律得
水平方向 2L=v0t
竖直方向
解得
14.(1);(2);(3)
【详解】(1)在第一象限内,粒子在电场力作用下做类平抛运动
由运动学规律有
,
由牛顿第二定律有:
联立解得
(2)粒子在点的速率
,
可得的距离为
粒子进入第四象限后做匀速圆周运动,如答图所示,轨迹恰与轴相切时,对应恰能够进入第三象限的磁感应强度最大值
由牛顿第二定律有
由几何关系有
联立以上各式解得
故的大小范围为
(3)由洛伦兹力提供向心力可知
粒子在第四、第三象限的轨道半径分别为
,
易知:粒子由点进入第四象限后运动半周进入第三象限,作出粒子在第四、第三象限的可能运动轨迹如答图所示
要让粒子垂直边界飞出磁场,则满足的条件为
结合题意
解得
15.(1);(2);(3)
【详解】(1)粒子运动轨迹如图
由图可得
rcos 45°=h
粒子在磁场中做圆周运动
联立可得
,
(2)粒子在x轴下方运动到 b点过程中,水平方向
竖直方向
由动能定理得
联立可得
,,
(3)粒子在磁场中运动总的圆心角
粒子在磁场中运动总的运动时间
粒子从开始运动到第三次经过x轴
t=t1+2t2
联立可得
一、题型特点分析
二、例题讲解
三、解题必备知识
四、方法总结
五、变式归纳
六、巩固练习
七、巩固练习参考答案
试卷第1页,共3页
试卷第1页,共3页
1.电子自静止开始经电压为U的M,N板间的电场加速后从A 点垂直于磁场边界射入宽度为d、方向垂直纸面向里的匀强磁场中做匀速圆周运动,电子离开磁场时的速度方向与水平方向的夹角30°,如图所示。(已知电子的质量为m,电量为e)。求:
(1)电子进入磁场时的速度大小;
(2)求磁感应强度大小及电子在磁场中运动的时间。
(3)若改变磁场的大小,让电子恰好不从磁场右边界飞出,求此时的磁感应强度大小。
情景特点:电场加速 匀强磁场中做匀速圆周运动
问题特点:速度大小 运动的时间 磁感应强度大小
【详解】(1)电子在电场中被加速,则
解得
(2)由几何关系可知,电子在磁场中运动半径
根据
解得
电子在磁场中运动的周期
电子在磁场中运动的时间
(3)电子运动轨迹与磁场右边界相切时恰好不从右边界射出磁场,其轨道半径
r′=d
由牛顿第二定律得
解得
“电偏转”与“磁偏转”的比较
电偏转 磁偏转
偏转条件 只受恒定的电场力F=qEv⊥E进入匀强电场 只受大小恒定的洛伦兹力F=qvBv⊥B进入匀强磁场
运动轨迹 抛物线 INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-2.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "\\\\米昕\\e\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-2.tif" \* MERGEFORMATINET 圆弧 INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-3.tif" \* MERGEFORMAT INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "F:\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "\\\\米昕\\e\\米昕\\2021\\同步\\物理 人教版 选择性必修第二册\\word\\59-3.tif" \* MERGEFORMATINET
求解方法 利用类平抛运动的规律x=v0t,y=at2,a=,tan θ= 牛顿第二定律、向心力公式r=,T=,t=
带电粒子在电场、磁场组合场中的运动是指粒子从电场到磁场或从磁场到电场的运动.通常按时间的先后顺序分成若干个小过程,在每一运动过程中从粒子的受力性质、受力方向和速度方向的关系入手,分析粒子在电场中做什么运动,在磁场中做什么运动.
变式一、从电场进入磁场
2.电子由静止开始进入从M、N间的加速电场,经电压为U的电场加速后,从A点垂直于磁场边界射入宽度为d 的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.已知电子的质量为m,电量为e,求:
(1)电子进入磁场时的速度大小;
(2)匀强磁场的磁感应强度大小.
【详解】(1)根据动能定理,有
解得:
(2)电子进入磁场做匀速圆周运动,画出粒子运动的轨迹,如图所示
由几何关系得:
解得:
根据洛伦兹力提供向心力,有
得
变式二、从电场进入磁场
3.如图所示,直角坐标系中的第Ⅰ象限中存在沿y轴负方向的匀强电场,在第Ⅱ象限中存在垂直纸面向外的匀强磁场。一电荷量为q、质量为m的带正电粒子,在x轴上的a点以速度与x轴负方向成角射入磁场,从处的b点沿垂直于y轴方向进入电场,并经过x轴上处的c点。不计粒子重力。求:
(1)磁感应强度B的大小;
(2)电场强度E的大小;
(3)带电粒子在磁场和电场中的运动时间之比。
【详解】(1)带电粒子在磁场中运动轨迹如图:
由几何关系可知
解得
又因为
解得
(2)带电粒子在电场中运动时,沿x轴有
沿y轴有
又因为
解得
(3)带电粒子在磁场中运动时间为
带电粒子在电场中运动时间为
所以带电粒子在磁场和电场中运动时间之比为
变式三、在电场和磁场中往复运动
4.如图所示,在x轴上方有一匀强磁场,磁感应强度为B。x轴下方有一匀强电场,电场强度为E。屏MN与y轴平行且相距L,一质量为m,电荷量为e的电子,在y轴上某点A自静止释放,如果要使电子垂直打在屏MN上,那么:
(1)电子释放位置与原点O点之间的距离s需满足什么条件?
(2)电子从出发点到垂直打在屏上需要多长时间?
【详解】(1)在电场中电子从A→O过程,由动能定理可得
在磁场中电子偏转,洛伦兹力提供向心力,有
可得
根据题意有
(2n+1)r=L
所以解得
(n=0,1,2,3…)
(2)电子在电场中做匀变速直线运动的时间与在磁场中做部分圆周运动的时间之和为电子运动的总时间,即
由公式 可得
由公式 和 可得
综上整理可得
(n=0,1,2,3…)
5.如图所示,在y>0的区域内有沿y轴正方向的匀强电场,在y<0的区域内有垂直于坐标平面向里的匀强磁场。一质量为m、电荷量为e的电子从y轴上A点以沿x轴正方向的初速度v0开始运动。当电子第一次穿越x轴时,恰好到达C点;当电子第二次穿越x轴时,恰好到达坐标原点;当电子第三次穿越x轴时,恰好到达D点。C、D两点均未在图中标出。已知A、C两点到坐标原点的距离分别为d、2d,不计电子的重力,求:
(1)电场强度E的大小;
(2)磁感应强度B的大小;
(3)电子从A运动到D经历的时间t。
6.如图所示,在y > 0的空间中存在匀强电场,场强沿y轴负方向;在y < 0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外。一电荷量为q、质量为m的带正电的运动粒子,经过y轴上y = h处的点P1时速率为v0,方向沿x轴正方向;然后,经过x轴上x = 2h处的P2点进入磁场,并经过y轴上y = - 2h的P3点。不计重力。求:
(1)电场强度的大小。
(2)粒子到达P2时速度的大小和方向。
(3)磁感应强度的大小。
7.如图所示,在坐标平面的第一象限内有一沿轴负方向的匀强电场,在第四象限内有一垂直于平面向外的匀强磁场,一质量为,带电量为的粒子(重力不计)经过电场中坐标为(,)的点时的速度大小为。方向沿轴负方向,然后以与轴负方向成角进入磁场,最后从坐标原点射出磁场,求:
(1)匀强电场的场强的大小;
(2)匀强磁场的磁感应强度的大小;
(3)粒子从点运动到原点所用的时间。
8.如图所示,一带电粒子质量为m、电荷量为q。从静止开始经电压为的电场加速后,水平进入两平行金属板间的偏转电场中,偏转电压为,接着进入一个方向垂直纸面向里、宽度为D的匀强磁场区域。已知偏转电场中金属板长为L,两板间距为d,带电粒子的重力忽略不计。求:
(1)带电微粒进入偏转电场时的速率;
(2)带电微粒射出偏转电场时的侧移量y;
(3)假设该带电粒子粒子出偏转电场的偏转角为,以速度垂直磁场方向进入匀强磁场,恰好没从右边界射出磁场,求该匀强磁场的磁感应强度B。
9.在如图所示的平面直角坐标系中,第二象限内存在磁感应强度为B1的匀强磁场,方向垂直于xOy平面向外;第一象限某矩形区域内存在磁感应强度B2=0.4T的匀强磁场,方向垂直于xOy平面向外。一个比荷为的带正电的粒子从点P(-10cm,0)发射进入第二象限,其速度,方向垂直于磁场B1且与x轴负方向夹角为30°;后从Q点以垂直y轴方向直接进入第一象限内的矩形磁场区域,再经M点以垂直x轴方向进入第四象限;整个第四象限存在大小、方向均未知的匀强电场,粒子经过该电场偏转后从N点进入无电场、磁场的第三象限区域,最终回到P点的速度与发射速度相同,不考虑粒子的重力。求:
(1)第二象限内磁场的磁感应强度B1的大小;
(2)粒子在矩形匀强磁场中的运动时间t和该磁场区域的最小面积S;
(3)第四象限内匀强电场场强E的大小。
10.如图所示,有界匀强磁场的磁感应强度B=2×10-3T:磁场右边是宽度L=0.2m、场强E=40V/m、方向向左的匀强电场,一带电粒子电荷量为q=3.2×10-19C的负电荷,质量m=6.4×10-27kg,以v=4×104m/s的速度沿OO′垂直射入磁场,在磁场中偏转后进入右侧的电场,最后从电场右边界射出,求:
(1)大致画出带电粒子的运动轨迹(画在题图L);
(2)带电粒子在磁场中运动的轨道半径;
(3)带电粒子飞出电场时的动能。
11.如图所示的坐标系xOy中,第一象限内存在垂直纸面向里的匀强磁场,磁感应强度为B0,第二象限存在沿y轴负方向的匀强电场,x轴下方存在垂直纸面向里的匀强磁场,磁感应强度未知。一带正电粒子从A(d,0)点以初速度v0开始运动,初速度方向与x轴负方向夹角θ=,粒子到达y轴时速度方向与y轴垂直,粒子经过电场区域、x轴下方磁场区域恰好回到A点,且速度方向与初速度方向相同。粒子重力不计,sin=0.8,cos=0.6,求:
(1)粒子的比荷;
(2)匀强电场的电场强度;
(3)x轴下方磁场的磁感应强度B。
12.如图所示,直角坐标系中的第Ⅰ象限中存在沿y轴负方向的匀强电场,在第Ⅱ象限中存在垂直纸面向外的匀强磁场.一电量为q、质量为m的带正电的粒子,在-x轴上的点a以速率v0,方向和-x轴方向成60°射入磁场,然后经过y轴上的b点垂直于y轴方向进入电场,并经过x轴上x=2L处的c点时速度大小为 v0.不计粒子重力.求
(1)磁感应强度B的大小
(2)电场强度E的大小.
13.如图所示的区域中,OM左边为垂直纸面向里的匀强磁场,右边是一个电场强度大小未知的匀强电场,其方向平行于OM,且垂直于磁场方向.一个质量为m、电荷量为-q的带电粒子从小孔P以初速度V0沿垂直于磁场方向进入匀强磁场中,初速度方向与边界线的夹角θ=60°,粒子恰好从小孔C垂直于OC射入匀强电场,最后打在Q点,已知OC=L,OQ=2L,不计粒子的重力,求:
(1)磁感应强度B的大小;
(2)电场强度E的大小.
14.如图,直角坐标系xOy中,在第一象限内有沿y轴负方向的匀强电场;在第三、第四象限内分别有方向垂直于坐标平面向里和向外的匀强磁场。一质量为m、电荷量为q(q>0)的粒子从y轴上P点(0、h)以初速度v0垂直于y轴射入电场,再经x轴上的Q点沿与x轴正方向成45°角进入磁场。粒子重力不计。
(1)求匀强电场的场强大小E;
(2)要使粒子能够进入第三象限,求第四象限内磁感应强度B的大小范围;
(3)若第四象限内磁感应强度大小为,第三象限内磁感应强度大小为,且第三、第四象限的磁场在y=-L(L>2h)处存在一条与x轴平行的下边界MN(图中未画出),则要使粒子能够垂直边界MN飞出磁场,求L的可能取值。
15.如图所示,在x轴上方有一匀强磁场方向垂直纸面向里。在x轴下方有一匀强电场,方向竖直向上。一个质量为m、电荷量为q、重力不计的带正电粒子从y轴上的a点(0,h)处沿y轴正方向以初速度开始运动,一段时间后,粒子速度方向与x轴正方向成45°角进入电场,经过y轴上b点时速度方向恰好与y轴垂直。求:
(1)匀强磁场的磁感应强度大小;
(2)匀强电场的电场强度大小;
(3)粒子从开始运动到第三次经过x轴的时间。
5.(1);(2);(3)
【详解】(1)电子的运动轨迹如图所示
电子在电场中做类平抛运动,设电子从A运动到C的时间为t1,有
2d=v0t1
d=a
a=
解得
E=
(2)设电子进入磁场时速度为v,v与x轴的夹角为θ,则
tan θ==1
解得
θ=45°
故
v=v0
电子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力,有
evB=m
由几何关系可知
r=d
解得
B=
(3)由对称性可知,电子在电场中运动的时间为
3t1=
电子在磁场中运动的时间
t2=T=
故电子从A运动到D的时间
t=3t1+t2=
6.(1);(2),方向与x轴夹角45°,斜向右下方;(3)
【分析】(1)粒子在电场中做类平抛运动,利用类平抛运动的位移公式结合牛顿第二定律可以求出电场强度的大小;
(2)粒子在磁场中做匀速圆周运动,利用速度的合成可以求出合速度的大小,利用运动的轨迹可以判别速度的方向;
(3)粒子在磁场中做匀速圆周运动,利用牛顿第二定律结合轨道半径的大小可以求出磁感应强度的大小。
【详解】(1)粒子在电场和磁场中的运动轨迹如图所示
设粒子从P1运动到P2的时间为t,电场强度的大小为E,粒子在电场中的加速度为a,由牛顿第二定律
qE = ma
根据运动学公式有
v0t = 2h
h = at2
联立以上解得
(2)粒子到达P2时速度沿x方向速度分量为v0,以v1为速度沿y方向速度分量的大小,v表示速度的大小,θ为速度与x轴的夹角,则有
由图可得
θ = 45°
有
v1 = v0
联立以上各式解得
方向与x轴夹角45°,斜向右下方。
(3)设磁场的磁感应强度为B,在洛伦兹力作用下粒子做匀速圆周运动,由牛顿第二定律可得
r是圆周的半径,与x轴、y轴的交点为P2、P3,因为
OP2 = OP3
θ = 45°
由几何关系可知,连线P2P3为圆周的直径,由几何关系可求得
联立解得
7.(1);(2);(3)
【详解】(1)粒子在电场中和磁场中的轨迹如图所示
设粒子进入磁场的速度大小为,根据题意有
粒子在电场中,根据动能定理可得
解得电场强度大小为
(2)粒子在匀强电场中做类平抛运动,沿方向做匀速直线运动,则有
沿方向有
可得
设粒子在磁场中的轨迹半径为,根据几何关系可得
粒子在磁场中由洛伦兹力提供向心力
联立解得
(3)粒子在电场中所用时间为
粒子在磁场中所用时间为
则粒子从点运动到原点所用的时间为
8.(1);(2);(3)
【详解】(1)带电微粒经加速电场加速后速度为 ,根据动能定理
解得
(2)射出偏转电场时
加速度为
联立解得侧移量为
(3)恰好没从右边界射出磁场,则其轨迹与右边界相切,根据几何关系
根据洛伦磁力提供向心力
解得
9.(1);(2) ;;(3)
【详解】
(1)如图由几何关系,粒子在第二象限圆周运动的半径为r1
①
洛伦兹力提供向心力
②
联立①②,解得
(2)粒子在第一象限中的运动
③
④
联立③④,解得
(3)粒子在第三象限中做匀速直线运动,如图NP连线方向与发射速度方向一致,则
设电场强度水平向左分量大小为Ex、竖直向上分量大小为Ey。对M→N过程
两个分场强矢量合成得
10.(1);(2)0.4m;(3)7.68×10-18J
【详解】(1)粒子运动轨边如图。
(2)带电粒子在磁场中运动时落仑兹力做向心力,则
得:=0.4m
(3)根据动能定理,粒子在射出电场过程中
代入数据解得:=7.68×10-18J
11.(1);(2);(3)
【详解】(1)设粒子在第一象限内做圆周运动的半径为r1,则有
由图中几何可知
解得
(2)设粒子平抛过程竖直位移为,则
由题意可知,粒子平抛运动的末速度与x轴负方向夹角
θ=
则
vy=v0tanθ
平抛运动过程
vy=at
联立解得
,
(3)设粒子平抛过程水平位移为,则,设粒子在y轴下方磁场区域运动的半径为r2,则
粒子运动速度
解得
12.(1) ;(2).
【详解】(1)设粒子在磁场中做圆周运动的轨道半径为r,Ob=y.
则有:y=t=t=L
粒子的运动轨迹如图所示:
由几何知识可得:r+rsin30°=y,
得:r= L
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
qv0B=m
解得:B=
(2)粒子在电场中做类平抛运动,到达c点时,竖直分速度为:
vy=
水平方向:2L=v0t,
竖直方向:vy=at
且有:
联立可得:
点睛:本题考查了粒子在磁场与电场中的运动,分析清楚粒子的运动过程、应用牛顿第二定律与类平抛运动规律、粒子做圆周运动的周期公式即可正确解题,解题时要注意数学知识的应用.
13.(1) (2)
【详解】(1)画出粒子运动的轨迹如图示 (O1为粒子在磁场中圆周运动的圆心): ∠PO1 C=120°
设粒子在磁场中圆周运动的半径为r,r+rcos 60°= OC=L
得r = 2L/3
粒子在磁场中圆周运动洛仑兹力充当向心力
解得
(2) 粒子在电场中类平抛运动,加速度为
由牛顿第二定律得
水平方向 2L=v0t
竖直方向
解得
14.(1);(2);(3)
【详解】(1)在第一象限内,粒子在电场力作用下做类平抛运动
由运动学规律有
,
由牛顿第二定律有:
联立解得
(2)粒子在点的速率
,
可得的距离为
粒子进入第四象限后做匀速圆周运动,如答图所示,轨迹恰与轴相切时,对应恰能够进入第三象限的磁感应强度最大值
由牛顿第二定律有
由几何关系有
联立以上各式解得
故的大小范围为
(3)由洛伦兹力提供向心力可知
粒子在第四、第三象限的轨道半径分别为
,
易知:粒子由点进入第四象限后运动半周进入第三象限,作出粒子在第四、第三象限的可能运动轨迹如答图所示
要让粒子垂直边界飞出磁场,则满足的条件为
结合题意
解得
15.(1);(2);(3)
【详解】(1)粒子运动轨迹如图
由图可得
rcos 45°=h
粒子在磁场中做圆周运动
联立可得
,
(2)粒子在x轴下方运动到 b点过程中,水平方向
竖直方向
由动能定理得
联立可得
,,
(3)粒子在磁场中运动总的圆心角
粒子在磁场中运动总的运动时间
粒子从开始运动到第三次经过x轴
t=t1+2t2
联立可得
一、题型特点分析
二、例题讲解
三、解题必备知识
四、方法总结
五、变式归纳
六、巩固练习
七、巩固练习参考答案
试卷第1页,共3页
试卷第1页,共3页
