【班海精品】冀教版(新)七下-6.1 二元一次方程组 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)七下-6.1 二元一次方程组 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
6.1 二元一次方程组
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判断下列式子是否是一元一次方程:
回顾旧知
一元一次方程
1、只有一个未知数
2、未知数的指数是一次
3、方程的两边都是整式
新课精讲
探索新知
1
知识点
二元一次方程
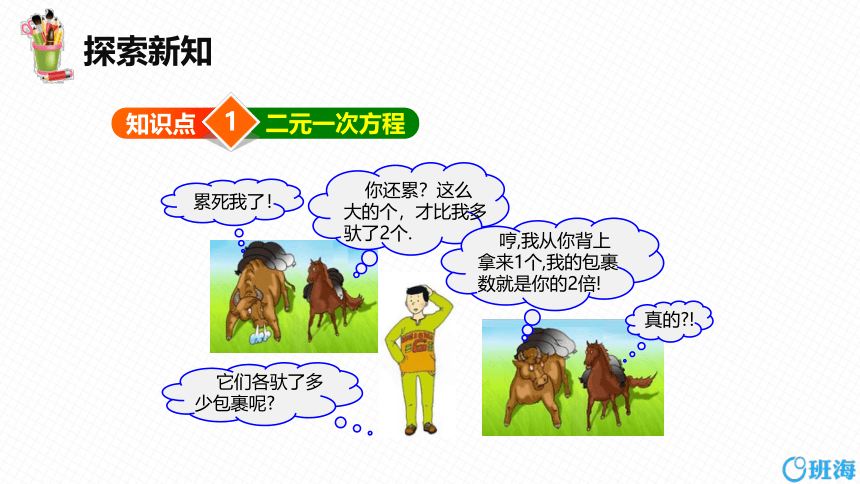
累死我了!
你还累?这么
大的个,才比我多
驮了2个.
哼,我从你背上
拿来1个,我的包裹
数就是你的2倍!
真的 !
它们各驮了多
少包裹呢
探索新知
设老牛驮了 x个包裹,小马驮了 y个包裹 .
老牛驮的包裹数比小马驮的多2个,由此你能得
到怎样的方程?
若老牛从小马背上拿来1个包裹,这时它们各有
几个包裹?由此你又能得到怎样的方程?
探索新知
想一想:
上面两个问题中,我们分别得到方程x-y=2,
和x+1=2(y-1) .这些方程各含有几个未知数?
含未知数的项的次数是多少?
1、只含有两个未知数
2、未知数的最高次数是1次
可以发现
3、方程的两边必须是整式
二元
一次
整式方程
探索新知
含有两个未知数,并且所含未知数的项的
次数都是1的方程叫做二元一次方程.
定义
(1)二元一次方程的条件:
①整式方程;
②只含两个未知数;
③两个未知数系数都不为0;
④含有未知数的项的次数都是1 .
(2)二元一次方程的一般形式:ax+by=c(a≠0,b≠0).
探索新知
例1 有下列方程:①xy =1; ②2x=3y; ③
④x2+y=3; ⑤ ⑥ax2+2x+3y=0
(a=0),其中,二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
导引:根据二元一次方程的定义,①含未知数的项xy的次数是2;③不是整式方程;④含未知数的项x2,y中,x2的次数不是1.只有②⑤⑥满足.其中⑥已指明a=0,所以ax2=0,则方程化简后为2x+3y=0.
C
探索新知
总 结
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都
不为0且含未知数的项的次数都是1.
典题精讲
把方程2x+y=4写成用含x的代数式表示y的形式:
y=__________.
2 下列方程中,哪个是二元一次方程?
(1) xy=3; (2) 2x2-y=9;
(3) (4) 8x-y=3.
-2x+4
解:(4).
典题精讲
在下列式子:① ② ③3x+y2-2=0;
④x=y;⑤x+y-z-1=8; ⑥2xy+9=0中,是二元一次方
程的是_______.(填序号)
① ④
4 下列各式中,是二元一次方程的是( )
A.x-4=y2 B.4x+y=6z
C. +1=y D.5x-2y=19
D
探索新知
2
知识点
二元一次方程的解
二元一次方程的解:
定义:适合一个二元一次方程的一组未知数的值,
叫做这个二元一次方程的一个解.
探索新知
例2 若 是方程4x-3y=10的一个解,求m的值.
导引:由二元一次方程解的定义知,方程的解一定能使方程左右两
边的值相等.因此将 代入方程4x-3y=10中,即可得到一个关于m的一元一次方程.
解:由题意,得4(3m+1)-3(2m-2)=10 . 解这个方程,得m=0 .
探索新知
总 结
已知二元一次方程的解确定字母参数的方法是:将方程的解代入方程中,得到一个关于这个字母参数的新方程,解这个方程即可求出这个字母参数的值.
典题精讲
1 x=-3,y=1为下列哪一个二元一次方程的解?( )
A.x+2y=-1 B.x-2y=1
C.2x+3y=6 D.2x-3y=-6
A
已知 是方程2x-ay=3的一个解,那么a的值是( )
A.1 B.3
C.-3 D.-1
A
探索新知
3
知识点
用含一个未知数的式子表示另一个未知数
二元一次方程x+y=6,
(1)用含有x的代数式表示y为__________;
(2)用含有y的代数式表示x为__________ .
y=6-x
x=6-y
探索新知
例3 在二元一次方程2x-y=3中,请选用一个适当的未知数的代
数式表示另一个未知数 .
解:(1)用含y的代数式表示x:
移项,得:2x=3+y,
∴
(2)用含x的代数式表示y:
移项,得:2x-3=y,
∴y=2x-3 .
探索新知
总 结
用含一个未知数的式子表示另一个未知数的变形步骤为:
(1)移项,把被表示项移到一边,把其他项移到另一边;
(2)化系数为1,在方程两边同除以被表示项的系数.
典题精讲
1 由 可以得到用x表示y的式子为( )
A. B.
C. D.
C
典题精讲
2 如果2x-7y=8,那么用含y的代数式表示x正确的是( )
A. B.
C. D.
C
探索新知
4
知识点
二元一次方程的整数解
例4 求二元一次方程3x+2y=12的非负整数解.
导引:对于二元一次方程3x+2y=12而言,它有无数组
解,但它的非负整数解是有限的,可利用尝试取
值的方法逐个验证.
解: 原方程可化为
因为x,y都是非负整数,
探索新知
所以必须保证12-3x能被2整除,
所以x必为偶数.
而由
所以x=0或2或4 .
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0,
所以原方程的非负整数解为
x≥0,得0≤x≤4,
探索新知
总 结
求二元一次方程的整数解的方法:
(1)变形:把x看成常数,把方程变形为用x表示y的形式;
(2)划界:根据方程的解都是整数的特点,划定x的取值范围;
(3)试值:在x的取值范围内逐一试值;
(4)确定:根据试值结果得到二元一次方程的整数解.其求解流程可概述为:变形
用x表示y
确定x的范围
逐一验证
划界
确定.
试值
典题精讲
1 二元一次方程2x+y=5的正整数解有( )
A.1组 B.2组
C.3组 D.4组
B
2 足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队共进行了6场比赛,得了12分,该队获胜的场数可能是( )
A.1或2 B.2或3
C.3或4 D.4或5
C
学以致用
若(m+2)x |m|-1+y 2n+m=5是关于x,y的二元一次方程,则m
=_____,n=______.
2
小试牛刀
方程ax-4y=x-1是关于x,y的二元一次方程,则a的取值范
围为( )
A.a≠0 B.a≠-1
C.a≠1 D.a≠2
C
小试牛刀
3 若xa+2+yb-1=-3是关于x,y的二元一次方程,则a,b应满足( )
A.a=1,b=1 B.a=-1,b=1
C.a=-1,b=2 D.a=1,b=2
C
4 方程(m2-9)x2+x-(m+3)y=0是关于x,y的二元一次方程,则
m的值为( )
A.±3 B.3 C.-3 D.9
B
小试牛刀
5 下列各组数中,不是二元一次方程2x+y=6的解的是( )
B.
C. D.
C
小试牛刀
6 有一根40 cm的金属棒,欲将其截成x根7 cm的小段和y根9 cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.x=1,y=3 B.x=4,y=1
C.x=3,y=2 D.x=2,y=3
C
小试牛刀
7 已知关于x,y的方程(m2-4)x2+(m+2)x+(m+1)y=m+5.
(1)当m为何值时,它是一元一次方程?
(2)当m为何值时,它是二元一次方程?
由题意得m2-4=0,解得m=2或m=-2.
(1)当m=-2时,m+2=0,m+1≠0,
此时方程为一元一次方程.
(2)当m=2时,原方程可化为4x+3y=7,
此时方程为二元一次方程.
解:
小试牛刀
8.若 是二元一次方程4x-3y=10的一组解,求m的值.
将 代入方程4x-3y=10,
得4(3m+1)-3(2m-2)=10,解得m=0 .
解:
小试牛刀
9.某电视台黄金时段的2 min广告时间内,插播时间分别为15 s和30 s的两种广告,15 s的广告每播1次收费0.6万元,30 s的广告每播1次收费1万元,要求每种广告播放不少于2次.若设15 s的广告播放x次,30 s的广告播放y次.
(1)试写出关于x,y的方程.
(2)两种广告播放的次数有哪几种安排方式?
(3)电视台选择哪种方式播放,收益最大?最大收益是多少?
(2)因为x,y为正整数,且x≥2,y≥2,所以满足15x+30y=120,
即x+2y=8的解只有两组:
所以两种广告播放的次数有两种安排方式:①15 s的广告播放4次,
30 s的广告播放2次;②15 s的广告播放2次,30 s的广告播放3次.
解:
(1)15x+30y=120.
小试牛刀
(3)因为按方式①所得收益为0.6×4+1×2=4.4(万元),
按方式②所得收益为0.6×2+1×3=4.2(万元),所以按15 s的广告播放4次,30 s的广告播放2次所得的收益最大,最大收益是4.4万元.
9.某电视台黄金时段的2 min广告时间内,插播时间分别为15 s和30 s的两种广告,15 s的广告每播1次收费0.6万元,30 s的广告每播1次收费1万元,要求每种广告播放不少于2次.若设15 s的广告播放x次,30 s的广告播放y次.
(3)电视台选择哪种方式播放,收益最大?最大收益是多少?
课堂小结
课堂小结
1.二元一次方程的特征:
(1)是整式方程;
(2)只含有两个未知数;
(3)含有未知数的项的次数都是1;
(4)能整理成ax+by=c的形式,且a≠0,b≠0.
2. 二元一次方程的解:
(1)二元一次方程的解一般都有无数多个;其整数解一般是有限个;
(2)每个解都是一对实数,通常用大括号联立.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6.1 二元一次方程组
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判断下列式子是否是一元一次方程:
回顾旧知
一元一次方程
1、只有一个未知数
2、未知数的指数是一次
3、方程的两边都是整式
新课精讲
探索新知
1
知识点
二元一次方程
累死我了!
你还累?这么
大的个,才比我多
驮了2个.
哼,我从你背上
拿来1个,我的包裹
数就是你的2倍!
真的 !
它们各驮了多
少包裹呢
探索新知
设老牛驮了 x个包裹,小马驮了 y个包裹 .
老牛驮的包裹数比小马驮的多2个,由此你能得
到怎样的方程?
若老牛从小马背上拿来1个包裹,这时它们各有
几个包裹?由此你又能得到怎样的方程?
探索新知
想一想:
上面两个问题中,我们分别得到方程x-y=2,
和x+1=2(y-1) .这些方程各含有几个未知数?
含未知数的项的次数是多少?
1、只含有两个未知数
2、未知数的最高次数是1次
可以发现
3、方程的两边必须是整式
二元
一次
整式方程
探索新知
含有两个未知数,并且所含未知数的项的
次数都是1的方程叫做二元一次方程.
定义
(1)二元一次方程的条件:
①整式方程;
②只含两个未知数;
③两个未知数系数都不为0;
④含有未知数的项的次数都是1 .
(2)二元一次方程的一般形式:ax+by=c(a≠0,b≠0).
探索新知
例1 有下列方程:①xy =1; ②2x=3y; ③
④x2+y=3; ⑤ ⑥ax2+2x+3y=0
(a=0),其中,二元一次方程有( )
A.1个 B.2个 C.3个 D.4个
导引:根据二元一次方程的定义,①含未知数的项xy的次数是2;③不是整式方程;④含未知数的项x2,y中,x2的次数不是1.只有②⑤⑥满足.其中⑥已指明a=0,所以ax2=0,则方程化简后为2x+3y=0.
C
探索新知
总 结
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都
不为0且含未知数的项的次数都是1.
典题精讲
把方程2x+y=4写成用含x的代数式表示y的形式:
y=__________.
2 下列方程中,哪个是二元一次方程?
(1) xy=3; (2) 2x2-y=9;
(3) (4) 8x-y=3.
-2x+4
解:(4).
典题精讲
在下列式子:① ② ③3x+y2-2=0;
④x=y;⑤x+y-z-1=8; ⑥2xy+9=0中,是二元一次方
程的是_______.(填序号)
① ④
4 下列各式中,是二元一次方程的是( )
A.x-4=y2 B.4x+y=6z
C. +1=y D.5x-2y=19
D
探索新知
2
知识点
二元一次方程的解
二元一次方程的解:
定义:适合一个二元一次方程的一组未知数的值,
叫做这个二元一次方程的一个解.
探索新知
例2 若 是方程4x-3y=10的一个解,求m的值.
导引:由二元一次方程解的定义知,方程的解一定能使方程左右两
边的值相等.因此将 代入方程4x-3y=10中,即可得到一个关于m的一元一次方程.
解:由题意,得4(3m+1)-3(2m-2)=10 . 解这个方程,得m=0 .
探索新知
总 结
已知二元一次方程的解确定字母参数的方法是:将方程的解代入方程中,得到一个关于这个字母参数的新方程,解这个方程即可求出这个字母参数的值.
典题精讲
1 x=-3,y=1为下列哪一个二元一次方程的解?( )
A.x+2y=-1 B.x-2y=1
C.2x+3y=6 D.2x-3y=-6
A
已知 是方程2x-ay=3的一个解,那么a的值是( )
A.1 B.3
C.-3 D.-1
A
探索新知
3
知识点
用含一个未知数的式子表示另一个未知数
二元一次方程x+y=6,
(1)用含有x的代数式表示y为__________;
(2)用含有y的代数式表示x为__________ .
y=6-x
x=6-y
探索新知
例3 在二元一次方程2x-y=3中,请选用一个适当的未知数的代
数式表示另一个未知数 .
解:(1)用含y的代数式表示x:
移项,得:2x=3+y,
∴
(2)用含x的代数式表示y:
移项,得:2x-3=y,
∴y=2x-3 .
探索新知
总 结
用含一个未知数的式子表示另一个未知数的变形步骤为:
(1)移项,把被表示项移到一边,把其他项移到另一边;
(2)化系数为1,在方程两边同除以被表示项的系数.
典题精讲
1 由 可以得到用x表示y的式子为( )
A. B.
C. D.
C
典题精讲
2 如果2x-7y=8,那么用含y的代数式表示x正确的是( )
A. B.
C. D.
C
探索新知
4
知识点
二元一次方程的整数解
例4 求二元一次方程3x+2y=12的非负整数解.
导引:对于二元一次方程3x+2y=12而言,它有无数组
解,但它的非负整数解是有限的,可利用尝试取
值的方法逐个验证.
解: 原方程可化为
因为x,y都是非负整数,
探索新知
所以必须保证12-3x能被2整除,
所以x必为偶数.
而由
所以x=0或2或4 .
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0,
所以原方程的非负整数解为
x≥0,得0≤x≤4,
探索新知
总 结
求二元一次方程的整数解的方法:
(1)变形:把x看成常数,把方程变形为用x表示y的形式;
(2)划界:根据方程的解都是整数的特点,划定x的取值范围;
(3)试值:在x的取值范围内逐一试值;
(4)确定:根据试值结果得到二元一次方程的整数解.其求解流程可概述为:变形
用x表示y
确定x的范围
逐一验证
划界
确定.
试值
典题精讲
1 二元一次方程2x+y=5的正整数解有( )
A.1组 B.2组
C.3组 D.4组
B
2 足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队共进行了6场比赛,得了12分,该队获胜的场数可能是( )
A.1或2 B.2或3
C.3或4 D.4或5
C
学以致用
若(m+2)x |m|-1+y 2n+m=5是关于x,y的二元一次方程,则m
=_____,n=______.
2
小试牛刀
方程ax-4y=x-1是关于x,y的二元一次方程,则a的取值范
围为( )
A.a≠0 B.a≠-1
C.a≠1 D.a≠2
C
小试牛刀
3 若xa+2+yb-1=-3是关于x,y的二元一次方程,则a,b应满足( )
A.a=1,b=1 B.a=-1,b=1
C.a=-1,b=2 D.a=1,b=2
C
4 方程(m2-9)x2+x-(m+3)y=0是关于x,y的二元一次方程,则
m的值为( )
A.±3 B.3 C.-3 D.9
B
小试牛刀
5 下列各组数中,不是二元一次方程2x+y=6的解的是( )
B.
C. D.
C
小试牛刀
6 有一根40 cm的金属棒,欲将其截成x根7 cm的小段和y根9 cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )
A.x=1,y=3 B.x=4,y=1
C.x=3,y=2 D.x=2,y=3
C
小试牛刀
7 已知关于x,y的方程(m2-4)x2+(m+2)x+(m+1)y=m+5.
(1)当m为何值时,它是一元一次方程?
(2)当m为何值时,它是二元一次方程?
由题意得m2-4=0,解得m=2或m=-2.
(1)当m=-2时,m+2=0,m+1≠0,
此时方程为一元一次方程.
(2)当m=2时,原方程可化为4x+3y=7,
此时方程为二元一次方程.
解:
小试牛刀
8.若 是二元一次方程4x-3y=10的一组解,求m的值.
将 代入方程4x-3y=10,
得4(3m+1)-3(2m-2)=10,解得m=0 .
解:
小试牛刀
9.某电视台黄金时段的2 min广告时间内,插播时间分别为15 s和30 s的两种广告,15 s的广告每播1次收费0.6万元,30 s的广告每播1次收费1万元,要求每种广告播放不少于2次.若设15 s的广告播放x次,30 s的广告播放y次.
(1)试写出关于x,y的方程.
(2)两种广告播放的次数有哪几种安排方式?
(3)电视台选择哪种方式播放,收益最大?最大收益是多少?
(2)因为x,y为正整数,且x≥2,y≥2,所以满足15x+30y=120,
即x+2y=8的解只有两组:
所以两种广告播放的次数有两种安排方式:①15 s的广告播放4次,
30 s的广告播放2次;②15 s的广告播放2次,30 s的广告播放3次.
解:
(1)15x+30y=120.
小试牛刀
(3)因为按方式①所得收益为0.6×4+1×2=4.4(万元),
按方式②所得收益为0.6×2+1×3=4.2(万元),所以按15 s的广告播放4次,30 s的广告播放2次所得的收益最大,最大收益是4.4万元.
9.某电视台黄金时段的2 min广告时间内,插播时间分别为15 s和30 s的两种广告,15 s的广告每播1次收费0.6万元,30 s的广告每播1次收费1万元,要求每种广告播放不少于2次.若设15 s的广告播放x次,30 s的广告播放y次.
(3)电视台选择哪种方式播放,收益最大?最大收益是多少?
课堂小结
课堂小结
1.二元一次方程的特征:
(1)是整式方程;
(2)只含有两个未知数;
(3)含有未知数的项的次数都是1;
(4)能整理成ax+by=c的形式,且a≠0,b≠0.
2. 二元一次方程的解:
(1)二元一次方程的解一般都有无数多个;其整数解一般是有限个;
(2)每个解都是一对实数,通常用大括号联立.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
