【班海精品】冀教版(新)七下-6.2 二元一次方程组的解法 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)七下-6.2 二元一次方程组的解法 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 17:25:54 | ||
图片预览










文档简介
(共37张PPT)
6.1 二元一次方程组
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
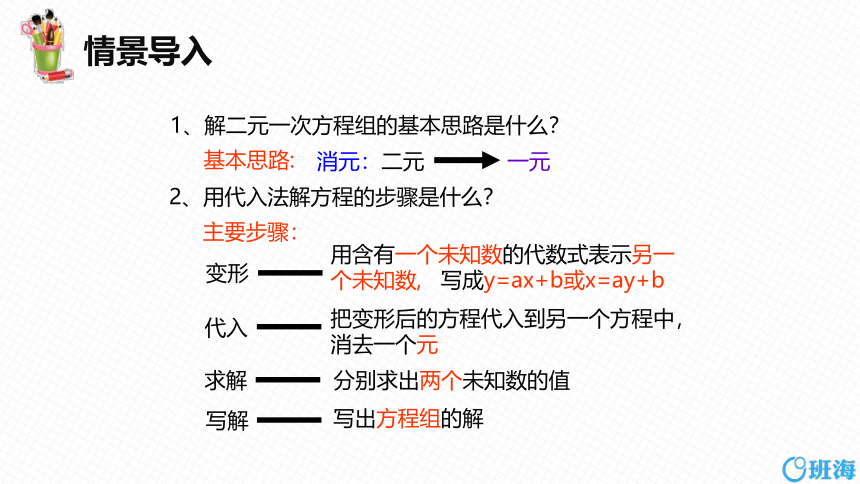
情景导入
主要步骤:
基本思路:
写解
求解
代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b或x=ay+b
消元:二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
新课精讲
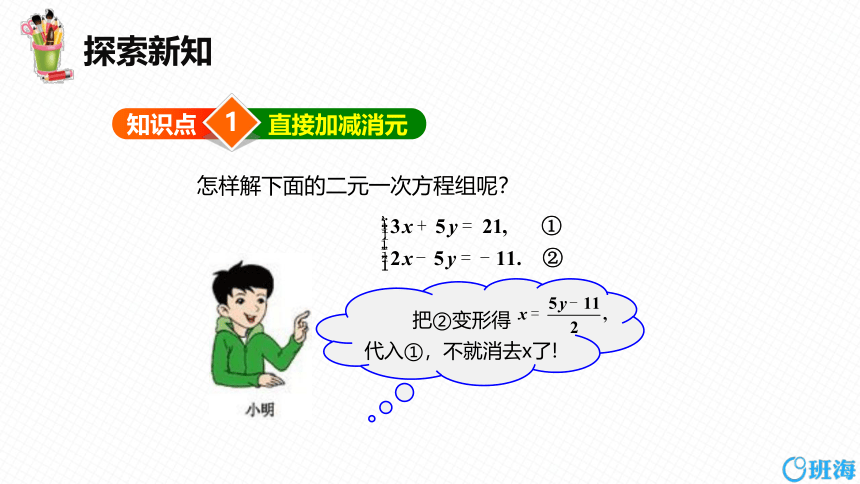
探索新知
1
知识点
直接加减消元
把②变形得 代入①,不就消去x了!
怎样解下面的二元一次方程组呢?
探索新知
按小丽的思路,你能消去一个未知数吗
把②变形得5y=2x+11,可以直接代入①呀!
5y和-5y互为相反数……
探索新知
两个方程相加,可以得到5x = 10,
x = 2 .
将x = 2代入①,得 6 + 5y = 21,
y = 3 .
所以方程组
的解是
探索新知
加减法定义:
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
探索新知
解:①+②,得7x=14,
x=2 .
将x=2代入①,得10+3y=16,
y=2 .
所以,原方程组的解是
例1 解方程组:
探索新知
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,然后解答方程即可.
总 结
典题精讲
1 用加减消元法解下列方程组:
①+②,得2x=8,x=4.
把x=4代入①,得4+y=5,y=1.
所以原方程组的解为
解:
①+②,得16x=-16,x=-1 .
把x=-1代入①,得7×(-1)-2y=3,
解得y=-5.
所以原方程组的解为
解:
典题精讲
2 用加减法解方程组 时,①-②得( )
A.5y=2 B.-11y=8
C.-11y=2 D.5y=8
A
3 解方程组 时,用加减消元法最简便的是( )
A.①+② B.①-②
C.①×2-②×3 D.①×3+②×2
A
探索新知
2
知识点
先变形,再加减消元
如果二元一次方程组的未知数的系数相同或互为相反数,我们可以运用加减法来解.那么对于一些系数不同或不互为相反数的二元一次方程组,还能用加减法来解吗?
探索新知
(1)两个方程同一未知数的系数的绝对值如果相等或成倍数关系,解方程组时考虑用加减消元法.
(2)如果同一未知数的系数的绝对值既不相等又不成倍数关系,我们应设法将一个未知数的系数的绝对值转化为相等关系.
(3)用加减法时,一般选择系数比较简单(同一未知数的系数的绝对值相等或成倍数关系)的未知数作为消元对象.
探索新知
例2 解方程组:
解:
②×2,得4x+6y=8, ③
①-③,得x=-1 .
把x=-1代入②,得 -2+3y=4,
y=2 .
所以,原方程组的解为
探索新知
例3 解方程组:
导引:方程组中,两个方程中y的系数的绝对值成倍数关系,方程②乘以3就可与方程①相加消去y .
解: 由②×3,得 51x-9y=222,③
由①+③,得 59x=295,解得 x=5 .
把x=5代入①,得8×5+9y=73,解得
所以原方程组的解为
典题精讲
1 用加减消元法解下列方程组:
②-①×2,得5n=5,n=1.
把n=1代入①,
得m-1=1,m=2 .
所以原方程组的解为
解:
①×2,得2x+4y+4=0 . ③
③+②,得9x+45=0,x=-5 .
把x=-5代入①,
得-5+2y+2=0,解得 y=
所以原方程组的解为
解:
典题精讲
2 利用加减消元法解方程组 下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
D
典题精讲
3 用加减法解方程组 时,要使两个方程中同一未知数的系数相等或互为相反数,有以下四种变形的结果:
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
B
探索新知
3
知识点
解方程组的应用
例4 解方程组:
导引:方程①和②中x,y的系数的绝对值都不相等,也不成倍数关系,应取系数的绝对值的最小公倍数6,可以先消去x,也可以先消去y .
探索新知
解:方法一:①×3,得6x+9y=9 . ③
②×2,得6x+4y=22 . ④
③-④,得5y=-13,即
把
解得
所以这个方程组的解为
代入①,得
方法二:①×2,得4x+6y=6 . ⑤
②×3,得9x+6y=33 . ⑥
⑥-⑤,得5x=27,解得
把
解得
所以这个方程组的解为
代入①,得
探索新知
总 结
用加减消元法解二元一次方程组时,一般有三种情况:
①方程组中某个未知数的系数的绝对值相等,则直接利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,但某个未知数的系数的绝对值成倍数关系,则其中一个方程乘这个倍数后再利用加减法求解;
③方程组中任一个未知数的系数的绝对值既不相等,也不成倍数关系,可利用最小公倍数的知识,把两个方程都适当地乘一个数,使某个未知数的系数的绝对值相等,然后再利用加减法求解.
典题精讲
若方程组 的解也是二元一次方程5x-my=-11的一
个解,则m的值等于( )
A.5 B.-7
C.-5 D.7
D
典题精讲
2 小明在某商店购买商品A,B共两次,这两次购买商品A,B的数量和费用如表:若小丽需要购买3个商品A和2个商品B,则她要花费( )
A.64元 B.65元 C.66元 D.67元
C
购买商品A的数量/个 购买商品B的数量/个 购买总
费用/元
第一次购物 4 3 93
第二次购物 6 6 162
学以致用
小试牛刀
方程组 中,x的系数的特点是______,方程组
中,y的系数的特点是____________, 这两个方程组用_______消
元法解较简便.
相等
互为相反数
加减
方程组 既可以用_________消去未知数_____;也
可以用_________________消去未知数______.
①+②
y
①-②或②-①
x
小试牛刀
3 已知x,y满足方程组 则x+y的值为( )
A.9 B.7
C.5 D.3
A
小试牛刀
4 解方程组:
解:
小试牛刀
5.选择适当的方法解方程组.
(1)
解:
(2)
小试牛刀
6.已知关于x,y的二元一次方程组 的解互为相反数,求k的值.
解:
小试牛刀
7. 小明想从“天猫”某网店购买计算器,经查询,某品牌A型号计算器的单价比B型号计算器的单价多10元,5台A型号的计算器与7台B型号的计算器的价钱相同,问A,B两种型号计算器的单价分别是多少?
解:
小试牛刀
8. 请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算?并说明理由.
小试牛刀
解:
(2)
(1)
课堂小结
课堂小结
用加减消元法解二元一次方程组的一般步骤:
(1)变形:将方程组中某一未知数的系数变为相等或相反.
(2)加减:消去一个未知数.
(3)求解:得到一个未知数的值.
(4)回代:求另一个未知数的值.
(5)写出解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6.1 二元一次方程组
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
主要步骤:
基本思路:
写解
求解
代入
把变形后的方程代入到另一个方程中,消去一个元
分别求出两个未知数的值
写出方程组的解
变形
用含有一个未知数的代数式表示另一个未知数, 写成y=ax+b或x=ay+b
消元:二元
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
一元
新课精讲
探索新知
1
知识点
直接加减消元
把②变形得 代入①,不就消去x了!
怎样解下面的二元一次方程组呢?
探索新知
按小丽的思路,你能消去一个未知数吗
把②变形得5y=2x+11,可以直接代入①呀!
5y和-5y互为相反数……
探索新知
两个方程相加,可以得到5x = 10,
x = 2 .
将x = 2代入①,得 6 + 5y = 21,
y = 3 .
所以方程组
的解是
探索新知
加减法定义:
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法,简称加减法.
探索新知
解:①+②,得7x=14,
x=2 .
将x=2代入①,得10+3y=16,
y=2 .
所以,原方程组的解是
例1 解方程组:
探索新知
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程,然后解答方程即可.
总 结
典题精讲
1 用加减消元法解下列方程组:
①+②,得2x=8,x=4.
把x=4代入①,得4+y=5,y=1.
所以原方程组的解为
解:
①+②,得16x=-16,x=-1 .
把x=-1代入①,得7×(-1)-2y=3,
解得y=-5.
所以原方程组的解为
解:
典题精讲
2 用加减法解方程组 时,①-②得( )
A.5y=2 B.-11y=8
C.-11y=2 D.5y=8
A
3 解方程组 时,用加减消元法最简便的是( )
A.①+② B.①-②
C.①×2-②×3 D.①×3+②×2
A
探索新知
2
知识点
先变形,再加减消元
如果二元一次方程组的未知数的系数相同或互为相反数,我们可以运用加减法来解.那么对于一些系数不同或不互为相反数的二元一次方程组,还能用加减法来解吗?
探索新知
(1)两个方程同一未知数的系数的绝对值如果相等或成倍数关系,解方程组时考虑用加减消元法.
(2)如果同一未知数的系数的绝对值既不相等又不成倍数关系,我们应设法将一个未知数的系数的绝对值转化为相等关系.
(3)用加减法时,一般选择系数比较简单(同一未知数的系数的绝对值相等或成倍数关系)的未知数作为消元对象.
探索新知
例2 解方程组:
解:
②×2,得4x+6y=8, ③
①-③,得x=-1 .
把x=-1代入②,得 -2+3y=4,
y=2 .
所以,原方程组的解为
探索新知
例3 解方程组:
导引:方程组中,两个方程中y的系数的绝对值成倍数关系,方程②乘以3就可与方程①相加消去y .
解: 由②×3,得 51x-9y=222,③
由①+③,得 59x=295,解得 x=5 .
把x=5代入①,得8×5+9y=73,解得
所以原方程组的解为
典题精讲
1 用加减消元法解下列方程组:
②-①×2,得5n=5,n=1.
把n=1代入①,
得m-1=1,m=2 .
所以原方程组的解为
解:
①×2,得2x+4y+4=0 . ③
③+②,得9x+45=0,x=-5 .
把x=-5代入①,
得-5+2y+2=0,解得 y=
所以原方程组的解为
解:
典题精讲
2 利用加减消元法解方程组 下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(-5)+②×2
D
典题精讲
3 用加减法解方程组 时,要使两个方程中同一未知数的系数相等或互为相反数,有以下四种变形的结果:
其中变形正确的是( )
A.①② B.③④ C.①③ D.②④
B
探索新知
3
知识点
解方程组的应用
例4 解方程组:
导引:方程①和②中x,y的系数的绝对值都不相等,也不成倍数关系,应取系数的绝对值的最小公倍数6,可以先消去x,也可以先消去y .
探索新知
解:方法一:①×3,得6x+9y=9 . ③
②×2,得6x+4y=22 . ④
③-④,得5y=-13,即
把
解得
所以这个方程组的解为
代入①,得
方法二:①×2,得4x+6y=6 . ⑤
②×3,得9x+6y=33 . ⑥
⑥-⑤,得5x=27,解得
把
解得
所以这个方程组的解为
代入①,得
探索新知
总 结
用加减消元法解二元一次方程组时,一般有三种情况:
①方程组中某个未知数的系数的绝对值相等,则直接利用加减法求解;
②方程组中任一个未知数的系数的绝对值都不相等,但某个未知数的系数的绝对值成倍数关系,则其中一个方程乘这个倍数后再利用加减法求解;
③方程组中任一个未知数的系数的绝对值既不相等,也不成倍数关系,可利用最小公倍数的知识,把两个方程都适当地乘一个数,使某个未知数的系数的绝对值相等,然后再利用加减法求解.
典题精讲
若方程组 的解也是二元一次方程5x-my=-11的一
个解,则m的值等于( )
A.5 B.-7
C.-5 D.7
D
典题精讲
2 小明在某商店购买商品A,B共两次,这两次购买商品A,B的数量和费用如表:若小丽需要购买3个商品A和2个商品B,则她要花费( )
A.64元 B.65元 C.66元 D.67元
C
购买商品A的数量/个 购买商品B的数量/个 购买总
费用/元
第一次购物 4 3 93
第二次购物 6 6 162
学以致用
小试牛刀
方程组 中,x的系数的特点是______,方程组
中,y的系数的特点是____________, 这两个方程组用_______消
元法解较简便.
相等
互为相反数
加减
方程组 既可以用_________消去未知数_____;也
可以用_________________消去未知数______.
①+②
y
①-②或②-①
x
小试牛刀
3 已知x,y满足方程组 则x+y的值为( )
A.9 B.7
C.5 D.3
A
小试牛刀
4 解方程组:
解:
小试牛刀
5.选择适当的方法解方程组.
(1)
解:
(2)
小试牛刀
6.已知关于x,y的二元一次方程组 的解互为相反数,求k的值.
解:
小试牛刀
7. 小明想从“天猫”某网店购买计算器,经查询,某品牌A型号计算器的单价比B型号计算器的单价多10元,5台A型号的计算器与7台B型号的计算器的价钱相同,问A,B两种型号计算器的单价分别是多少?
解:
小试牛刀
8. 请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算?并说明理由.
小试牛刀
解:
(2)
(1)
课堂小结
课堂小结
用加减消元法解二元一次方程组的一般步骤:
(1)变形:将方程组中某一未知数的系数变为相等或相反.
(2)加减:消去一个未知数.
(3)求解:得到一个未知数的值.
(4)回代:求另一个未知数的值.
(5)写出解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
