【班海精品】冀教版(新)七下-6.2 二元一次方程组的解法 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)七下-6.2 二元一次方程组的解法 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-11 17:25:54 | ||
图片预览










文档简介
(共31张PPT)
6.1 二元一次方程组
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、用含x的代数式表示y:
x + y = 22
2、用含y的代数式表示x:
2x - 7y = 8
回顾旧知:
新课精讲
探索新知
1
知识点
代入消元法
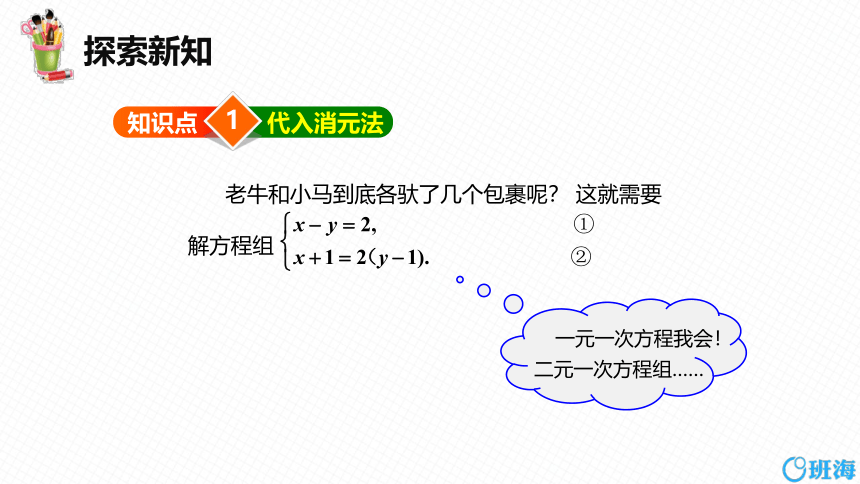
老牛和小马到底各驮了几个包裹呢? 这就需要
解方程组
一元一次方程我会!
二元一次方程组……
探索新知
由①,得 y=x-2. ③
由于方程组中相同的字母代表同一对象,所以方程②
中的y也等于x- 2, 可以用x- 2代替方程②中的y . 这样有
x+1=2(x-2-1). ④
解所得的一元一次方程④,得x = 7.
再把x = 7代入③,得 y=5 .
啊哈,二元
化为一元了!
探索新知
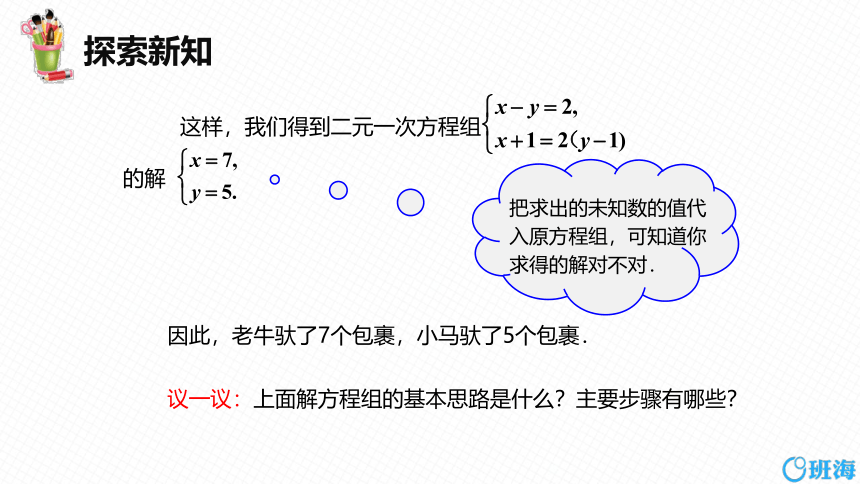
这样,我们得到二元一次方程组
的解
因此,老牛驮了7个包裹,小马驮了5个包裹.
把求出的未知数的值代入原方程组,可知道你求得的解对不对.
议一议:上面解方程组的基本思路是什么?主要步骤有哪些?
探索新知
1.消元思想:
二元一次方程组中有两个未知数,如果消去其中一个未知数,那么就把二元一次方程组转化为一元一次方程,先求出一个未知数,然后再求另一个未知数,这种将未知数的个数由多化少,逐一解决的思想,叫消元思想.
2.代入消元:
(1)定义:将二元一次方程组中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程组的方法称为代入消元法,简称代入法.
探索新知
(2)用代入消元法解二元一次方程组的一般步骤及方法:
①变形为y=ax+b(或x=ay+b)的形式;
②代入;
③求出一个未知数;
④求出另一个未知数;
⑤写出解 .
探索新知
例1 求二元一次方程组 的解 .
将①代入②,得x+2(x-6)=9.
解这个一元一次方程,得x=7.
将x=7代入① ,得y=1.
所以原方程组的解是
解:
探索新知
例2 解方程组:
解:由②,得 x=13-4y, ③
将③代入①,得 2(13-4y)+3y=16,
26-8y+3y=16,
-5y=-10,
y=2 .
将y=2代入③,得 x=5 . 以原方程组的解是
典题精讲
1 用代入消元法解下列方程组:
把①代入②,得3x+2(2x-3)=8.
解得x=2 . 把x=2代入①,得y=1.
所以原方程组的解为
解:
由①,得y=4x-27. ③
把③代入②,得2x+3(4x-27)=3.
解得x=6 . 把x=6代入③,得y=-3.
所以原方程组的解为
典题精讲
2 用代入法解方程组 下列说法正确的是( )
A.直接把①代入②,消去y
B.直接把①代入②,消去x
C.直接把②代入①,消去y
D.直接把②代入①,消去x
B
典题精讲
3 用代入法解方程组 比较合理的变形是( )
A.由①得 B.由①得
C.由②得 D.由②得y=2x-5
D
4 方程组 的解是( )
A. B. C. D.
D
探索新知
2
知识点
代入消元法的应用
(4). 写解
(3). 解
(2). 代
分别求出两个未知数的值
写出方程组的解
(1). 变
用一个未知数的代数式
表示另一个未知数
2、用代入法解方程的主要步骤:
消去一个元
探索新知
例3 解方程组:
导引:
方程①中y的系数为1,用含x的式子表示y,然后用代入法解方程组.
解:
由①,得y=4-x . ③
把③代入②,得2x-3(4-x)=3,
解这个方程,得x=3 .
把x=3代入③,得y=1 .
所以这个方程组的解是
探索新知
总 结
利用代入法解方程组的思路:将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元方程为一元方程.用代入法解方程组时,选择方程用一个未知数表示另一个未知数是解题关键,它影响着解题繁简程度,因此应尽量选取系数比较简单的方程 .
典题精讲
1 若(a+b+5)2+|2a-b+1|=0,则(b-a)2 019等于( )
A.-1 B.1
C.52 019 D.-52 019
A
2 若单项式2x2ya+b与- xa-by4是同类项,则a,b的值分别是( )
A.a=3,b=1 B.a=-3,b=1
C.a=3,b=-1 D.a=-3,b=-1
A
典题精讲
3 关于x,y的方程组 则y用只含x的式子表示为( )
A.y=2x+7 B.y=7-2x
C.y=-2x-5 D.y=2x-5
B
学以致用
小试牛刀
1 下列用代入法解方程组 的步骤,其中最简单的是( )
A.由①,得 ,③ 把③代入②,得3× =11-2y
B.由①,得y=3x-2,③ 把③代入②,得3x=11-2(3x-2)
C.由②,得 ,③ 把③代入①,得3x- =2
D.把②代入①,得11-2y-y=2(把3x看成一个整体)
D
小试牛刀
2 用代入法解方程组 较简单的方法是( )
A.消y B.消x
C.消x和消y一样 D.无法确定
A
3 “六一”前夕,市关工委准备为希望小学购进图书和文具若干套,已知1套文具和3套图书需104元,3套文具和2套图书需116元,则1套文具和1套图书需______元.
48
小试牛刀
4.用代入法解下列方程组.
(1)
解:
(2)
小试牛刀
5.已知关于x,y的二元一次方程组 的解满足x+y=0,求m的值.
解关于x,y的方程组
因为x+y=0,所以(2m-11)+(-m+7)=0,
解得m=4 .
解:
小试牛刀
6 解方程组:
将②变形得x=8+3y,③
把③代入①,得2(8+3y)+3y=7,解得y=-1 .
把y=-1代入③,得x=5 .
所以这个方程组的解是
解:
小试牛刀
7.如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是多少克?
解:
小试牛刀
8.小明在解方程组 时,得到的解是 小英同样解这个方程组,由于把c抄错而得到的解是 求方程组中a,b,c的值.
依题意,可知
解得c=-5.由题意,可知
是方程ax+by=2的解,即2a-6b=2 .
解方程组
综上可知,a= ,b= ,c=-5 .
解:
课堂小结
课堂小结
利用代入消元法解二元一次方程组的关键是找准代入式,在方程组中选择一个系数最简单(尤其是未知数前的系数为±1)的方程,进行变形后代入另一个方程,从而消元求出方程组的解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6.1 二元一次方程组
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、用含x的代数式表示y:
x + y = 22
2、用含y的代数式表示x:
2x - 7y = 8
回顾旧知:
新课精讲
探索新知
1
知识点
代入消元法
老牛和小马到底各驮了几个包裹呢? 这就需要
解方程组
一元一次方程我会!
二元一次方程组……
探索新知
由①,得 y=x-2. ③
由于方程组中相同的字母代表同一对象,所以方程②
中的y也等于x- 2, 可以用x- 2代替方程②中的y . 这样有
x+1=2(x-2-1). ④
解所得的一元一次方程④,得x = 7.
再把x = 7代入③,得 y=5 .
啊哈,二元
化为一元了!
探索新知
这样,我们得到二元一次方程组
的解
因此,老牛驮了7个包裹,小马驮了5个包裹.
把求出的未知数的值代入原方程组,可知道你求得的解对不对.
议一议:上面解方程组的基本思路是什么?主要步骤有哪些?
探索新知
1.消元思想:
二元一次方程组中有两个未知数,如果消去其中一个未知数,那么就把二元一次方程组转化为一元一次方程,先求出一个未知数,然后再求另一个未知数,这种将未知数的个数由多化少,逐一解决的思想,叫消元思想.
2.代入消元:
(1)定义:将二元一次方程组中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程组的方法称为代入消元法,简称代入法.
探索新知
(2)用代入消元法解二元一次方程组的一般步骤及方法:
①变形为y=ax+b(或x=ay+b)的形式;
②代入;
③求出一个未知数;
④求出另一个未知数;
⑤写出解 .
探索新知
例1 求二元一次方程组 的解 .
将①代入②,得x+2(x-6)=9.
解这个一元一次方程,得x=7.
将x=7代入① ,得y=1.
所以原方程组的解是
解:
探索新知
例2 解方程组:
解:由②,得 x=13-4y, ③
将③代入①,得 2(13-4y)+3y=16,
26-8y+3y=16,
-5y=-10,
y=2 .
将y=2代入③,得 x=5 . 以原方程组的解是
典题精讲
1 用代入消元法解下列方程组:
把①代入②,得3x+2(2x-3)=8.
解得x=2 . 把x=2代入①,得y=1.
所以原方程组的解为
解:
由①,得y=4x-27. ③
把③代入②,得2x+3(4x-27)=3.
解得x=6 . 把x=6代入③,得y=-3.
所以原方程组的解为
典题精讲
2 用代入法解方程组 下列说法正确的是( )
A.直接把①代入②,消去y
B.直接把①代入②,消去x
C.直接把②代入①,消去y
D.直接把②代入①,消去x
B
典题精讲
3 用代入法解方程组 比较合理的变形是( )
A.由①得 B.由①得
C.由②得 D.由②得y=2x-5
D
4 方程组 的解是( )
A. B. C. D.
D
探索新知
2
知识点
代入消元法的应用
(4). 写解
(3). 解
(2). 代
分别求出两个未知数的值
写出方程组的解
(1). 变
用一个未知数的代数式
表示另一个未知数
2、用代入法解方程的主要步骤:
消去一个元
探索新知
例3 解方程组:
导引:
方程①中y的系数为1,用含x的式子表示y,然后用代入法解方程组.
解:
由①,得y=4-x . ③
把③代入②,得2x-3(4-x)=3,
解这个方程,得x=3 .
把x=3代入③,得y=1 .
所以这个方程组的解是
探索新知
总 结
利用代入法解方程组的思路:将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程中,从而消去一个未知数,化二元方程为一元方程.用代入法解方程组时,选择方程用一个未知数表示另一个未知数是解题关键,它影响着解题繁简程度,因此应尽量选取系数比较简单的方程 .
典题精讲
1 若(a+b+5)2+|2a-b+1|=0,则(b-a)2 019等于( )
A.-1 B.1
C.52 019 D.-52 019
A
2 若单项式2x2ya+b与- xa-by4是同类项,则a,b的值分别是( )
A.a=3,b=1 B.a=-3,b=1
C.a=3,b=-1 D.a=-3,b=-1
A
典题精讲
3 关于x,y的方程组 则y用只含x的式子表示为( )
A.y=2x+7 B.y=7-2x
C.y=-2x-5 D.y=2x-5
B
学以致用
小试牛刀
1 下列用代入法解方程组 的步骤,其中最简单的是( )
A.由①,得 ,③ 把③代入②,得3× =11-2y
B.由①,得y=3x-2,③ 把③代入②,得3x=11-2(3x-2)
C.由②,得 ,③ 把③代入①,得3x- =2
D.把②代入①,得11-2y-y=2(把3x看成一个整体)
D
小试牛刀
2 用代入法解方程组 较简单的方法是( )
A.消y B.消x
C.消x和消y一样 D.无法确定
A
3 “六一”前夕,市关工委准备为希望小学购进图书和文具若干套,已知1套文具和3套图书需104元,3套文具和2套图书需116元,则1套文具和1套图书需______元.
48
小试牛刀
4.用代入法解下列方程组.
(1)
解:
(2)
小试牛刀
5.已知关于x,y的二元一次方程组 的解满足x+y=0,求m的值.
解关于x,y的方程组
因为x+y=0,所以(2m-11)+(-m+7)=0,
解得m=4 .
解:
小试牛刀
6 解方程组:
将②变形得x=8+3y,③
把③代入①,得2(8+3y)+3y=7,解得y=-1 .
把y=-1代入③,得x=5 .
所以这个方程组的解是
解:
小试牛刀
7.如图所示的两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是多少克?
解:
小试牛刀
8.小明在解方程组 时,得到的解是 小英同样解这个方程组,由于把c抄错而得到的解是 求方程组中a,b,c的值.
依题意,可知
解得c=-5.由题意,可知
是方程ax+by=2的解,即2a-6b=2 .
解方程组
综上可知,a= ,b= ,c=-5 .
解:
课堂小结
课堂小结
利用代入消元法解二元一次方程组的关键是找准代入式,在方程组中选择一个系数最简单(尤其是未知数前的系数为±1)的方程,进行变形后代入另一个方程,从而消元求出方程组的解.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
