【班海精品】冀教版(新)七下-7.2 相交线 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)七下-7.2 相交线 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:35 | ||
图片预览











文档简介
(共55张PPT)
7.2 相 交 线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示是北京天安门
广场庄严隆重的升国旗仪式,
是亿万中国人民特别关注的
活动.众所周知,1949年10
月1日,毛泽东主席在天安
门城楼上用洪亮的声音向全
世界宣告中华人民共和国诞
生,亲手升起了第一面五星
红旗.
情景导入
天安门广场的升国旗仪式一招一式欣赏性极强,人们概括有“五绝”.一绝:升旗;二绝:护旗;三绝:敬礼;四绝:礼毕;五绝:收旗.其中的每招每式都有极其严格的要求.每一次,当擎旗手以优美的动作,在国歌奏响第一个音符时,将国旗展开抛出,到国歌的最后一个音符终止,都是2分07秒,国旗也准时到达30米高的旗杆顶端,做到了分秒不差.可是,你看着旗杆
与地面,会想到旗杆与地面有怎样的位置关系呢?
新课精讲
探索新知
1
知识点
垂 直
观察思考
当转动一木条的位置时,什么也随着发生了变化?
探索新知
a
b
在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直.
垂足
垂 线
垂
线
探索新知
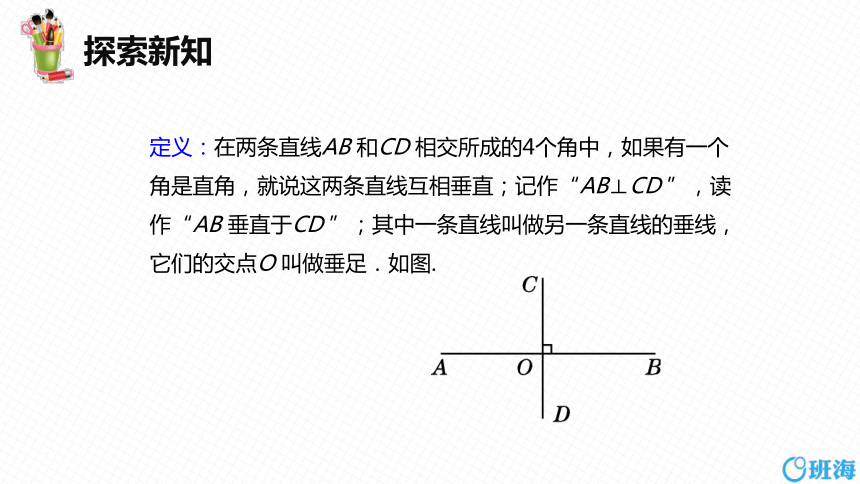
定义:在两条直线AB 和CD 相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直;记作“AB⊥CD ”,读作“AB 垂直于CD ”;其中一条直线叫做另一条直线的垂线,它们的交点O 叫做垂足.如图.
探索新知
导引:要判断OE,OF 是什么位置关系,其实质是说明OE,OF 是否垂直,即要看∠EOF 是否为90°;要让∠EOF=90°,需说明∠EOF=∠AOC 或∠EOF=∠BOC 都可,这样就把问题转化为说明∠AOE=∠COF (已知)了.
例1 如图,CO⊥AB于点O,∠AOE=∠COF,则射
线OE,OF 是什么位置关系?请说明理由.
探索新知
解:射线OE,OF 互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE 与OF 互相垂直(垂直定义).
探索新知
总 结
判断两直线(线段、射线所在直线)互相垂直,主要
依据是垂直定义,只要说明两条相交直线所构成的四
个角中有一个角是直角即可.
典题精讲
如图,已知点O 在直线AB上,CO⊥DO 于点O,若∠1=145°,则∠3的度数为( )
A.35°
B.45°
C.55°
D.65°
1
C
典题精讲
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2等于( )
A.30°
B.34°
C.45°
D.56°
2
B
典题精讲
如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD 的度数是( )
A.117°
B.127°
C.153°
D.163°
3
C
探索新知
2
知识点
垂线的确定性
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线. 并记上直角符号“﹁”.
探索新知
归 纳
经过直线上或直线外一点,有且只有一条直
线与已知直线垂直.
探索新知
已知直线AB,CB,l 在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是下图中的( )
例2
A B C D
C
探索新知
根据题意可知,过点B 有AB,CB 都与直线l 垂
直,由垂线的基本事实可知,在同一平面内,
过一点有且只有一条直线与已知直线垂直,所
以A,B,C 三点在一条直线上.
导引:
探索新知
总 结
利用直线的性质解答题目,要注意直线性质满足的条件:
1.在平面内;
2.过一点,点的位置可以在直线上也可以在直线外;
3.相交所成的角必须是直角,以上三条缺一不可.
典题精讲
1
如图,已知直线AB,CD 和点E,过点E 分别画出直线AB,CD 的垂线.
如图,EF⊥CD,
EG⊥AB.
解:
典题精讲
2
下列选项中,过点P 画AB 的垂线,三角尺放法正确的是( )
C
典题精讲
过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上
B.这条线段的端点处
C.这条线段的延长线上
D.以上都有可能
3
D
探索新知
3
知识点
垂线段的最短性
思考
如图,在灌溉时,要把河中的水引到农田P 处,
如何挖渠能使渠道最短?
探索新知
连接直线外一点与直线上各点的所有线段中,垂线段最短.
P
A
B
C
m
D
简单说成:垂线段最短.
探索新知
归 纳
连接直线外一点与直线上各点的所有线段中,
垂线段最短.
简单说成:垂线段最短.
探索新知
如图所示,AB 是一条河流,要铺设管道将河水引
到C、D 两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D 作AB 的垂线,垂足分别为点E,F,沿CE,DF 铺设管道;
方案二:连接CD 交AB 于点P,
沿PC,PD 铺设管道.
这两种铺设管道的方案哪一种
更节省材料?为什么?
(忽略河流的宽度)
例3
探索新知
要尽可能节省材料,也就是让管道的总长度最短.方案一中CE,DF 是垂线段,而方案二中PC,PD 不是垂线段,所以CE<PC,DF<PD,所以CE+DF<PC+PD,所以方案一更节省材料.
解:
导引:
按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,CD 不垂直于AB,
根据“垂线段最短”可知,CE<PC,DF<DP,
所以CE+DF<PC+DP.
所以沿CE,DF 铺设管道更节省材料.
探索新知
总 结
本题主要利用“垂线段最短”来解决实际问题,
解这类求最短距离问题时,要注意“垂线段最短”与
“两点之间,线段最短”的区别,辨明这两条性质的应用条件:点到直线的距离,两点间的距离;正确运用解题方法.
典题精讲
1
如图,要把河中的水引到水池C,在河岸AB 的什么地方开始挖渠,才能使水渠的长度最短?
如图,作CD⊥AB,垂足为点D. 由垂线段最短,可知在河岸AB 的点D 处开始挖渠,才能使水渠的长度最短.
解:
典题精讲
如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点
B.B点
C.C点
D.D点
2
A
探索新知
4
知识点
点到直线的距离
从直线外一点到这条直线所画垂直线段的长度叫做这点到直线的距离.
探索新知
例4 如图,在三角形ABC 中,∠ACB=90°,CD⊥
AB,垂足为D.若AC=4 cm,BC=3 cm,AB=
5 cm,则点A 到直线BC 的距离为______cm,点
B 到直线AC 的距离为______cm,点C 到直线AB
的距离为______cm.
4
3
2.4
探索新知
导引:根据点到直线的距离的定义可知,点A 到直线BC
的距离是线段AC 的长,点B 到直线AC 的距离是线段BC 的长,点C 到直线AB 的距离是线段CD 的长.因为三角形ABC 的面积S= 所以AC·BC=AB ·CD,进而可得CD=2.4 cm.
探索新知
总 结
正确理解点到直线的距离及两点间的距离是解决
此类问题的关键.解决此类问题应注意:(1)点到直线
的距离是点到直线的垂线段的长度,而不是垂线,也
不是垂线段;(2)距离表示线段的长度,是一个数量,
与线段不能等同;(3)用垂线段的长度表示点到直线的
距离,其实质是点与垂足两点间的距离,体现了数形
结合思想.
典题精讲
1
如图,在测量跳远成绩的示意图中,直线l是起跳线,BP,AP,AO 中哪一条线段的长度是跳远的成绩?
O
P
线段AO 的长度是跳远的成绩.
解:
典题精讲
下列说法中,正确的有( )
①过两点有且只有一条直线;
②连接两点的线段叫做两点的距离;
③两点之间,垂线最短;
④若AB=BC,则点B 是线段AC 的中点.
A.1个 B.2个
C.3个 D.4个
2
A
易错提醒
已知△ABC 中,BC=6,AC=3,CP⊥AB,垂足为P,则CP 的长可能是( )
A.2 B.4
C.5 D.7
易错点:对垂线段的性质理解不透彻而致错
A
学以致用
小试牛刀
已知在同一平面内:
①两条直线相交成直角;
②两条直线互相垂直;
③一条直线是另一条直线的垂线.
那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A.0个 B.1个 C.2个 D.3个
D
1
小试牛刀
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM 与ON 重合(即O,M,N 三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且
只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线
与已知直线垂直
D.两点之间,线段最短
C
2
小试牛刀
3 如图,AD⊥BD,BC⊥CD,AB=6 cm,BC=4 cm,
则BD 的长度的取值范围是( )
A.大于4 cm
B.小于6 cm
C.大于4 cm或小于 6 cm
D.大于 4 cm且小于 6 cm
D
小试牛刀
如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )
A.2条
B.3条
C.4条
D.5条
D
4
小试牛刀
5
已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD 的度数.
(2)如图②,若∠BOC=60°,求∠AOD 的度数.
(3)根据(1)(2)结果猜想∠AOD 与∠BOC 有怎样的关系?并
根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=
7∶29,求∠BOC 和∠AOD 的度数.
小试牛刀
(1)因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB - ∠ BOC = 90°-50°=40°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)因为OA⊥OB,所以∠AOB=90°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=360°-∠AOB-∠BOC-∠COD=360°-90°-60°-90°=120°.
解:
小试牛刀
(3)∠AOD 与∠BOC 互补.理由:因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB-∠BOC=90°-∠BOC.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=90°-∠BOC+90°=180°-∠BOC,所以∠AOD+∠BOC=180°,即∠AOD 与∠BOC 互补.
(4)已知∠BOC+∠AOD=180°,又因为∠BOC : ∠AOD=7:29,所以∠BOC=35°,∠AOD=145°.
小试牛刀
6
如图,直线AB,CD 相交于点O,P 是CD上一点.
(1)过点P 画AB 的垂线段PE;
(2)过点P 画CD 的垂线,与AB 相交于F 点;
(3)说明线段PE,PO,FO 三者的大小关系,其依据是什么?
小试牛刀
(1)如图.
(2)如图.
(3)PE<PO<FO,其依据是垂线段最短.
解:
小试牛刀
平原上有A,B,C,D 四个村庄,为解决当地缺水问题,
政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H的位置,使它到四个村庄的距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明依据.
7
小试牛刀
(1)如图,连接AD,BC,交于点H,则H 点为蓄水池的位置,它到四个村庄距离之和最小.
(2)如图,过点H 作HG⊥EF,垂足为G,则沿HG开渠最短.依据:直线外一点与直线上各点连接的所有线段中,垂线段最短.
解:
小试牛刀
8
在如图所示的直角三角形ABC 中,斜边为BC,两直角边分
别为AB,AC,设BC=a,AC=b,AB=c.
(1)试用所学知识说明斜边BC 是最长的边;
(2)试化简|a-b|+|c-a|+|b+c-a|.
小试牛刀
(1)因为点C 与直线AB上点A,B 的连线中,CA是垂线段,所以AC<BC.因为点B与直线AC上点A,C 的连线中,AB 是垂线段,所以AB<BC.故AB,AC,BC 中,斜边BC 最长.
(2)因为BC>AC,AB<BC,AC+AB>BC,所以原式=a-b-(c-a)+b+c-a=a.
解:
课堂小结
课堂小结
以下几个方面由学生自己总结:
1.垂线的定义及垂直的符号表示;
2.垂线的有关性质;
3.过一点作已知直线的垂线的方法;
4.点到直线的距离.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
7.2 相 交 线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示是北京天安门
广场庄严隆重的升国旗仪式,
是亿万中国人民特别关注的
活动.众所周知,1949年10
月1日,毛泽东主席在天安
门城楼上用洪亮的声音向全
世界宣告中华人民共和国诞
生,亲手升起了第一面五星
红旗.
情景导入
天安门广场的升国旗仪式一招一式欣赏性极强,人们概括有“五绝”.一绝:升旗;二绝:护旗;三绝:敬礼;四绝:礼毕;五绝:收旗.其中的每招每式都有极其严格的要求.每一次,当擎旗手以优美的动作,在国歌奏响第一个音符时,将国旗展开抛出,到国歌的最后一个音符终止,都是2分07秒,国旗也准时到达30米高的旗杆顶端,做到了分秒不差.可是,你看着旗杆
与地面,会想到旗杆与地面有怎样的位置关系呢?
新课精讲
探索新知
1
知识点
垂 直
观察思考
当转动一木条的位置时,什么也随着发生了变化?
探索新知
a
b
在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直.
垂足
垂 线
垂
线
探索新知
定义:在两条直线AB 和CD 相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直;记作“AB⊥CD ”,读作“AB 垂直于CD ”;其中一条直线叫做另一条直线的垂线,它们的交点O 叫做垂足.如图.
探索新知
导引:要判断OE,OF 是什么位置关系,其实质是说明OE,OF 是否垂直,即要看∠EOF 是否为90°;要让∠EOF=90°,需说明∠EOF=∠AOC 或∠EOF=∠BOC 都可,这样就把问题转化为说明∠AOE=∠COF (已知)了.
例1 如图,CO⊥AB于点O,∠AOE=∠COF,则射
线OE,OF 是什么位置关系?请说明理由.
探索新知
解:射线OE,OF 互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE 与OF 互相垂直(垂直定义).
探索新知
总 结
判断两直线(线段、射线所在直线)互相垂直,主要
依据是垂直定义,只要说明两条相交直线所构成的四
个角中有一个角是直角即可.
典题精讲
如图,已知点O 在直线AB上,CO⊥DO 于点O,若∠1=145°,则∠3的度数为( )
A.35°
B.45°
C.55°
D.65°
1
C
典题精讲
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2等于( )
A.30°
B.34°
C.45°
D.56°
2
B
典题精讲
如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD 的度数是( )
A.117°
B.127°
C.153°
D.163°
3
C
探索新知
2
知识点
垂线的确定性
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线. 并记上直角符号“﹁”.
探索新知
归 纳
经过直线上或直线外一点,有且只有一条直
线与已知直线垂直.
探索新知
已知直线AB,CB,l 在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是下图中的( )
例2
A B C D
C
探索新知
根据题意可知,过点B 有AB,CB 都与直线l 垂
直,由垂线的基本事实可知,在同一平面内,
过一点有且只有一条直线与已知直线垂直,所
以A,B,C 三点在一条直线上.
导引:
探索新知
总 结
利用直线的性质解答题目,要注意直线性质满足的条件:
1.在平面内;
2.过一点,点的位置可以在直线上也可以在直线外;
3.相交所成的角必须是直角,以上三条缺一不可.
典题精讲
1
如图,已知直线AB,CD 和点E,过点E 分别画出直线AB,CD 的垂线.
如图,EF⊥CD,
EG⊥AB.
解:
典题精讲
2
下列选项中,过点P 画AB 的垂线,三角尺放法正确的是( )
C
典题精讲
过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上
B.这条线段的端点处
C.这条线段的延长线上
D.以上都有可能
3
D
探索新知
3
知识点
垂线段的最短性
思考
如图,在灌溉时,要把河中的水引到农田P 处,
如何挖渠能使渠道最短?
探索新知
连接直线外一点与直线上各点的所有线段中,垂线段最短.
P
A
B
C
m
D
简单说成:垂线段最短.
探索新知
归 纳
连接直线外一点与直线上各点的所有线段中,
垂线段最短.
简单说成:垂线段最短.
探索新知
如图所示,AB 是一条河流,要铺设管道将河水引
到C、D 两个用水点,现有两种铺设管道的方案:
方案一:分别过点C,D 作AB 的垂线,垂足分别为点E,F,沿CE,DF 铺设管道;
方案二:连接CD 交AB 于点P,
沿PC,PD 铺设管道.
这两种铺设管道的方案哪一种
更节省材料?为什么?
(忽略河流的宽度)
例3
探索新知
要尽可能节省材料,也就是让管道的总长度最短.方案一中CE,DF 是垂线段,而方案二中PC,PD 不是垂线段,所以CE<PC,DF<PD,所以CE+DF<PC+PD,所以方案一更节省材料.
解:
导引:
按方案一铺设管道更节省材料,理由如下:
因为CE⊥AB,DF⊥AB,CD 不垂直于AB,
根据“垂线段最短”可知,CE<PC,DF<DP,
所以CE+DF<PC+DP.
所以沿CE,DF 铺设管道更节省材料.
探索新知
总 结
本题主要利用“垂线段最短”来解决实际问题,
解这类求最短距离问题时,要注意“垂线段最短”与
“两点之间,线段最短”的区别,辨明这两条性质的应用条件:点到直线的距离,两点间的距离;正确运用解题方法.
典题精讲
1
如图,要把河中的水引到水池C,在河岸AB 的什么地方开始挖渠,才能使水渠的长度最短?
如图,作CD⊥AB,垂足为点D. 由垂线段最短,可知在河岸AB 的点D 处开始挖渠,才能使水渠的长度最短.
解:
典题精讲
如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点
B.B点
C.C点
D.D点
2
A
探索新知
4
知识点
点到直线的距离
从直线外一点到这条直线所画垂直线段的长度叫做这点到直线的距离.
探索新知
例4 如图,在三角形ABC 中,∠ACB=90°,CD⊥
AB,垂足为D.若AC=4 cm,BC=3 cm,AB=
5 cm,则点A 到直线BC 的距离为______cm,点
B 到直线AC 的距离为______cm,点C 到直线AB
的距离为______cm.
4
3
2.4
探索新知
导引:根据点到直线的距离的定义可知,点A 到直线BC
的距离是线段AC 的长,点B 到直线AC 的距离是线段BC 的长,点C 到直线AB 的距离是线段CD 的长.因为三角形ABC 的面积S= 所以AC·BC=AB ·CD,进而可得CD=2.4 cm.
探索新知
总 结
正确理解点到直线的距离及两点间的距离是解决
此类问题的关键.解决此类问题应注意:(1)点到直线
的距离是点到直线的垂线段的长度,而不是垂线,也
不是垂线段;(2)距离表示线段的长度,是一个数量,
与线段不能等同;(3)用垂线段的长度表示点到直线的
距离,其实质是点与垂足两点间的距离,体现了数形
结合思想.
典题精讲
1
如图,在测量跳远成绩的示意图中,直线l是起跳线,BP,AP,AO 中哪一条线段的长度是跳远的成绩?
O
P
线段AO 的长度是跳远的成绩.
解:
典题精讲
下列说法中,正确的有( )
①过两点有且只有一条直线;
②连接两点的线段叫做两点的距离;
③两点之间,垂线最短;
④若AB=BC,则点B 是线段AC 的中点.
A.1个 B.2个
C.3个 D.4个
2
A
易错提醒
已知△ABC 中,BC=6,AC=3,CP⊥AB,垂足为P,则CP 的长可能是( )
A.2 B.4
C.5 D.7
易错点:对垂线段的性质理解不透彻而致错
A
学以致用
小试牛刀
已知在同一平面内:
①两条直线相交成直角;
②两条直线互相垂直;
③一条直线是另一条直线的垂线.
那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A.0个 B.1个 C.2个 D.3个
D
1
小试牛刀
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM 与ON 重合(即O,M,N 三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且
只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线
与已知直线垂直
D.两点之间,线段最短
C
2
小试牛刀
3 如图,AD⊥BD,BC⊥CD,AB=6 cm,BC=4 cm,
则BD 的长度的取值范围是( )
A.大于4 cm
B.小于6 cm
C.大于4 cm或小于 6 cm
D.大于 4 cm且小于 6 cm
D
小试牛刀
如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )
A.2条
B.3条
C.4条
D.5条
D
4
小试牛刀
5
已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD 的度数.
(2)如图②,若∠BOC=60°,求∠AOD 的度数.
(3)根据(1)(2)结果猜想∠AOD 与∠BOC 有怎样的关系?并
根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=
7∶29,求∠BOC 和∠AOD 的度数.
小试牛刀
(1)因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB - ∠ BOC = 90°-50°=40°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)因为OA⊥OB,所以∠AOB=90°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=360°-∠AOB-∠BOC-∠COD=360°-90°-60°-90°=120°.
解:
小试牛刀
(3)∠AOD 与∠BOC 互补.理由:因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB-∠BOC=90°-∠BOC.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=90°-∠BOC+90°=180°-∠BOC,所以∠AOD+∠BOC=180°,即∠AOD 与∠BOC 互补.
(4)已知∠BOC+∠AOD=180°,又因为∠BOC : ∠AOD=7:29,所以∠BOC=35°,∠AOD=145°.
小试牛刀
6
如图,直线AB,CD 相交于点O,P 是CD上一点.
(1)过点P 画AB 的垂线段PE;
(2)过点P 画CD 的垂线,与AB 相交于F 点;
(3)说明线段PE,PO,FO 三者的大小关系,其依据是什么?
小试牛刀
(1)如图.
(2)如图.
(3)PE<PO<FO,其依据是垂线段最短.
解:
小试牛刀
平原上有A,B,C,D 四个村庄,为解决当地缺水问题,
政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H的位置,使它到四个村庄的距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明依据.
7
小试牛刀
(1)如图,连接AD,BC,交于点H,则H 点为蓄水池的位置,它到四个村庄距离之和最小.
(2)如图,过点H 作HG⊥EF,垂足为G,则沿HG开渠最短.依据:直线外一点与直线上各点连接的所有线段中,垂线段最短.
解:
小试牛刀
8
在如图所示的直角三角形ABC 中,斜边为BC,两直角边分
别为AB,AC,设BC=a,AC=b,AB=c.
(1)试用所学知识说明斜边BC 是最长的边;
(2)试化简|a-b|+|c-a|+|b+c-a|.
小试牛刀
(1)因为点C 与直线AB上点A,B 的连线中,CA是垂线段,所以AC<BC.因为点B与直线AC上点A,C 的连线中,AB 是垂线段,所以AB<BC.故AB,AC,BC 中,斜边BC 最长.
(2)因为BC>AC,AB<BC,AC+AB>BC,所以原式=a-b-(c-a)+b+c-a=a.
解:
课堂小结
课堂小结
以下几个方面由学生自己总结:
1.垂线的定义及垂直的符号表示;
2.垂线的有关性质;
3.过一点作已知直线的垂线的方法;
4.点到直线的距离.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
