【班海精品】冀教版(新)七下-8.4 整式的乘法 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)七下-8.4 整式的乘法 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:35 | ||
图片预览










文档简介
(共45张PPT)
8.4 整式的乘法
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
旧知回顾
单项式与单项式相乘,只要把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里出现的字母,则连同它的指数一起作为积的一个因式。
情景导入
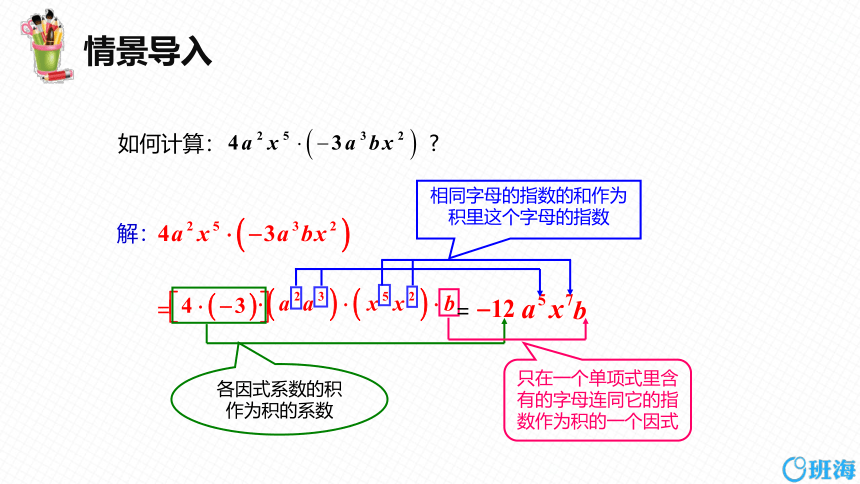
如何计算:
解:
=
=
相同字母的指数的和作为积里这个字母的指数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
各因式系数的积作为积的系数
情景导入
怎样计算m (a+b)呢?
m 是一个单项式,a+b 是一个多项式,这是一个单
项式与多项式相乘的问题.
由于字母a,b 都代表数,所以可以用分配律进行
计算,即
m (a+b)=ma+mb.
新课精讲
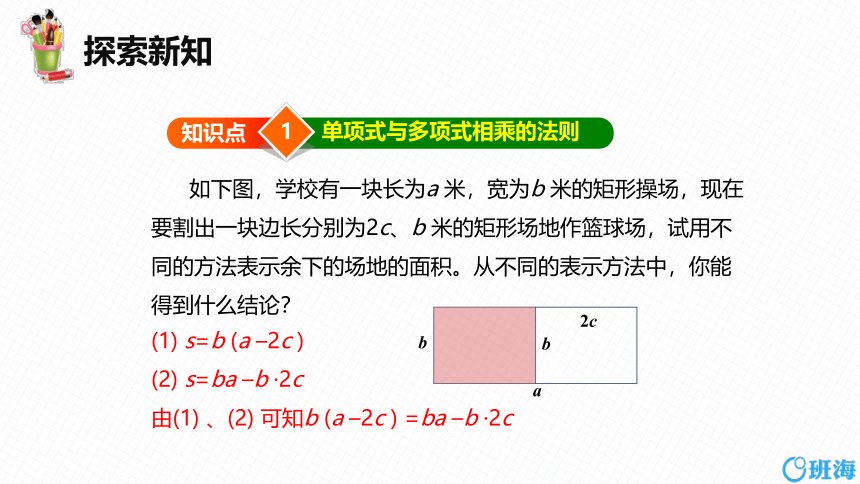
(1) s=b (a –2c )
(2) s=ba –b ·2c
由(1) 、(2) 可知b (a –2c ) =ba –b ·2c
探索新知
1
知识点
单项式与多项式相乘的法则
如下图,学校有一块长为a 米,宽为b 米的矩形操场,现在要割出一块边长分别为2c、b 米的矩形场地作篮球场,试用不同的方法表示余下的场地的面积。从不同的表示方法中,你能得到什么结论?
b
a
2c
b
探索新知
单项式与多项式相乘,用单项式去乘多项式的每
一项,再把积相加.
归 纳
探索新知
(1)单项式与多项式相乘,实质上是利用乘法分配律将
其转化为单项式乘以单项式的问题.
(2)单项式与多项式相乘,结果是一个多项式,其项数
与因式中多项式的项数相同.
(3)计算过程要注意符号,单项式乘多项式的每一项时,
要包括它前面的符号,同时还要注意单项式的符号.
(4)对于混合运算,应注意运算顺序;最后有同类项时,
必须合并同类项从而得到最简结果.
探索新知
例1
计算:
(1) ab (a 2+b 2) ;(2) -x (2x-3) .
(1) ab (a2+b2)
=ab ·a 2+ab ·b 2
=a 3b+ab 3.
(2) -x (2x-3)
=(-x )×(2x )+ (-x )×(-3)
=-2x 2+3x.
解:
探索新知
总 结
单项式与多项式相乘时,依据法则将其转化为
单项式与单项式相乘,相乘每两项的积用“+”号
相连,然后按单项式与单项式相乘的法则逐个计算,
特别要注意符号.
典题精讲
1
计算:
(1) 8b 2(2a 2-ab-b 2); (2) ab 2 (3a -6b).
(1)8b 2(2a 2-ab-b 2)=8b 2·2a 2-8b 2·ab-8b 2·b 2
=16a 2b 2-8ab 3-8b 4.
(2) ab 2(3a-6b)= ab 2·3a- ab 2·6b
=2a 2b 2-4ab 3.
解:
典题精讲
计算:
(1)3x (4x 2y-2xy 2);
(2)3a (2a 2-a+2);
(3)(-2ab)2·(3a+2b-1);
(4) ·(-4x ).
2
典题精讲
(1)3x (4x 2y-2xy 2)=3x ·4x 2y-3x ·2xy 2=12x 3y-6x 2y 2.
(2)3a (2a 2-a+2)=3a ·2a 2-3a ·a+3a ·2=6a 3-3a 2+6a.
(3)(-2ab)2·(3a+2b-1)=4a 2b 2·(3a+2b-1)=4a 2b 2·3a+4a 2b 2·2b-4a 2b 2=12a 3b 2+8a 2b 3-4a 2b 2.
(4) ·(-4x)
= xy ·(-4x )- y ·(-4x )-y 2·(-4x )
=-3x 2y+2xy+4xy 2
解:
典题精讲
计算:
(1)a (a-b)+3b (a+4b);
(2)3a (a 2+3a-2)-3(a 3+2a 2-a+1) ;
(3)2x (-xy )2-x 2(x 2y 2-y 2).
3
典题精讲
(1)a (a-b)+3b (a+4b)=a 2-ab+3ab+12b 2=a 2+2ab+12b 2.
(2)3a (a 2+3a-2)-3(a 3+2a 2-a+1)=3a 3+9a 2-6a-3a 3-6a 2+3a-3=3a 2-3a-3.
(3)2x (-xy)2-x 2(x 2y 2-y 2)=2x ·x 2y 2-x 2(x 2y 2-y 2)=2x 3y 2-x 4y 2+x 2y 2.
解:
典题精讲
4
计算: 2ab (a 2b+ab-ab 2)-ab 2(a 2-2ab+2a)
2ab (a 2b+ab-ab 2)-ab 2(a 2-2ab+2a)=2ab ·a 2b+2ab ·ab-2ab ·ab 2-ab 2·a 2+
ab 2·2ab-ab 2·2a=2a 3b 2+2a 2b 2-2a 2b 3-a 3b 2+2a 2b 3-2a 2b 2=a 3b 2.
解:
典题精讲
计算6x ·(3-2x )的结果,与下列哪一个式子相同?( )
A.-12x 2+18x B.-12x 2+3
C.16x D.6x
下列运算正确的是( )
A.-2(a+b)=-2a+2b B.(a 2)3=a 5
C.a 3+4a= a 3 D.3a 2·2a 3=6a 5
5
A
D
6
典题精讲
下列运算错误的是( )
A.-m 2·m 3=-m 5
B.-x 2+2x 2=x 2
C.(-a 3b)2=a 6b 2
D.-2x (x-y )=-2x 2-2xy
如果一个长方形的周长为10,其中长为a,那么该长方形的面积为( )
A.10a B.5a-a 2
C.5a D.10a-a 2
7
D
8
B
探索新知
2
知识点
单项式与多项式相乘法则的应用
例3
先化简,再求值: a 2(a+1)-a (a 2-1).
其中,a=5.
a 2(a+1)-a (a 2-1)
=a 3+a 2-a 3+a
=a 2+a
当a=5时,原式=52+5=30
解:
探索新知
总 结
化简求值得题目,先化简再求值,化简的过程
包括整式的乘法与加减法运算,求值的过程就是直
接代入求值.
典题精讲
先化简,再求值: 2x (x-3y-1)+y (6x-y+2).
其中,x =-3,y =2.
1
2x (x-3y-1)+y (6x-y+2)=2x ·x-2x ·3y-2x+6xy-y ·y+2y=2x 2-2x-y 2+2y.
当x=-3,y=2时,原式=2×(-3)2-2×(-3)-22+2×2=18+6-4+4=24.
解:
典题精讲
先化简,再求值:
ab (ab-2a+2)-2b (a 2b-2ab+2a).其中,a=-1,b=-2.
2
ab (ab-2a+2)-2b (a 2b-2ab+2a)=ab ·ab-ab ·2a+ab ·2-2b ·a 2b+2b ·2ab-2b ·2a=a 2b 2-2a 2b+2ab-
2a 2b 2+4ab 2-4ab=-a 2b 2-2a 2b+4ab 2-2ab.
当a=-1,b=-2时,原式=-(-1)2×(-2)2-2×(-1)2
×(-2)+4×(-1)×(-2)2-2×(-1) ×(-2)=-4+4-16-4=-20.
解:
典题精讲
解方程: x (x-3)+2x (x+2)=3x 2-5.
3
去括号,得x 2-3x+2x 2+4x=3x 2-5.
移项,得x 2-3x+2x 2+4x-3x 2=-5.
合并同类项,得x=-5.
解:
典题精讲
计算下列物体的体积和表面积:
4
典题精讲
圆柱:体积V=πr 2·(3r+3)=3πr 3+3πr 2;
表面积S=2πr 2+2πr (3r+3)=2πr 2+6πr 2+6πr=8πr 2+6πr.
长方体:体积V=(4a-1)·a ·2a=8a 3-2a 2;
表面积S=2[2a ·(4a-1)+2a ·a+a ·(4a-1)]=2(8a 2-2a+2a 2+4a 2-a)=2(14a 2-3a)=
28a 2-6a.
解:
典题精讲
今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy (4y-2x-1)=-12xy 2+6x 2y+□,□的地方被钢笔水弄污了,你认为□内应填写( )
A.3xy B.-3xy
C.-1 D.1
5
A
典题精讲
要使x (x+a)+3x-2b=x 2+5x+4成立,则a,b 的值分别为( )
A.a=-2,b=-2 B.a=2,b=2
C.a=2,b=-2 D.a=-2,b=2
若计算(x 2+ax+5)·(-2x )-6x 2的结果中不含有x 2项,则a 的值为( )
A.-3 B.-
C.0 D.3
6
C
A
7
典题精讲
如图,通过计算大长方形的面积可得到的恒等式为________________________.
8
2a (a+b)=2a 2+2ab
典题精讲
化简:
(1)(-2ab)(3a 2-2ab-4b 2);
(2)3x (2x-3y )-(2x-5y ) ·4x;
(3)5a (a-b+c)-2b (a+b-c)-4c (-a-b-c ).
9
(1)原式=-6a 3b+4a 2b 2+8ab 3.
(2)原式=6x 2-9xy-8x 2+20xy=-2x 2+11xy.
(3)原式=5a 2-5ab+5ac-2ab-2b 2+2bc+4ac+4bc+4c 2=5a 2-2b 2+4c 2-7ab+9ac+6bc.
解:
典题精讲
先化简,再求值:3a (2a 2-4a+3)-2a 2(3a+4),
其中a=-2.
10
原式=6a 3-12a 2+9a-6a 3-8a 2=-20a 2+9a,
当a=-2时,原式=-20×4-9×2=-98.
解:
典题精讲
解方程:2x (x-1)=12+x (2x-5).
11
去括号,得2x 2-2x=12+2x 2-5x,
移项、合并同类项,得3x=12,
系数化为1,得x=4.
解:
易错提醒
下列运算中,正确的是( )
A.-2x (3x 2y-2xy )=-6x 3y-4x 2y
B.2xy 2(-x 2+2y 2+1)=-4x 3y 4
C.(3ab 2-2ab)·abc=3a 2b 3-2a 2b 2
D.(ab)2(2ab 2-c)=2a 3b 4-a 2b 2c
D
易错点:对单项式与多项式相乘的法则理解不透而出错
学以致用
小试牛刀
下列计算错误的是( )
A.-3x (2-x)=-6x+3x 2
B.(2m 2n-3mn 2)(-mn)=-2m 3n 2+3m 2n 3
C.xy (x 2y-xy 2-1)=x 3y 2-x 2y 3
D.
C
1
小试牛刀
2
计算:
小试牛刀
(1)原式=
(2)原式
解:
小试牛刀
3
先化简,再求值:
3(2x+1)+2(3-x ),其中x=-1.
原式=6x+3+6-2x
=4x+9.
当x=-1时,4x+9=4×(-1)+9=5.
解:
已知ab 2=-1,求(-ab)(a 2b 5-ab 3-b)的值.
原式=-a 3b 6+a 2b 4+ab 2=-(ab 2)3+(ab 2)2+ab 2.
当ab 2=-1时,原式=-(-1)3+(-1)2+(-1)=1.
解:
4
小试牛刀
某同学在计算一个多项式乘-3x 2时,算成了加上-3x 2,得到的答案是x 2- x+1,那么正确的计算结果是多少?
设这个多项式为A,则A+(-3x 2)=x 2- x+1,所以A=4x 2- x+1.
所以A ·(-3x 2)= ×(-3x 2)
=-12x 4+ x 3-3x 2.
解:
5
小试牛刀
6
当m,n 为何值时, x [x (x+m)+nx (x+1)+m] 的展开式中不含x 2项和x 3项?
x [x (x+m)+nx (x+1)+m]= x (x 2+mx+nx 2+nx+m)= (1+n)x 3+ (m+n)x 2+ mx,
因为它不含x 2项和x 3项,所以1+n=0,m+n=0,
解得n=-1,m=1.
解:
小试牛刀
7
一张长方形硬纸片,长为(5a 2+4b 2)m,宽为6a 4 m,在它的四个角上分别剪去一个边长为 a3 m的小正方形,然后折成一个无盖的盒子,请你求这个无盖盒子的表面积.
解:
纸片的面积是:(5a 2+4b 2)·6a 4=30a 6+24a 4b 2(m2),
小正方形的面积是: = a 6(m2),
则无盖盒子的表面积是:
30a 6+24a 4b 2-4× a 6=21a 6+24a 4b 2(m2).
课堂小结
课堂小结
1. 单项式与多项式相乘的依据是:乘法对加法的分配律.
2. 单项式与多项式相乘,其积仍是多项式,项数与原
多项式的项数 相同,注意不要漏乘项.
3. 积的每一项的符号由原多项式各项符号和单项式的
符号来决定,注意去括号法则.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
8.4 整式的乘法
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
旧知回顾
单项式与单项式相乘,只要把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里出现的字母,则连同它的指数一起作为积的一个因式。
情景导入
如何计算:
解:
=
=
相同字母的指数的和作为积里这个字母的指数
只在一个单项式里含有的字母连同它的指数作为积的一个因式
各因式系数的积作为积的系数
情景导入
怎样计算m (a+b)呢?
m 是一个单项式,a+b 是一个多项式,这是一个单
项式与多项式相乘的问题.
由于字母a,b 都代表数,所以可以用分配律进行
计算,即
m (a+b)=ma+mb.
新课精讲
(1) s=b (a –2c )
(2) s=ba –b ·2c
由(1) 、(2) 可知b (a –2c ) =ba –b ·2c
探索新知
1
知识点
单项式与多项式相乘的法则
如下图,学校有一块长为a 米,宽为b 米的矩形操场,现在要割出一块边长分别为2c、b 米的矩形场地作篮球场,试用不同的方法表示余下的场地的面积。从不同的表示方法中,你能得到什么结论?
b
a
2c
b
探索新知
单项式与多项式相乘,用单项式去乘多项式的每
一项,再把积相加.
归 纳
探索新知
(1)单项式与多项式相乘,实质上是利用乘法分配律将
其转化为单项式乘以单项式的问题.
(2)单项式与多项式相乘,结果是一个多项式,其项数
与因式中多项式的项数相同.
(3)计算过程要注意符号,单项式乘多项式的每一项时,
要包括它前面的符号,同时还要注意单项式的符号.
(4)对于混合运算,应注意运算顺序;最后有同类项时,
必须合并同类项从而得到最简结果.
探索新知
例1
计算:
(1) ab (a 2+b 2) ;(2) -x (2x-3) .
(1) ab (a2+b2)
=ab ·a 2+ab ·b 2
=a 3b+ab 3.
(2) -x (2x-3)
=(-x )×(2x )+ (-x )×(-3)
=-2x 2+3x.
解:
探索新知
总 结
单项式与多项式相乘时,依据法则将其转化为
单项式与单项式相乘,相乘每两项的积用“+”号
相连,然后按单项式与单项式相乘的法则逐个计算,
特别要注意符号.
典题精讲
1
计算:
(1) 8b 2(2a 2-ab-b 2); (2) ab 2 (3a -6b).
(1)8b 2(2a 2-ab-b 2)=8b 2·2a 2-8b 2·ab-8b 2·b 2
=16a 2b 2-8ab 3-8b 4.
(2) ab 2(3a-6b)= ab 2·3a- ab 2·6b
=2a 2b 2-4ab 3.
解:
典题精讲
计算:
(1)3x (4x 2y-2xy 2);
(2)3a (2a 2-a+2);
(3)(-2ab)2·(3a+2b-1);
(4) ·(-4x ).
2
典题精讲
(1)3x (4x 2y-2xy 2)=3x ·4x 2y-3x ·2xy 2=12x 3y-6x 2y 2.
(2)3a (2a 2-a+2)=3a ·2a 2-3a ·a+3a ·2=6a 3-3a 2+6a.
(3)(-2ab)2·(3a+2b-1)=4a 2b 2·(3a+2b-1)=4a 2b 2·3a+4a 2b 2·2b-4a 2b 2=12a 3b 2+8a 2b 3-4a 2b 2.
(4) ·(-4x)
= xy ·(-4x )- y ·(-4x )-y 2·(-4x )
=-3x 2y+2xy+4xy 2
解:
典题精讲
计算:
(1)a (a-b)+3b (a+4b);
(2)3a (a 2+3a-2)-3(a 3+2a 2-a+1) ;
(3)2x (-xy )2-x 2(x 2y 2-y 2).
3
典题精讲
(1)a (a-b)+3b (a+4b)=a 2-ab+3ab+12b 2=a 2+2ab+12b 2.
(2)3a (a 2+3a-2)-3(a 3+2a 2-a+1)=3a 3+9a 2-6a-3a 3-6a 2+3a-3=3a 2-3a-3.
(3)2x (-xy)2-x 2(x 2y 2-y 2)=2x ·x 2y 2-x 2(x 2y 2-y 2)=2x 3y 2-x 4y 2+x 2y 2.
解:
典题精讲
4
计算: 2ab (a 2b+ab-ab 2)-ab 2(a 2-2ab+2a)
2ab (a 2b+ab-ab 2)-ab 2(a 2-2ab+2a)=2ab ·a 2b+2ab ·ab-2ab ·ab 2-ab 2·a 2+
ab 2·2ab-ab 2·2a=2a 3b 2+2a 2b 2-2a 2b 3-a 3b 2+2a 2b 3-2a 2b 2=a 3b 2.
解:
典题精讲
计算6x ·(3-2x )的结果,与下列哪一个式子相同?( )
A.-12x 2+18x B.-12x 2+3
C.16x D.6x
下列运算正确的是( )
A.-2(a+b)=-2a+2b B.(a 2)3=a 5
C.a 3+4a= a 3 D.3a 2·2a 3=6a 5
5
A
D
6
典题精讲
下列运算错误的是( )
A.-m 2·m 3=-m 5
B.-x 2+2x 2=x 2
C.(-a 3b)2=a 6b 2
D.-2x (x-y )=-2x 2-2xy
如果一个长方形的周长为10,其中长为a,那么该长方形的面积为( )
A.10a B.5a-a 2
C.5a D.10a-a 2
7
D
8
B
探索新知
2
知识点
单项式与多项式相乘法则的应用
例3
先化简,再求值: a 2(a+1)-a (a 2-1).
其中,a=5.
a 2(a+1)-a (a 2-1)
=a 3+a 2-a 3+a
=a 2+a
当a=5时,原式=52+5=30
解:
探索新知
总 结
化简求值得题目,先化简再求值,化简的过程
包括整式的乘法与加减法运算,求值的过程就是直
接代入求值.
典题精讲
先化简,再求值: 2x (x-3y-1)+y (6x-y+2).
其中,x =-3,y =2.
1
2x (x-3y-1)+y (6x-y+2)=2x ·x-2x ·3y-2x+6xy-y ·y+2y=2x 2-2x-y 2+2y.
当x=-3,y=2时,原式=2×(-3)2-2×(-3)-22+2×2=18+6-4+4=24.
解:
典题精讲
先化简,再求值:
ab (ab-2a+2)-2b (a 2b-2ab+2a).其中,a=-1,b=-2.
2
ab (ab-2a+2)-2b (a 2b-2ab+2a)=ab ·ab-ab ·2a+ab ·2-2b ·a 2b+2b ·2ab-2b ·2a=a 2b 2-2a 2b+2ab-
2a 2b 2+4ab 2-4ab=-a 2b 2-2a 2b+4ab 2-2ab.
当a=-1,b=-2时,原式=-(-1)2×(-2)2-2×(-1)2
×(-2)+4×(-1)×(-2)2-2×(-1) ×(-2)=-4+4-16-4=-20.
解:
典题精讲
解方程: x (x-3)+2x (x+2)=3x 2-5.
3
去括号,得x 2-3x+2x 2+4x=3x 2-5.
移项,得x 2-3x+2x 2+4x-3x 2=-5.
合并同类项,得x=-5.
解:
典题精讲
计算下列物体的体积和表面积:
4
典题精讲
圆柱:体积V=πr 2·(3r+3)=3πr 3+3πr 2;
表面积S=2πr 2+2πr (3r+3)=2πr 2+6πr 2+6πr=8πr 2+6πr.
长方体:体积V=(4a-1)·a ·2a=8a 3-2a 2;
表面积S=2[2a ·(4a-1)+2a ·a+a ·(4a-1)]=2(8a 2-2a+2a 2+4a 2-a)=2(14a 2-3a)=
28a 2-6a.
解:
典题精讲
今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy (4y-2x-1)=-12xy 2+6x 2y+□,□的地方被钢笔水弄污了,你认为□内应填写( )
A.3xy B.-3xy
C.-1 D.1
5
A
典题精讲
要使x (x+a)+3x-2b=x 2+5x+4成立,则a,b 的值分别为( )
A.a=-2,b=-2 B.a=2,b=2
C.a=2,b=-2 D.a=-2,b=2
若计算(x 2+ax+5)·(-2x )-6x 2的结果中不含有x 2项,则a 的值为( )
A.-3 B.-
C.0 D.3
6
C
A
7
典题精讲
如图,通过计算大长方形的面积可得到的恒等式为________________________.
8
2a (a+b)=2a 2+2ab
典题精讲
化简:
(1)(-2ab)(3a 2-2ab-4b 2);
(2)3x (2x-3y )-(2x-5y ) ·4x;
(3)5a (a-b+c)-2b (a+b-c)-4c (-a-b-c ).
9
(1)原式=-6a 3b+4a 2b 2+8ab 3.
(2)原式=6x 2-9xy-8x 2+20xy=-2x 2+11xy.
(3)原式=5a 2-5ab+5ac-2ab-2b 2+2bc+4ac+4bc+4c 2=5a 2-2b 2+4c 2-7ab+9ac+6bc.
解:
典题精讲
先化简,再求值:3a (2a 2-4a+3)-2a 2(3a+4),
其中a=-2.
10
原式=6a 3-12a 2+9a-6a 3-8a 2=-20a 2+9a,
当a=-2时,原式=-20×4-9×2=-98.
解:
典题精讲
解方程:2x (x-1)=12+x (2x-5).
11
去括号,得2x 2-2x=12+2x 2-5x,
移项、合并同类项,得3x=12,
系数化为1,得x=4.
解:
易错提醒
下列运算中,正确的是( )
A.-2x (3x 2y-2xy )=-6x 3y-4x 2y
B.2xy 2(-x 2+2y 2+1)=-4x 3y 4
C.(3ab 2-2ab)·abc=3a 2b 3-2a 2b 2
D.(ab)2(2ab 2-c)=2a 3b 4-a 2b 2c
D
易错点:对单项式与多项式相乘的法则理解不透而出错
学以致用
小试牛刀
下列计算错误的是( )
A.-3x (2-x)=-6x+3x 2
B.(2m 2n-3mn 2)(-mn)=-2m 3n 2+3m 2n 3
C.xy (x 2y-xy 2-1)=x 3y 2-x 2y 3
D.
C
1
小试牛刀
2
计算:
小试牛刀
(1)原式=
(2)原式
解:
小试牛刀
3
先化简,再求值:
3(2x+1)+2(3-x ),其中x=-1.
原式=6x+3+6-2x
=4x+9.
当x=-1时,4x+9=4×(-1)+9=5.
解:
已知ab 2=-1,求(-ab)(a 2b 5-ab 3-b)的值.
原式=-a 3b 6+a 2b 4+ab 2=-(ab 2)3+(ab 2)2+ab 2.
当ab 2=-1时,原式=-(-1)3+(-1)2+(-1)=1.
解:
4
小试牛刀
某同学在计算一个多项式乘-3x 2时,算成了加上-3x 2,得到的答案是x 2- x+1,那么正确的计算结果是多少?
设这个多项式为A,则A+(-3x 2)=x 2- x+1,所以A=4x 2- x+1.
所以A ·(-3x 2)= ×(-3x 2)
=-12x 4+ x 3-3x 2.
解:
5
小试牛刀
6
当m,n 为何值时, x [x (x+m)+nx (x+1)+m] 的展开式中不含x 2项和x 3项?
x [x (x+m)+nx (x+1)+m]= x (x 2+mx+nx 2+nx+m)= (1+n)x 3+ (m+n)x 2+ mx,
因为它不含x 2项和x 3项,所以1+n=0,m+n=0,
解得n=-1,m=1.
解:
小试牛刀
7
一张长方形硬纸片,长为(5a 2+4b 2)m,宽为6a 4 m,在它的四个角上分别剪去一个边长为 a3 m的小正方形,然后折成一个无盖的盒子,请你求这个无盖盒子的表面积.
解:
纸片的面积是:(5a 2+4b 2)·6a 4=30a 6+24a 4b 2(m2),
小正方形的面积是: = a 6(m2),
则无盖盒子的表面积是:
30a 6+24a 4b 2-4× a 6=21a 6+24a 4b 2(m2).
课堂小结
课堂小结
1. 单项式与多项式相乘的依据是:乘法对加法的分配律.
2. 单项式与多项式相乘,其积仍是多项式,项数与原
多项式的项数 相同,注意不要漏乘项.
3. 积的每一项的符号由原多项式各项符号和单项式的
符号来决定,注意去括号法则.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
