【班海精品】冀教版(新)八下-19.4 坐标与图形的变化 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-19.4 坐标与图形的变化 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览







文档简介
(共47张PPT)
19.4 坐标与图形
的变化
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾反思
点的平移与点的坐标变化规律:
左、右平移,横变纵不变,“右加左减”;
上、下平移,纵变横不变,“上加下减”.
新课精讲
探索新知
知识点
用坐标表示图形的对称
1.关于x 轴成轴对称的两个图形,各对应顶点的横坐
标相等,纵坐标互为相反数.
2.关于y 轴成轴对称的两个图形,各对应顶点的纵坐
标相等,横坐标互为相反数.
1
探索新知
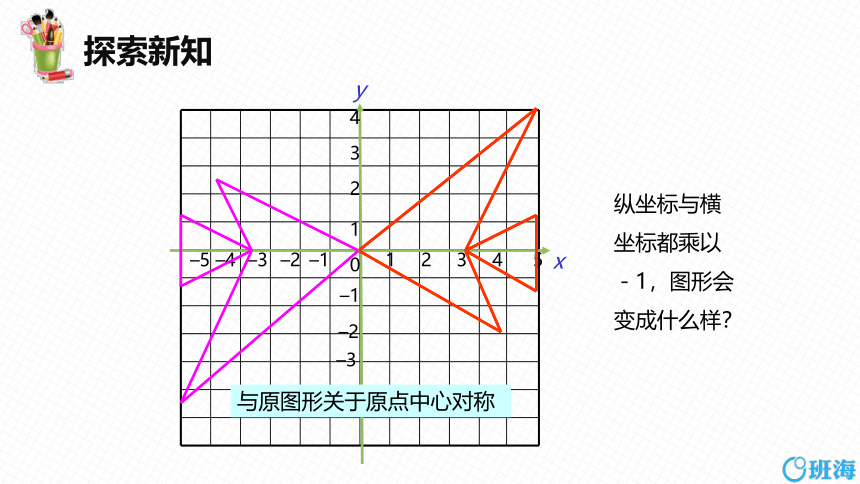
纵坐标与横坐标都乘以-1,图形会变成什么样?
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
–1
–2
–3
–4
–5
与原图形关于原点中心对称
探索新知
1
2
3
4
5
6
7
0
–1
–2
–3
–4
1
2
3
4
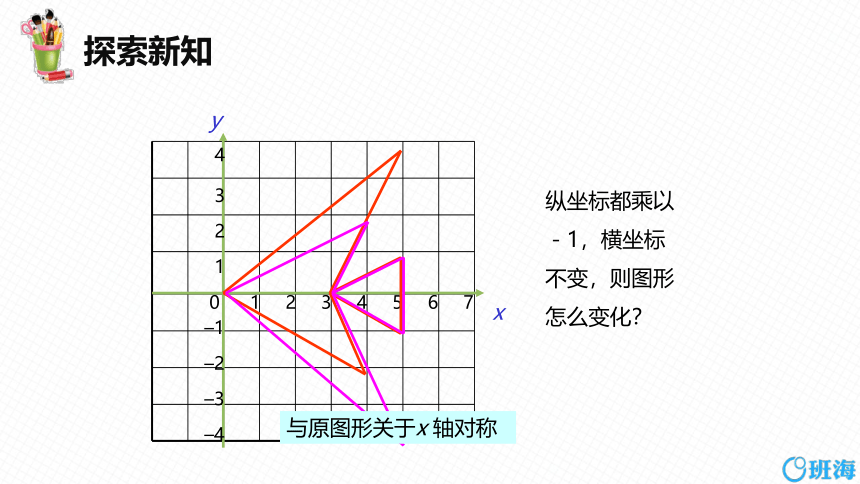
纵坐标都乘以-1,横坐标不变,则图形怎么变化?
y
x
与原图形关于x 轴对称
探索新知
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
1
2
3
4
-4
-5
5
y
x
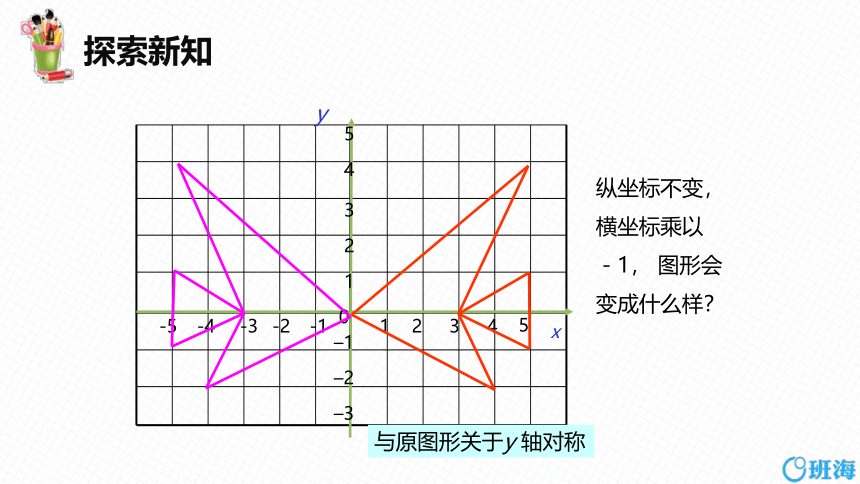
与原图形关于y 轴对称
纵坐标不变,横坐标乘以-1, 图形会变成什么样?
探索新知
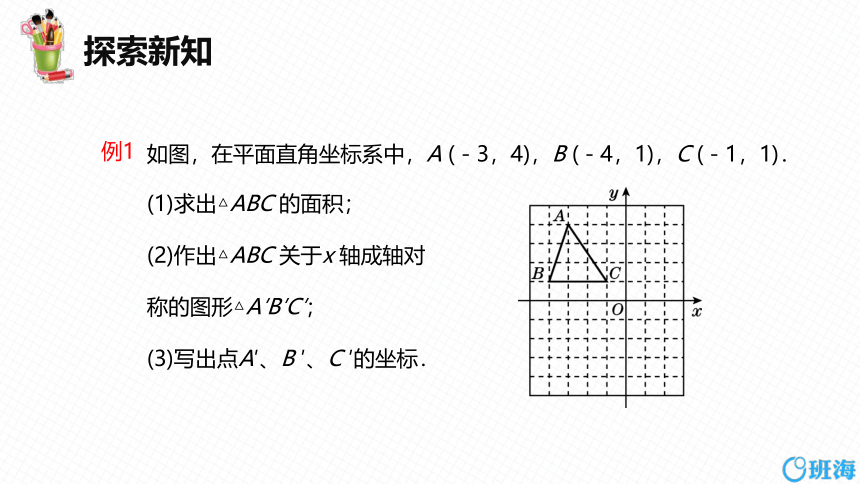
例1
如图,在平面直角坐标系中,A (-3,4),B (-4,1),C (-1,1).
(1)求出△ABC 的面积;
(2)作出△ABC 关于x 轴成轴对
称的图形△A′B′C′;
(3)写出点A′、B ′、C ′的坐标.
探索新知
(1)借助直角坐标系中的正方形网格,易判断△ABC
中,BC=3,BC上的高为3,据此可求出其面积;
(2)根据轴对称的性质可画出图形,或根据关于x 轴
成轴对称的点的坐标特点,先求出A、B、C 的对
应点的坐标,再描出这些点,顺次连接即可;
(3)根据关于x 轴成轴对称的两点的横坐标相等,纵
坐标互为相反数,可得点A ′、B ′、C ′的坐标.
导引:
探索新知
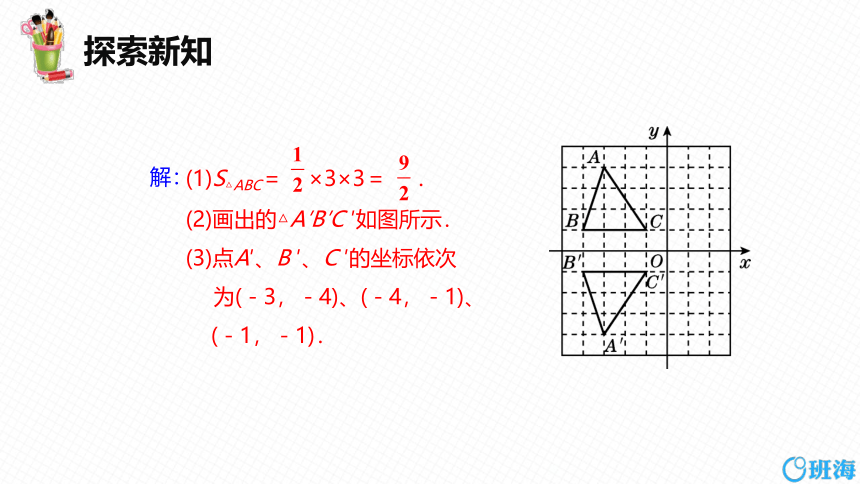
(1)S△ABC= ×3×3= .
(2)画出的△A′B′C ′如图所示.
(3)点A′、B ′、C ′的坐标依次
为(-3,-4)、(-4,-1)、
(-1,-1).
解:
探索新知
总 结
此题以带有网格的直角坐标系为背景,使面积的计算、轴对称作图及点的坐标的判断显得简单.
典题精讲
△ABC 在直角坐标系中的位置如图所示.
(1)作与△ABC 关于x 轴成轴对称的△A1B1C1 ,
并写出△A1B1C1各顶点的坐标.
(2)作与△ABC 关于y 轴成轴对称的
△A2B2C2,并与出△A2B2C2各顶点的坐标.
1
典题精讲
(1)△A1B1C1如图.
A1(2,-4),
B1(1,-1),
C1(3,-2).
(2)△A2B2C2如图.
A2(-2,4),
B2(-1,1),
C2(-3,2).
解:
典题精讲
如图,△ABC 与△DFE 关于y 轴对称,已知A (-4,6),B (-6,2),E (2,1),则点D 的坐标为( )
A.(-6,4)
B.(4,6)
C.(-2,1)
D.(6,2)
2
B
典题精讲
将一个图形各点的横坐标分别乘-1,纵坐标不变,所得的图形与原图形的关系是( )
A.关于x 轴对称
B.关于y 轴对称
C.关于第一、三象限的角平分线对称
D.无法确定
3
B
典题精讲
如图,△ABC 的顶点都在正方形网格格点上,点A 的坐标为(-1,4),将△ABC 沿y 轴翻折到第一象限,则点C 的对应点C ′的坐标是( )
A.(3,1)
B.(-3,-1)
C.(1,-3)
D.(3,-1)
4
A
探索新知
2
知识点
用坐标表示图形的放缩
将一个图形各顶点的横坐标和纵坐标都乘k
(或 ,k>1),所得图形的形状不变,各边扩大
到原来的k 倍(或缩小为原来的 ),且连接各对
应顶点的直线相交于一点.
探索新知
x
y
0
A’(10,4)
D'
C’
E’(8,-2)
B’
E(4,-2)
A(5,4)
D(5,-1)
C(5,1)
B(3,0)
纵坐标保持不变,横坐标分别变成原来的2倍.
探索新知
1
2
3
4
5
6
0
–1
–2
–3
1
2
3
4
5
纵坐标不变, 横坐标变成原来的 ,图形会怎么变?
x
原图形被横向压缩
探索新知
如图所示,正方形ABCD 四个顶点A,B,C,D 的坐标分别是(1,1),(-1,1),(-1,-1),(1,-1).
(1)试求正方形ABCD 各顶点
横、纵坐标都乘以2后所
得的正方形的面积;
(2)试求正方形ABCD 各顶点
横坐标不变,纵坐标都乘
以2后得到的长方形的面积.
例2
探索新知
根据图形的放缩与坐标变化的关系判断当图形中各点坐标发生变化后,图形发生了怎样的变化,来确定图形的边长,从而确定图形的面积.
导引:
(1)变换后的正方形A1B1C1D1
如图所示,
显然A1B1=B1C1=C1D1
=D1A1=2×2=4,
所以S 正方形A1B1C1D1=A1B12=42=16.
解:
探索新知
(2)变换后的长方形A2B2C2D2如图所示,
显然A2B2=C2D2=2,B2C2=A2D2=4,
所以S长方形A2B2C2D2=A2B2×B2C2=2×4=8.
探索新知
总 结
图形的平移只改变图形的位置,而不改变图形的形状和大小,将图形的坐标都乘或除以同一个不为0的数时,图形的形状没有改变,但大小可能发生了改变.
典题精讲
1
已知△ABC 的顶点坐标分别为A (0,0),B (6,0),C (3,4.5),
△A1B1C1的顶点坐标分别为A1(0,0),B1(12,0),C1(6,9),△A2B2C2的顶点坐标分别为A2(0,0),B2(4,0),C2(2,3).
(1) △A1B1C1与△ABC 的形状和大小各有什么关系?
(2) △A2B2C2与△ABC 的形状和大小各有什么关系?
典题精讲
(1)△A1B1C1与△ABC 的形状相同,各边长是△ABC 对应边长的2倍.
(2)△A2B2C2与△ABC 的形状相同,各边长是△ABC 对应边长的 .
解:
典题精讲
将某个图形上各点的横、纵坐标都乘 ,所得图形与原图形相比( )
A.完全没有变化
B.边长扩大为原来的2倍
C.边长缩小为原来的
D.关于纵轴成轴对称
2
C
典题精讲
将平面直角坐标系内某个图形各个点的横坐标、纵坐标都乘3,所得图形的面积( )
A.是原图形的3倍
B.是原图形的9倍
C.不变
D.是原图形的6倍
3
B
易错提醒
如图,△ABC 经过两次轴对称(x 轴和y 轴为对称轴)变化后,得到△DEF,如果A,B,C 各点的坐标分别为A (-5,1),B (-2,0),
C (1,3),那么D,E,F 各点
的坐标分别为D ,
E________,F .
易错点:易混淆多次轴对称的坐标变化而致错.
(5,-1)
(2,0)
(-1,-3)
学以致用
小试牛刀
下列图形中,将图形上各点的纵坐标保持不变,横坐标分别乘-1后,图形一定不发生变化的是( )
①圆心在原点的圆;
②两条对角线的交点在原点的正方形;
③以y轴为对称轴的等腰三角形;
④以x轴为对称轴的等腰三角形.
A.①②③④ B.①②③
C.①③ D.②④
C
1
小试牛刀
如图,在平面直角坐标系中,四边形ABCD 的各顶点坐标分别是A (1,0),B (2,0),C (2,2),D (0,1),四边形BFGH 的各顶点坐标分别是B (2,0),F (4,0),G (4,4),H (0,2).
有下列说法:①四边形ABCD 与四边形BFGH 的形状相同;
②CD:GH=1:2;
③CD:GH=1: ;
④连接各对应顶点的直线相交于一点.
其中说法正确的有( )
A.1个 B.2个
C.3个 D.4个
C
2
小试牛刀
3
如图,在直角坐标系中,△ABC 的三个顶点的坐标分别为A (1,1),B (3,4),C (5,2).
(1)作出△ABC 关于x 轴的对称图形△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(1)如图.
(2)A1(1,-1),
B1(3,-4),
C1(5,-2).
解:
小试牛刀
(3)S△ABC= ×(1+4)×2+ ×(2+4)×2
- ×(1+2)×4
=5.
解:
(3)求△ABC 的面积.
小试牛刀
4
如图,△ABC 的顶点均在格点上.
(1)写出A,B,C 三点的坐标.
(1)A(3,4),
B (1,2),
C (5,1).
解:
小试牛刀
(2)若△ABC 各顶点的纵坐标不变,横坐标都乘-1,请你在同一坐标系中描出对应点A′,B ′,C ′,并依次连接这三个点,所得的△A′B′C ′与△ABC 有怎样的位置关系?
(3)求△ABC 的面积.
(2)图略.△A′B′C ′与△ABC 关于y 轴对称.
(3)S△ABC=3×4- ×2×2- ×2×3- ×1×4
=5.
解:
小试牛刀
5
在直角坐标系中描出下列各点:
A (-3,0),B (9,0),C (12,6),D (0,6).
(1)把点A,B,C,D,A 顺次连接,组成封闭图形.
点A,B,C,D 如图.
(1)如图所示
解:
小试牛刀
(2)如果各顶点的横坐标不变,纵坐标乘3,将新得
到的顶点依次连接成封闭图形,那么新的图形
与(1)中图形的形状相比,有怎样的变化?
(2)对应的新顶点的坐标分别为A′(-3,0),B ′(9,0),
C ′(12,18),D ′(0,18),画图略.新图形是由(1)
中的图形纵向扩大为原来的3倍得到的.
解:
小试牛刀
(3)如果各顶点的横坐标乘 ,纵坐标不变,将新
得到的顶点依次连接成封闭图形,那么新的图形
与(1)中图形的形状相比,有怎样的变化?
(3)对应的新顶点的坐标分别为A″(-1,0),B ″(3,0),
C ″(4,6),D ″(0,6),画图略.
新图形是由(1)中的图形横向缩小为原来的 得到的.
解:
小试牛刀
(4)如果各顶点的横、纵坐标都乘 ,将新得到的
顶点依次连接成封闭图形,那么新的图形与(1)
中图形的形状相比,有怎样的变化?
(4)对应的新顶点的坐标分别为A1(-1,0),B1(3,0),
C1(4,2),D1(0,2),画图略.
新图形是由(1)中的图形横向和纵向同时缩小为原
来的 得到的.
解:
小试牛刀
6
如图,正方形ABCD 四个顶点的坐标分别是A (1,1),B (1,-1),C (-1,-1),D (-1,1).求将正方形ABCD 各顶点的横、纵坐标都乘2后得到的正方形的面积.
小试牛刀
解:新正方形是将原正方形放大2倍得到的,故新正方形的面积等于原正方形面积的2倍,所以新正方形的面积=2×(2×2)=8.
上面的解答正确吗?如果不正确,请你写出正确的解答过程.
不正确.
设将正方形ABCD 各顶点的横、纵坐标都乘2后得到正方形A′B′C′D ′,则A′(2,2),B ′(2,-2),C ′(-2,-2),D ′(-2,2),∴正方形A′B′C′D ′的边长为4,面积为4×4=16. ∴新正方形的面积为16.
解:
课堂小结
课堂小结
图形在对称前后点的坐标变化情况:
(1)关于x 轴对称的两个图形,各对应点的横坐标相
等,纵坐标互为相反数;
(2)关于y 轴对称的两个图形,各对应点的横坐标互
为相反数,纵坐标相等;
(3)关于原点对称的两个图形,各对应点的横、纵
坐标都互为相反数.
课堂小结
在坐标系中作成轴对称的图形的方法:
(1)确定对称点的坐标;
(2)根据对称点的坐标描点;
(3)依次连接所描的点得到成轴对称的图形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
19.4 坐标与图形
的变化
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾反思
点的平移与点的坐标变化规律:
左、右平移,横变纵不变,“右加左减”;
上、下平移,纵变横不变,“上加下减”.
新课精讲
探索新知
知识点
用坐标表示图形的对称
1.关于x 轴成轴对称的两个图形,各对应顶点的横坐
标相等,纵坐标互为相反数.
2.关于y 轴成轴对称的两个图形,各对应顶点的纵坐
标相等,横坐标互为相反数.
1
探索新知
纵坐标与横坐标都乘以-1,图形会变成什么样?
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
–1
–2
–3
–4
–5
与原图形关于原点中心对称
探索新知
1
2
3
4
5
6
7
0
–1
–2
–3
–4
1
2
3
4
纵坐标都乘以-1,横坐标不变,则图形怎么变化?
y
x
与原图形关于x 轴对称
探索新知
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
1
2
3
4
-4
-5
5
y
x
与原图形关于y 轴对称
纵坐标不变,横坐标乘以-1, 图形会变成什么样?
探索新知
例1
如图,在平面直角坐标系中,A (-3,4),B (-4,1),C (-1,1).
(1)求出△ABC 的面积;
(2)作出△ABC 关于x 轴成轴对
称的图形△A′B′C′;
(3)写出点A′、B ′、C ′的坐标.
探索新知
(1)借助直角坐标系中的正方形网格,易判断△ABC
中,BC=3,BC上的高为3,据此可求出其面积;
(2)根据轴对称的性质可画出图形,或根据关于x 轴
成轴对称的点的坐标特点,先求出A、B、C 的对
应点的坐标,再描出这些点,顺次连接即可;
(3)根据关于x 轴成轴对称的两点的横坐标相等,纵
坐标互为相反数,可得点A ′、B ′、C ′的坐标.
导引:
探索新知
(1)S△ABC= ×3×3= .
(2)画出的△A′B′C ′如图所示.
(3)点A′、B ′、C ′的坐标依次
为(-3,-4)、(-4,-1)、
(-1,-1).
解:
探索新知
总 结
此题以带有网格的直角坐标系为背景,使面积的计算、轴对称作图及点的坐标的判断显得简单.
典题精讲
△ABC 在直角坐标系中的位置如图所示.
(1)作与△ABC 关于x 轴成轴对称的△A1B1C1 ,
并写出△A1B1C1各顶点的坐标.
(2)作与△ABC 关于y 轴成轴对称的
△A2B2C2,并与出△A2B2C2各顶点的坐标.
1
典题精讲
(1)△A1B1C1如图.
A1(2,-4),
B1(1,-1),
C1(3,-2).
(2)△A2B2C2如图.
A2(-2,4),
B2(-1,1),
C2(-3,2).
解:
典题精讲
如图,△ABC 与△DFE 关于y 轴对称,已知A (-4,6),B (-6,2),E (2,1),则点D 的坐标为( )
A.(-6,4)
B.(4,6)
C.(-2,1)
D.(6,2)
2
B
典题精讲
将一个图形各点的横坐标分别乘-1,纵坐标不变,所得的图形与原图形的关系是( )
A.关于x 轴对称
B.关于y 轴对称
C.关于第一、三象限的角平分线对称
D.无法确定
3
B
典题精讲
如图,△ABC 的顶点都在正方形网格格点上,点A 的坐标为(-1,4),将△ABC 沿y 轴翻折到第一象限,则点C 的对应点C ′的坐标是( )
A.(3,1)
B.(-3,-1)
C.(1,-3)
D.(3,-1)
4
A
探索新知
2
知识点
用坐标表示图形的放缩
将一个图形各顶点的横坐标和纵坐标都乘k
(或 ,k>1),所得图形的形状不变,各边扩大
到原来的k 倍(或缩小为原来的 ),且连接各对
应顶点的直线相交于一点.
探索新知
x
y
0
A’(10,4)
D'
C’
E’(8,-2)
B’
E(4,-2)
A(5,4)
D(5,-1)
C(5,1)
B(3,0)
纵坐标保持不变,横坐标分别变成原来的2倍.
探索新知
1
2
3
4
5
6
0
–1
–2
–3
1
2
3
4
5
纵坐标不变, 横坐标变成原来的 ,图形会怎么变?
x
原图形被横向压缩
探索新知
如图所示,正方形ABCD 四个顶点A,B,C,D 的坐标分别是(1,1),(-1,1),(-1,-1),(1,-1).
(1)试求正方形ABCD 各顶点
横、纵坐标都乘以2后所
得的正方形的面积;
(2)试求正方形ABCD 各顶点
横坐标不变,纵坐标都乘
以2后得到的长方形的面积.
例2
探索新知
根据图形的放缩与坐标变化的关系判断当图形中各点坐标发生变化后,图形发生了怎样的变化,来确定图形的边长,从而确定图形的面积.
导引:
(1)变换后的正方形A1B1C1D1
如图所示,
显然A1B1=B1C1=C1D1
=D1A1=2×2=4,
所以S 正方形A1B1C1D1=A1B12=42=16.
解:
探索新知
(2)变换后的长方形A2B2C2D2如图所示,
显然A2B2=C2D2=2,B2C2=A2D2=4,
所以S长方形A2B2C2D2=A2B2×B2C2=2×4=8.
探索新知
总 结
图形的平移只改变图形的位置,而不改变图形的形状和大小,将图形的坐标都乘或除以同一个不为0的数时,图形的形状没有改变,但大小可能发生了改变.
典题精讲
1
已知△ABC 的顶点坐标分别为A (0,0),B (6,0),C (3,4.5),
△A1B1C1的顶点坐标分别为A1(0,0),B1(12,0),C1(6,9),△A2B2C2的顶点坐标分别为A2(0,0),B2(4,0),C2(2,3).
(1) △A1B1C1与△ABC 的形状和大小各有什么关系?
(2) △A2B2C2与△ABC 的形状和大小各有什么关系?
典题精讲
(1)△A1B1C1与△ABC 的形状相同,各边长是△ABC 对应边长的2倍.
(2)△A2B2C2与△ABC 的形状相同,各边长是△ABC 对应边长的 .
解:
典题精讲
将某个图形上各点的横、纵坐标都乘 ,所得图形与原图形相比( )
A.完全没有变化
B.边长扩大为原来的2倍
C.边长缩小为原来的
D.关于纵轴成轴对称
2
C
典题精讲
将平面直角坐标系内某个图形各个点的横坐标、纵坐标都乘3,所得图形的面积( )
A.是原图形的3倍
B.是原图形的9倍
C.不变
D.是原图形的6倍
3
B
易错提醒
如图,△ABC 经过两次轴对称(x 轴和y 轴为对称轴)变化后,得到△DEF,如果A,B,C 各点的坐标分别为A (-5,1),B (-2,0),
C (1,3),那么D,E,F 各点
的坐标分别为D ,
E________,F .
易错点:易混淆多次轴对称的坐标变化而致错.
(5,-1)
(2,0)
(-1,-3)
学以致用
小试牛刀
下列图形中,将图形上各点的纵坐标保持不变,横坐标分别乘-1后,图形一定不发生变化的是( )
①圆心在原点的圆;
②两条对角线的交点在原点的正方形;
③以y轴为对称轴的等腰三角形;
④以x轴为对称轴的等腰三角形.
A.①②③④ B.①②③
C.①③ D.②④
C
1
小试牛刀
如图,在平面直角坐标系中,四边形ABCD 的各顶点坐标分别是A (1,0),B (2,0),C (2,2),D (0,1),四边形BFGH 的各顶点坐标分别是B (2,0),F (4,0),G (4,4),H (0,2).
有下列说法:①四边形ABCD 与四边形BFGH 的形状相同;
②CD:GH=1:2;
③CD:GH=1: ;
④连接各对应顶点的直线相交于一点.
其中说法正确的有( )
A.1个 B.2个
C.3个 D.4个
C
2
小试牛刀
3
如图,在直角坐标系中,△ABC 的三个顶点的坐标分别为A (1,1),B (3,4),C (5,2).
(1)作出△ABC 关于x 轴的对称图形△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(1)如图.
(2)A1(1,-1),
B1(3,-4),
C1(5,-2).
解:
小试牛刀
(3)S△ABC= ×(1+4)×2+ ×(2+4)×2
- ×(1+2)×4
=5.
解:
(3)求△ABC 的面积.
小试牛刀
4
如图,△ABC 的顶点均在格点上.
(1)写出A,B,C 三点的坐标.
(1)A(3,4),
B (1,2),
C (5,1).
解:
小试牛刀
(2)若△ABC 各顶点的纵坐标不变,横坐标都乘-1,请你在同一坐标系中描出对应点A′,B ′,C ′,并依次连接这三个点,所得的△A′B′C ′与△ABC 有怎样的位置关系?
(3)求△ABC 的面积.
(2)图略.△A′B′C ′与△ABC 关于y 轴对称.
(3)S△ABC=3×4- ×2×2- ×2×3- ×1×4
=5.
解:
小试牛刀
5
在直角坐标系中描出下列各点:
A (-3,0),B (9,0),C (12,6),D (0,6).
(1)把点A,B,C,D,A 顺次连接,组成封闭图形.
点A,B,C,D 如图.
(1)如图所示
解:
小试牛刀
(2)如果各顶点的横坐标不变,纵坐标乘3,将新得
到的顶点依次连接成封闭图形,那么新的图形
与(1)中图形的形状相比,有怎样的变化?
(2)对应的新顶点的坐标分别为A′(-3,0),B ′(9,0),
C ′(12,18),D ′(0,18),画图略.新图形是由(1)
中的图形纵向扩大为原来的3倍得到的.
解:
小试牛刀
(3)如果各顶点的横坐标乘 ,纵坐标不变,将新
得到的顶点依次连接成封闭图形,那么新的图形
与(1)中图形的形状相比,有怎样的变化?
(3)对应的新顶点的坐标分别为A″(-1,0),B ″(3,0),
C ″(4,6),D ″(0,6),画图略.
新图形是由(1)中的图形横向缩小为原来的 得到的.
解:
小试牛刀
(4)如果各顶点的横、纵坐标都乘 ,将新得到的
顶点依次连接成封闭图形,那么新的图形与(1)
中图形的形状相比,有怎样的变化?
(4)对应的新顶点的坐标分别为A1(-1,0),B1(3,0),
C1(4,2),D1(0,2),画图略.
新图形是由(1)中的图形横向和纵向同时缩小为原
来的 得到的.
解:
小试牛刀
6
如图,正方形ABCD 四个顶点的坐标分别是A (1,1),B (1,-1),C (-1,-1),D (-1,1).求将正方形ABCD 各顶点的横、纵坐标都乘2后得到的正方形的面积.
小试牛刀
解:新正方形是将原正方形放大2倍得到的,故新正方形的面积等于原正方形面积的2倍,所以新正方形的面积=2×(2×2)=8.
上面的解答正确吗?如果不正确,请你写出正确的解答过程.
不正确.
设将正方形ABCD 各顶点的横、纵坐标都乘2后得到正方形A′B′C′D ′,则A′(2,2),B ′(2,-2),C ′(-2,-2),D ′(-2,2),∴正方形A′B′C′D ′的边长为4,面积为4×4=16. ∴新正方形的面积为16.
解:
课堂小结
课堂小结
图形在对称前后点的坐标变化情况:
(1)关于x 轴对称的两个图形,各对应点的横坐标相
等,纵坐标互为相反数;
(2)关于y 轴对称的两个图形,各对应点的横坐标互
为相反数,纵坐标相等;
(3)关于原点对称的两个图形,各对应点的横、纵
坐标都互为相反数.
课堂小结
在坐标系中作成轴对称的图形的方法:
(1)确定对称点的坐标;
(2)根据对称点的坐标描点;
(3)依次连接所描的点得到成轴对称的图形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
