【班海精品】冀教版(新)八下-21.1 一次函数 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-21.1 一次函数 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览











文档简介
(共38张PPT)
21.1 一次函数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
函数可以用来刻画数景之间的关系,一次函数是一
种重要的函数. 现在,我们来探究一次函数.
新课精讲
探索新知
1
知识点
一次函数的定义
在本节“小刚骑自行车去上学”的问题中,小
刚家到学校的路程为3.5 km,小刚骑车的速度为
0.2 km/min.设小刚距学校的路程为s km,离开家的
时间为t min.
探索新知
一起探究
(1)写出s 与t 之间的函数关系式,并指出其中的常量与变量.
(2)写出t 的取值范围.
(3)对比正比例函数,它们的表达式在结构上有什么相同点与不同点?
探索新知
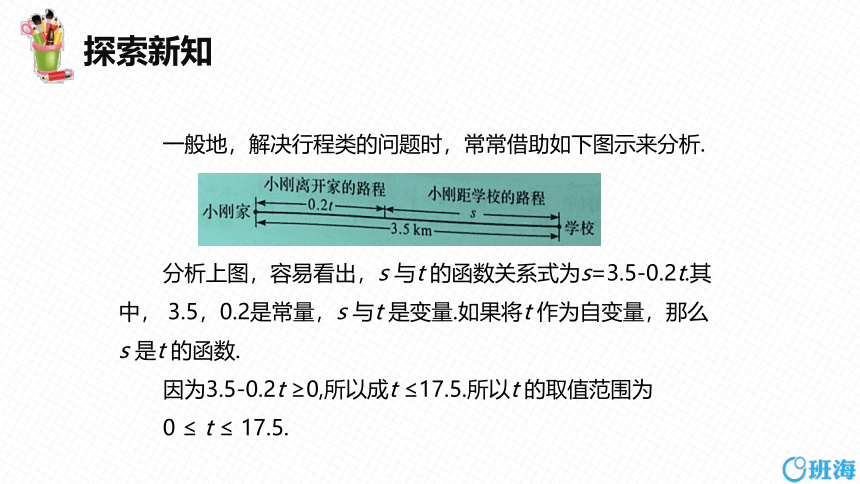
一般地,解决行程类的问题时,常常借助如下图示来分析.
分析上图,容易看出,s 与t 的函数关系式为s=3.5-0.2t.其中, 3.5,0.2是常量,s 与t 是变量.如果将t 作为自变量,那么s 是t 的函数.
因为3.5-0.2t ≥0,所以成t ≤17.5.所以t 的取值范围为
0 ≤ t ≤ 17.5.
探索新知
1. 某新建住宅小区的物业管理费按住房面积收缴,每月1.60元/平方米;有汽车的房主再交车库使用费,每月80元.设有车房主的住房面积为x m2, 每月应缴物业管理费与车库使用费的总和为y 元,则用x 表示y 的函数表达式为______________.
2. 向一个已装有10 dm3水的容器中再注水,注水速度
为2 dm3/min.容器内的水量y (dm3)与注水时间x(min)
的函数关系式为______________.
探索新知
3. 一种计算成年人标准体重G (kg)的方法是,以厘米为单位量出身高值h,减常数105,所得差是G 的值.用h 表示G 的函数表达式为______________.
从上面问题中,我们分别得到了函数表达式:
s=3.5-0.2t,y=1.6x+80,y=2x+10,G=h-105.
这些函数表达式的形式有什么共同特点?与同学交流你的看法.
探索新知
一般地,我们把形如y=kx+b (k,b为常数,且k≠0)的
函数,叫做一次函数.
对于一次函数; y=kx+b,当b=0时,它就化为y=kx.
所以正比例函数y=kx 是一次函数的特殊形式.
探索新知
例1 下列函数中,哪些是一次函数,哪些是正比例函数?
(1)y=-2x 2; (2)y= ;
(3)y=3x 2-x (3x-2);
(4)x 2+y=1; (5)y=- .
导引:先看函数表达式是否为整式,再通过恒等变形进行化简,然后根据一次函数和正比例函数的定义进行判断.
探索新知
解:(1)因为x 的次数是2,所以y=-2x 2不是一次函数.
(2)因为y= = x+ ,k= ≠0,b= ,所以
y= 是一次函数,但不是正比例函数.
(3)因为y=3x 2-x (3x-2)=2x,k=2,b=0,所以它
是一次函数,也是正比例函数.
(4)x 2+y=1,即y=1-x 2.因为x 的次数是2,所以x 2+y
=1不是一次函数.
(5)因为y=- 中 不是整式,不符合y=kx+b 的形
式,所以它不是一次函数.
探索新知
总 结
判断函数是否为一次函数的方法:先看函数表达式是否是整式,再将函数表达式进行恒等变形,然后看它是否符合一次函数表达式y=kx+b 的特征:(1)k≠0;(2)自变量x 的次数为1;(3)常数项b 可以为任意实数.
典题精讲
1 在下列函数中,哪些是一次函数?请指出一次函数中的k 和b 的值.
(1) y=2-x, (2) (3) s=8+0.03t,
(4) (5) (6)
解:(1)(3)(4)(5)是一次函数.(1)中k=-1,b=2;(3)中的k=0.03,b=8;(4)中的k= ,b=0;
(5)中的k= ,b=-3.
典题精讲
在下列函数中,哪些是一次函数?请指出一次函数中的k 和b 的值.
解:(1)(2)(4)是一次函数.(1)中的k=-1,b= ;
(2)中的k=2π,b=0;(4)中的k=0.5,b= .
典题精讲
3 下列函数中,y 是x 的一次函数的是( )
A.y=x 2+2x B.y=-
C.y=x D.y= +1
下列函数:①y=2x-1;②y=πx;③y= ;
④y=x 2中,一次函数的个数是( )
A.1 B.2 C.3 D.4
C
B
典题精讲
5 已知y=(m-3)x |m |-2+1是y 关于x 的一次函数,则m的值是( )
A.-3 B.3 C.±3 D.±2
6 若3y-4与2x-5成正比例,则y 是x 的( )
A.正比例函数 B.一次函数
C.没有函数关系 D.以上均不正确
A
B
探索新知
例2 已知关于x 的函数y=(2m-1)x+1-3m,当m满足什么条件时,
(1)这个函数是正比例函数?
(2)这个函数为一次函数?
导引:根据正比例函数和一次函数的定义求解即可.
探索新知
解:(1)∵函数y=(2m-1)x+1-3m 是正比例函数,∴1-3m=0,2m-1≠0,∴m= .∴当m= 时,这个函数是正比例函数.
(2)∵函数y=(2m-1)x+1-3m 是一次函数,
∴2m-1≠0,解得m≠ .∴当m≠ 时,这个函数为一次函数.
探索新知
总 结
一次函数y=kx+b 中k、b 为常数,k≠0,自变量
的次数为1.当b=0时,一次函数y=kx+b 就化为正比
例函数y=kx.
典题精讲
1 已知一次函数y =-2x +3.
(1) 当x 为何值时,y=0?
(2) 当y 为何值时,x=0?
解: (1)对于一次函数y=-2x+3,令y=0,
即-2x+3=0,解得x= .所以当x= 时,y=0.
(2)将x=0代入y=-2x+3中,得y=-2×0+3=3.
所以当y=3时,x=0.
探索新知
2
知识点
确定应用问题中的一次函数表达式
当“条件”中明确是一次函数关系时,可利用关系式y=kx+b 求解,依据已知求得k、b 的值就可以了;当“条件”中未明确是一次函数关系时(一般情况是实际应用题),我们应依据已知中的基本数量列出等量关系(类似列方程解应用题),再整理成y=kx+b (k,b 为常数,k≠0)的形式.
注意:在列出有关实际问题的一次函数关系式时,应标注自变量的取值范围.
探索新知
例3 如图所示, △ABC 是边长为x 的等边三角形.
(1)求BC 边上的高h 与x 之间的函数关系式. h 是x 的一次函数吗?如果是一次函数,请指出相应的k 与b 的值.
(2) 当h= 时,求x 的值.
(3)求△ABC 的面积S 与x 之间的函数
关系式. S 是x 的一次函数吗?
探索新知
解:(1)因为BC 边上的高AD 也是BC 边上的中线,所以
BD= .在Rt△ABD 中,由勾股定理,得
即
所以h 是x 的一次函数,且 .
探索新知
(2)当 时,有 .
解得x =2.
(3)因为
即 所以S 不是x 的一次函数.
典题精讲
已知两条平行线l1,l2 之间的距离为3 cm,点A 在l1 上,点B,C 在l2 上,BC=x. 求△ABC 的面积S 与x的函数关系式,并判断这个函数是不是一次函数.
解: S= ·BC · 3= x,这个函数是一次函数.
典题精讲
2 一个正方形的边长为3 cm,它的各边边长均减少x cm后,得到的新正方形的周长为y cm,y 与x 之间的函数表达式是( )
A.y=12-4x B.y=4x-12
C.y=12-x D.以上都不对
A
学以致用
小试牛刀
1 下列说法正确的是( )
A.正比例函数是一次函数
B.一次函数是正比例函数
C.对于变量x 与y,y 是x 的函数,x 不是y 的函数
D.正比例函数不是一次函数,一次函数也不是正比例函数
A
2 如图,图像表示的一次函数表达式为( )
A.y=-x-5
B.y=x-5
C.y=x+5
D.y=-x+5
小试牛刀
D
小试牛刀
3
我们知道,海拔高度每上升1千米,温度下降6 ℃.某时刻,益阳地面温度为20 ℃,设高出地面x 千米处的温度为y ℃.
(1)写出y 与x 之间的函数关系式;
(2)已知益阳碧云峰高出地面约500米,求这时山顶的温度大约是多少?
(3)此刻,有一架飞机飞过益阳上空,若机舱内仪表显示飞机外面的温度为-34 ℃,求飞机离地面的高度为多少千米?
小试牛刀
(1)y=20-6x (x>0).
(2)500米=0.5千米,当x=0.5时,y=20-6×0.5=17.
即这时山顶的温度大约为17 ℃.
(3)当y=-34时,有-34=20-6x,解得x=9.
即飞机离地面的高度为9千米.
解:
小试牛刀
4
学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人,如图所示,请你结合这个规律,填写下表并回答问题:
(1)写出y 与x 之间的函数解析式,并判断y 是不是x 的一次函数;
(2)若八年级(1)班有42人去阅览室看书,则需要多少张这样的方桌拼成一行?
拼成一行的方桌数(x ) 1 2 3 4 …
人数(y ) 4 6 8 …
10
小试牛刀
(1)y=2x+2,y 是x 的一次函数.
(2)把y=42代入y=2x+2中,
得42=2x+2,
解得x=20.
答:需要20张这样的方桌拼成一行.
解:
课堂小结
课堂小结
正比例函数与一次函数的关系
正比例函数是一次函数的特例,一次函数包括正比
例函数,用图形表示它们之
间的关系如图所示:
一次函数y=kx+b (k≠0) ,当b=0时是特殊的一次函数(即正比例函数),当b ≠ 0时是一般的一次函数.
一次函数
正比例函数
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
21.1 一次函数
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
函数可以用来刻画数景之间的关系,一次函数是一
种重要的函数. 现在,我们来探究一次函数.
新课精讲
探索新知
1
知识点
一次函数的定义
在本节“小刚骑自行车去上学”的问题中,小
刚家到学校的路程为3.5 km,小刚骑车的速度为
0.2 km/min.设小刚距学校的路程为s km,离开家的
时间为t min.
探索新知
一起探究
(1)写出s 与t 之间的函数关系式,并指出其中的常量与变量.
(2)写出t 的取值范围.
(3)对比正比例函数,它们的表达式在结构上有什么相同点与不同点?
探索新知
一般地,解决行程类的问题时,常常借助如下图示来分析.
分析上图,容易看出,s 与t 的函数关系式为s=3.5-0.2t.其中, 3.5,0.2是常量,s 与t 是变量.如果将t 作为自变量,那么s 是t 的函数.
因为3.5-0.2t ≥0,所以成t ≤17.5.所以t 的取值范围为
0 ≤ t ≤ 17.5.
探索新知
1. 某新建住宅小区的物业管理费按住房面积收缴,每月1.60元/平方米;有汽车的房主再交车库使用费,每月80元.设有车房主的住房面积为x m2, 每月应缴物业管理费与车库使用费的总和为y 元,则用x 表示y 的函数表达式为______________.
2. 向一个已装有10 dm3水的容器中再注水,注水速度
为2 dm3/min.容器内的水量y (dm3)与注水时间x(min)
的函数关系式为______________.
探索新知
3. 一种计算成年人标准体重G (kg)的方法是,以厘米为单位量出身高值h,减常数105,所得差是G 的值.用h 表示G 的函数表达式为______________.
从上面问题中,我们分别得到了函数表达式:
s=3.5-0.2t,y=1.6x+80,y=2x+10,G=h-105.
这些函数表达式的形式有什么共同特点?与同学交流你的看法.
探索新知
一般地,我们把形如y=kx+b (k,b为常数,且k≠0)的
函数,叫做一次函数.
对于一次函数; y=kx+b,当b=0时,它就化为y=kx.
所以正比例函数y=kx 是一次函数的特殊形式.
探索新知
例1 下列函数中,哪些是一次函数,哪些是正比例函数?
(1)y=-2x 2; (2)y= ;
(3)y=3x 2-x (3x-2);
(4)x 2+y=1; (5)y=- .
导引:先看函数表达式是否为整式,再通过恒等变形进行化简,然后根据一次函数和正比例函数的定义进行判断.
探索新知
解:(1)因为x 的次数是2,所以y=-2x 2不是一次函数.
(2)因为y= = x+ ,k= ≠0,b= ,所以
y= 是一次函数,但不是正比例函数.
(3)因为y=3x 2-x (3x-2)=2x,k=2,b=0,所以它
是一次函数,也是正比例函数.
(4)x 2+y=1,即y=1-x 2.因为x 的次数是2,所以x 2+y
=1不是一次函数.
(5)因为y=- 中 不是整式,不符合y=kx+b 的形
式,所以它不是一次函数.
探索新知
总 结
判断函数是否为一次函数的方法:先看函数表达式是否是整式,再将函数表达式进行恒等变形,然后看它是否符合一次函数表达式y=kx+b 的特征:(1)k≠0;(2)自变量x 的次数为1;(3)常数项b 可以为任意实数.
典题精讲
1 在下列函数中,哪些是一次函数?请指出一次函数中的k 和b 的值.
(1) y=2-x, (2) (3) s=8+0.03t,
(4) (5) (6)
解:(1)(3)(4)(5)是一次函数.(1)中k=-1,b=2;(3)中的k=0.03,b=8;(4)中的k= ,b=0;
(5)中的k= ,b=-3.
典题精讲
在下列函数中,哪些是一次函数?请指出一次函数中的k 和b 的值.
解:(1)(2)(4)是一次函数.(1)中的k=-1,b= ;
(2)中的k=2π,b=0;(4)中的k=0.5,b= .
典题精讲
3 下列函数中,y 是x 的一次函数的是( )
A.y=x 2+2x B.y=-
C.y=x D.y= +1
下列函数:①y=2x-1;②y=πx;③y= ;
④y=x 2中,一次函数的个数是( )
A.1 B.2 C.3 D.4
C
B
典题精讲
5 已知y=(m-3)x |m |-2+1是y 关于x 的一次函数,则m的值是( )
A.-3 B.3 C.±3 D.±2
6 若3y-4与2x-5成正比例,则y 是x 的( )
A.正比例函数 B.一次函数
C.没有函数关系 D.以上均不正确
A
B
探索新知
例2 已知关于x 的函数y=(2m-1)x+1-3m,当m满足什么条件时,
(1)这个函数是正比例函数?
(2)这个函数为一次函数?
导引:根据正比例函数和一次函数的定义求解即可.
探索新知
解:(1)∵函数y=(2m-1)x+1-3m 是正比例函数,∴1-3m=0,2m-1≠0,∴m= .∴当m= 时,这个函数是正比例函数.
(2)∵函数y=(2m-1)x+1-3m 是一次函数,
∴2m-1≠0,解得m≠ .∴当m≠ 时,这个函数为一次函数.
探索新知
总 结
一次函数y=kx+b 中k、b 为常数,k≠0,自变量
的次数为1.当b=0时,一次函数y=kx+b 就化为正比
例函数y=kx.
典题精讲
1 已知一次函数y =-2x +3.
(1) 当x 为何值时,y=0?
(2) 当y 为何值时,x=0?
解: (1)对于一次函数y=-2x+3,令y=0,
即-2x+3=0,解得x= .所以当x= 时,y=0.
(2)将x=0代入y=-2x+3中,得y=-2×0+3=3.
所以当y=3时,x=0.
探索新知
2
知识点
确定应用问题中的一次函数表达式
当“条件”中明确是一次函数关系时,可利用关系式y=kx+b 求解,依据已知求得k、b 的值就可以了;当“条件”中未明确是一次函数关系时(一般情况是实际应用题),我们应依据已知中的基本数量列出等量关系(类似列方程解应用题),再整理成y=kx+b (k,b 为常数,k≠0)的形式.
注意:在列出有关实际问题的一次函数关系式时,应标注自变量的取值范围.
探索新知
例3 如图所示, △ABC 是边长为x 的等边三角形.
(1)求BC 边上的高h 与x 之间的函数关系式. h 是x 的一次函数吗?如果是一次函数,请指出相应的k 与b 的值.
(2) 当h= 时,求x 的值.
(3)求△ABC 的面积S 与x 之间的函数
关系式. S 是x 的一次函数吗?
探索新知
解:(1)因为BC 边上的高AD 也是BC 边上的中线,所以
BD= .在Rt△ABD 中,由勾股定理,得
即
所以h 是x 的一次函数,且 .
探索新知
(2)当 时,有 .
解得x =2.
(3)因为
即 所以S 不是x 的一次函数.
典题精讲
已知两条平行线l1,l2 之间的距离为3 cm,点A 在l1 上,点B,C 在l2 上,BC=x. 求△ABC 的面积S 与x的函数关系式,并判断这个函数是不是一次函数.
解: S= ·BC · 3= x,这个函数是一次函数.
典题精讲
2 一个正方形的边长为3 cm,它的各边边长均减少x cm后,得到的新正方形的周长为y cm,y 与x 之间的函数表达式是( )
A.y=12-4x B.y=4x-12
C.y=12-x D.以上都不对
A
学以致用
小试牛刀
1 下列说法正确的是( )
A.正比例函数是一次函数
B.一次函数是正比例函数
C.对于变量x 与y,y 是x 的函数,x 不是y 的函数
D.正比例函数不是一次函数,一次函数也不是正比例函数
A
2 如图,图像表示的一次函数表达式为( )
A.y=-x-5
B.y=x-5
C.y=x+5
D.y=-x+5
小试牛刀
D
小试牛刀
3
我们知道,海拔高度每上升1千米,温度下降6 ℃.某时刻,益阳地面温度为20 ℃,设高出地面x 千米处的温度为y ℃.
(1)写出y 与x 之间的函数关系式;
(2)已知益阳碧云峰高出地面约500米,求这时山顶的温度大约是多少?
(3)此刻,有一架飞机飞过益阳上空,若机舱内仪表显示飞机外面的温度为-34 ℃,求飞机离地面的高度为多少千米?
小试牛刀
(1)y=20-6x (x>0).
(2)500米=0.5千米,当x=0.5时,y=20-6×0.5=17.
即这时山顶的温度大约为17 ℃.
(3)当y=-34时,有-34=20-6x,解得x=9.
即飞机离地面的高度为9千米.
解:
小试牛刀
4
学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人,如图所示,请你结合这个规律,填写下表并回答问题:
(1)写出y 与x 之间的函数解析式,并判断y 是不是x 的一次函数;
(2)若八年级(1)班有42人去阅览室看书,则需要多少张这样的方桌拼成一行?
拼成一行的方桌数(x ) 1 2 3 4 …
人数(y ) 4 6 8 …
10
小试牛刀
(1)y=2x+2,y 是x 的一次函数.
(2)把y=42代入y=2x+2中,
得42=2x+2,
解得x=20.
答:需要20张这样的方桌拼成一行.
解:
课堂小结
课堂小结
正比例函数与一次函数的关系
正比例函数是一次函数的特例,一次函数包括正比
例函数,用图形表示它们之
间的关系如图所示:
一次函数y=kx+b (k≠0) ,当b=0时是特殊的一次函数(即正比例函数),当b ≠ 0时是一般的一次函数.
一次函数
正比例函数
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
