【班海精品】冀教版(新)八下-21.2 一次函数的图像和性质 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-21.2 一次函数的图像和性质 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览










文档简介
(共50张PPT)
21.2 一次函数的图像和性质
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,显示的是一个自行车骑车手骑车时热量
消耗W (焦)与身体质量x (千克)之间的关系,你能写出W
与x 之间的关系式吗?
新课精讲
探索新知
1
知识点
一次函数的性质
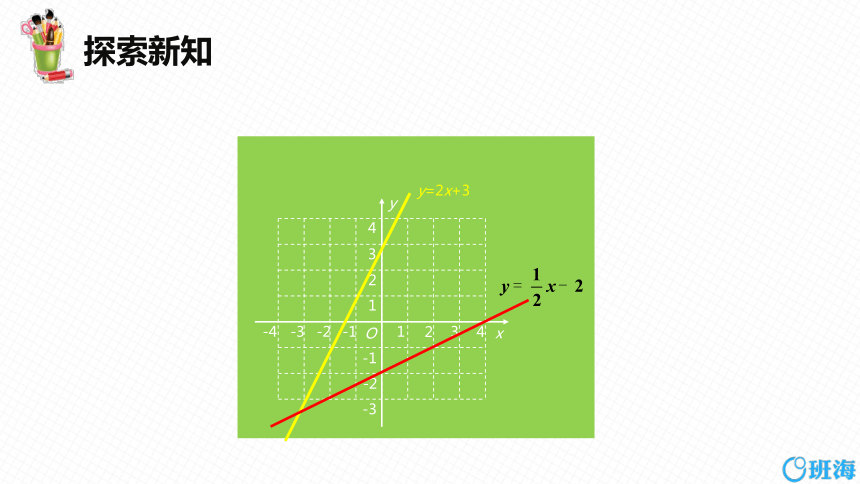
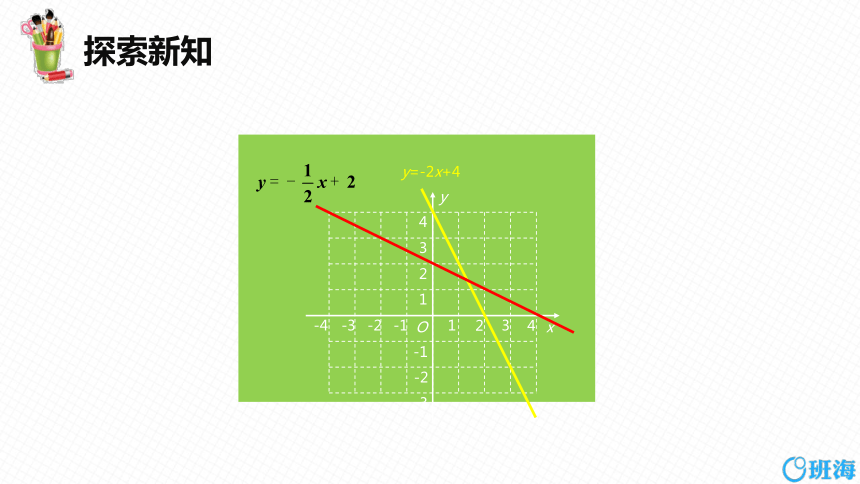
在下图所示的两个坐标系中,分别画出一次函数
y =2x+3、 y = x-2和y =-2x+4、y =- x+2
的图像,并回答以下问题:
探索新知
y
O
x
-1
-2
-3
-4
4
3
2
1
-1
-2
-3
4
3
2
1
y=2x+3
探索新知
y
O
x
-1
-2
-3
-4
4
3
2
1
-1
-2
-3
4
3
2
1
y=-2x+4
探索新知
哪些函数,y 的值是随x 的值的增大而增大的?
哪些函数,y 的值是随x 的值的增大而减小的?
y 的值随x 的增大而增大和y 的值随x 值的增大而减小两种
函数,它们的区别和自变量系数的符号有怎样的关系?
由图可知,y =2x+3和 两个函数y 的值是随x
的值的增大而增大的;y=-2x+4和 两个函数
y 的值是随x 的值的增大而减小的.而这两组函数的区别
在于:前两个函数的自变量系数是正的,而后两个函数
的自变量系数是负的.
探索新知
一般地,我们有:
对于一次函数y=kx+b(k,b 为常数,且k≠0):
当k >0时,y 的值随x 的值的增大而增大;
当k <0时,y 的值随x 的值的增大而减小.
探索新知
例1 已知一次函数y=(6+3m)x+(m-4),y 随x 的增大而增大,函数的图像与y 轴的交点在y 轴的负半轴上,求m 的取值范围.
导引:根据一次函数的性质可知,6+3m>0,且m-4<0,联立解不等式组即可.
解:根据题意,得 ,解得-2<m<4.
所以m 的取值范围是-2<m<4.
探索新知
总 结
对于一次函数y=kx+b (k≠0),(1)判断k 值符号的方法:①增减性法:当y 随x 的增大而增大时,k>0;反之,k<0.②直线升、降法:当直线从左到右上升时,k>0;反之,k<0.③经过象限法:当直线过第一、三象限时,k>0;当直线经过第二、四象限时,k<0.(2)判断b 值符号的方法:与y 轴交点法,即若直线y=kx+b 与y 轴交于正半轴,则b>0;与y 轴交于负半轴,则b<0;与y 轴交于原点,则b=0.
典题精讲
1 判断下列函数中,y 的值随x 的值增大而变化的情况.
(1) y =-3x+3; (2) y =3x-3;
(3) y =(3-π)x; (4)y =0.5x
(1)y 随x 的增大而减小.
(2)y 随x 的增大而增大.
(3)y 随x 的增大而减小.
(4)y 随x 的增大而增大.
解:
典题精讲
2 已知关于x 的一次函数y =kx+4k-2.
(1)如果函数的图像经过原点,求k 的值.
(2)如果 y 的值随x 的值增大而减小,求k 的取值范围.
(1)由题意得,k≠0,且4k-2=0,解得k= .
(2)由题意得,k<0.
解:
典题精讲
已知一次函数y =(k+1) x-1, y 的值随x 的值增大
而减小,求k 的取值范围.
解:由题意得,k+1<0,所以k<-1.
典题精讲
4 画出函数y=-3x+3的图像,结合图像回答下列问题.
(1) y 的值随x 的值增大而_____(填“增大”或“减小”),图像从左到右逐渐_______(填“上升”或“下降”)
(2)当y<0时,求x 的取值范围.
(2)当0 < x<1时,求y 的取值范围.
典题精讲
图像如图所示.
(1)减小;下降
(2)当y<0时,x>1.
(3)当0<x<1时,
0<y<3.
解:
典题精讲
5 已知P1(x1,y1),P2(x2,y2)是一次函数y=- x+2图像上的两点,下列判断中,正确的是( )
A.y1>y2
B.y1<y2
C.当x1<x2时,y1<y2
D.当x1<x2时,y1>y2
D
典题精讲
6 下列一次函数中,y 随x 的增大而减小的是( )
①y=-(2x-1);②y=- ;
③y=(2- )x+1;④y= (6-x).
A.①和② B.②和③
C.①和④ D.③和④
C
典题精讲
7 一次函数y= x+3的图像如图所示,当y>0时x 的取值范围是( )
A.x>2
B.x<2
C.x<0
D.2<x<4
B
典题精讲
8 下列函数中,同时满足下面两个条件的是( )
①y 随着x 的增大而增大;
②其图像与x 轴的正半轴相交.
A.y=-2x-1 B.y=-2x+1
C.y=2x-1 D.y=2x+1
D
典题精讲
9 已知点(-1,y1),(4,y2)在一次函数y=3x-2的图像
上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2
C.y1<y2<0 D.y2<0<y1
B
探索新知
2
知识点
一次函数性质的应用
参考上面画出的四个函数y=2x+3, y= x-2,
y=-2x+4,y=- x+2的图像,请谈谈:
(1)哪些函数的图像与y 轴的交点在x 轴的上方,哪些函
数与y 轴的交点在x 轴的下方?
(2)函数的图像与y 轴的交点在x 轴的上方和函数的图像
与y 轴的交点在x 轴的下方,这两种函数,它们的区
别与常数项有怎样的关系?
(3)正比例函数的图像一定经过哪个点?
探索新知
事实上,一次函数y=kx+b 的图像是经过y 轴上的
点(0,b)的一条直线.当b>0时,点(0,b)在x 轴的上方;
当b<0时,点(0,b)在x 轴的下方;当b=0时,点(0,0)
是原点,即正比例函数y=kx 的图像是经过原点的一条直线.
探索新知
例2 已知关于x的一次函数y=(2k-1) x+(2k+1).
(1) 当k 满足什么条件时,函数y 的值随x 的值增大而增大.
(2) 当k 取何时,y=(2k-1) x+(2k+1)的图像经过原点.
(3) 当k 满足什么条件时,函数y=(2k-1) x+(2k+1)的图像与y 轴的交点在x 轴的下方.
探索新知
(1)当2k-1>0时, y 的值随x 的值增大而增大.
解2k-1>0,得k> .
(2)当2k-1=0时,即k= 时,函数y=(2k-1) x+(2k+1)的图像经过原点.
(3)当2k-1<0时,函数y=(2k-1) x+(2k+1)的图像与y 轴的交点在x 轴的下方.
解2k-1< 0,得k< .
解:
典题精讲
1 在同一直角坐标系中,画出一次函数 ,
的图像,并回答:
(1)各图像的位置有什么关系?
(2)这种位置关系与函数表达式中的哪个量相关?
典题精讲
所画函数图像如图所示.
(1)三条直线平行.
(2)与函数表达式中
的k 相关.
解:
典题精讲
2 在同一直角坐标系中,画出函数①y=x+3,②y=x-3,③y=-x+3, ④y=-x-3的图像,并找出每两个函数图像之间的共同特征.
所画函数图像如图所示.
每两个函数图像之间的
共同特征略.
解:
典题精讲
3 某面食加工部每周用10 000元流动资金采购面粉及其他物品.其中购买面粉的质量在1 500 kg 2 000 kg之间,面粉的单价为3.6元/千克,用剩余款额y 元购买其他物品.设购买面粉的质量为x kg.
(1)求y 与x 的函数关系式,并写出自变量的取值范围.
(2)画出该函数的图像.
(3)观察图像,写出购买其他物品的款额y 的取值范围.
典题精讲
(1)y=10 000-3.6x (1 500≤ x ≤2 000).
(2)函数图像如图所示.
(3)2 800≤ y ≤4 600.
解:
典题精讲
4 若正比例函数y=kx (k≠0)的函数值y 随x 的增大而减小,则一次函数y=kx+k 的图像大致是( )
D
典题精讲
5 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD 的顶点都在格点上.若直线y=kx (k≠0)与正方形ABCD有公共点,则k 的取值范围是( )
A.k≤2 B.k≥
C. ≤k≤2 D.C
典题精讲
6 若一次函数y=mx+|m-1|的图像经过点(0,2),且y 随x 的增大而增大,则m 的值为______.
7 如图,一次函数y=(m-5)x+6-2m 的图像分别与x 轴、y 轴交于A,B 两点,则m 的取值范围是 .
3
3典题精讲
8 已知一次函数y=kx+2k+3的图像与y 轴的交点在y 轴的正半轴上,且函数值y 随x 的增大而减小,则k 所能取到的整数值为________.
-1
易错提醒
已知一次函数y=kx+b,当-3≤ x ≤1时,对应的y 值为-1≤ y ≤ 8,则b 的值是( )
A. B.
C. D.
易错点:对函数性质理解不透彻导致漏解.
C
学以致用
小试牛刀
1 若点M (-7,m ),N (-8,n )都在函数y=-(k 2+2k+4)x+1(k 为常数)的图像上,则m 和n 的大小关系是( )
A.m>n B.m<n
C.m=n D.不能确定
B
小试牛刀
2
已知一次函数y=(m+3)x+m 2-16,且y 的值
随x 值的增大而增大.
(1)求m 的取值范围;
(2)若此一次函数又是正比例函数,求m 的值.
小试牛刀
(1)由题意得m+3>0,
解得m>-3.
(2)由题意得m 2-16=0,解得m=±4,
又因为m>-3,
所以m=4.
解:
小试牛刀
3
已知一次函数y=(6+3m)x+(n-4).
(1)当m 为何值时,y 随x 的增大而减小?
(2)当m,n 为何值时,函数的图像与y 轴的交
点在x 轴的下方?
(3)当m,n 为何值时,函数的图像经过原点?
小试牛刀
解:
(1)因为y 随x 的增大而减小,
所以6+3m<0,解得m<-2.
(2)由题意得6+3m≠0,n-4<0,
解得m≠-2,n<4.
(3)由题意得6+3m≠0,n-4=0,
解得m≠-2,n=4.
小试牛刀
4
如图,已知直线y=2x+4与x 轴交于点A,与y 轴交于点B,直线AB上有一点Q 在第一象限且到y 轴的距离为2.
(1)求点A、B、Q 的坐标;
(2)若点P 在x 轴上,且PO=24,
求△APQ 的面积.
小试牛刀
(1)∵直线y=2x+4与x 轴交于点A,与y 轴交于点B,
且当y=0时,x=-2,
当x=0时,y=4,∴A (-2,0),B (0,4).
∵点Q 在直线AB上,又在第一象限且到y 轴的距离为2,
∴点Q 的横坐标为2,此时y=4+4=8,
∴Q (2,8).
解:
小试牛刀
(2)由A (-2,0)得OA=2,
由Q (2,8)可得△APQ 中AP 边上的高为8,
当点P 在x 轴的正半轴上时,
AP=OA+PO=2+24=26,
S△APQ= ×26×8=104;
当点P′ 在x 轴的负半轴上时,
AP′=P′O-OA=24-2=22,
S△AP′Q= ×22×8=88.
综上所述,△APQ 的面积为104或88.
小试牛刀
5
一次函数的解析式为y=ax-a+1(a 为常数,且a≠0).
(1)若点 在一次函数y=ax-a+1的图象上,
求a 的值;
(2)当-1≤x≤2时,函数有最大值2,请求出a 的值.
小试牛刀
(1)将点 的坐标代入y=ax-a+1中,得
3=- a-a+1,解得a=- .
(2)当x=-1时,y=-2a+1,当x=2时,y=a+1.
当-2a+10时,
a+1=2,则a=1,符合条件.
当-2a+1>a+1,即a<0时,-2a+1=2,
则a=- ,符合条件,所以a=1或a=- .
解:
课堂小结
课堂小结
1. 一次函数y=kx+b 的图像为一条直线,故其图像又称为直线y=kx+b.
2. 一次函数y=kx+b 中的系数k 与b 决定着它的性质:
(1)当k>0时,y 随x 的增大而增大,图像从左向右是上升的.
(2)当k<0时,y 随x 的增大而减小,图像从左向右是下降的.
(3)当b=0时,一次函数y=kx+b 为正比例函数y=kx,它的图像一定经过原点.
(4)当b≠0时,直线y=kx+b 一定不经过原点.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
21.2 一次函数的图像和性质
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,显示的是一个自行车骑车手骑车时热量
消耗W (焦)与身体质量x (千克)之间的关系,你能写出W
与x 之间的关系式吗?
新课精讲
探索新知
1
知识点
一次函数的性质
在下图所示的两个坐标系中,分别画出一次函数
y =2x+3、 y = x-2和y =-2x+4、y =- x+2
的图像,并回答以下问题:
探索新知
y
O
x
-1
-2
-3
-4
4
3
2
1
-1
-2
-3
4
3
2
1
y=2x+3
探索新知
y
O
x
-1
-2
-3
-4
4
3
2
1
-1
-2
-3
4
3
2
1
y=-2x+4
探索新知
哪些函数,y 的值是随x 的值的增大而增大的?
哪些函数,y 的值是随x 的值的增大而减小的?
y 的值随x 的增大而增大和y 的值随x 值的增大而减小两种
函数,它们的区别和自变量系数的符号有怎样的关系?
由图可知,y =2x+3和 两个函数y 的值是随x
的值的增大而增大的;y=-2x+4和 两个函数
y 的值是随x 的值的增大而减小的.而这两组函数的区别
在于:前两个函数的自变量系数是正的,而后两个函数
的自变量系数是负的.
探索新知
一般地,我们有:
对于一次函数y=kx+b(k,b 为常数,且k≠0):
当k >0时,y 的值随x 的值的增大而增大;
当k <0时,y 的值随x 的值的增大而减小.
探索新知
例1 已知一次函数y=(6+3m)x+(m-4),y 随x 的增大而增大,函数的图像与y 轴的交点在y 轴的负半轴上,求m 的取值范围.
导引:根据一次函数的性质可知,6+3m>0,且m-4<0,联立解不等式组即可.
解:根据题意,得 ,解得-2<m<4.
所以m 的取值范围是-2<m<4.
探索新知
总 结
对于一次函数y=kx+b (k≠0),(1)判断k 值符号的方法:①增减性法:当y 随x 的增大而增大时,k>0;反之,k<0.②直线升、降法:当直线从左到右上升时,k>0;反之,k<0.③经过象限法:当直线过第一、三象限时,k>0;当直线经过第二、四象限时,k<0.(2)判断b 值符号的方法:与y 轴交点法,即若直线y=kx+b 与y 轴交于正半轴,则b>0;与y 轴交于负半轴,则b<0;与y 轴交于原点,则b=0.
典题精讲
1 判断下列函数中,y 的值随x 的值增大而变化的情况.
(1) y =-3x+3; (2) y =3x-3;
(3) y =(3-π)x; (4)y =0.5x
(1)y 随x 的增大而减小.
(2)y 随x 的增大而增大.
(3)y 随x 的增大而减小.
(4)y 随x 的增大而增大.
解:
典题精讲
2 已知关于x 的一次函数y =kx+4k-2.
(1)如果函数的图像经过原点,求k 的值.
(2)如果 y 的值随x 的值增大而减小,求k 的取值范围.
(1)由题意得,k≠0,且4k-2=0,解得k= .
(2)由题意得,k<0.
解:
典题精讲
已知一次函数y =(k+1) x-1, y 的值随x 的值增大
而减小,求k 的取值范围.
解:由题意得,k+1<0,所以k<-1.
典题精讲
4 画出函数y=-3x+3的图像,结合图像回答下列问题.
(1) y 的值随x 的值增大而_____(填“增大”或“减小”),图像从左到右逐渐_______(填“上升”或“下降”)
(2)当y<0时,求x 的取值范围.
(2)当0 < x<1时,求y 的取值范围.
典题精讲
图像如图所示.
(1)减小;下降
(2)当y<0时,x>1.
(3)当0<x<1时,
0<y<3.
解:
典题精讲
5 已知P1(x1,y1),P2(x2,y2)是一次函数y=- x+2图像上的两点,下列判断中,正确的是( )
A.y1>y2
B.y1<y2
C.当x1<x2时,y1<y2
D.当x1<x2时,y1>y2
D
典题精讲
6 下列一次函数中,y 随x 的增大而减小的是( )
①y=-(2x-1);②y=- ;
③y=(2- )x+1;④y= (6-x).
A.①和② B.②和③
C.①和④ D.③和④
C
典题精讲
7 一次函数y= x+3的图像如图所示,当y>0时x 的取值范围是( )
A.x>2
B.x<2
C.x<0
D.2<x<4
B
典题精讲
8 下列函数中,同时满足下面两个条件的是( )
①y 随着x 的增大而增大;
②其图像与x 轴的正半轴相交.
A.y=-2x-1 B.y=-2x+1
C.y=2x-1 D.y=2x+1
D
典题精讲
9 已知点(-1,y1),(4,y2)在一次函数y=3x-2的图像
上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2
C.y1<y2<0 D.y2<0<y1
B
探索新知
2
知识点
一次函数性质的应用
参考上面画出的四个函数y=2x+3, y= x-2,
y=-2x+4,y=- x+2的图像,请谈谈:
(1)哪些函数的图像与y 轴的交点在x 轴的上方,哪些函
数与y 轴的交点在x 轴的下方?
(2)函数的图像与y 轴的交点在x 轴的上方和函数的图像
与y 轴的交点在x 轴的下方,这两种函数,它们的区
别与常数项有怎样的关系?
(3)正比例函数的图像一定经过哪个点?
探索新知
事实上,一次函数y=kx+b 的图像是经过y 轴上的
点(0,b)的一条直线.当b>0时,点(0,b)在x 轴的上方;
当b<0时,点(0,b)在x 轴的下方;当b=0时,点(0,0)
是原点,即正比例函数y=kx 的图像是经过原点的一条直线.
探索新知
例2 已知关于x的一次函数y=(2k-1) x+(2k+1).
(1) 当k 满足什么条件时,函数y 的值随x 的值增大而增大.
(2) 当k 取何时,y=(2k-1) x+(2k+1)的图像经过原点.
(3) 当k 满足什么条件时,函数y=(2k-1) x+(2k+1)的图像与y 轴的交点在x 轴的下方.
探索新知
(1)当2k-1>0时, y 的值随x 的值增大而增大.
解2k-1>0,得k> .
(2)当2k-1=0时,即k= 时,函数y=(2k-1) x+(2k+1)的图像经过原点.
(3)当2k-1<0时,函数y=(2k-1) x+(2k+1)的图像与y 轴的交点在x 轴的下方.
解2k-1< 0,得k< .
解:
典题精讲
1 在同一直角坐标系中,画出一次函数 ,
的图像,并回答:
(1)各图像的位置有什么关系?
(2)这种位置关系与函数表达式中的哪个量相关?
典题精讲
所画函数图像如图所示.
(1)三条直线平行.
(2)与函数表达式中
的k 相关.
解:
典题精讲
2 在同一直角坐标系中,画出函数①y=x+3,②y=x-3,③y=-x+3, ④y=-x-3的图像,并找出每两个函数图像之间的共同特征.
所画函数图像如图所示.
每两个函数图像之间的
共同特征略.
解:
典题精讲
3 某面食加工部每周用10 000元流动资金采购面粉及其他物品.其中购买面粉的质量在1 500 kg 2 000 kg之间,面粉的单价为3.6元/千克,用剩余款额y 元购买其他物品.设购买面粉的质量为x kg.
(1)求y 与x 的函数关系式,并写出自变量的取值范围.
(2)画出该函数的图像.
(3)观察图像,写出购买其他物品的款额y 的取值范围.
典题精讲
(1)y=10 000-3.6x (1 500≤ x ≤2 000).
(2)函数图像如图所示.
(3)2 800≤ y ≤4 600.
解:
典题精讲
4 若正比例函数y=kx (k≠0)的函数值y 随x 的增大而减小,则一次函数y=kx+k 的图像大致是( )
D
典题精讲
5 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD 的顶点都在格点上.若直线y=kx (k≠0)与正方形ABCD有公共点,则k 的取值范围是( )
A.k≤2 B.k≥
C. ≤k≤2 D.
典题精讲
6 若一次函数y=mx+|m-1|的图像经过点(0,2),且y 随x 的增大而增大,则m 的值为______.
7 如图,一次函数y=(m-5)x+6-2m 的图像分别与x 轴、y 轴交于A,B 两点,则m 的取值范围是 .
3
3
8 已知一次函数y=kx+2k+3的图像与y 轴的交点在y 轴的正半轴上,且函数值y 随x 的增大而减小,则k 所能取到的整数值为________.
-1
易错提醒
已知一次函数y=kx+b,当-3≤ x ≤1时,对应的y 值为-1≤ y ≤ 8,则b 的值是( )
A. B.
C. D.
易错点:对函数性质理解不透彻导致漏解.
C
学以致用
小试牛刀
1 若点M (-7,m ),N (-8,n )都在函数y=-(k 2+2k+4)x+1(k 为常数)的图像上,则m 和n 的大小关系是( )
A.m>n B.m<n
C.m=n D.不能确定
B
小试牛刀
2
已知一次函数y=(m+3)x+m 2-16,且y 的值
随x 值的增大而增大.
(1)求m 的取值范围;
(2)若此一次函数又是正比例函数,求m 的值.
小试牛刀
(1)由题意得m+3>0,
解得m>-3.
(2)由题意得m 2-16=0,解得m=±4,
又因为m>-3,
所以m=4.
解:
小试牛刀
3
已知一次函数y=(6+3m)x+(n-4).
(1)当m 为何值时,y 随x 的增大而减小?
(2)当m,n 为何值时,函数的图像与y 轴的交
点在x 轴的下方?
(3)当m,n 为何值时,函数的图像经过原点?
小试牛刀
解:
(1)因为y 随x 的增大而减小,
所以6+3m<0,解得m<-2.
(2)由题意得6+3m≠0,n-4<0,
解得m≠-2,n<4.
(3)由题意得6+3m≠0,n-4=0,
解得m≠-2,n=4.
小试牛刀
4
如图,已知直线y=2x+4与x 轴交于点A,与y 轴交于点B,直线AB上有一点Q 在第一象限且到y 轴的距离为2.
(1)求点A、B、Q 的坐标;
(2)若点P 在x 轴上,且PO=24,
求△APQ 的面积.
小试牛刀
(1)∵直线y=2x+4与x 轴交于点A,与y 轴交于点B,
且当y=0时,x=-2,
当x=0时,y=4,∴A (-2,0),B (0,4).
∵点Q 在直线AB上,又在第一象限且到y 轴的距离为2,
∴点Q 的横坐标为2,此时y=4+4=8,
∴Q (2,8).
解:
小试牛刀
(2)由A (-2,0)得OA=2,
由Q (2,8)可得△APQ 中AP 边上的高为8,
当点P 在x 轴的正半轴上时,
AP=OA+PO=2+24=26,
S△APQ= ×26×8=104;
当点P′ 在x 轴的负半轴上时,
AP′=P′O-OA=24-2=22,
S△AP′Q= ×22×8=88.
综上所述,△APQ 的面积为104或88.
小试牛刀
5
一次函数的解析式为y=ax-a+1(a 为常数,且a≠0).
(1)若点 在一次函数y=ax-a+1的图象上,
求a 的值;
(2)当-1≤x≤2时,函数有最大值2,请求出a 的值.
小试牛刀
(1)将点 的坐标代入y=ax-a+1中,得
3=- a-a+1,解得a=- .
(2)当x=-1时,y=-2a+1,当x=2时,y=a+1.
当-2a+1
a+1=2,则a=1,符合条件.
当-2a+1>a+1,即a<0时,-2a+1=2,
则a=- ,符合条件,所以a=1或a=- .
解:
课堂小结
课堂小结
1. 一次函数y=kx+b 的图像为一条直线,故其图像又称为直线y=kx+b.
2. 一次函数y=kx+b 中的系数k 与b 决定着它的性质:
(1)当k>0时,y 随x 的增大而增大,图像从左向右是上升的.
(2)当k<0时,y 随x 的增大而减小,图像从左向右是下降的.
(3)当b=0时,一次函数y=kx+b 为正比例函数y=kx,它的图像一定经过原点.
(4)当b≠0时,直线y=kx+b 一定不经过原点.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
