【班海精品】冀教版(新)八下-21.3 用待定系数法确定一次函数表达式【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-21.3 用待定系数法确定一次函数表达式【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览











文档简介
(共48张PPT)
21.3 用待定系数法确定一次函数表达式
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
通过直接列式可以求一次函数表达式. 当然,还
有其他的方法求一次函数表达式. 本节将探究用待定
系数的方法来求一次函数的表达式.
新课精讲
探索新知
1
知识点
用待定系数法求正比例函数表达式
由于正比例函数的解析式y=kx (k≠0)中,只有一个基本量k (我们也称待定系数),因此只需要一个条件就可以求得k的值,从而确定正比例函数的解析式.
比如已知满足函数解析式y=kx 的一组x,y 的值或已知直线y=kx 上的一个点等都可以确定正比例函数的解析式.
探索新知
注意:先假定解析式中的未知系数,然后根据已知
条件求出待定的系数,从而确定出该解析式的方法
是数学上常用的方法,这种方法称为待定系数法.
探索新知
例1 y 与x+2成正比例,并且当x =4时,y =10,求y与x 的函数关系式.
导引:根据正比例函数的定义,可以设y =k (x+2),然
后把x =4,y =10代入求出k 的值即可.
解:设y =k (x+2),∵x =4时,y =10,
∴10=k (4+2),解得k = ,
∴y = (x+2)
探索新知
总 结
熟记正比例函数的定义,必须满足自变量x 的次数为1,系数k 不为0.
典题精讲
1 求函数的表达式:正比例函数的图像经过点(2,-1).
设正比例函数的表达式为y=kx,将点(2,-1)的坐标代入,可得2k=-1,解得k=- .所以正比例函数的表达式为y=- x.
解:
典题精讲
2 已知正比例函数y=kx (k≠0)的图像经过点(1,-2),则这个正比例函数的表达式为( )
A.y=2x B.y=-2x
C.y= x D.y=- x
B
探索新知
2
知识点
用待定系数法求一次函数表达式
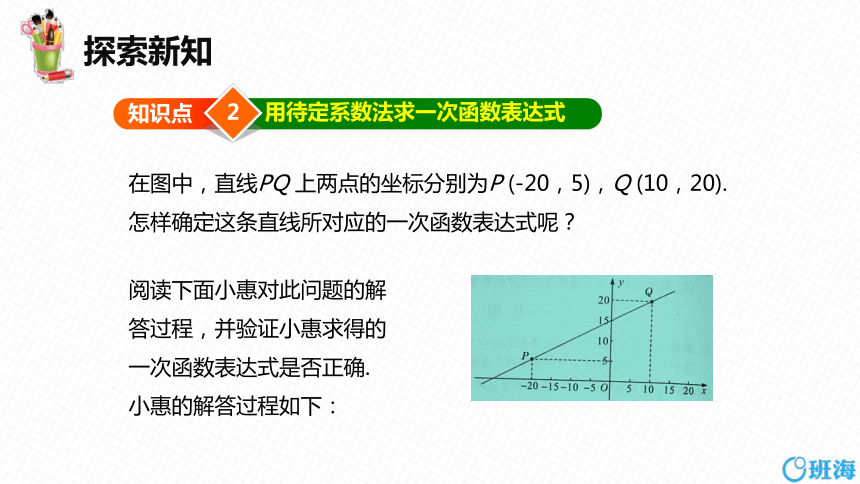
在图中,直线PQ 上两点的坐标分别为P (-20,5),Q (10,20).怎样确定这条直线所对应的一次函数表达式呢?
阅读下面小惠对此问题的解
答过程,并验证小惠求得的
一次函数表达式是否正确.
小惠的解答过程如下:
探索新知
设这个一次函数表达式为y=kx+b.
因为P,Q 为直线上的两点,所以这两个点的坐标都满
足表达式y=kx+b ,即
解这个关于k 和b 的二元一次方程组,得
所以,这个一次函数表达式为
探索新知
像这样先设出函数表达式,再根据已知条件确定表达
式中未知的系数,从而求出函数表达式的方法,叫做
待定系数法.
探索新知
例2 一辆汽车匀速行驶,当行驶了 20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油y (L)与汽车行驶的路程x (km)之间是一次函数关系,请求出这个一次函数的表达式, 并写出自变量x 的取值范围以及常数项的意义.
探索新知
设所求一次函数的表达式为y=kx+b. 根据题意,
把已知的两组对应值(20,58. 4)和(50,56)代入
y=kx+b,得
解得
这个一次函数表达式为y=-0.08x+60.
因为剩余油量y ≥0,所以-0.08x+60 ≥0.解得x ≤750.
因为路程x ≥0,所以0≤ x ≤750.
因为当x =0时,y =60,所以这辆汽车行驶前油箱存油60 L.
解:
探索新知
总 结
求一次函数的表达式一般要经过设、列、解、还
原四步,设就是设出一次函数的表达式;列就是把已
知两点的坐标代入所设表达式,列出一个二元一次方
程组;解就是解这个方程组;还原就是回代所设表达
式得到所求的表达式.
典题精讲
1 某市举办一场中学生羽毛球比赛.场地和耗材需要一些费用.场地费b (元)是固定不变的.耗材费用与参赛人数x (人)成正比例函数关系.这两部分的总费用为y (元).已知当x =20时,y =1 600;当x =30时,y =2 000.
(1)求y 与x 之间的函数关系式.
(2)当支出总费用为3 200元时,有多少人参加了比赛?
典题精讲
(1)设y 与x 之间的函数关系式为y=kx+b,因为当x=20时,y=1 600;当x=30时,y=2 000,
所以 解得
所以y=40x+800(x 为正整数).
(2)当y=3 200时,40x+800=3 200,解得x=60.所以当支出总费用为3 200元时,有60人参加了比赛.
解:
典题精讲
2 为保护学生的视力,供学生使用的课桌和椅子的高度均需按一定的关系配套设计.研究表明:课桌高度y (cm)与椅子高度x (cm)具有一次函数关系.今有两套符合条件的课桌和椅子,其高度如下表所示:
(1)试确定y 与x 的函数关系式.
(2)现有一把高为42.0cm的椅子和一张高为78.2cm的课桌,它们是否配套?为什么?
项目 第一套 第二套
x /cm 40.0 37.0
y /cm 75.0 70.2
典题精讲
(1)设y 与x 的函数关系式为y=kx+b,将(40.0,75.0)和(37.0,70.2)分别代入,
得 解得
所以y=1.6x+11.
(2)配套.理由:当x=42.0时,y=1.6×42.0+11=78.2,所以它们配套.
解:
典题精讲
3 若一次函数y=kx+b 的图像经过点(0,2)和(1,0),则这个函数的表达式是( )
A.y=2x+3 B.y=3x+2
C.y=x+2 D.y=-2x+2
D
4 根据表中一次函数的自变量x 与函数y 的对应值,可得p 的值为( )
A.1 B.-1 C.3 D.-3
A
x -2 0 1
y 3 p 0
典题精讲
5 若点A (m,n)在一次函数y=3x+b 的图像上,且3m-n>2,则b 的取值范围为( )
A.b>2 B.b>-2
C.b<2 D.b<-2
D
6 一次函数y=-2x+m 的图像经过点P (-2,3),且与x 轴,y 轴分别交于点A,B,则△AOB 的面积是( )
A. B.
C.4 D.8
B
探索新知
3
知识点
用关系式法求一次函数表达式
例3 已知一次函数y=kx+b,当x=0时,y=1;当x=1时,y=0.试确定这个函数的表达式.
分别将x=0,y=1和x=1,y=0代入y=kx+b 中,
得到关于k、b 的二元一次方程组,解之即可.
将x=0,y=1和x=1,y=0分别代入y=kx+b,
得 解得
所以这个函数的表达式为y=-x+1.
导引:
解:
探索新知
总 结
满足一次函数表达式的一对对应值就是将一次函
数表达式作为方程时的一组解.将函数问题转化为方
程问题来解决.
典题精讲
1 一次函数的图像经过点A (1,2)和点B (-2,1),求这个函数的表达式.
设此一次函数的表达式为y=kx+b,把点(1,2),(-2,1)的坐标分别代入
得 解得
故这个函数的表达式为y=
解:
典题精讲
2 如果一次函数y =(k+3)x-13的图像上一点P 的坐标为(-5, 7),那么k 的值为_________.
3 一次函数的图像经过点(-1,-2)和( , 3).求函数的表达式.
-7
设一次函数的表达式为y=kx+b,将点(-1,-2),( , 3)的坐标分别代入,
可得 解得
所以此一次函数的表达式为y=
解:
典题精讲
4 已知一次函数的图像如图所示,求这个函数的表达式.
设这个函数的表达式为y=kx+b,
将点(0,2),(3,-4)的坐标分别
代入,
可得 解得
所以这个函数的表达式为y=-2x+2.
解:
典题精讲
5 已知y 是x 的一次函数,当x=3时,y=1;当x=-2时,y=-4.求这个一次函数的表达式.
设这个一次函数的表达式为y=kx+b (k≠0),将x=3,y=1和x=-2,y=-4分别代入上式得
可得 解得
所以这个函数的表达式为y=x-2.
解:
典题精讲
6 已知y+2与x-1成正比例,且当x=3时,y=4.
(1)求y 与x 之间的函数表达式;
(2)当y=1时,求x 的值.
(1)设y+2=k (x-1)(k≠0),把x=3,y=4代入,得4+2=k (3-1),解得k=3.
则y 与x 之间的函数表达式是y+2=3(x-1),
即y=3x-5.
(2)当y=1时,3x-5=1,解得x=2.
解:
典题精讲
7 根据下列条件,分别确定y 关于x 的函数表达式.
(1)y 与x 成正比例,且当x=9时,y=16;
(2)已知一次函数y=kx+b,当x=3时,y=2;当x=-2时,y=1.
(1)设y=k ′x (k ′≠0),把x=9,y=16代入,得16=9k ′,k ′= ,所以y= x.
解:
典题精讲
(2)把x=3,y=2和x=-2,y=1分别代入y=kx+b,
得 解得
所以y=
易错提醒
已知函数y=(n+3)x |n |-2是一次函数,则n=_______.
易错点:忽略一次函数中的k≠0这一条件导致错误.
3
学以致用
小试牛刀
1 若一个正比例函数的图像经过A (3,-6),B (m,-4)
两点,则m 的值为( )
A.2 B.8
C.-2 D.-8
A
小试牛刀
2 如图,直线y= x+4与x 轴,y 轴分别交于点A 和点B,点C,D 分别是线段AB,OB 的中点,点P 为OA上一动点,当PC+PD最小时,点P 的坐标为( )
A.(-3,0)
B.(-6,0)
C.
D.
C
小试牛刀
3
在平面直角坐标系中,一次函数y=kx+b (k,b 都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当-2<x ≤3时,求y 的取值范围;
(2)已知点P (m,n)在该函数的图象上,且m-n=4,求点P 的坐标.
小试牛刀
将(1,0),(0,2)代入y=kx+b
得: 解得:
∴这个函数的表达式为:y=-2x+2.
(1)把x=-2代入y=-2x+2得,y=6,
把x=3代入y=-2x+2得,y=-4,
∴y 的取值范围是-4≤ y<6.
(2)∵点P (m,n )在该函数的图象上,∴n=-2m+2.
∵m-n=4,∴m-(-2m+2)=4,
解得m=2. ∴n=-2,∴点P 的坐标为(2,-2).
解:
小试牛刀
4
如图,直线y= x+ 与两坐标轴分别交于A,B 两点.
(1)求∠ABO 的度数;
(2)过A 的直线l 交x 轴正半轴于C,AB=AC,求直线 l 对应的函数表达式.
小试牛刀
(1)对于直线y= x+ ,
令x=0,则y= ,
令y=0,则x=-1,
故点A 的坐标为(0, ),点B 的坐标为(-1,0),
则AO= ,BO=1,
∴AB= =2. ∴BO= AB,
∴∠BAO=30°. ∴∠ABO=60°.
解:
小试牛刀
(2)在△ABC 中,
∵AB=AC,AO⊥BC,
∴BO=CO,
则C 点的坐标为(1,0),
设直线l 对应的函数表达式为:y=kx+b (k,b为常数),
则 解得:
即直线 l 对应的函数表达式为:y=- x+ .
小试牛刀
5
小明受“乌鸦喝水”故事的启发,利用量桶和体积相同
的小球进行了如下操作:
请根据图中给出的信息,解答下列问题.
(1)放入一个小球,量桶中水面升高________cm;
(2)求放入小球后量桶中水面的高度y (cm)关于小球个
数x (个)的一次函数表达式(水未溢出,不要求写出
自变量的取值范围);
(3)量桶中至少放入几个小球时有水溢出?
2
小试牛刀
(2)设一次函数表达式为y=kx+b (k≠0).
把x=0,y=30及x=3,y=36分别代入函数解析
式,得 解得
即y=2x+30.
(3)由题意得2x+30>49,解得x>9.5.
因为x 是正整数,所以量桶中至少放入10个小球
时有水溢出.
解:
小试牛刀
6
小明对学校所添置的一批课桌、凳子进行观察后,发现它们可以根据人的身高来调节高度.于是,他测量了一套课桌、凳子相对应的四档高度,得到如下数据:
(1)小明经过对数据的探究发现:桌高y 是凳高x 的一次函数,请你求出这个函数的表达式(不要求写出x 的取值范围);
(2)小明回家后,测量了家里的写字台和凳子.写字台的高度为77 cm,凳子的高度为43.5 cm,请你判断它们是否配套,并说明理由.
档次 高度 第一档 第二档 第三档 第四档
凳高x (cm) 37.0 40.0 42.0 45.0
桌高y (cm) 70.0 74.8 78.0 82.8
小试牛刀
(1)设所求一次函数的表达式为y=kx+b (k,b 为常数,k≠0),任取表中的两组数据,不妨取(37.0,70.0)和(42.0,78.0)分别代入,
得 解得
∴所求一次函数的表达式为y=1.6x+10.8.
(2)不配套.理由:当x=43.5时,
y=1.6×43.5+10.8=80.4.
∵77≠80.4,∴不配套.
解:
课堂小结
课堂小结
用待定系数法求一次函数表达式要明确两点:
(1)具备条件:一次函数y=kx+b 中有两个不确定的系数k,b,需要两个独立的条件确定两个关于k,b 的方程,联立方程,解方程组求得k,b 的值.这两个条件通常是两个点的坐标或两对x,y 的值.
(2)确定方法:将两对已知变量的对应值分别代入y=kx+b 中,建立关于k,b 的方程组,通过解这个方程组,求出k,b,从而确定其表达式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
21.3 用待定系数法确定一次函数表达式
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
通过直接列式可以求一次函数表达式. 当然,还
有其他的方法求一次函数表达式. 本节将探究用待定
系数的方法来求一次函数的表达式.
新课精讲
探索新知
1
知识点
用待定系数法求正比例函数表达式
由于正比例函数的解析式y=kx (k≠0)中,只有一个基本量k (我们也称待定系数),因此只需要一个条件就可以求得k的值,从而确定正比例函数的解析式.
比如已知满足函数解析式y=kx 的一组x,y 的值或已知直线y=kx 上的一个点等都可以确定正比例函数的解析式.
探索新知
注意:先假定解析式中的未知系数,然后根据已知
条件求出待定的系数,从而确定出该解析式的方法
是数学上常用的方法,这种方法称为待定系数法.
探索新知
例1 y 与x+2成正比例,并且当x =4时,y =10,求y与x 的函数关系式.
导引:根据正比例函数的定义,可以设y =k (x+2),然
后把x =4,y =10代入求出k 的值即可.
解:设y =k (x+2),∵x =4时,y =10,
∴10=k (4+2),解得k = ,
∴y = (x+2)
探索新知
总 结
熟记正比例函数的定义,必须满足自变量x 的次数为1,系数k 不为0.
典题精讲
1 求函数的表达式:正比例函数的图像经过点(2,-1).
设正比例函数的表达式为y=kx,将点(2,-1)的坐标代入,可得2k=-1,解得k=- .所以正比例函数的表达式为y=- x.
解:
典题精讲
2 已知正比例函数y=kx (k≠0)的图像经过点(1,-2),则这个正比例函数的表达式为( )
A.y=2x B.y=-2x
C.y= x D.y=- x
B
探索新知
2
知识点
用待定系数法求一次函数表达式
在图中,直线PQ 上两点的坐标分别为P (-20,5),Q (10,20).怎样确定这条直线所对应的一次函数表达式呢?
阅读下面小惠对此问题的解
答过程,并验证小惠求得的
一次函数表达式是否正确.
小惠的解答过程如下:
探索新知
设这个一次函数表达式为y=kx+b.
因为P,Q 为直线上的两点,所以这两个点的坐标都满
足表达式y=kx+b ,即
解这个关于k 和b 的二元一次方程组,得
所以,这个一次函数表达式为
探索新知
像这样先设出函数表达式,再根据已知条件确定表达
式中未知的系数,从而求出函数表达式的方法,叫做
待定系数法.
探索新知
例2 一辆汽车匀速行驶,当行驶了 20 km时,油箱剩余58.4 L油;当行驶了50 km时,油箱剩余56 L油.如果油箱中剩余油y (L)与汽车行驶的路程x (km)之间是一次函数关系,请求出这个一次函数的表达式, 并写出自变量x 的取值范围以及常数项的意义.
探索新知
设所求一次函数的表达式为y=kx+b. 根据题意,
把已知的两组对应值(20,58. 4)和(50,56)代入
y=kx+b,得
解得
这个一次函数表达式为y=-0.08x+60.
因为剩余油量y ≥0,所以-0.08x+60 ≥0.解得x ≤750.
因为路程x ≥0,所以0≤ x ≤750.
因为当x =0时,y =60,所以这辆汽车行驶前油箱存油60 L.
解:
探索新知
总 结
求一次函数的表达式一般要经过设、列、解、还
原四步,设就是设出一次函数的表达式;列就是把已
知两点的坐标代入所设表达式,列出一个二元一次方
程组;解就是解这个方程组;还原就是回代所设表达
式得到所求的表达式.
典题精讲
1 某市举办一场中学生羽毛球比赛.场地和耗材需要一些费用.场地费b (元)是固定不变的.耗材费用与参赛人数x (人)成正比例函数关系.这两部分的总费用为y (元).已知当x =20时,y =1 600;当x =30时,y =2 000.
(1)求y 与x 之间的函数关系式.
(2)当支出总费用为3 200元时,有多少人参加了比赛?
典题精讲
(1)设y 与x 之间的函数关系式为y=kx+b,因为当x=20时,y=1 600;当x=30时,y=2 000,
所以 解得
所以y=40x+800(x 为正整数).
(2)当y=3 200时,40x+800=3 200,解得x=60.所以当支出总费用为3 200元时,有60人参加了比赛.
解:
典题精讲
2 为保护学生的视力,供学生使用的课桌和椅子的高度均需按一定的关系配套设计.研究表明:课桌高度y (cm)与椅子高度x (cm)具有一次函数关系.今有两套符合条件的课桌和椅子,其高度如下表所示:
(1)试确定y 与x 的函数关系式.
(2)现有一把高为42.0cm的椅子和一张高为78.2cm的课桌,它们是否配套?为什么?
项目 第一套 第二套
x /cm 40.0 37.0
y /cm 75.0 70.2
典题精讲
(1)设y 与x 的函数关系式为y=kx+b,将(40.0,75.0)和(37.0,70.2)分别代入,
得 解得
所以y=1.6x+11.
(2)配套.理由:当x=42.0时,y=1.6×42.0+11=78.2,所以它们配套.
解:
典题精讲
3 若一次函数y=kx+b 的图像经过点(0,2)和(1,0),则这个函数的表达式是( )
A.y=2x+3 B.y=3x+2
C.y=x+2 D.y=-2x+2
D
4 根据表中一次函数的自变量x 与函数y 的对应值,可得p 的值为( )
A.1 B.-1 C.3 D.-3
A
x -2 0 1
y 3 p 0
典题精讲
5 若点A (m,n)在一次函数y=3x+b 的图像上,且3m-n>2,则b 的取值范围为( )
A.b>2 B.b>-2
C.b<2 D.b<-2
D
6 一次函数y=-2x+m 的图像经过点P (-2,3),且与x 轴,y 轴分别交于点A,B,则△AOB 的面积是( )
A. B.
C.4 D.8
B
探索新知
3
知识点
用关系式法求一次函数表达式
例3 已知一次函数y=kx+b,当x=0时,y=1;当x=1时,y=0.试确定这个函数的表达式.
分别将x=0,y=1和x=1,y=0代入y=kx+b 中,
得到关于k、b 的二元一次方程组,解之即可.
将x=0,y=1和x=1,y=0分别代入y=kx+b,
得 解得
所以这个函数的表达式为y=-x+1.
导引:
解:
探索新知
总 结
满足一次函数表达式的一对对应值就是将一次函
数表达式作为方程时的一组解.将函数问题转化为方
程问题来解决.
典题精讲
1 一次函数的图像经过点A (1,2)和点B (-2,1),求这个函数的表达式.
设此一次函数的表达式为y=kx+b,把点(1,2),(-2,1)的坐标分别代入
得 解得
故这个函数的表达式为y=
解:
典题精讲
2 如果一次函数y =(k+3)x-13的图像上一点P 的坐标为(-5, 7),那么k 的值为_________.
3 一次函数的图像经过点(-1,-2)和( , 3).求函数的表达式.
-7
设一次函数的表达式为y=kx+b,将点(-1,-2),( , 3)的坐标分别代入,
可得 解得
所以此一次函数的表达式为y=
解:
典题精讲
4 已知一次函数的图像如图所示,求这个函数的表达式.
设这个函数的表达式为y=kx+b,
将点(0,2),(3,-4)的坐标分别
代入,
可得 解得
所以这个函数的表达式为y=-2x+2.
解:
典题精讲
5 已知y 是x 的一次函数,当x=3时,y=1;当x=-2时,y=-4.求这个一次函数的表达式.
设这个一次函数的表达式为y=kx+b (k≠0),将x=3,y=1和x=-2,y=-4分别代入上式得
可得 解得
所以这个函数的表达式为y=x-2.
解:
典题精讲
6 已知y+2与x-1成正比例,且当x=3时,y=4.
(1)求y 与x 之间的函数表达式;
(2)当y=1时,求x 的值.
(1)设y+2=k (x-1)(k≠0),把x=3,y=4代入,得4+2=k (3-1),解得k=3.
则y 与x 之间的函数表达式是y+2=3(x-1),
即y=3x-5.
(2)当y=1时,3x-5=1,解得x=2.
解:
典题精讲
7 根据下列条件,分别确定y 关于x 的函数表达式.
(1)y 与x 成正比例,且当x=9时,y=16;
(2)已知一次函数y=kx+b,当x=3时,y=2;当x=-2时,y=1.
(1)设y=k ′x (k ′≠0),把x=9,y=16代入,得16=9k ′,k ′= ,所以y= x.
解:
典题精讲
(2)把x=3,y=2和x=-2,y=1分别代入y=kx+b,
得 解得
所以y=
易错提醒
已知函数y=(n+3)x |n |-2是一次函数,则n=_______.
易错点:忽略一次函数中的k≠0这一条件导致错误.
3
学以致用
小试牛刀
1 若一个正比例函数的图像经过A (3,-6),B (m,-4)
两点,则m 的值为( )
A.2 B.8
C.-2 D.-8
A
小试牛刀
2 如图,直线y= x+4与x 轴,y 轴分别交于点A 和点B,点C,D 分别是线段AB,OB 的中点,点P 为OA上一动点,当PC+PD最小时,点P 的坐标为( )
A.(-3,0)
B.(-6,0)
C.
D.
C
小试牛刀
3
在平面直角坐标系中,一次函数y=kx+b (k,b 都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当-2<x ≤3时,求y 的取值范围;
(2)已知点P (m,n)在该函数的图象上,且m-n=4,求点P 的坐标.
小试牛刀
将(1,0),(0,2)代入y=kx+b
得: 解得:
∴这个函数的表达式为:y=-2x+2.
(1)把x=-2代入y=-2x+2得,y=6,
把x=3代入y=-2x+2得,y=-4,
∴y 的取值范围是-4≤ y<6.
(2)∵点P (m,n )在该函数的图象上,∴n=-2m+2.
∵m-n=4,∴m-(-2m+2)=4,
解得m=2. ∴n=-2,∴点P 的坐标为(2,-2).
解:
小试牛刀
4
如图,直线y= x+ 与两坐标轴分别交于A,B 两点.
(1)求∠ABO 的度数;
(2)过A 的直线l 交x 轴正半轴于C,AB=AC,求直线 l 对应的函数表达式.
小试牛刀
(1)对于直线y= x+ ,
令x=0,则y= ,
令y=0,则x=-1,
故点A 的坐标为(0, ),点B 的坐标为(-1,0),
则AO= ,BO=1,
∴AB= =2. ∴BO= AB,
∴∠BAO=30°. ∴∠ABO=60°.
解:
小试牛刀
(2)在△ABC 中,
∵AB=AC,AO⊥BC,
∴BO=CO,
则C 点的坐标为(1,0),
设直线l 对应的函数表达式为:y=kx+b (k,b为常数),
则 解得:
即直线 l 对应的函数表达式为:y=- x+ .
小试牛刀
5
小明受“乌鸦喝水”故事的启发,利用量桶和体积相同
的小球进行了如下操作:
请根据图中给出的信息,解答下列问题.
(1)放入一个小球,量桶中水面升高________cm;
(2)求放入小球后量桶中水面的高度y (cm)关于小球个
数x (个)的一次函数表达式(水未溢出,不要求写出
自变量的取值范围);
(3)量桶中至少放入几个小球时有水溢出?
2
小试牛刀
(2)设一次函数表达式为y=kx+b (k≠0).
把x=0,y=30及x=3,y=36分别代入函数解析
式,得 解得
即y=2x+30.
(3)由题意得2x+30>49,解得x>9.5.
因为x 是正整数,所以量桶中至少放入10个小球
时有水溢出.
解:
小试牛刀
6
小明对学校所添置的一批课桌、凳子进行观察后,发现它们可以根据人的身高来调节高度.于是,他测量了一套课桌、凳子相对应的四档高度,得到如下数据:
(1)小明经过对数据的探究发现:桌高y 是凳高x 的一次函数,请你求出这个函数的表达式(不要求写出x 的取值范围);
(2)小明回家后,测量了家里的写字台和凳子.写字台的高度为77 cm,凳子的高度为43.5 cm,请你判断它们是否配套,并说明理由.
档次 高度 第一档 第二档 第三档 第四档
凳高x (cm) 37.0 40.0 42.0 45.0
桌高y (cm) 70.0 74.8 78.0 82.8
小试牛刀
(1)设所求一次函数的表达式为y=kx+b (k,b 为常数,k≠0),任取表中的两组数据,不妨取(37.0,70.0)和(42.0,78.0)分别代入,
得 解得
∴所求一次函数的表达式为y=1.6x+10.8.
(2)不配套.理由:当x=43.5时,
y=1.6×43.5+10.8=80.4.
∵77≠80.4,∴不配套.
解:
课堂小结
课堂小结
用待定系数法求一次函数表达式要明确两点:
(1)具备条件:一次函数y=kx+b 中有两个不确定的系数k,b,需要两个独立的条件确定两个关于k,b 的方程,联立方程,解方程组求得k,b 的值.这两个条件通常是两个点的坐标或两对x,y 的值.
(2)确定方法:将两对已知变量的对应值分别代入y=kx+b 中,建立关于k,b 的方程组,通过解这个方程组,求出k,b,从而确定其表达式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
