【班海精品】冀教版(新)八下-21.4 一次函数的应用 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-21.4 一次函数的应用 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览











文档简介
(共51张PPT)
21.4 一次函数的应用
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
一天,小明以80米/分的速度去上学,请问小明离家
的距离S (米)与小明出发的时间t (分)之间的函数关系式是
怎样的?它是一次函数吗?它是正比例函数吗?S=80t
(t ≥0)下面的图像能表示上面问题中的S 与t 的关系吗?
1
S (米)
t (分)
O
80
新课精讲
探索新知
1
知识点
从函数图像中获取信息的应用
某电脑工程师张先生准备开一家小型电脑公司,欲租
一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,
每月租金为3 000元;乙家未装修,每月租金为2 000元,但
若装修成与甲家房屋同样的规格,则需要花装修费4万元.
(1)设租用时间为x 个月,承租房屋所付租金为y 元,分别求
租用甲、 乙两家的租金y 与租用时间x 之间的函数关系式.
(2)根据求出的两个函数表达式,试判断租用哪家的房屋更合算.
探索新知
小亮的做法
(1)租用甲家房屋时,y=3 000x,租用乙家房屋时,y =
2 000x+40 000.
(2)①由 3 000x=2 000x+40 000,解得x=40.
即当租用40个月时,无论是租用哪一家,租金都相同.
②由3 000x>2 000x+40 000,解得x>40.
即当租用时间超过40个月时, 租乙家的房屋更合算.
③由3 000x<2 000x+40 000,解得x<40.
即当租用时间少于40个月时, 租甲家的房屋更合算.
探索新知
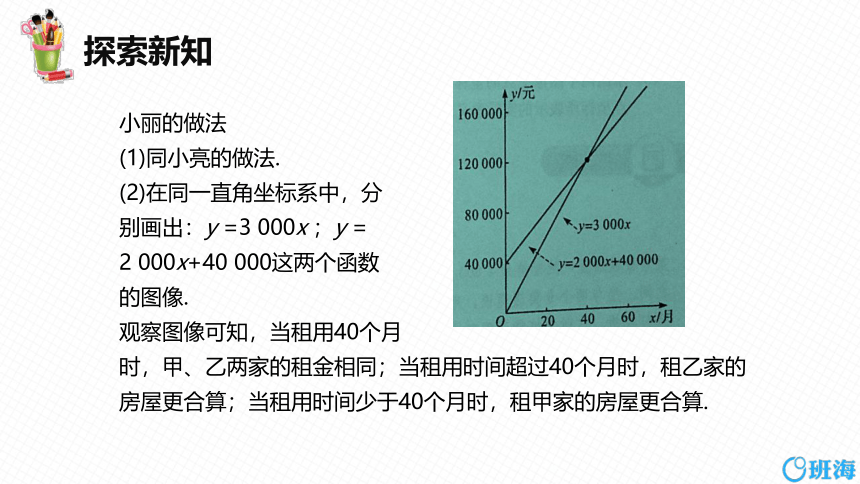
小丽的做法
(1)同小亮的做法.
(2)在同一直角坐标系中,分
别画出:y =3 000x ;y =
2 000x+40 000这两个函数
的图像.
观察图像可知,当租用40个月
时,甲、乙两家的租金相同;当租用时间超过40个月时,租乙家的房屋更合算;当租用时间少于40个月时,租甲家的房屋更合算.
探索新知
例1 甲骑自行车以10 km/h的速度沿公路行驶,出发3h后,乙骑摩托车从同一地点出发沿公路与甲同向行驶.速度为25 km/h.
(1)设甲离开出发地的时间为x (h).求:
①甲离开出发地的路程y (km)与x (h)之间的函数关系式,并指出自变量x 的取值范围.
②乙离开出发地的路程.y (km)与x (h)之间的函数关系式,并指出自变量x 的取值范围.
(2)在同一直角坐标系中,画出(1)中两个函数的图像,并结合实际问题,解释两图像交点的意义.
探索新知
(1)由公式s=vt,得
①甲离开出发地的路程y 与x 的函数关系式为
y =10x.
自变量x 的取值范围为x ≥0.
②乙离开出发地的路程y 与x 的函数关系式为
y =25(x-3),即y =25x-75.
自变量x 的取值范围为x ≥3.
解:
探索新知
(2)以上两个函数的图像如图所示.两个函数图像的交点
坐标是(5,50),即甲出发5 h后被乙追上(或乙出发
2 h后追上甲). 此时,两人距离出发地50 km.
探索新知
总 结
本题考查了一次函数的应用,主要利用了路程、速度、时间三者之间的关系和相遇问题中的等量关系,从图像中准确获取信息是解题的关键.
典题精讲
1 A,B两地相距36 km,甲、乙二人分别从A地和B地同时出发,相向而行.他们距A地的路程s (km)和出发后的时间t (h)之间的函数关系的图像如图所示.
(1)甲行驶了几小时到达B地,
乙行驶了几小时到达A地?
(2)分别写出甲、乙二人距A地
的路程s 与时间t 之间的函数
关系式.
(3)求出两个图像交点的坐标,并解释交点坐标所表示的实际意义.
典题精讲
(1)甲行驶了4.5 h到达B地,乙行驶了6 h到达A地.
(2)s甲=8t (0≤ t ≤4.5),s乙=-6t+36(0≤ t ≤6).
(3)令8t=-6t+36,解得t= ,当t= 时,s甲=s乙
=8× = ,所以交点坐标为 ,实际意义:纵坐标表示二人相遇时距A地 km,横坐标表示二人行驶了 h时相遇.
解:
典题精讲
2 甲、乙两商店销售同一种产品的销售价y (元)与销售量x (件)之间的图像如图所示.下列说法:
①买2件甲、乙两家销售价一样;
②买1件乙家的合算;
③买3件甲家的合算;
④买乙家的1件销售价约为3元.
其中所有正确的说法是( )
A.①② B.②③④
C.②③ D.①②③
D
典题精讲
3 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y (km)与行驶时间t (h)的函数图像如图所示,下列说法正确的有( )
①甲车的速度为50 km/h
②乙车用了3 h到达B城
③甲车出发4 h时,乙车追上甲车
④乙车出发后经过1 h或3 h两车相距50 km
A.1个 B.2个 C.3个 D.4个
D
探索新知
2
知识点
从图表中获取信息的应用
例2 为保障我国海外维和部队官兵的生活,现需通过A 港口、B港口分别运送100吨和50吨生活物资,已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如下表所示.
港口 费用/(元/吨) 甲仓库 乙仓库
A 14 20
B 10 8
探索新知
(1)第一步,先用含x 的式子表示出从甲仓库运往B 港口的物资的
吨数,以及从乙仓库运往A、B 两港口的物资吨数;第二步,
根据运输的总费用等于四条运输路线的费用总和,便可求出总
费用y (元)与x (吨)之间的函数关系式;第三步,根据问题的实
际意义列出不等式组,即可求得x 的取值范围.
(2)根据一次函数的增减性及自变量的取值范围,即可确定总费
用最低时的物资调配方案和最低总费用.
(1)设从甲仓库运送到A 港口的物资为x 吨,求总费用y (元)与x (吨)之间的函数关系式,并写出x 的取值范围.
(2)求出最低总费用,并说明总费用最低时的调配方案.
导引:
探索新知
(1)因为从甲仓库运送到A 港口的物资为x 吨,所以从甲仓库运往B 港口的有(80-x )吨;从乙仓库运往A 港口的有(100-x )吨,运往B 港口的有50-(80-x )=x-30(吨),
所以y=14x+20(100-x )+10(80-x )+8(x-30)=2560-8x,x 的取值范围是30≤ x ≤80.
(2)由(1)得y=2560-8x,y 随x 增大而减小,所以当x=80时总运费最低,为y=2560-8×80=1920,此时的调配方案为:把甲仓库的全部物资运往A 港口,再从乙仓库运20吨往A 港口,乙仓库余下的物资全部运往B 港口.
解:
探索新知
总 结
解此类题的关键是理清各种等量关系,能利用等量关系列出函数关系式,能利用函数的增减性求最值.注意要正确运用一次函数y=kx+b 的增减性:当k>0时,y 随x 的增大而增大,当k<0时,y 随x 的增大而减小.
典题精讲
1 某工厂开发生产一种新产品,前期投入150 000元.生产时,每件成本为25元,每件销售价为40元.设生产x 件时,总成本(包括前期投入)为m 元,销售额为n 元.
(1)分别求出m,n 与x 之间的函数关系式.
(2)至少生产并销售多少件产品后,工厂才会有盈利?
典题精讲
(1)m=25x+150 000(x 为正整数);
n=40x (x 为正整数).
(2)当n>m 时工厂才会有盈利,
即40x>25x+150 000,解得x>10 000.
故至少生产并销售10 000件产品后,工厂才会有盈利.
解:
典题精讲
2 某学校欲购置一批标价为4 800元的某型号电脑,需求数量在15至25台之间.经与两个专卖店商谈,甲店同意打八折;乙店承诺先赠一台,其余打九折.这所学校购买哪家的电脑更合算?
典题精讲
设从甲店买需y1元,从乙店买需y2元,购买电脑的数量为x 台,则y1=4 800x ×80%=3 840x,即y1=3 840x (15≤ x ≤25,且x 为整数);y2=4 800(x-1)×90%=4 320x-4 320,即y2=4 320x-4 320
(15≤ x ≤25,且x 为整数).y1-y2=3 840x-(4 320x-4 320)=
-480x+4 320(15≤ x ≤25,且x 为整数).所以y1-y2的值随x 的增大而减小,当x=15时,y1-y2有最大值,而当x=15时.
y1-y2=-480×15+4 320=-2 880<0,所以这所学校购买甲店的电脑更合算.
解:
典题精讲
3 某工厂有甲、乙两个净化水池,容积都是480 m3.注满乙池的水得到净化可以使用时,甲池未净化的水已有192 m3.此时,乙池以10 m3/h的速度将水放出使用,而甲池仍以8 m3/h的速度注水.设乙池放水为x h 时,甲、乙两池中的水量用y m3表示.
(1)分别写出甲、乙两池中的水量y 关于x 的函数关系式及自变量x 的取值范围,并在同一直角坐标系中画出这两个函数的图像.
典题精讲
(2)借助由(1)得出的图像回答:
①当x 取何值时,甲、乙两池水量相等?
②当x 取哪些值时,甲池的水量少于乙池的水量?
③当x 取哪些值时,甲池的水董多于乙池的水量?
典题精讲
(1)甲池中的水量y=8x+192(0≤x≤36);乙池中的水量y=480-10x (0≤ x ≤48).
所画函数图像如图所示.
(2)①x=16;②0≤x<16;③16<x ≤36.
解:
典题精讲
4 某种子商店销售一种小麦种子,为促销,推出了两种销售方案供采购者选择.方案一:小麦种子的价格为4元/千克,无论购买多少均不打折.方案二:购买3 kg以内(含3 kg),价格为5元/千克;若一次性购买超过3 kg,则超过3 kg的部分价格打七折.
(1)求出方案一中购买的小麦种子的数量x (kg)和付款金额y (元)之间的函数关系式.
(2)若你去购买一定量的这种小麦种子,你会选择哪个方案?说明理由.
典题精讲
(1)y=4x (x ≥0).
(2)由题意得,方案二中,若购买不超过3 kg,则付款金额y (元)与购买的小麦种子的数量x (kg)之间的函数关系式为y=5x (0≤ x ≤3);若一次性购买超过3 kg,则付款金额y (元)与购买的小麦种子的数量x (kg)之间的函数关系式为y=3×5+(x-3)×5×70%=3.5x+4.5,即y=3.5x+4.5(x>3).当0≤ x ≤3时,4x<5x,即当购买不超过3 kg时,选择方案一购买;
解:
典题精讲
当x>3时,令3.5x+4.5=4x,解得x=9.即当一次性购买9 kg时,两方案付款金额一样;令3.5x+4.5>4x,解得x<9.即当一次性购买大于3 kg小于9 kg时,选择方案一购买;令3.5x+4.5<4x,解得x>9,即当一次性购买超过9 kg时,选择方案二购买.
综上可知:当购买不足9 kg时,选择方案一购买,当购买9 kg时,两方案付款金额一样;当购买超过9 kg时,选择方案二购买.
典题精讲
5 某学校的复印任务原来由甲复印社承接,其收费y (元)与复印页数x (页)的关系如下表:
(1)已知y 与x 满足一次函数关系,求该函数表达式;
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费.乙复印社每月收费y (元)与复印页数x (页)之间的函数表达式为____________(不需要写出自变量的取值范围);
x /页 … 100 200 400 1 000 …
y /元 … 40 80 160 400 …
典题精讲
(3)在如图所示的直角坐标系内画出(1)(2)中的函数图像,并回答每月复印页数在1 200页左右时,选择哪个复印社更合算?
典题精讲
(1)根据表中的数据可知y 是x 的正比例函数,设y=kx.将x=100,y=40代入y=kx,得k=0.4,
所以该函数表达式为y=0.4x.
(2)y=0.15x+200
(3)画函数图像如图所示.
由图像可知,当每月复
印页数在1 200页左右时,
选择乙复印社更合算.
解:
典题精讲
6 公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.
(1)设租用甲种货车x 辆(x 为非负整数),试填写表格.
租用甲种货车的数量/辆 3 7 x
租用的甲种货车最多运送机器的数量/台 135
租用的乙种货车最多运送机器的数量/台 150
表一
典题精讲
(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
租用甲种货车的数量/辆 3 7 x
租用甲种货车的费用/元 2 800
租用乙种货车的费用/元 280
表二
典题精讲
(1)表一:315;45x;30;-30x+240
表二:1 200;400x;1 400;-280x+2 240
(2)能完成此项运送任务的最节省费用的租车方案是甲种货车6辆,乙种货车2辆.理由:当租用甲种货车x 辆时,设两种货车的总费用为y 元,则y=400x+(-280x+2 240)=120x+2 240.
又因为45x+(-30x+240)≥330,所以x ≥6.
因为120>0,所以在函数y=120x+2 240中,y 随x 的增大而增大.
所以当x=6时,y 取得最小值,
即能完成此项运送任务的最节省费用的租车方案是甲种货车6辆,乙种货车2辆.
解:
学以致用
小试牛刀
1 一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网所用的时间计费;方式B除收月基本费20元外,再以每分0.05元的价格按上网所用时间计费.若上网所用时间为x min,计费为y 元,如图是在同一坐标系中,分别描述两种计费方式的函数图像,有下列结论:①图像甲描述的是方式A;②图像乙描述的是方式B;③当上网所用时间是
500 min时,选择方式B省钱.其中,
结论正确的有( )
A.3个 B.2个
C.1个 D.0个
A
小试牛刀
2
某商店分两次购进A、B 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量/件 购进所需
费用/元
A B 第一次 30 40 3 800
第二次 40 30 3 200
小试牛刀
(1)求A、B 两种商品每件的进价分别是多少元.
(2)商场决定A 种商品以每件30元出售,B 种商品以每
件100元出售.为满足市场需求,需购进A、B 两种
商品共1 000件,且A 种商品的数量不少于B 种商品
数量的4倍,请你求出获利最大的进货方案,并确
定最大利润.
小试牛刀
(1)设A 种商品每件的进价为x 元,
B 种商品每件的进价为y 元,
根据题意得
解得
答:A 种商品每件的进价为20元,
B 种商品每件的进价为80元.
解:
小试牛刀
(2)设购进B 种商品m 件,获得的利润为w 元,
则购进A 种商品(1 000-m )件,
根据题意得w=(30-20)(1 000-m)+(100-80)m
=10m+10 000.
∵A 种商品的数量不少于B 种商品数量的4倍,
∴1 000-m ≥4m,
解得m ≤ 200.
小试牛刀
∵在w=10m+10 000中,k=10>0,
∴w 的值随m 的增大而增大,
∴当m=200时,w取最大值,
最大值为10×200+10 000=12 000.
答:当购进A 种商品800件,B 种商品200件时,
销售利润最大,最大利润为12 000元.
小试牛刀
3
江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x (单位:元)之间
的函数关系如图所示:
小试牛刀
(1)直接写出y甲,y乙关于x 的函数关系式;
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱?
(1)y甲=0.8x;
y乙=
解:
小试牛刀
(2)当0<x<2 000时,0.8x<x,到甲商店购买更省钱;
当x ≥2 000时,若到甲商店购买更省钱,
则0.8x<0.7x+600,解得x<6 000.
若到乙商店购买更省钱,
则0.8x>0.7x+600,解得x>6 000;
若到甲、乙两商店购买花钱一样,
则0.8x=0.7x+600,解得x=6 000;
解:
小试牛刀
故当购买金额按原价小于6 000元时,
到甲商店购买更省钱;
当购买金额按原价大于6 000元时,
到乙商店购买更省钱;
当购买金额按原价等于6 000元时,
到甲、乙两商店购买花钱一样.
课堂小结
课堂小结
1. 在同一问题中,有时会同时出现两个一次函数,这时我们要通过两个函数之间的关系,及在特殊情况下的函数值来解决实际问题.
2. 若在同一直角坐标系中,同时出现两个一次函数的图像,要利用这两个图像的位置关系、交点坐标以及与坐标轴交点的坐标等有关信息解决问题.利用两个一次函数图像可以解决利润最大、成本最小、话费最少、运费最省、是否合算等问题,这些问题我们可以利用函数的图像进行比较,为此归纳如下数学模型:
课堂小结
已知一次函数y1,y2,y3(自变量x 均大于或等于0)的图像如图,它们交点的横坐标分别为a,b,c.
当0当b当x >c 时,y3当x=a 时,y1=y2;
当x=b 时,y1=y3;
当x=c 时,y2=y3.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
21.4 一次函数的应用
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
一天,小明以80米/分的速度去上学,请问小明离家
的距离S (米)与小明出发的时间t (分)之间的函数关系式是
怎样的?它是一次函数吗?它是正比例函数吗?S=80t
(t ≥0)下面的图像能表示上面问题中的S 与t 的关系吗?
1
S (米)
t (分)
O
80
新课精讲
探索新知
1
知识点
从函数图像中获取信息的应用
某电脑工程师张先生准备开一家小型电脑公司,欲租
一处临街房屋.现有甲、乙两家出租屋,甲家已经装修好,
每月租金为3 000元;乙家未装修,每月租金为2 000元,但
若装修成与甲家房屋同样的规格,则需要花装修费4万元.
(1)设租用时间为x 个月,承租房屋所付租金为y 元,分别求
租用甲、 乙两家的租金y 与租用时间x 之间的函数关系式.
(2)根据求出的两个函数表达式,试判断租用哪家的房屋更合算.
探索新知
小亮的做法
(1)租用甲家房屋时,y=3 000x,租用乙家房屋时,y =
2 000x+40 000.
(2)①由 3 000x=2 000x+40 000,解得x=40.
即当租用40个月时,无论是租用哪一家,租金都相同.
②由3 000x>2 000x+40 000,解得x>40.
即当租用时间超过40个月时, 租乙家的房屋更合算.
③由3 000x<2 000x+40 000,解得x<40.
即当租用时间少于40个月时, 租甲家的房屋更合算.
探索新知
小丽的做法
(1)同小亮的做法.
(2)在同一直角坐标系中,分
别画出:y =3 000x ;y =
2 000x+40 000这两个函数
的图像.
观察图像可知,当租用40个月
时,甲、乙两家的租金相同;当租用时间超过40个月时,租乙家的房屋更合算;当租用时间少于40个月时,租甲家的房屋更合算.
探索新知
例1 甲骑自行车以10 km/h的速度沿公路行驶,出发3h后,乙骑摩托车从同一地点出发沿公路与甲同向行驶.速度为25 km/h.
(1)设甲离开出发地的时间为x (h).求:
①甲离开出发地的路程y (km)与x (h)之间的函数关系式,并指出自变量x 的取值范围.
②乙离开出发地的路程.y (km)与x (h)之间的函数关系式,并指出自变量x 的取值范围.
(2)在同一直角坐标系中,画出(1)中两个函数的图像,并结合实际问题,解释两图像交点的意义.
探索新知
(1)由公式s=vt,得
①甲离开出发地的路程y 与x 的函数关系式为
y =10x.
自变量x 的取值范围为x ≥0.
②乙离开出发地的路程y 与x 的函数关系式为
y =25(x-3),即y =25x-75.
自变量x 的取值范围为x ≥3.
解:
探索新知
(2)以上两个函数的图像如图所示.两个函数图像的交点
坐标是(5,50),即甲出发5 h后被乙追上(或乙出发
2 h后追上甲). 此时,两人距离出发地50 km.
探索新知
总 结
本题考查了一次函数的应用,主要利用了路程、速度、时间三者之间的关系和相遇问题中的等量关系,从图像中准确获取信息是解题的关键.
典题精讲
1 A,B两地相距36 km,甲、乙二人分别从A地和B地同时出发,相向而行.他们距A地的路程s (km)和出发后的时间t (h)之间的函数关系的图像如图所示.
(1)甲行驶了几小时到达B地,
乙行驶了几小时到达A地?
(2)分别写出甲、乙二人距A地
的路程s 与时间t 之间的函数
关系式.
(3)求出两个图像交点的坐标,并解释交点坐标所表示的实际意义.
典题精讲
(1)甲行驶了4.5 h到达B地,乙行驶了6 h到达A地.
(2)s甲=8t (0≤ t ≤4.5),s乙=-6t+36(0≤ t ≤6).
(3)令8t=-6t+36,解得t= ,当t= 时,s甲=s乙
=8× = ,所以交点坐标为 ,实际意义:纵坐标表示二人相遇时距A地 km,横坐标表示二人行驶了 h时相遇.
解:
典题精讲
2 甲、乙两商店销售同一种产品的销售价y (元)与销售量x (件)之间的图像如图所示.下列说法:
①买2件甲、乙两家销售价一样;
②买1件乙家的合算;
③买3件甲家的合算;
④买乙家的1件销售价约为3元.
其中所有正确的说法是( )
A.①② B.②③④
C.②③ D.①②③
D
典题精讲
3 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y (km)与行驶时间t (h)的函数图像如图所示,下列说法正确的有( )
①甲车的速度为50 km/h
②乙车用了3 h到达B城
③甲车出发4 h时,乙车追上甲车
④乙车出发后经过1 h或3 h两车相距50 km
A.1个 B.2个 C.3个 D.4个
D
探索新知
2
知识点
从图表中获取信息的应用
例2 为保障我国海外维和部队官兵的生活,现需通过A 港口、B港口分别运送100吨和50吨生活物资,已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如下表所示.
港口 费用/(元/吨) 甲仓库 乙仓库
A 14 20
B 10 8
探索新知
(1)第一步,先用含x 的式子表示出从甲仓库运往B 港口的物资的
吨数,以及从乙仓库运往A、B 两港口的物资吨数;第二步,
根据运输的总费用等于四条运输路线的费用总和,便可求出总
费用y (元)与x (吨)之间的函数关系式;第三步,根据问题的实
际意义列出不等式组,即可求得x 的取值范围.
(2)根据一次函数的增减性及自变量的取值范围,即可确定总费
用最低时的物资调配方案和最低总费用.
(1)设从甲仓库运送到A 港口的物资为x 吨,求总费用y (元)与x (吨)之间的函数关系式,并写出x 的取值范围.
(2)求出最低总费用,并说明总费用最低时的调配方案.
导引:
探索新知
(1)因为从甲仓库运送到A 港口的物资为x 吨,所以从甲仓库运往B 港口的有(80-x )吨;从乙仓库运往A 港口的有(100-x )吨,运往B 港口的有50-(80-x )=x-30(吨),
所以y=14x+20(100-x )+10(80-x )+8(x-30)=2560-8x,x 的取值范围是30≤ x ≤80.
(2)由(1)得y=2560-8x,y 随x 增大而减小,所以当x=80时总运费最低,为y=2560-8×80=1920,此时的调配方案为:把甲仓库的全部物资运往A 港口,再从乙仓库运20吨往A 港口,乙仓库余下的物资全部运往B 港口.
解:
探索新知
总 结
解此类题的关键是理清各种等量关系,能利用等量关系列出函数关系式,能利用函数的增减性求最值.注意要正确运用一次函数y=kx+b 的增减性:当k>0时,y 随x 的增大而增大,当k<0时,y 随x 的增大而减小.
典题精讲
1 某工厂开发生产一种新产品,前期投入150 000元.生产时,每件成本为25元,每件销售价为40元.设生产x 件时,总成本(包括前期投入)为m 元,销售额为n 元.
(1)分别求出m,n 与x 之间的函数关系式.
(2)至少生产并销售多少件产品后,工厂才会有盈利?
典题精讲
(1)m=25x+150 000(x 为正整数);
n=40x (x 为正整数).
(2)当n>m 时工厂才会有盈利,
即40x>25x+150 000,解得x>10 000.
故至少生产并销售10 000件产品后,工厂才会有盈利.
解:
典题精讲
2 某学校欲购置一批标价为4 800元的某型号电脑,需求数量在15至25台之间.经与两个专卖店商谈,甲店同意打八折;乙店承诺先赠一台,其余打九折.这所学校购买哪家的电脑更合算?
典题精讲
设从甲店买需y1元,从乙店买需y2元,购买电脑的数量为x 台,则y1=4 800x ×80%=3 840x,即y1=3 840x (15≤ x ≤25,且x 为整数);y2=4 800(x-1)×90%=4 320x-4 320,即y2=4 320x-4 320
(15≤ x ≤25,且x 为整数).y1-y2=3 840x-(4 320x-4 320)=
-480x+4 320(15≤ x ≤25,且x 为整数).所以y1-y2的值随x 的增大而减小,当x=15时,y1-y2有最大值,而当x=15时.
y1-y2=-480×15+4 320=-2 880<0,所以这所学校购买甲店的电脑更合算.
解:
典题精讲
3 某工厂有甲、乙两个净化水池,容积都是480 m3.注满乙池的水得到净化可以使用时,甲池未净化的水已有192 m3.此时,乙池以10 m3/h的速度将水放出使用,而甲池仍以8 m3/h的速度注水.设乙池放水为x h 时,甲、乙两池中的水量用y m3表示.
(1)分别写出甲、乙两池中的水量y 关于x 的函数关系式及自变量x 的取值范围,并在同一直角坐标系中画出这两个函数的图像.
典题精讲
(2)借助由(1)得出的图像回答:
①当x 取何值时,甲、乙两池水量相等?
②当x 取哪些值时,甲池的水量少于乙池的水量?
③当x 取哪些值时,甲池的水董多于乙池的水量?
典题精讲
(1)甲池中的水量y=8x+192(0≤x≤36);乙池中的水量y=480-10x (0≤ x ≤48).
所画函数图像如图所示.
(2)①x=16;②0≤x<16;③16<x ≤36.
解:
典题精讲
4 某种子商店销售一种小麦种子,为促销,推出了两种销售方案供采购者选择.方案一:小麦种子的价格为4元/千克,无论购买多少均不打折.方案二:购买3 kg以内(含3 kg),价格为5元/千克;若一次性购买超过3 kg,则超过3 kg的部分价格打七折.
(1)求出方案一中购买的小麦种子的数量x (kg)和付款金额y (元)之间的函数关系式.
(2)若你去购买一定量的这种小麦种子,你会选择哪个方案?说明理由.
典题精讲
(1)y=4x (x ≥0).
(2)由题意得,方案二中,若购买不超过3 kg,则付款金额y (元)与购买的小麦种子的数量x (kg)之间的函数关系式为y=5x (0≤ x ≤3);若一次性购买超过3 kg,则付款金额y (元)与购买的小麦种子的数量x (kg)之间的函数关系式为y=3×5+(x-3)×5×70%=3.5x+4.5,即y=3.5x+4.5(x>3).当0≤ x ≤3时,4x<5x,即当购买不超过3 kg时,选择方案一购买;
解:
典题精讲
当x>3时,令3.5x+4.5=4x,解得x=9.即当一次性购买9 kg时,两方案付款金额一样;令3.5x+4.5>4x,解得x<9.即当一次性购买大于3 kg小于9 kg时,选择方案一购买;令3.5x+4.5<4x,解得x>9,即当一次性购买超过9 kg时,选择方案二购买.
综上可知:当购买不足9 kg时,选择方案一购买,当购买9 kg时,两方案付款金额一样;当购买超过9 kg时,选择方案二购买.
典题精讲
5 某学校的复印任务原来由甲复印社承接,其收费y (元)与复印页数x (页)的关系如下表:
(1)已知y 与x 满足一次函数关系,求该函数表达式;
(2)现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费.乙复印社每月收费y (元)与复印页数x (页)之间的函数表达式为____________(不需要写出自变量的取值范围);
x /页 … 100 200 400 1 000 …
y /元 … 40 80 160 400 …
典题精讲
(3)在如图所示的直角坐标系内画出(1)(2)中的函数图像,并回答每月复印页数在1 200页左右时,选择哪个复印社更合算?
典题精讲
(1)根据表中的数据可知y 是x 的正比例函数,设y=kx.将x=100,y=40代入y=kx,得k=0.4,
所以该函数表达式为y=0.4x.
(2)y=0.15x+200
(3)画函数图像如图所示.
由图像可知,当每月复
印页数在1 200页左右时,
选择乙复印社更合算.
解:
典题精讲
6 公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.
(1)设租用甲种货车x 辆(x 为非负整数),试填写表格.
租用甲种货车的数量/辆 3 7 x
租用的甲种货车最多运送机器的数量/台 135
租用的乙种货车最多运送机器的数量/台 150
表一
典题精讲
(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
租用甲种货车的数量/辆 3 7 x
租用甲种货车的费用/元 2 800
租用乙种货车的费用/元 280
表二
典题精讲
(1)表一:315;45x;30;-30x+240
表二:1 200;400x;1 400;-280x+2 240
(2)能完成此项运送任务的最节省费用的租车方案是甲种货车6辆,乙种货车2辆.理由:当租用甲种货车x 辆时,设两种货车的总费用为y 元,则y=400x+(-280x+2 240)=120x+2 240.
又因为45x+(-30x+240)≥330,所以x ≥6.
因为120>0,所以在函数y=120x+2 240中,y 随x 的增大而增大.
所以当x=6时,y 取得最小值,
即能完成此项运送任务的最节省费用的租车方案是甲种货车6辆,乙种货车2辆.
解:
学以致用
小试牛刀
1 一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网所用的时间计费;方式B除收月基本费20元外,再以每分0.05元的价格按上网所用时间计费.若上网所用时间为x min,计费为y 元,如图是在同一坐标系中,分别描述两种计费方式的函数图像,有下列结论:①图像甲描述的是方式A;②图像乙描述的是方式B;③当上网所用时间是
500 min时,选择方式B省钱.其中,
结论正确的有( )
A.3个 B.2个
C.1个 D.0个
A
小试牛刀
2
某商店分两次购进A、B 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量/件 购进所需
费用/元
A B 第一次 30 40 3 800
第二次 40 30 3 200
小试牛刀
(1)求A、B 两种商品每件的进价分别是多少元.
(2)商场决定A 种商品以每件30元出售,B 种商品以每
件100元出售.为满足市场需求,需购进A、B 两种
商品共1 000件,且A 种商品的数量不少于B 种商品
数量的4倍,请你求出获利最大的进货方案,并确
定最大利润.
小试牛刀
(1)设A 种商品每件的进价为x 元,
B 种商品每件的进价为y 元,
根据题意得
解得
答:A 种商品每件的进价为20元,
B 种商品每件的进价为80元.
解:
小试牛刀
(2)设购进B 种商品m 件,获得的利润为w 元,
则购进A 种商品(1 000-m )件,
根据题意得w=(30-20)(1 000-m)+(100-80)m
=10m+10 000.
∵A 种商品的数量不少于B 种商品数量的4倍,
∴1 000-m ≥4m,
解得m ≤ 200.
小试牛刀
∵在w=10m+10 000中,k=10>0,
∴w 的值随m 的增大而增大,
∴当m=200时,w取最大值,
最大值为10×200+10 000=12 000.
答:当购进A 种商品800件,B 种商品200件时,
销售利润最大,最大利润为12 000元.
小试牛刀
3
江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x (单位:元)之间
的函数关系如图所示:
小试牛刀
(1)直接写出y甲,y乙关于x 的函数关系式;
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱?
(1)y甲=0.8x;
y乙=
解:
小试牛刀
(2)当0<x<2 000时,0.8x<x,到甲商店购买更省钱;
当x ≥2 000时,若到甲商店购买更省钱,
则0.8x<0.7x+600,解得x<6 000.
若到乙商店购买更省钱,
则0.8x>0.7x+600,解得x>6 000;
若到甲、乙两商店购买花钱一样,
则0.8x=0.7x+600,解得x=6 000;
解:
小试牛刀
故当购买金额按原价小于6 000元时,
到甲商店购买更省钱;
当购买金额按原价大于6 000元时,
到乙商店购买更省钱;
当购买金额按原价等于6 000元时,
到甲、乙两商店购买花钱一样.
课堂小结
课堂小结
1. 在同一问题中,有时会同时出现两个一次函数,这时我们要通过两个函数之间的关系,及在特殊情况下的函数值来解决实际问题.
2. 若在同一直角坐标系中,同时出现两个一次函数的图像,要利用这两个图像的位置关系、交点坐标以及与坐标轴交点的坐标等有关信息解决问题.利用两个一次函数图像可以解决利润最大、成本最小、话费最少、运费最省、是否合算等问题,这些问题我们可以利用函数的图像进行比较,为此归纳如下数学模型:
课堂小结
已知一次函数y1,y2,y3(自变量x 均大于或等于0)的图像如图,它们交点的横坐标分别为a,b,c.
当0
当x=b 时,y1=y3;
当x=c 时,y2=y3.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
