【班海精品】冀教版(新)八下-21.5 一次函数与二元一次方程的关系【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-21.5 一次函数与二元一次方程的关系【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览








文档简介
(共53张PPT)
21.5 一次函数与二元一次方程的关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
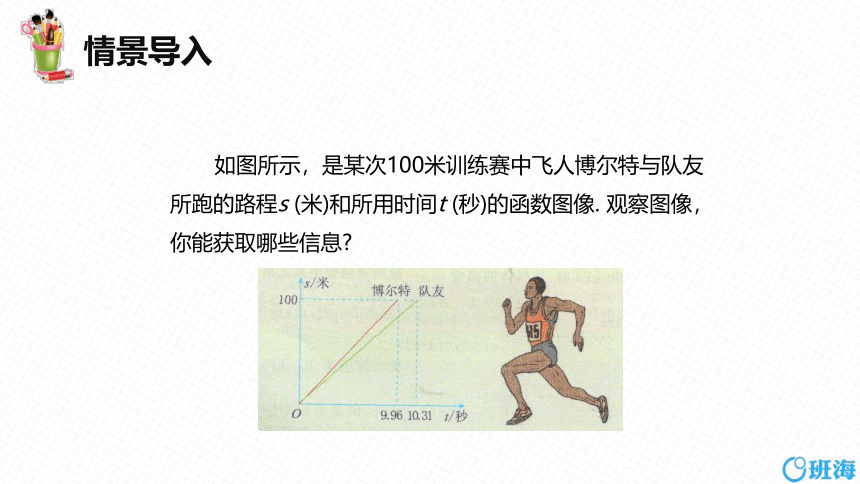
如图所示,是某次100米训练赛中飞人博尔特与队友所跑的路程s (米)和所用时间t (秒)的函数图像. 观察图像,你能获取哪些信息
新课精讲
探索新知
1
知识点
一次函数与二元一次方程的关系
二元一次方程 y –x =1有多少个解?你能写出方程的几组解吗?
二元一次方程 y –x =1可以写成一次函数吗?
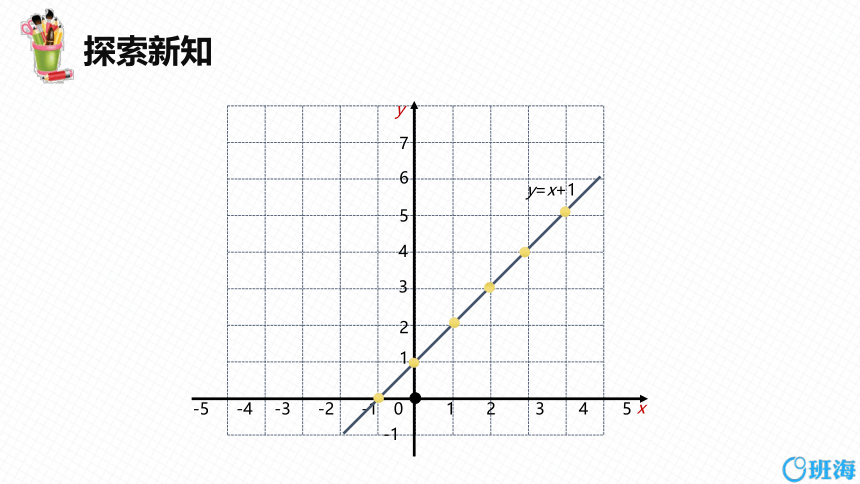
3. 画出一次函数 y =x+1的图像。
4. 把1题中方程的几组解为坐标的点在3题坐标系上描出来,你发现了什么?
5. 一次函数y=x+1的图像上的点的坐标适合二元一次方程 y –x =1吗?
探索新知
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
y=x+1
探索新知
以二元一次方程的解为坐标的点都在相应的函数图像上.
反过来,一次函数图像上的点的坐标都是相应的二元一次方程的解.
探索新知
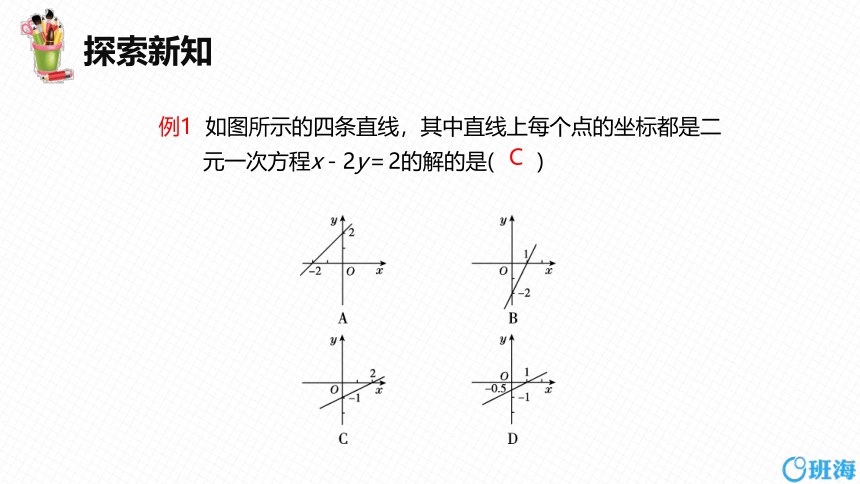
例1 如图所示的四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )
C
探索新知
对于二元一次方程x-2y=2,当x=0时,y=-1;当y=0时,x=2,故直线x-2y=2与两坐标轴的交点坐标是(0,-1),(2,0).对照四个选项中的直线,可知选C.
导引:
探索新知
总 结
直线y=kx+b 与x 轴的交点的横坐标即是二元一
次方程y=kx+b 中,当y=0时x 的值;直线y=kx+b
与y 轴的交点的纵坐标即是二元一次方程y=kx+b 中,
当x=0时y 的值.解这类题,常运用数形结合思想.
典题精讲
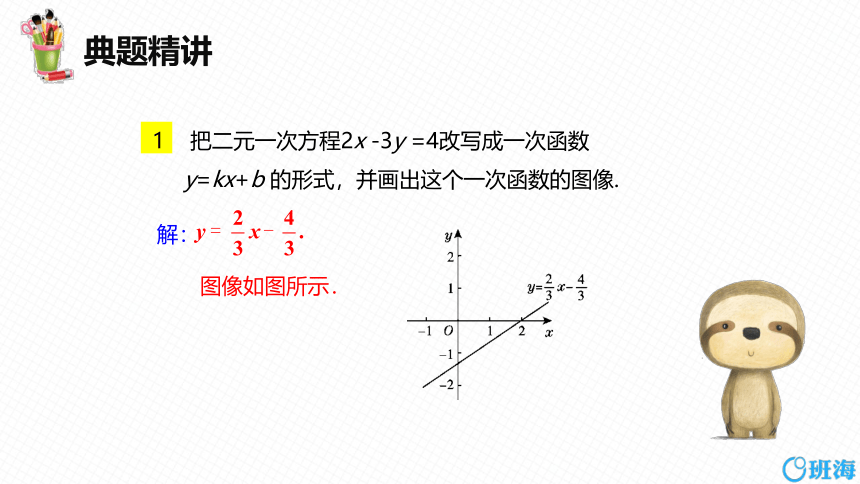
1 把二元一次方程2x -3y =4改写成一次函数y=kx+b 的形式,并画出这个一次函数的图像.
图像如图所示.
解:
典题精讲
2 写出二元一次方程2x –y =1的三个解,以方程的解为坐标在直角坐标系中画点,这些点是否都在一次函数y =2x-1的图像上?
2x-y=1的解有
画图略.
这些点均在一次函数y=2x-1的图像上.
解:
典题精讲
3 把二元一次方程2(x-3)+y =0改写成一次函数y=kx+b 的形式,并画出这个一次函数的图像.
y=-2x+6.图像如图所示.
解:
典题精讲
4 以二元一次方程3x-4y=8的解为坐标的所有点组成的图像也是一次函数y=____________的图像.
5 下面四条直线,其中直线上每个点的坐标都是二元一次方程2x-y=2的解的是( )
B
探索新知
2
知识点
一次函数与二元一次方程组的关系
探究一次函数与二元一次方程组的关系
1. 解方程组
2. 在同一直角坐标系中画出一次函数y =x+1和y =-x+1
的图像。
探索新知
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
y=x+1
y=-x+1
(0,1)
x+y=1
-x+y=1
是否任意两个一次函数的交点坐标都是它们所对应的二元一次方程组的解?
探索新知
二元一次方程组的解是这两个方程所对应的一次
函数图像的交点坐标。
反之,两个一次函数图像的交点坐标是这两个一
次函数所对应的二元一次方程组的解。
想一想
若二元一次方程组无解,那么这两个方程所对应
的一次函数图像是怎样的?
探索新知
例2 利用图像法解二元一次方程组:
列表得:
过点(0,-2)和(1,1)画出直线 l1,再过点(0,2)和
(1,1)画出直线 l2,如图所示,
由图像知两条直线交点的坐标为
(1,1),∴原方程组的解为
x 0 1
y=3x-2 -2 1
y=2-x 2 2
解:
探索新知
总 结
用图像法解二元一次方程组的基本步骤:
(1)将方程组中的两个方程转化成一次函数y=kx+b 的形式;
(2)在同一直角坐标系中画出两函数的图像;
(3)利用图像的直观性确定交点坐标.
典题精讲
1 已知一次函数y=ax+5和y=-x+b 的图像交于点P (1,2).
(1)直接写出方程组 的解.
(2)求a,b 的值.
(1)
(2)将 代入 可得
所以a=-3,b=3.
解:
典题精讲
2 解方程组 并由此指出在同一直角坐标系内,一次函数y=2x-2与y=-2x+6图像交点的坐标.
解方程组得
由此得两函数图像交点的坐标为(2,2).
解:
典题精讲
3 已知一次函数y1=2x-1和y2=-x-1的图像如图所示,根据图像填空.当x_______时,y1=y2;当
x________时,y1<y2;方程组 的解是________.
=0
<0
典题精讲
4 如图,过点Q (0,3.5)的一次函数的图像与正比例函数y=2x 的图像相交于点P,能表示这个一次函数图像的方程是( )
A.3x-2y+3.5=0
B.3x-2y-3.5=0
C.3x-2y+7=0
D.3x+2y-7=0
D
典题精讲
5 若二元一次方程y=2x+a 与y=-x+b 对应的直线都经过点A (-2,0),且与y 轴分别交于点B,C,则△ABC 的面积是( )
A.4 B.5
C.6 D.7
C
典题精讲
6 用图像法解方程组 正确的是( )
C
典题精讲
7 如图,函数y=2x 和y=ax+4的图像相交于点A (m,3),则不等式2x ≥ax+4的解集为( )
A.x ≤3 B.x ≥3
C.x ≤ D.x ≥
D
探索新知
例3 已知一次函数y=ax+2与y=kx+b 的图像交于点A,如图所示,且方程组 的解为
点B 的坐标为(0,-1),请你确定这两个一次函
数的表达式.
要确定这两个一次函数的表
达式,需确定交点A 的坐标,
而交点A 的坐标即为已知方程
组的解.因此用待定系数法可求得k,
b,a 的值,进而确定两个一次函数的表达式.
导引:
探索新知
因为方程组 的解为
所以交点A 的坐标为(2,1),
所以2a+2=1,解得a=- .
又因为函数y=kx+b 的图像过交点A (2,1)和点B (0,-1),
所以 解得
所以这两个一次函数的表达式分别为y=- x+2,
y=x-1.
解:
探索新知
总 结
“交点”是解决问题的关键,从“形”的角度讲,它是两个函数图像的公共点即自变量值相等时函数值也相等的点;从“数”的角度讲,它是两个函数表达式的公共解,即二元一次方程组的解.
典题精讲
已知关于x,y 的方程组 的解为
(1)写出一次函数y=-x+1和的图像交点P 的坐标.
(2)若这两个函数的图像与x 轴分别交于点A,B,
求S △ABP
典题精讲
(1) P (-1,2).
(2)一次函数y=-x+1的图像与x 轴的交点坐标为(1,0),将(-1,2)代入y=- x + ,可得2=- ×(-1)+ ,解得a=-2.一次函数y= x+ 的图像与x 轴的交点坐标为(-4,0).所以AB=5.所以S△ABP= ×5×2=5.
解:
易错提醒
用图像法解方程组
易错点:审题不仔细,没有按照要求解题.
由x+2y=4,可得y=- x+2.
由x-y=1,可得y=x-1.
在同一直角坐标系内作出一次函数y=- x+2的图像 l1 和y=x-1的图像 l2,如图所示,通过观察可得 l1 和 l2
的交点坐标为(2,1).
所以原方程组的解为
解:
学以致用
小试牛刀
1 若二元一次方程3x-2y=1所对应的直线是l,则下列各点不在直线 l 上的是( )
A.(1,1) B.(-1,-1)
C.(-3,-5) D.
B
小试牛刀
2 用一次函数y1=kx+b 与y2=x+a 的图像如图所示,则下列结论:①k<0;②a>0;③x<3时,y1<y2;
④方程组 的解是
其中正确的个数是( )
A.1 B.2
C.3 D.4
B
小试牛刀
3
在同一平面直角坐标系内画出二元一次方程2x-y-2=0和x-y+3=0所对应的一次函数的图像.利用图像求:
(1)方程2x-2=x+3的解;
(2)方程组 的解.
小试牛刀
画出函数y=2x-2和y=x+3的图像,如图所示.
(1)根据图像可知方程2x-2=x+3的解为x=5.
(2)根据图像可知
方程组
的解为
解:
解题策略:
关键是正确画出图像,把握好方程、方程组与函数图像的关系.
小试牛刀
4
在直角坐标系中,直线 l1 经过点(1,-3)和(3,1),直线 l2 经过点(1,0),且与直线 l1 交于点A (2,a).
(1)求a 的值.
(2)A (2,a )可看成怎样的二元一次方程组的解?
(3)设直线 l1 与y 轴交于点B,直线 l2 与 y 轴交于点C,
求△ABC 的面积.
小试牛刀
(1)设直线 l1 的表达式为y=k1x+b1,
将点(1,-3)和(3,1)的坐标代入y=k1x+b1,
得 解得
所以直线 l1 的表达式为y=2x-5.
将点(2,a )的坐标代入y=2x-5,
得a=4-5=-1.
解:
小试牛刀
(3)将x=0代入y=2x-5,得y=-5,
所以B (0,-5),
将x=0代入y=-x+1,得y=1,所以C (0,1),
所以BC=6,
所以S△ABC= ×6×2=6.
小试牛刀
(2)设直线 l2 的表达式为y=k2x+b2,
将点(1,0)和(2,-1)的坐标代入y=k2x+b2,
得 解得
所以直线 l2 的表达式为y=-x+1.
所以点A (2,a )可看作是二元一次方程组
的解.
小试牛刀
5
甲、乙两车从A 城出发前往B 城,在整个行程中,两车离开A 城的距离y 与时刻t 的对应关系如图所示.
(1)A,B 两城之间的距离是多少千米?
(1)由图像知,A,B
两城之间的距离是
300 km.
解:
小试牛刀
(2)设过(5,0),(10,300)的直线对应的函数表达式为
y甲=k1t+b1,则 解得
所以y甲=60t-300.
设过(6,0),(9,300)的直线对应的函数表达式为
y乙=k2t+b2,则 解得
所以y乙=100t-600.
解:
(2)求乙车出发后多长时间追上甲车.
小试牛刀
当y甲=y乙,即60t-300=100t-600时,t=7.5.
所以7.5-6=1.5(h).
所以乙车出发后1.5 h 追上甲车.
(3)甲车出发后 h或2 h或3 h或 h后,
两车相距20 km.
小试牛刀
6
为更新果树品种,某果园计划购进A,B 两个品种的果树苗栽植培育.若计划购进这两种果树苗共45棵,其中A 种树苗的价格为7元/棵,购买B 种树苗所需费用y (元)与购买数量x (棵)之间存在如图所示的函数关系.
小试牛刀
(1)求y 与x 的函数关系式;
(2)若在购买计划中,B 种树苗的数量不超过35棵,但不少于A 种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.
(1)当0≤x<20时,因为图像经过点(0,0)和(20,160),
所以设y=k1x,把(20,160)代入,
得160=20k1,解得k1=8;
解:
小试牛刀
当x ≥20时,设y=k2x+b,
把(20,160)和(40,288)分别代入,
得 解得
所以y 与x 的函数关系式是
y= (其中x 为整数).
小试牛刀
(2)依题意,得
解得22.5≤ x ≤35,
此时y=6.4x+32.
设总费用为z 元,依题意,
得z=y+7(45-x )=6.4x+32+315-7x
=-0.6x+347,
小试牛刀
因为-0.6<0,所以z 随x 的增大而减小.
因为22.5≤ x ≤35,且x 为整数,
所以当x=35时,z 最小,
此时z=-0.6×35+347=326,45-x=10.
所以购买A 种树苗10棵,B 种树苗35棵时,
总费用最低,最低费用为326元.
课堂小结
课堂小结
1. 二元一次方程组无解 一次函数的图像平行(无交点);
二元一次方程组有一组解 一次函数的图像相交(有一个交点) ;
二元一次方程组有无数组解 一次函数的图像重合(有无数个交点).
2. 一次函数与二元一次方程之间的区别和联系:
区别:(1)二元一次方程有两个未知数,而一次函数有两个变量;
(2)二元一次方程是用一个等式表示两个未知数的关系,而一次函数既可以用一个等式表示两个变量之间的关系,又可以用表格或图像来表示两个变量之间的关系.
联系:在平面直角坐标系中分别描出以二元一次方程的解为坐标的点,这些点都在相应的一次函数的图像上.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
21.5 一次函数与二元一次方程的关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图所示,是某次100米训练赛中飞人博尔特与队友所跑的路程s (米)和所用时间t (秒)的函数图像. 观察图像,你能获取哪些信息
新课精讲
探索新知
1
知识点
一次函数与二元一次方程的关系
二元一次方程 y –x =1有多少个解?你能写出方程的几组解吗?
二元一次方程 y –x =1可以写成一次函数吗?
3. 画出一次函数 y =x+1的图像。
4. 把1题中方程的几组解为坐标的点在3题坐标系上描出来,你发现了什么?
5. 一次函数y=x+1的图像上的点的坐标适合二元一次方程 y –x =1吗?
探索新知
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
y=x+1
探索新知
以二元一次方程的解为坐标的点都在相应的函数图像上.
反过来,一次函数图像上的点的坐标都是相应的二元一次方程的解.
探索新知
例1 如图所示的四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )
C
探索新知
对于二元一次方程x-2y=2,当x=0时,y=-1;当y=0时,x=2,故直线x-2y=2与两坐标轴的交点坐标是(0,-1),(2,0).对照四个选项中的直线,可知选C.
导引:
探索新知
总 结
直线y=kx+b 与x 轴的交点的横坐标即是二元一
次方程y=kx+b 中,当y=0时x 的值;直线y=kx+b
与y 轴的交点的纵坐标即是二元一次方程y=kx+b 中,
当x=0时y 的值.解这类题,常运用数形结合思想.
典题精讲
1 把二元一次方程2x -3y =4改写成一次函数y=kx+b 的形式,并画出这个一次函数的图像.
图像如图所示.
解:
典题精讲
2 写出二元一次方程2x –y =1的三个解,以方程的解为坐标在直角坐标系中画点,这些点是否都在一次函数y =2x-1的图像上?
2x-y=1的解有
画图略.
这些点均在一次函数y=2x-1的图像上.
解:
典题精讲
3 把二元一次方程2(x-3)+y =0改写成一次函数y=kx+b 的形式,并画出这个一次函数的图像.
y=-2x+6.图像如图所示.
解:
典题精讲
4 以二元一次方程3x-4y=8的解为坐标的所有点组成的图像也是一次函数y=____________的图像.
5 下面四条直线,其中直线上每个点的坐标都是二元一次方程2x-y=2的解的是( )
B
探索新知
2
知识点
一次函数与二元一次方程组的关系
探究一次函数与二元一次方程组的关系
1. 解方程组
2. 在同一直角坐标系中画出一次函数y =x+1和y =-x+1
的图像。
探索新知
x
y
0
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
y=x+1
y=-x+1
(0,1)
x+y=1
-x+y=1
是否任意两个一次函数的交点坐标都是它们所对应的二元一次方程组的解?
探索新知
二元一次方程组的解是这两个方程所对应的一次
函数图像的交点坐标。
反之,两个一次函数图像的交点坐标是这两个一
次函数所对应的二元一次方程组的解。
想一想
若二元一次方程组无解,那么这两个方程所对应
的一次函数图像是怎样的?
探索新知
例2 利用图像法解二元一次方程组:
列表得:
过点(0,-2)和(1,1)画出直线 l1,再过点(0,2)和
(1,1)画出直线 l2,如图所示,
由图像知两条直线交点的坐标为
(1,1),∴原方程组的解为
x 0 1
y=3x-2 -2 1
y=2-x 2 2
解:
探索新知
总 结
用图像法解二元一次方程组的基本步骤:
(1)将方程组中的两个方程转化成一次函数y=kx+b 的形式;
(2)在同一直角坐标系中画出两函数的图像;
(3)利用图像的直观性确定交点坐标.
典题精讲
1 已知一次函数y=ax+5和y=-x+b 的图像交于点P (1,2).
(1)直接写出方程组 的解.
(2)求a,b 的值.
(1)
(2)将 代入 可得
所以a=-3,b=3.
解:
典题精讲
2 解方程组 并由此指出在同一直角坐标系内,一次函数y=2x-2与y=-2x+6图像交点的坐标.
解方程组得
由此得两函数图像交点的坐标为(2,2).
解:
典题精讲
3 已知一次函数y1=2x-1和y2=-x-1的图像如图所示,根据图像填空.当x_______时,y1=y2;当
x________时,y1<y2;方程组 的解是________.
=0
<0
典题精讲
4 如图,过点Q (0,3.5)的一次函数的图像与正比例函数y=2x 的图像相交于点P,能表示这个一次函数图像的方程是( )
A.3x-2y+3.5=0
B.3x-2y-3.5=0
C.3x-2y+7=0
D.3x+2y-7=0
D
典题精讲
5 若二元一次方程y=2x+a 与y=-x+b 对应的直线都经过点A (-2,0),且与y 轴分别交于点B,C,则△ABC 的面积是( )
A.4 B.5
C.6 D.7
C
典题精讲
6 用图像法解方程组 正确的是( )
C
典题精讲
7 如图,函数y=2x 和y=ax+4的图像相交于点A (m,3),则不等式2x ≥ax+4的解集为( )
A.x ≤3 B.x ≥3
C.x ≤ D.x ≥
D
探索新知
例3 已知一次函数y=ax+2与y=kx+b 的图像交于点A,如图所示,且方程组 的解为
点B 的坐标为(0,-1),请你确定这两个一次函
数的表达式.
要确定这两个一次函数的表
达式,需确定交点A 的坐标,
而交点A 的坐标即为已知方程
组的解.因此用待定系数法可求得k,
b,a 的值,进而确定两个一次函数的表达式.
导引:
探索新知
因为方程组 的解为
所以交点A 的坐标为(2,1),
所以2a+2=1,解得a=- .
又因为函数y=kx+b 的图像过交点A (2,1)和点B (0,-1),
所以 解得
所以这两个一次函数的表达式分别为y=- x+2,
y=x-1.
解:
探索新知
总 结
“交点”是解决问题的关键,从“形”的角度讲,它是两个函数图像的公共点即自变量值相等时函数值也相等的点;从“数”的角度讲,它是两个函数表达式的公共解,即二元一次方程组的解.
典题精讲
已知关于x,y 的方程组 的解为
(1)写出一次函数y=-x+1和的图像交点P 的坐标.
(2)若这两个函数的图像与x 轴分别交于点A,B,
求S △ABP
典题精讲
(1) P (-1,2).
(2)一次函数y=-x+1的图像与x 轴的交点坐标为(1,0),将(-1,2)代入y=- x + ,可得2=- ×(-1)+ ,解得a=-2.一次函数y= x+ 的图像与x 轴的交点坐标为(-4,0).所以AB=5.所以S△ABP= ×5×2=5.
解:
易错提醒
用图像法解方程组
易错点:审题不仔细,没有按照要求解题.
由x+2y=4,可得y=- x+2.
由x-y=1,可得y=x-1.
在同一直角坐标系内作出一次函数y=- x+2的图像 l1 和y=x-1的图像 l2,如图所示,通过观察可得 l1 和 l2
的交点坐标为(2,1).
所以原方程组的解为
解:
学以致用
小试牛刀
1 若二元一次方程3x-2y=1所对应的直线是l,则下列各点不在直线 l 上的是( )
A.(1,1) B.(-1,-1)
C.(-3,-5) D.
B
小试牛刀
2 用一次函数y1=kx+b 与y2=x+a 的图像如图所示,则下列结论:①k<0;②a>0;③x<3时,y1<y2;
④方程组 的解是
其中正确的个数是( )
A.1 B.2
C.3 D.4
B
小试牛刀
3
在同一平面直角坐标系内画出二元一次方程2x-y-2=0和x-y+3=0所对应的一次函数的图像.利用图像求:
(1)方程2x-2=x+3的解;
(2)方程组 的解.
小试牛刀
画出函数y=2x-2和y=x+3的图像,如图所示.
(1)根据图像可知方程2x-2=x+3的解为x=5.
(2)根据图像可知
方程组
的解为
解:
解题策略:
关键是正确画出图像,把握好方程、方程组与函数图像的关系.
小试牛刀
4
在直角坐标系中,直线 l1 经过点(1,-3)和(3,1),直线 l2 经过点(1,0),且与直线 l1 交于点A (2,a).
(1)求a 的值.
(2)A (2,a )可看成怎样的二元一次方程组的解?
(3)设直线 l1 与y 轴交于点B,直线 l2 与 y 轴交于点C,
求△ABC 的面积.
小试牛刀
(1)设直线 l1 的表达式为y=k1x+b1,
将点(1,-3)和(3,1)的坐标代入y=k1x+b1,
得 解得
所以直线 l1 的表达式为y=2x-5.
将点(2,a )的坐标代入y=2x-5,
得a=4-5=-1.
解:
小试牛刀
(3)将x=0代入y=2x-5,得y=-5,
所以B (0,-5),
将x=0代入y=-x+1,得y=1,所以C (0,1),
所以BC=6,
所以S△ABC= ×6×2=6.
小试牛刀
(2)设直线 l2 的表达式为y=k2x+b2,
将点(1,0)和(2,-1)的坐标代入y=k2x+b2,
得 解得
所以直线 l2 的表达式为y=-x+1.
所以点A (2,a )可看作是二元一次方程组
的解.
小试牛刀
5
甲、乙两车从A 城出发前往B 城,在整个行程中,两车离开A 城的距离y 与时刻t 的对应关系如图所示.
(1)A,B 两城之间的距离是多少千米?
(1)由图像知,A,B
两城之间的距离是
300 km.
解:
小试牛刀
(2)设过(5,0),(10,300)的直线对应的函数表达式为
y甲=k1t+b1,则 解得
所以y甲=60t-300.
设过(6,0),(9,300)的直线对应的函数表达式为
y乙=k2t+b2,则 解得
所以y乙=100t-600.
解:
(2)求乙车出发后多长时间追上甲车.
小试牛刀
当y甲=y乙,即60t-300=100t-600时,t=7.5.
所以7.5-6=1.5(h).
所以乙车出发后1.5 h 追上甲车.
(3)甲车出发后 h或2 h或3 h或 h后,
两车相距20 km.
小试牛刀
6
为更新果树品种,某果园计划购进A,B 两个品种的果树苗栽植培育.若计划购进这两种果树苗共45棵,其中A 种树苗的价格为7元/棵,购买B 种树苗所需费用y (元)与购买数量x (棵)之间存在如图所示的函数关系.
小试牛刀
(1)求y 与x 的函数关系式;
(2)若在购买计划中,B 种树苗的数量不超过35棵,但不少于A 种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.
(1)当0≤x<20时,因为图像经过点(0,0)和(20,160),
所以设y=k1x,把(20,160)代入,
得160=20k1,解得k1=8;
解:
小试牛刀
当x ≥20时,设y=k2x+b,
把(20,160)和(40,288)分别代入,
得 解得
所以y 与x 的函数关系式是
y= (其中x 为整数).
小试牛刀
(2)依题意,得
解得22.5≤ x ≤35,
此时y=6.4x+32.
设总费用为z 元,依题意,
得z=y+7(45-x )=6.4x+32+315-7x
=-0.6x+347,
小试牛刀
因为-0.6<0,所以z 随x 的增大而减小.
因为22.5≤ x ≤35,且x 为整数,
所以当x=35时,z 最小,
此时z=-0.6×35+347=326,45-x=10.
所以购买A 种树苗10棵,B 种树苗35棵时,
总费用最低,最低费用为326元.
课堂小结
课堂小结
1. 二元一次方程组无解 一次函数的图像平行(无交点);
二元一次方程组有一组解 一次函数的图像相交(有一个交点) ;
二元一次方程组有无数组解 一次函数的图像重合(有无数个交点).
2. 一次函数与二元一次方程之间的区别和联系:
区别:(1)二元一次方程有两个未知数,而一次函数有两个变量;
(2)二元一次方程是用一个等式表示两个未知数的关系,而一次函数既可以用一个等式表示两个变量之间的关系,又可以用表格或图像来表示两个变量之间的关系.
联系:在平面直角坐标系中分别描出以二元一次方程的解为坐标的点,这些点都在相应的一次函数的图像上.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
