【班海精品】冀教版(新)八下-22.2 平行四边形的判定 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-22.2 平行四边形的判定 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览








文档简介
(共57张PPT)
22.2 平行四边形的判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
根据平行四边形的性质思考:对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
新课精讲
探索新知
知识点
由两组对边的关系判定平行四边形
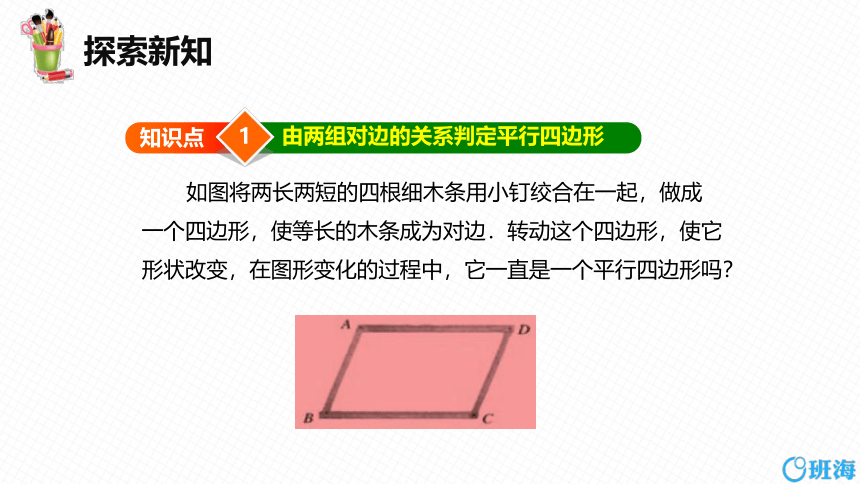
如图将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?
1
探索新知
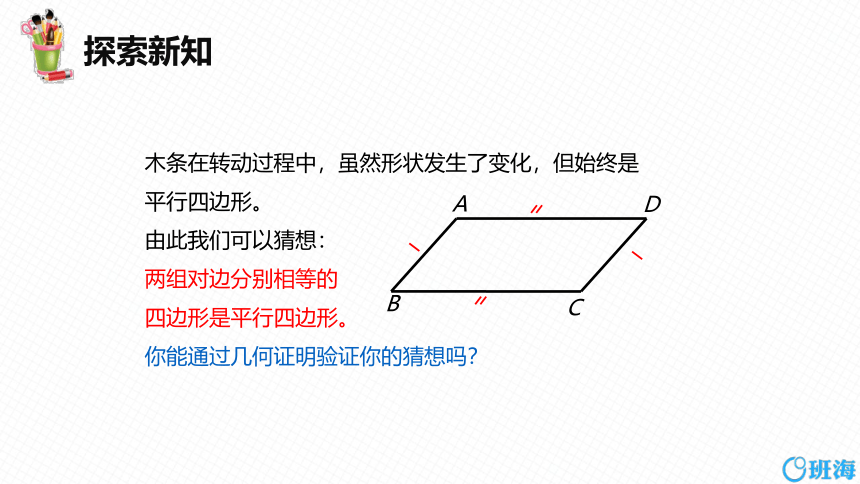
木条在转动过程中,虽然形状发生了变化,但始终是
平行四边形。
由此我们可以猜想:
两组对边分别相等的
四边形是平行四边形。
你能通过几何证明验证你的猜想吗?
B
C
A
D
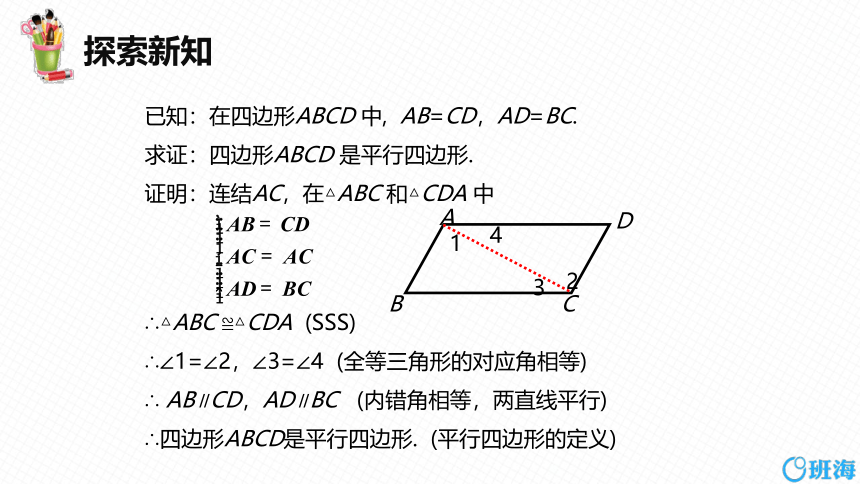
已知:在四边形ABCD 中, AB=CD,AD=BC.
求证:四边形ABCD 是平行四边形.
证明:连结AC,在△ABC 和△CDA 中
∴△ABC ≌△CDA (SSS)
∴∠1=∠2,∠3=∠4 (全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形. (平行四边形的定义)
探索新知
B
D
A
C
2
1
3
4
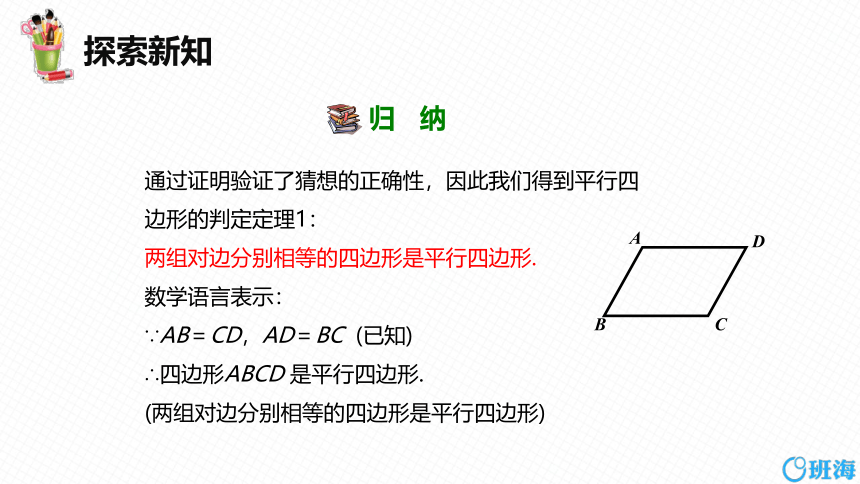
通过证明验证了猜想的正确性,因此我们得到平行四
边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
数学语言表示:
∵AB=CD,AD=BC (已知)
∴四边形ABCD 是平行四边形.
(两组对边分别相等的四边形是平行四边形)
探索新知
归 纳
B
D
A
C
探索新知
例1 如图,分别以△ABC 的三边为一边,在BC 的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF 是平行四边形.
导引:由等边三角形的性质可以得到线段相等,角相等,
进而可以通过全等三角形证明四边形ADEF 的两
组对边分别相等,最后根据两组对边分别相等的
四边形是平行四边形进行判定.
探索新知
∵△ABD、△BCE、△ACF 都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC.∴△DBE ≌△ABC.∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证△ABC ≌△FEC,∴AB=FE.∴FE=AD.
∴四边形ADEF 是平行四边形.
证明:
探索新知
总 结
解答本题时通过证明三角形全等得到四边形ADEF 的两组对边分别相等是关键.
典题精讲
已知:如图, AC 为 ABCD 的对角线,DE⊥AC,BF⊥AC,垂足分别为E,F.
求证:四边形DEBF 是平行四边形
典题精讲
在 ABCD 中,AD∥BC,AD=BC.
因为DE⊥AC,BF⊥AC,
所以∠DEA=∠DEF=∠BFE=∠BFC=90°,
因为AD∥BC,所以∠DAE=∠BCF,
在△ADE 和△CBF 中,
所以△ADE ≌△CBF,
所以DE=BF,因为∠DEF=∠BFE=90°,
所以DE∥BF,所以四边形DEBF 是平行四边形.
证明:
典题精讲
2 如图,已知三点A,B,C.画平行四边形,使其三个顶点分别是A,B,C.
解:略.
典题精讲
3 已知:如图,在 ABCD 的各边AB,BC,CD , DA上分别取点K,L, M,N,使AK=CM,BL=DN. 求证:四边形KLMN 是平行四边形.
典题精讲
在 ABCD 中,∠A=∠C,∠B=∠D,AB=CD,AD=BC,因为AK=CM,所以DM=BK,
在△NDM 和△LBK 中,
所以△NDM ≌△LBK.
所以MN=KL,
同理可得NK=ML,
所以四边形KLMN 是平行四边形.
证明:
典题精讲
四边形的四条边长分别是a,b,c,d,其中a,b 为一组对边长,c,d 为另一组对边长且a 2+b 2+c 2+d 2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线互相垂直的四边形
4
B
典题精讲
下列图形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个锐角三角形
D.两个全等三角形
5
D
探索新知
2
知识点
由对角线互相平分判定平行四边形
通过前面的学习,我们知道,平行四边形的对边相
等、对角相等、对角线互相平分.反过来,对边相等,或
对角相等,或对角线互相平分的四边形是平行四边形吗?
也就是说,平行四边形的性质定理的逆命题成立吗?
下面我们以“对角线互相平分的四边形是平行四边
形”为例,通过三角形 全等进行证明.
思考
探索新知
如图,在四边形ABCD 中,AC,BD 相交于点O,
且OA=OC,OB=OD.
求证:四边形ABCD 是平行四边形.
∵OA=OC,OD=OB,
∠AOD=∠COB,
∴△ AOD ≌△COB.
∴∠OAD =∠OCB.
∴AD//BC.
同理 AB//DC.
∴四边形ABCD 是平行四边形.
证明:
A
B
C
D
O
探索新知
归 纳
平行四边形的判定定理3:
两条对角线互相平分的四边形是平行四边形.
符号语言:如图,
在四边形ABCD 中,
∵AO=CO,BO=DO,
∴四边形ABCD 是平行四边形.
探索新知
例2 已知:如图, ABCD 的两条对角线AC,BD 相交于点O,E,F 分别为OA,OC 的中点.
求证:四边形EBFD 是平行四边形.
证明:∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵E,F 分别为OA,OC 的中点.
∴OE=OF.
∴四边形EBFD 是平行四边形.
探索新知
总 结
从对角线方面判断四边形的形状要注意是对角线互相平分,即交点既是第一条对角线的中点,又是第二条对角线的中点.
典题精讲
1 已知:如图, ABCD 的对角线AC,BD 相交于点O,EF 过点O 交AD 于点E,交BC 于点F,G 是OA 的中点,H 是OC 的中点.
求证:四边形EGFH 是平行四边形.
典题精讲
解:在 ABCD 中,AD∥BC,OA=OC,
因为AD∥BC,所以∠EAO=∠FCO,
在△AEO 和△CFO 中,
所以△AEO ≌△CFO,
所以EO=FO,
因为G 是OA 的中点,H 是OC 的中点,
所以OG=OH= OA= OC,
所以四边形EGFH 是平行四边形.
典题精讲
如图,四边形ABCD 的对角线相交于点O,AO=CO,请添加一个条件______________(只添一个即可),使四边形ABCD 是平行四边形.
2
BO=DO
典题精讲
如图,在四边形ABCD 中,对角线AC,BD 相交于点O,下列条件不能判定四边形ABCD 为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
3
C
探索新知
知识点
平行四边形判定方法的综合应用
例3 如图,四边形ABCD 是平行四边形,E,F 为对角线AC 上两点,连接ED,EB,FD,FB.给出以下条件:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
导引:欲证明∠1=∠2,只需证
得四边形BFDE 是平行四边
形或△ABF ≌△CDE 即可.
3
探索新知
选取条件①BE∥DF.
证明:如图,∵BE∥DF,
∴∠BEC=∠DFA.∴∠BEA=∠DFC.
∵四边形ABCD 是平行四边形,∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
在△ABE 与△CDF 中,
∴△ABE ≌△CDF (AAS).∴BE=DF.
又∵BE∥DF,∴四边形BFDE 是平行四边形.
∴ED∥BF.∴∠1=∠2.
解:
探索新知
选取条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD 是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAF=∠DCE.
在△ABF 与△CDE 中,
∴△ABF ≌△CDE (SAS).∴∠1=∠2.
探索新知
总 结
平行四边形判定方法综合起来有多种,具体选择哪种方法判定要取决于题目中给出的条件,最终目的都是为了简单、方便的判定四边形是平行四边形.
典题精讲
1 已知:如图,在四边形ABCD 中,对角线AC,BD 相交于点O.仅从下列条件中任意选取两项作为已知条件,能够判定四边形ABCD 是平行四边形的有哪些?
①AB∥CD;②BC=AD;
③AB=CD; ④BC∥AD;
⑤OA=OC; ⑥OB=OD.
解:①③,①④,①⑤,①⑥,②③,②④,④⑤,④⑥,⑤⑥均能够判定四边形ABCD 是平行四边形.
典题精讲
2 已知:如图,D,E 分别为△ABC 的边AB 和AC 的中点,延长AE 到点F,使EF=DE,连接CF.
求证:四边形BCFD 是平行四边形.
典题精讲
如图,连接AF,DC.
由点D,E分别为△ABC 的边AB 和边AC 的中点,
得AD=BD,AE=EC,
由AE=CE,DE=EF
可得四边形ADCF 是平行四边形,
所以AD∥CF,AD=CF,
又因为AD=BD,所以BD=CF,
又因为BD∥CF,所以四边形BCFD 是平行四边形.
证明:
典题精讲
3 如图,在 ABCD 中,E 为BC 边上一点.试在AD 边上找一点F,使四边形AECF 是平行四边形,并说明理由.
解:在AD 边上找一点F,当满足AF=EC 时,可使得四边形AECF 是平行四边形.说明理由略.
A
B
C
D
E
典题精讲
下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
4
D
易错提醒
如图,在 ABCD 中,对角线AC,BD 相交于O,E,F是对角线上的两点,给出下列4个条件:
①OE=OF; ②DE=BF;
③∠ADE=∠CBF;
④∠ABE=∠CDF.
其中不能判定四边形DEBF 是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个
易错点:混淆平行四边形的判定方法致判断错误.
B
学以致用
小试牛刀
在四边形ABCD 中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD 中任选两个使四边形ABCD 为平行四边形的选法有( )
A.3种 B.4种
C.5种 D.6种
1
B
小试牛刀
如图,在四边形ABCD 中,对角线AC,BD 相交于E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD 的面积为( )
A.6 B.12
C.20 D.24
2
D
小试牛刀
在四边形ABCD 中,对角线AC,BD 相交于点O,给出下列4组条件:
①AB∥CD,AD∥BC;②AB=CD,AD=BC;
③AO=CO,BO=DO;④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组 B.2组
C.3组 D.4组
3
C
小试牛刀
4
如图,在△ABC 中,∠ABC=90°,∠BAC=60°,△ACD 是等边三角形,E 是AC 的中点,连接BE 并延长,交DC 于点F,求证:
(1)△ABE ≌△CFE;
(2)四边形ABFD 是平行四边形.
小试牛刀
(1)∵△ACD 是等边三角形,
∴∠DCA=60°.
又∵∠BAC=60°,
∴∠DCA=∠BAC.
∵E 是AC 的中点,
∴AE=CE.
在△ABE 与△CFE 中,
∴△ABE ≌△CFE.
证明:
小试牛刀
(2)∵E 是AC 的中点,∴AE= AC.
在Rt△ABC 中,∠ABC=90°,∠BAC=60°,
∴∠ACB=30°,∴AB= AC.
∴AB=AE.
∴△ABE 是等边三角形.
∴△CFE 是等边三角形.
∴∠CFE=60°.
解:
小试牛刀
∵△ACD 是等边三角形,
∴∠CDA=60°.
∴∠CFE=∠CDA.
∴BF∥AD.
又由(1)知∠DCA=∠BAC,
∴AB∥CD.
∴四边形ABFD 是平行四边形.
小试牛刀
如图,在 ABCD 中,点E,F 在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF 是平行四边形.
5
小试牛刀
(1)∵四边形ABCD 是平行四边形.
∴AD∥CB,AD=CB.∴∠DAE=∠BCF.
在△ADE 和△CBF 中,
∴△ADE ≌△CBF. ∴DE=BF.
(2)如图,连接BD,交AC 于点O,
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OE=OF.
∴四边形DEBF 是平行四边形.
证明:
小试牛刀
6
已知:如图,E,F 分别为 ABCD 中AD,BC 的中点,连接AF,BE 交于点G,连接CE,DF 交于点H.
求证:EF 与GH 互相平分.
小试牛刀
∵E 为AD 的中点,F 为BC 的中点,
∴AE= AD,CF= BC.
∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC.
∴AE∥CF,AE=CF.
∴四边形AFCE 是平行四边形.
∴AF∥CE. 同理可证BE∥DF.
∴四边形GFHE 是平行四边形.
∴EF 与GH 互相平分.
证明:
小试牛刀
7
如图,已知点E,C 在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC ≌△DEF;
(2)试判断四边形AECD 的形状,并证明你的结论.
小试牛刀
(1) ∵AB∥DE,
∴∠B=∠DEF.
∵BE=EC=CF,∴BC=EF.
在△ABC 和△DEF 中,
∴△ABC ≌△DEF.
证明:
小试牛刀
(2) 四边形AECD 是平行四边形.
证明:∵△ABC ≌△DEF,
∴AC=DF.
∵∠ACB=∠F,∴AC∥DF.
∴四边形ACFD 是平行四边形.
∴AD∥CF,AD=CF.
∵EC=CF,∴AD=EC.
又∵AD∥EC,
∴四边形AECD 是平行四边形.
解:
课堂小结
课堂小结
A
B
C
D
O
平行四边形的判定方法:如图:
(1)两组对边分别相等的四边形是平行四边形.
几何语言: ∵AB=CD,AD=BC,
∴四边形ABCD 是平行四边形.
(2)对角线互相平分的四边形是平行四边形.
几何语言: ∵AO=CO,BO=DO,
∴四边形ABCD 是平行四边形.
课堂小结
(3)两组对角分别相等的四边形是平行四边形.
几何语言: ∵∠ABC=∠ADC,∠BAD=∠BCD,
∴四边形ABCD 是平行四边形.
注意: ①当四边形的两组对边分别相等时,连接对角线,把四边形分成两个三角形,通过证明三角形全等来证明两组对边平行. ②在已知或易证一组对边相等时,可以考虑证明另一组对边相等或证明这组对边平行. ③需要注意的是“平行且相等”指的是同一组对边,不能是一组对边平行,另一组对变形等. ④从对角线方面判断四边形的形状要注意是对角线互相平分,即交点既是第一条对角线的中点,又是第二条对角线的中点.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.2 平行四边形的判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
根据平行四边形的性质思考:对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?
新课精讲
探索新知
知识点
由两组对边的关系判定平行四边形
如图将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?
1
探索新知
木条在转动过程中,虽然形状发生了变化,但始终是
平行四边形。
由此我们可以猜想:
两组对边分别相等的
四边形是平行四边形。
你能通过几何证明验证你的猜想吗?
B
C
A
D
已知:在四边形ABCD 中, AB=CD,AD=BC.
求证:四边形ABCD 是平行四边形.
证明:连结AC,在△ABC 和△CDA 中
∴△ABC ≌△CDA (SSS)
∴∠1=∠2,∠3=∠4 (全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形. (平行四边形的定义)
探索新知
B
D
A
C
2
1
3
4
通过证明验证了猜想的正确性,因此我们得到平行四
边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
数学语言表示:
∵AB=CD,AD=BC (已知)
∴四边形ABCD 是平行四边形.
(两组对边分别相等的四边形是平行四边形)
探索新知
归 纳
B
D
A
C
探索新知
例1 如图,分别以△ABC 的三边为一边,在BC 的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF 是平行四边形.
导引:由等边三角形的性质可以得到线段相等,角相等,
进而可以通过全等三角形证明四边形ADEF 的两
组对边分别相等,最后根据两组对边分别相等的
四边形是平行四边形进行判定.
探索新知
∵△ABD、△BCE、△ACF 都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC.∴△DBE ≌△ABC.∴DE=AC.
又∵AC=AF,∴AF=DE.
同理可证△ABC ≌△FEC,∴AB=FE.∴FE=AD.
∴四边形ADEF 是平行四边形.
证明:
探索新知
总 结
解答本题时通过证明三角形全等得到四边形ADEF 的两组对边分别相等是关键.
典题精讲
已知:如图, AC 为 ABCD 的对角线,DE⊥AC,BF⊥AC,垂足分别为E,F.
求证:四边形DEBF 是平行四边形
典题精讲
在 ABCD 中,AD∥BC,AD=BC.
因为DE⊥AC,BF⊥AC,
所以∠DEA=∠DEF=∠BFE=∠BFC=90°,
因为AD∥BC,所以∠DAE=∠BCF,
在△ADE 和△CBF 中,
所以△ADE ≌△CBF,
所以DE=BF,因为∠DEF=∠BFE=90°,
所以DE∥BF,所以四边形DEBF 是平行四边形.
证明:
典题精讲
2 如图,已知三点A,B,C.画平行四边形,使其三个顶点分别是A,B,C.
解:略.
典题精讲
3 已知:如图,在 ABCD 的各边AB,BC,CD , DA上分别取点K,L, M,N,使AK=CM,BL=DN. 求证:四边形KLMN 是平行四边形.
典题精讲
在 ABCD 中,∠A=∠C,∠B=∠D,AB=CD,AD=BC,因为AK=CM,所以DM=BK,
在△NDM 和△LBK 中,
所以△NDM ≌△LBK.
所以MN=KL,
同理可得NK=ML,
所以四边形KLMN 是平行四边形.
证明:
典题精讲
四边形的四条边长分别是a,b,c,d,其中a,b 为一组对边长,c,d 为另一组对边长且a 2+b 2+c 2+d 2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线互相垂直的四边形
4
B
典题精讲
下列图形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个锐角三角形
D.两个全等三角形
5
D
探索新知
2
知识点
由对角线互相平分判定平行四边形
通过前面的学习,我们知道,平行四边形的对边相
等、对角相等、对角线互相平分.反过来,对边相等,或
对角相等,或对角线互相平分的四边形是平行四边形吗?
也就是说,平行四边形的性质定理的逆命题成立吗?
下面我们以“对角线互相平分的四边形是平行四边
形”为例,通过三角形 全等进行证明.
思考
探索新知
如图,在四边形ABCD 中,AC,BD 相交于点O,
且OA=OC,OB=OD.
求证:四边形ABCD 是平行四边形.
∵OA=OC,OD=OB,
∠AOD=∠COB,
∴△ AOD ≌△COB.
∴∠OAD =∠OCB.
∴AD//BC.
同理 AB//DC.
∴四边形ABCD 是平行四边形.
证明:
A
B
C
D
O
探索新知
归 纳
平行四边形的判定定理3:
两条对角线互相平分的四边形是平行四边形.
符号语言:如图,
在四边形ABCD 中,
∵AO=CO,BO=DO,
∴四边形ABCD 是平行四边形.
探索新知
例2 已知:如图, ABCD 的两条对角线AC,BD 相交于点O,E,F 分别为OA,OC 的中点.
求证:四边形EBFD 是平行四边形.
证明:∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵E,F 分别为OA,OC 的中点.
∴OE=OF.
∴四边形EBFD 是平行四边形.
探索新知
总 结
从对角线方面判断四边形的形状要注意是对角线互相平分,即交点既是第一条对角线的中点,又是第二条对角线的中点.
典题精讲
1 已知:如图, ABCD 的对角线AC,BD 相交于点O,EF 过点O 交AD 于点E,交BC 于点F,G 是OA 的中点,H 是OC 的中点.
求证:四边形EGFH 是平行四边形.
典题精讲
解:在 ABCD 中,AD∥BC,OA=OC,
因为AD∥BC,所以∠EAO=∠FCO,
在△AEO 和△CFO 中,
所以△AEO ≌△CFO,
所以EO=FO,
因为G 是OA 的中点,H 是OC 的中点,
所以OG=OH= OA= OC,
所以四边形EGFH 是平行四边形.
典题精讲
如图,四边形ABCD 的对角线相交于点O,AO=CO,请添加一个条件______________(只添一个即可),使四边形ABCD 是平行四边形.
2
BO=DO
典题精讲
如图,在四边形ABCD 中,对角线AC,BD 相交于点O,下列条件不能判定四边形ABCD 为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
3
C
探索新知
知识点
平行四边形判定方法的综合应用
例3 如图,四边形ABCD 是平行四边形,E,F 为对角线AC 上两点,连接ED,EB,FD,FB.给出以下条件:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
导引:欲证明∠1=∠2,只需证
得四边形BFDE 是平行四边
形或△ABF ≌△CDE 即可.
3
探索新知
选取条件①BE∥DF.
证明:如图,∵BE∥DF,
∴∠BEC=∠DFA.∴∠BEA=∠DFC.
∵四边形ABCD 是平行四边形,∴AB=CD,AB∥CD.
∴∠BAE=∠DCF.
在△ABE 与△CDF 中,
∴△ABE ≌△CDF (AAS).∴BE=DF.
又∵BE∥DF,∴四边形BFDE 是平行四边形.
∴ED∥BF.∴∠1=∠2.
解:
探索新知
选取条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD 是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAF=∠DCE.
在△ABF 与△CDE 中,
∴△ABF ≌△CDE (SAS).∴∠1=∠2.
探索新知
总 结
平行四边形判定方法综合起来有多种,具体选择哪种方法判定要取决于题目中给出的条件,最终目的都是为了简单、方便的判定四边形是平行四边形.
典题精讲
1 已知:如图,在四边形ABCD 中,对角线AC,BD 相交于点O.仅从下列条件中任意选取两项作为已知条件,能够判定四边形ABCD 是平行四边形的有哪些?
①AB∥CD;②BC=AD;
③AB=CD; ④BC∥AD;
⑤OA=OC; ⑥OB=OD.
解:①③,①④,①⑤,①⑥,②③,②④,④⑤,④⑥,⑤⑥均能够判定四边形ABCD 是平行四边形.
典题精讲
2 已知:如图,D,E 分别为△ABC 的边AB 和AC 的中点,延长AE 到点F,使EF=DE,连接CF.
求证:四边形BCFD 是平行四边形.
典题精讲
如图,连接AF,DC.
由点D,E分别为△ABC 的边AB 和边AC 的中点,
得AD=BD,AE=EC,
由AE=CE,DE=EF
可得四边形ADCF 是平行四边形,
所以AD∥CF,AD=CF,
又因为AD=BD,所以BD=CF,
又因为BD∥CF,所以四边形BCFD 是平行四边形.
证明:
典题精讲
3 如图,在 ABCD 中,E 为BC 边上一点.试在AD 边上找一点F,使四边形AECF 是平行四边形,并说明理由.
解:在AD 边上找一点F,当满足AF=EC 时,可使得四边形AECF 是平行四边形.说明理由略.
A
B
C
D
E
典题精讲
下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
4
D
易错提醒
如图,在 ABCD 中,对角线AC,BD 相交于O,E,F是对角线上的两点,给出下列4个条件:
①OE=OF; ②DE=BF;
③∠ADE=∠CBF;
④∠ABE=∠CDF.
其中不能判定四边形DEBF 是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个
易错点:混淆平行四边形的判定方法致判断错误.
B
学以致用
小试牛刀
在四边形ABCD 中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD 中任选两个使四边形ABCD 为平行四边形的选法有( )
A.3种 B.4种
C.5种 D.6种
1
B
小试牛刀
如图,在四边形ABCD 中,对角线AC,BD 相交于E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD 的面积为( )
A.6 B.12
C.20 D.24
2
D
小试牛刀
在四边形ABCD 中,对角线AC,BD 相交于点O,给出下列4组条件:
①AB∥CD,AD∥BC;②AB=CD,AD=BC;
③AO=CO,BO=DO;④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组 B.2组
C.3组 D.4组
3
C
小试牛刀
4
如图,在△ABC 中,∠ABC=90°,∠BAC=60°,△ACD 是等边三角形,E 是AC 的中点,连接BE 并延长,交DC 于点F,求证:
(1)△ABE ≌△CFE;
(2)四边形ABFD 是平行四边形.
小试牛刀
(1)∵△ACD 是等边三角形,
∴∠DCA=60°.
又∵∠BAC=60°,
∴∠DCA=∠BAC.
∵E 是AC 的中点,
∴AE=CE.
在△ABE 与△CFE 中,
∴△ABE ≌△CFE.
证明:
小试牛刀
(2)∵E 是AC 的中点,∴AE= AC.
在Rt△ABC 中,∠ABC=90°,∠BAC=60°,
∴∠ACB=30°,∴AB= AC.
∴AB=AE.
∴△ABE 是等边三角形.
∴△CFE 是等边三角形.
∴∠CFE=60°.
解:
小试牛刀
∵△ACD 是等边三角形,
∴∠CDA=60°.
∴∠CFE=∠CDA.
∴BF∥AD.
又由(1)知∠DCA=∠BAC,
∴AB∥CD.
∴四边形ABFD 是平行四边形.
小试牛刀
如图,在 ABCD 中,点E,F 在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF 是平行四边形.
5
小试牛刀
(1)∵四边形ABCD 是平行四边形.
∴AD∥CB,AD=CB.∴∠DAE=∠BCF.
在△ADE 和△CBF 中,
∴△ADE ≌△CBF. ∴DE=BF.
(2)如图,连接BD,交AC 于点O,
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OE=OF.
∴四边形DEBF 是平行四边形.
证明:
小试牛刀
6
已知:如图,E,F 分别为 ABCD 中AD,BC 的中点,连接AF,BE 交于点G,连接CE,DF 交于点H.
求证:EF 与GH 互相平分.
小试牛刀
∵E 为AD 的中点,F 为BC 的中点,
∴AE= AD,CF= BC.
∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC.
∴AE∥CF,AE=CF.
∴四边形AFCE 是平行四边形.
∴AF∥CE. 同理可证BE∥DF.
∴四边形GFHE 是平行四边形.
∴EF 与GH 互相平分.
证明:
小试牛刀
7
如图,已知点E,C 在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC ≌△DEF;
(2)试判断四边形AECD 的形状,并证明你的结论.
小试牛刀
(1) ∵AB∥DE,
∴∠B=∠DEF.
∵BE=EC=CF,∴BC=EF.
在△ABC 和△DEF 中,
∴△ABC ≌△DEF.
证明:
小试牛刀
(2) 四边形AECD 是平行四边形.
证明:∵△ABC ≌△DEF,
∴AC=DF.
∵∠ACB=∠F,∴AC∥DF.
∴四边形ACFD 是平行四边形.
∴AD∥CF,AD=CF.
∵EC=CF,∴AD=EC.
又∵AD∥EC,
∴四边形AECD 是平行四边形.
解:
课堂小结
课堂小结
A
B
C
D
O
平行四边形的判定方法:如图:
(1)两组对边分别相等的四边形是平行四边形.
几何语言: ∵AB=CD,AD=BC,
∴四边形ABCD 是平行四边形.
(2)对角线互相平分的四边形是平行四边形.
几何语言: ∵AO=CO,BO=DO,
∴四边形ABCD 是平行四边形.
课堂小结
(3)两组对角分别相等的四边形是平行四边形.
几何语言: ∵∠ABC=∠ADC,∠BAD=∠BCD,
∴四边形ABCD 是平行四边形.
注意: ①当四边形的两组对边分别相等时,连接对角线,把四边形分成两个三角形,通过证明三角形全等来证明两组对边平行. ②在已知或易证一组对边相等时,可以考虑证明另一组对边相等或证明这组对边平行. ③需要注意的是“平行且相等”指的是同一组对边,不能是一组对边平行,另一组对变形等. ④从对角线方面判断四边形的形状要注意是对角线互相平分,即交点既是第一条对角线的中点,又是第二条对角线的中点.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
