【班海精品】冀教版(新)八下-22.2 平行四边形的判定 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-22.2 平行四边形的判定 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览









文档简介
(共59张PPT)
22.2 平行四边形的判定
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
一装潢店要招聘店员,老板出了这样一道考题:
“一顾客要一张平行四边形的玻璃,你利用工具度
量哪些数据可说明这张玻璃符合顾客要求.”
如何说明右图是平行四边形?
新课精讲
探索新知
1
知识点
由两组对边分别平行判定平行四边形
平行四边形的定义既是它的一个性质,又是它的一种
判定方法:
∵四边形ABCD 是平行四边形,∴
反过来, ∵ ∴四边形ABCD 是平行四边形.
AB∥CD
AD∥BC
AB∥CD
AD∥BC
探索新知
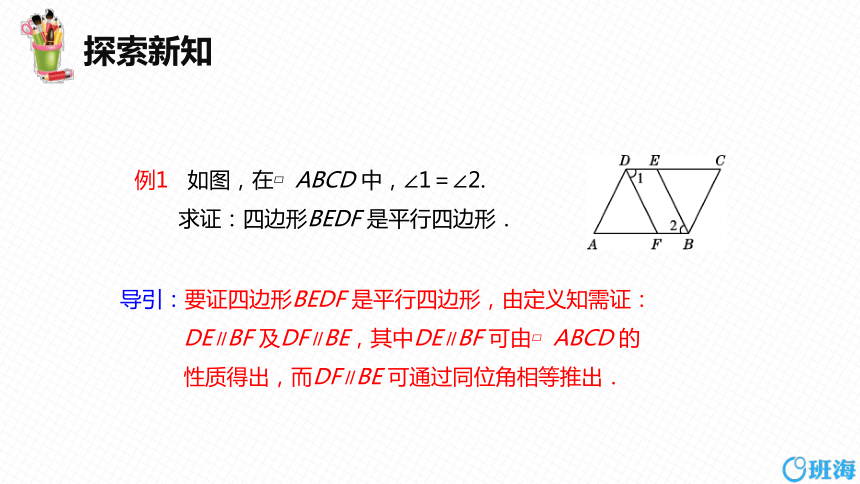
例1 如图,在 ABCD 中,∠1=∠2.
求证:四边形BEDF 是平行四边形.
导引:要证四边形BEDF 是平行四边形,由定义知需证:
DE∥BF 及DF∥BE,其中DE∥BF 可由 ABCD 的
性质得出,而DF∥BE 可通过同位角相等推出.
探索新知
证明: ∵四边形ABCD 是平行四边形,
∴CD∥AB (平行四边形的两组对边分别平行),
∴DE∥BF,∴∠1=∠DFA.
又∵∠1=∠2,∴∠2=∠DFA,∴DF∥BE,
∴四边形BEDF 是平行四边形(两组对边分别平
行的四边形是平行四边形).
探索新知
总 结
当题目的条件中有平行四边形时,应立即想到两
组对边分别平行;当题目中有要证的平行四边形时,
首先应联想到它的两组对边是否分别平行.平行四边
形的定义的逆向利用及正向利用是后面学习平行四边
形的性质及判定的主要依据.
典题精讲
1 两组对角分别相等的四边形是平行四边形吗?为什么?
解:是;说明理由略.
典题精讲
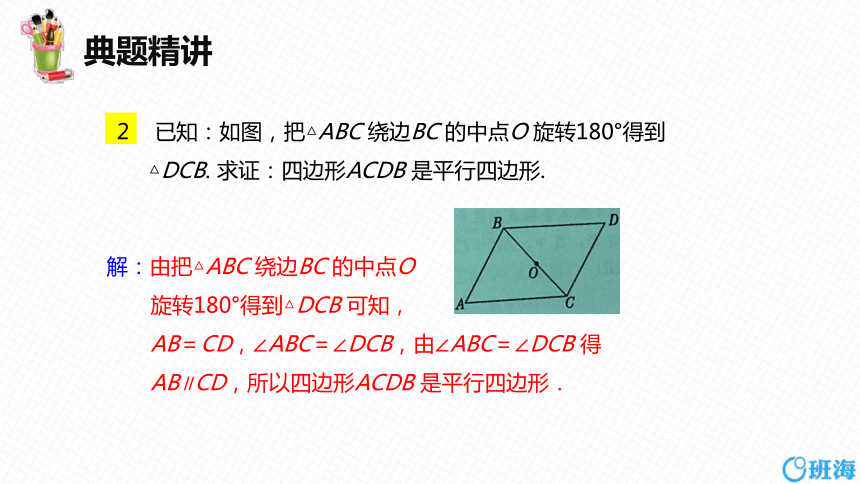
2 已知:如图,把△ABC 绕边BC 的中点O 旋转180°得到△DCB. 求证:四边形ACDB 是平行四边形.
解:由把△ABC 绕边BC 的中点O
旋转180°得到△DCB 可知,
AB=CD,∠ABC=∠DCB,由∠ABC=∠DCB 得AB∥CD,所以四边形ACDB 是平行四边形.
典题精讲
下列条件不能判定四边形ABCD 是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
3
D
典题精讲
小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①②
B.①④
C.③④
D.②③
4
D
探索新知
2
知识点
由一组对边平行且相等判定平行四边形
小明用下列方法得到一个四边形ABCD.
画两条互相平行的直线,在这两条直线上分别截取线段AB=CD,连接AD,BC,得四边形ABCD.
探索新知
(1)将线段AB 沿BC 方向平行移动,线段AB 与CD 能不能重合?你认为这样得到的四边形ABCD 是不是平行四边形?
(2)由此,你发现了什么结果?与大家交流.
我们发现:一组对边平行且相等的四边形是平行四边形.
现在,我们来证明这个结论.
已知:如图,在四边形ABCD 中,AD∥BC,AD =BC.
求证:四边形ABCD 是平行四边形.
探索新知
如图,连接BD.
在△ABD 和△CDB 中,
∵AD∥BC,∴∠ADB=∠CBD.
∵AD=CB,BD=DB,∴△ABD ≌△CDB.
∴∠ABD =∠CDB. ∴AB∥DC.
∴四边形ABCD 是平行四边形.
证明:
探索新知
归 纳
一组对边平行且相等的四边形是平行四边形.
探索新知
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形.
符号语言:如图,在四边形ABCD 中,
∵AB∥CD,AB=CD,
∴四边形ABCD 是平行四边形.
探索新知
例2 已知:如图,在 ABCD 中,E 为BA 延长线上一点,F 为DC 延长线上一点,且AE=CF,连接 BF,DE.
求证:四边形BFDE 是平行四边形.
探索新知
证明: ∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD.
又∵AE=CF,
∴BE=BE+AE=DC+CF=DF.
且BE∥DF.
∴四边形BFDE 是平行四边形.
探索新知
总 结
当已知条件中有一组对边平行时,常常利用三角
形全等证明这组对边相等或利用平行线的判定证明另
一组对边平行,从而判定这个四边形是平行四边形.
典题精讲
1 将两块全等的含30°角的三角尺按如图的方式摆放在一起,则四边形ABCD 是平行四边形吗?请尝试用多种方法说明理由.
解:是;说明理由略.
典题精讲
2 如图,在 ABCD 中,延长AB 到点E,延长CD 到点F,使BE=DF. 猜想线段AC 与EF 之间的关系,并证明自己的猜想.
典题精讲
AC 与EF 互相平分;
证明如下:如图,连接AF,CE.
在 ABCD 中,AB=CD,AB∥CD,
因为BE=DF,所以AE=CF,
又因为AE∥CF,
所以四边形AECF 是平行四边形,所以AC 与EF 互相平分.
解:
典题精讲
3 已知:如图,BD 是 ABCD 的对角线,点E 和点F 在BD上,且BE=DF.求证:四边形AECF 是平行四边形.
典题精讲
在 ABCD 中,AB=CD,AB∥CD,
因为AB∥CD,所以∠ABE=∠CDF,
在△ABE 和△CDF 中,
所以△ABE ≌△CDF,
所以AE=FC,∠AEB=∠CFD,
由∠AEB=∠CFD 得∠AEF=∠CFE,
所以AE∥CF,
由AE=FC,AE∥FC 得四边形AECF 是平行四边形.
证明:
典题精讲
已知:如图,△ABC 是等边三角形,点D,F 分别在
线段BC,AB上,DC=EF,∠EFB=60°.
求证:四边形EDCF 是平行四边形.
典题精讲
证明:在等边三角形ABC 中,∠B=60°,
因为∠EFB=60°=∠B,
所以EF∥DC,
又因为EF=DC,
所以四边形EDCF 是平行四边形.
典题精讲
5 已知:如图,在四边形ABCD 中,AD∥BC,AE⊥AD,交BD 于点E,CF⊥BC,交BD 于点F,且AE=CF.
求证:四边形ABCD 是平行四边形.
典题精讲
因为AE⊥AD,CF⊥BC,
所以∠EAD=∠FCB=90°,
因为AD∥BC,所以∠ADE=∠CBF,
在△ADE 和△CBF 中,
所以△ADE ≌△CBF,
所以AD=CB,
又因为AD∥BC,
所以四边形ABCD 是平行四边形.
证明:
典题精讲
下列条件中,不能判定四边形是平行四边形的是( )
A.两组对边分别平行
B.一组对边平行,另一组对边相等
C.在四边形ABCD 中,AB=CD,AB∥CD
D.两组对角分别相等
6
B
典题精讲
如图,在 ABCD 中,E,F 分别是AB,CD 的中点,连接DE,EF,BF,则图中平行四边形共有( )
A.2个
B.4个
C.6个
D.8个
7
B
典题精讲
在四边形ABCD 中,AD=BC,若四边形ABCD 是平行四边形,则还应满足( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°
8
C
探索新知
3
知识点
平行线之间的距离
距离是几何中的重要度量之一.前面我们已经学习
了点与点之间的距离、点到直线的距离.在此基础上,
我们结合平行四边形的概念和性质,介绍两条平行线
之间的距离.
探索新知
如图,a∥b,c∥d,c,d 与a,b 分别相交于A,
B,C,D 四点. 由平行四边形的概念和性质可知,四
边形ABDC 是平行四边形,AB=CD. 也就是说,两条
平行线之间的任何两条平行线段都相等.
A
B
C
D
a
b
c
d
探索新知
归 纳
从上面的结论可以知道,如果两条直线平行,
那么一条直线上所有的点到另一条直线的距离都相
等.两条平行线中,一条直线上任意一点到另一条直
线的距离,叫做这两条平行线之间的距离.如图,A
是a上的任意一点,AB丄b,B 是垂足,线段AB 的长就是a,b 之间的距离.
探索新知
定义:两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
要点精析
(1)点到直线的距离是指直线外一点到这条直线的垂线段的长度;
(2)三种距离之间的区别与联系如下表:
类别 两点间的距离 点到直线的距离 两条平行线间的距离
区别 连接两点的线段的长度 直线外一点到直线的垂线段的长度 两条平行线中,一条直线上的任意一点到另一条直线的垂线段的长度
联系 最后都归结为两点间的线段的长度 探索新知
已知:如图,EF∥MN,A,B 为直线EF上任意两点,
AD丄MN,垂足为D,BC丄MN,垂足为C.
求证:AD=BC.
证明:∵ AD丄MN,BC丄MN,
∴AD∥BC.
又∵EF∥MN,∴四边形ADCB 为平行四边形.
∴AD =BC.
例4 求证:平行线间的距离处处相等.
探索新知
总 结
误区1:“距离”是一条线段的长度,而不是一条线段;
误区2:“两点之间的距离”不需要垂直,而另外两个距离都需要垂直.
典题精讲
直线a上有一点A,直线b上有一点B,且a∥b.点P 在直线a,b 之间,若PA=3,PB=4,则直线a,b 之间的距离( )
A.等于7 B.小于7
C.不小于7 D.不大于7
1
D
典题精讲
如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G 为垂足,则下列说法不正确的是( )
A.AB=CD
B.EC=FG
C.A,B 两点间的距离
就是线段AB 的长度
D.a 与b 之间的距离就是线段CD 的长度
2
D
易错提醒
判断符合下列条件的四边形ABCD 是否是平行四边形.
(1)AB∥CD,∠A=∠C;
(2)AB∥CD,BC=AD.
(1)是.∵AB∥CD,∴∠A+∠D=180°.
又∵∠A=∠C,∴∠C+∠D=180°.∴AD∥BC.
∴四边形ABCD 为平行四边形.
(2)不是.反例:如图所示,
该四边形是等腰梯形,而不是平行四边形.
解:
学以致用
小试牛刀
如图,在梯形ABCD 中,AD∥BC,DE∥AB. 若DE=DC,∠C=80°,则∠A=( )
A.80°
B.90°
C.100°
D.110°
1
C
小试牛刀
如图,在 ABCD 中,点E,F 分别在AD,BC上,若要使四边形AFCE 是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;
③BF=DE;④AF∥CE
A.①或② B.②或③
C.③或④ D.①或③
2
C
小试牛刀
如图,a∥b,若要使S△ABC=S△DEF,需增加条件( )
A.AB=DE
B.AC=DF
C.BC=EF
D.BE=AD
3
C
小试牛刀
4
如图,已知BD 是△ABC 的角平分线,点E,F 分别在边AB,BC 上,ED∥BC,EF∥AC. 求证:EB=CF.
小试牛刀
∵ED∥BC,EF∥AC.
∴四边形EFCD 是平行四边形,
∴DE=CF.
∵BD 平分∠ABC,
∴∠EBD=∠DBC.
∵DE∥BC,∴∠EDB=∠DBC,
∴∠EBD=∠EDB,∴EB=ED,
∴EB=CF.
证明:
小试牛刀
5
如图,在平行四边形ABCD 中,∠C=60°,M,N 分别是AD,BC 的中点,BC=2CD.
求证:
(1)四边形MNCD 是平行四边形;
(2)BD= MN.
小试牛刀
(1)∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC.
∵M,N 分别是AD,BC 的中点,
∴MD=NC,MD∥NC,
∴四边形MNCD 是平行四边形.
证明:
小试牛刀
(2)如图,连接DN.
∵N 是BC 的中点,BC=2CD,∴CD=NC.
又∵∠C=60°,
∴△DCN 是等边三角形.
∴ND=NC,∠DNC=∠NDC=60°.
∴ND=NB=CN. 易得∠DBC=∠BDN=30°.
∴∠BDC=∠BDN+∠NDC=90°.
∴BD=
∵四边形MNCD 是平行四边形,
∴MN=CD. ∴BD= MN.
证明:
小试牛刀
6
如图,以BC 为底边的等腰△ABC,点D,E,G 分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE 至点F,使得BF=BE.
(1)求证:四边形BDEF 为平行四边形;
(2)当∠C=45°,BD=2时,求D,F 两点间的距离.
小试牛刀
(1) ∵△ABC 是等腰三角形,
∴∠ABC=∠C.
∵EG∥BC,DE∥AC,
∴∠AEG=∠ABC=∠C,
四边形CDEG 是平行四边形.
∴∠DEG=∠C.
∵BE=BF,
∴∠BEF=∠F=∠AEG=∠ABC.
∴∠F=∠DEG. ∴BF∥DE.
∴四边形BDEF 为平行四边形.
证明:
小试牛刀
(2)∵∠C=45°,
∴∠BDE=∠ABC=∠BEF=∠BFE=45°.
∴△BDE、△BEF 是等腰直角三角形.
∵BD=2,∴BF=BE= .
作FM⊥BD 交DB 的延长线于M,连接DF,
如图所示.
易得△BFM 是等腰直角三角形,
∴FM=BM=1. ∴DM=3.
在Rt△DFM 中,
由勾股定理得DF= ,
即D,F 两点间的距离为 .
解:
小试牛刀
7
如图,在四边形ABCD 中,AD∥BC,且AD>BC,BC=6 cm. 动点P,Q 分别从点A,C 同时出发,点P 以1 cm/s的速度由点A 向点D 运动,点Q 以2 cm/s的速度由点C 向点B 运动.几秒后,四边形ABQP 是平行四边形?
小试牛刀
设x s后,四边形ABQP 是平行四边形,
则AP=x,CQ=2x,
∴BQ=6-2x.
∵AD∥BC,
∴当AP=BQ 时,四边形ABQP 是平行四边形.
∴x=6-2x. 解得x=2.
∴2 s后,四边形ABQP 是平行四边形.
解:
课堂小结
课堂小结
平行四边形的判定方法:如图:
(1)定义:两组对边分别平行的四边形是平行四边形.
几何语言:∵AB∥CD,AD∥BC,
∴四边形ABCD 是平行四边形.
(2)一组对边平行且相等的四边形是平行四边形.
几何语言(如图):
∵AB∥CD,AB=CD,
∴四边形ABCD 是平行四边形.
A
B
C
D
A
B
C
D
O
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.2 平行四边形的判定
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
一装潢店要招聘店员,老板出了这样一道考题:
“一顾客要一张平行四边形的玻璃,你利用工具度
量哪些数据可说明这张玻璃符合顾客要求.”
如何说明右图是平行四边形?
新课精讲
探索新知
1
知识点
由两组对边分别平行判定平行四边形
平行四边形的定义既是它的一个性质,又是它的一种
判定方法:
∵四边形ABCD 是平行四边形,∴
反过来, ∵ ∴四边形ABCD 是平行四边形.
AB∥CD
AD∥BC
AB∥CD
AD∥BC
探索新知
例1 如图,在 ABCD 中,∠1=∠2.
求证:四边形BEDF 是平行四边形.
导引:要证四边形BEDF 是平行四边形,由定义知需证:
DE∥BF 及DF∥BE,其中DE∥BF 可由 ABCD 的
性质得出,而DF∥BE 可通过同位角相等推出.
探索新知
证明: ∵四边形ABCD 是平行四边形,
∴CD∥AB (平行四边形的两组对边分别平行),
∴DE∥BF,∴∠1=∠DFA.
又∵∠1=∠2,∴∠2=∠DFA,∴DF∥BE,
∴四边形BEDF 是平行四边形(两组对边分别平
行的四边形是平行四边形).
探索新知
总 结
当题目的条件中有平行四边形时,应立即想到两
组对边分别平行;当题目中有要证的平行四边形时,
首先应联想到它的两组对边是否分别平行.平行四边
形的定义的逆向利用及正向利用是后面学习平行四边
形的性质及判定的主要依据.
典题精讲
1 两组对角分别相等的四边形是平行四边形吗?为什么?
解:是;说明理由略.
典题精讲
2 已知:如图,把△ABC 绕边BC 的中点O 旋转180°得到△DCB. 求证:四边形ACDB 是平行四边形.
解:由把△ABC 绕边BC 的中点O
旋转180°得到△DCB 可知,
AB=CD,∠ABC=∠DCB,由∠ABC=∠DCB 得AB∥CD,所以四边形ACDB 是平行四边形.
典题精讲
下列条件不能判定四边形ABCD 是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
3
D
典题精讲
小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①②
B.①④
C.③④
D.②③
4
D
探索新知
2
知识点
由一组对边平行且相等判定平行四边形
小明用下列方法得到一个四边形ABCD.
画两条互相平行的直线,在这两条直线上分别截取线段AB=CD,连接AD,BC,得四边形ABCD.
探索新知
(1)将线段AB 沿BC 方向平行移动,线段AB 与CD 能不能重合?你认为这样得到的四边形ABCD 是不是平行四边形?
(2)由此,你发现了什么结果?与大家交流.
我们发现:一组对边平行且相等的四边形是平行四边形.
现在,我们来证明这个结论.
已知:如图,在四边形ABCD 中,AD∥BC,AD =BC.
求证:四边形ABCD 是平行四边形.
探索新知
如图,连接BD.
在△ABD 和△CDB 中,
∵AD∥BC,∴∠ADB=∠CBD.
∵AD=CB,BD=DB,∴△ABD ≌△CDB.
∴∠ABD =∠CDB. ∴AB∥DC.
∴四边形ABCD 是平行四边形.
证明:
探索新知
归 纳
一组对边平行且相等的四边形是平行四边形.
探索新知
平行四边形的判定定理1:
一组对边平行且相等的四边形是平行四边形.
符号语言:如图,在四边形ABCD 中,
∵AB∥CD,AB=CD,
∴四边形ABCD 是平行四边形.
探索新知
例2 已知:如图,在 ABCD 中,E 为BA 延长线上一点,F 为DC 延长线上一点,且AE=CF,连接 BF,DE.
求证:四边形BFDE 是平行四边形.
探索新知
证明: ∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD.
又∵AE=CF,
∴BE=BE+AE=DC+CF=DF.
且BE∥DF.
∴四边形BFDE 是平行四边形.
探索新知
总 结
当已知条件中有一组对边平行时,常常利用三角
形全等证明这组对边相等或利用平行线的判定证明另
一组对边平行,从而判定这个四边形是平行四边形.
典题精讲
1 将两块全等的含30°角的三角尺按如图的方式摆放在一起,则四边形ABCD 是平行四边形吗?请尝试用多种方法说明理由.
解:是;说明理由略.
典题精讲
2 如图,在 ABCD 中,延长AB 到点E,延长CD 到点F,使BE=DF. 猜想线段AC 与EF 之间的关系,并证明自己的猜想.
典题精讲
AC 与EF 互相平分;
证明如下:如图,连接AF,CE.
在 ABCD 中,AB=CD,AB∥CD,
因为BE=DF,所以AE=CF,
又因为AE∥CF,
所以四边形AECF 是平行四边形,所以AC 与EF 互相平分.
解:
典题精讲
3 已知:如图,BD 是 ABCD 的对角线,点E 和点F 在BD上,且BE=DF.求证:四边形AECF 是平行四边形.
典题精讲
在 ABCD 中,AB=CD,AB∥CD,
因为AB∥CD,所以∠ABE=∠CDF,
在△ABE 和△CDF 中,
所以△ABE ≌△CDF,
所以AE=FC,∠AEB=∠CFD,
由∠AEB=∠CFD 得∠AEF=∠CFE,
所以AE∥CF,
由AE=FC,AE∥FC 得四边形AECF 是平行四边形.
证明:
典题精讲
已知:如图,△ABC 是等边三角形,点D,F 分别在
线段BC,AB上,DC=EF,∠EFB=60°.
求证:四边形EDCF 是平行四边形.
典题精讲
证明:在等边三角形ABC 中,∠B=60°,
因为∠EFB=60°=∠B,
所以EF∥DC,
又因为EF=DC,
所以四边形EDCF 是平行四边形.
典题精讲
5 已知:如图,在四边形ABCD 中,AD∥BC,AE⊥AD,交BD 于点E,CF⊥BC,交BD 于点F,且AE=CF.
求证:四边形ABCD 是平行四边形.
典题精讲
因为AE⊥AD,CF⊥BC,
所以∠EAD=∠FCB=90°,
因为AD∥BC,所以∠ADE=∠CBF,
在△ADE 和△CBF 中,
所以△ADE ≌△CBF,
所以AD=CB,
又因为AD∥BC,
所以四边形ABCD 是平行四边形.
证明:
典题精讲
下列条件中,不能判定四边形是平行四边形的是( )
A.两组对边分别平行
B.一组对边平行,另一组对边相等
C.在四边形ABCD 中,AB=CD,AB∥CD
D.两组对角分别相等
6
B
典题精讲
如图,在 ABCD 中,E,F 分别是AB,CD 的中点,连接DE,EF,BF,则图中平行四边形共有( )
A.2个
B.4个
C.6个
D.8个
7
B
典题精讲
在四边形ABCD 中,AD=BC,若四边形ABCD 是平行四边形,则还应满足( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°
8
C
探索新知
3
知识点
平行线之间的距离
距离是几何中的重要度量之一.前面我们已经学习
了点与点之间的距离、点到直线的距离.在此基础上,
我们结合平行四边形的概念和性质,介绍两条平行线
之间的距离.
探索新知
如图,a∥b,c∥d,c,d 与a,b 分别相交于A,
B,C,D 四点. 由平行四边形的概念和性质可知,四
边形ABDC 是平行四边形,AB=CD. 也就是说,两条
平行线之间的任何两条平行线段都相等.
A
B
C
D
a
b
c
d
探索新知
归 纳
从上面的结论可以知道,如果两条直线平行,
那么一条直线上所有的点到另一条直线的距离都相
等.两条平行线中,一条直线上任意一点到另一条直
线的距离,叫做这两条平行线之间的距离.如图,A
是a上的任意一点,AB丄b,B 是垂足,线段AB 的长就是a,b 之间的距离.
探索新知
定义:两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
要点精析
(1)点到直线的距离是指直线外一点到这条直线的垂线段的长度;
(2)三种距离之间的区别与联系如下表:
类别 两点间的距离 点到直线的距离 两条平行线间的距离
区别 连接两点的线段的长度 直线外一点到直线的垂线段的长度 两条平行线中,一条直线上的任意一点到另一条直线的垂线段的长度
联系 最后都归结为两点间的线段的长度 探索新知
已知:如图,EF∥MN,A,B 为直线EF上任意两点,
AD丄MN,垂足为D,BC丄MN,垂足为C.
求证:AD=BC.
证明:∵ AD丄MN,BC丄MN,
∴AD∥BC.
又∵EF∥MN,∴四边形ADCB 为平行四边形.
∴AD =BC.
例4 求证:平行线间的距离处处相等.
探索新知
总 结
误区1:“距离”是一条线段的长度,而不是一条线段;
误区2:“两点之间的距离”不需要垂直,而另外两个距离都需要垂直.
典题精讲
直线a上有一点A,直线b上有一点B,且a∥b.点P 在直线a,b 之间,若PA=3,PB=4,则直线a,b 之间的距离( )
A.等于7 B.小于7
C.不小于7 D.不大于7
1
D
典题精讲
如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G 为垂足,则下列说法不正确的是( )
A.AB=CD
B.EC=FG
C.A,B 两点间的距离
就是线段AB 的长度
D.a 与b 之间的距离就是线段CD 的长度
2
D
易错提醒
判断符合下列条件的四边形ABCD 是否是平行四边形.
(1)AB∥CD,∠A=∠C;
(2)AB∥CD,BC=AD.
(1)是.∵AB∥CD,∴∠A+∠D=180°.
又∵∠A=∠C,∴∠C+∠D=180°.∴AD∥BC.
∴四边形ABCD 为平行四边形.
(2)不是.反例:如图所示,
该四边形是等腰梯形,而不是平行四边形.
解:
学以致用
小试牛刀
如图,在梯形ABCD 中,AD∥BC,DE∥AB. 若DE=DC,∠C=80°,则∠A=( )
A.80°
B.90°
C.100°
D.110°
1
C
小试牛刀
如图,在 ABCD 中,点E,F 分别在AD,BC上,若要使四边形AFCE 是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;
③BF=DE;④AF∥CE
A.①或② B.②或③
C.③或④ D.①或③
2
C
小试牛刀
如图,a∥b,若要使S△ABC=S△DEF,需增加条件( )
A.AB=DE
B.AC=DF
C.BC=EF
D.BE=AD
3
C
小试牛刀
4
如图,已知BD 是△ABC 的角平分线,点E,F 分别在边AB,BC 上,ED∥BC,EF∥AC. 求证:EB=CF.
小试牛刀
∵ED∥BC,EF∥AC.
∴四边形EFCD 是平行四边形,
∴DE=CF.
∵BD 平分∠ABC,
∴∠EBD=∠DBC.
∵DE∥BC,∴∠EDB=∠DBC,
∴∠EBD=∠EDB,∴EB=ED,
∴EB=CF.
证明:
小试牛刀
5
如图,在平行四边形ABCD 中,∠C=60°,M,N 分别是AD,BC 的中点,BC=2CD.
求证:
(1)四边形MNCD 是平行四边形;
(2)BD= MN.
小试牛刀
(1)∵四边形ABCD 是平行四边形,
∴AD∥BC,AD=BC.
∵M,N 分别是AD,BC 的中点,
∴MD=NC,MD∥NC,
∴四边形MNCD 是平行四边形.
证明:
小试牛刀
(2)如图,连接DN.
∵N 是BC 的中点,BC=2CD,∴CD=NC.
又∵∠C=60°,
∴△DCN 是等边三角形.
∴ND=NC,∠DNC=∠NDC=60°.
∴ND=NB=CN. 易得∠DBC=∠BDN=30°.
∴∠BDC=∠BDN+∠NDC=90°.
∴BD=
∵四边形MNCD 是平行四边形,
∴MN=CD. ∴BD= MN.
证明:
小试牛刀
6
如图,以BC 为底边的等腰△ABC,点D,E,G 分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE 至点F,使得BF=BE.
(1)求证:四边形BDEF 为平行四边形;
(2)当∠C=45°,BD=2时,求D,F 两点间的距离.
小试牛刀
(1) ∵△ABC 是等腰三角形,
∴∠ABC=∠C.
∵EG∥BC,DE∥AC,
∴∠AEG=∠ABC=∠C,
四边形CDEG 是平行四边形.
∴∠DEG=∠C.
∵BE=BF,
∴∠BEF=∠F=∠AEG=∠ABC.
∴∠F=∠DEG. ∴BF∥DE.
∴四边形BDEF 为平行四边形.
证明:
小试牛刀
(2)∵∠C=45°,
∴∠BDE=∠ABC=∠BEF=∠BFE=45°.
∴△BDE、△BEF 是等腰直角三角形.
∵BD=2,∴BF=BE= .
作FM⊥BD 交DB 的延长线于M,连接DF,
如图所示.
易得△BFM 是等腰直角三角形,
∴FM=BM=1. ∴DM=3.
在Rt△DFM 中,
由勾股定理得DF= ,
即D,F 两点间的距离为 .
解:
小试牛刀
7
如图,在四边形ABCD 中,AD∥BC,且AD>BC,BC=6 cm. 动点P,Q 分别从点A,C 同时出发,点P 以1 cm/s的速度由点A 向点D 运动,点Q 以2 cm/s的速度由点C 向点B 运动.几秒后,四边形ABQP 是平行四边形?
小试牛刀
设x s后,四边形ABQP 是平行四边形,
则AP=x,CQ=2x,
∴BQ=6-2x.
∵AD∥BC,
∴当AP=BQ 时,四边形ABQP 是平行四边形.
∴x=6-2x. 解得x=2.
∴2 s后,四边形ABQP 是平行四边形.
解:
课堂小结
课堂小结
平行四边形的判定方法:如图:
(1)定义:两组对边分别平行的四边形是平行四边形.
几何语言:∵AB∥CD,AD∥BC,
∴四边形ABCD 是平行四边形.
(2)一组对边平行且相等的四边形是平行四边形.
几何语言(如图):
∵AB∥CD,AB=CD,
∴四边形ABCD 是平行四边形.
A
B
C
D
A
B
C
D
O
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
