【班海精品】冀教版(新)八下-22.4 矩形 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-22.4 矩形 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览







文档简介
(共60张PPT)
22.4 矩 形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
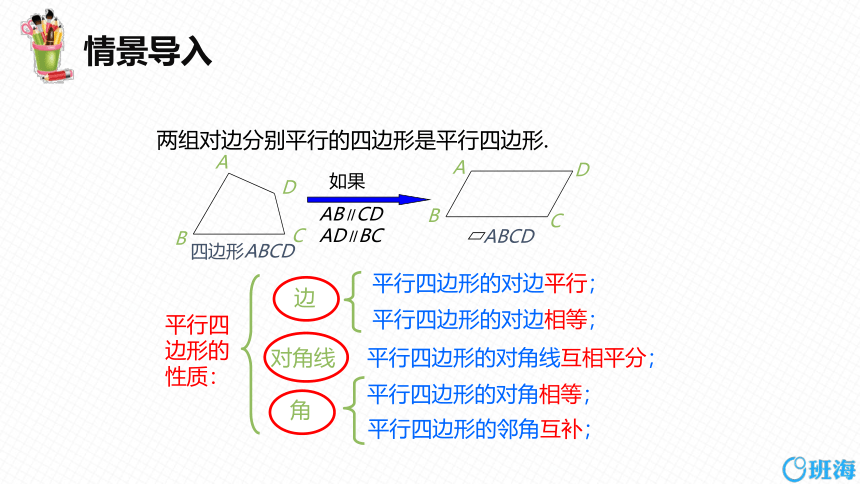
两组对边分别平行的四边形是平行四边形.
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
情景导入
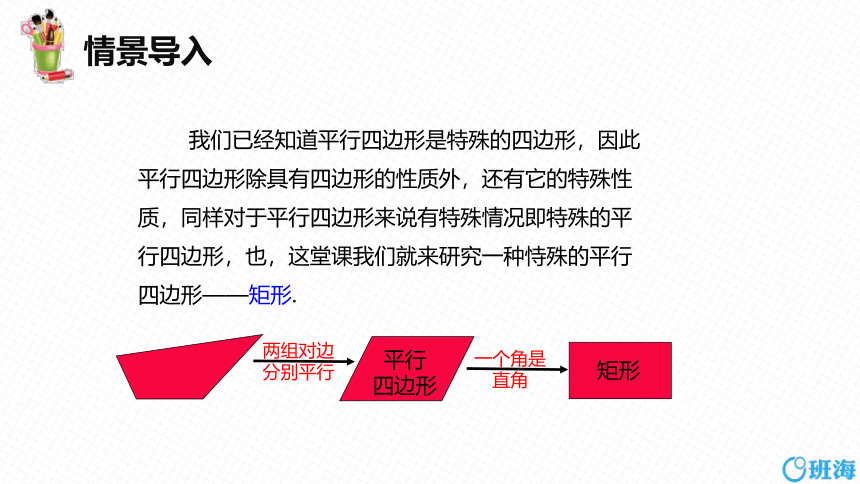
我们已经知道平行四边形是特殊的四边形,因此
平行四边形除具有四边形的性质外,还有它的特殊性
质,同样对于平行四边形来说有特殊情况即特殊的平
行四边形,也,这堂课我们就来研究一种恃殊的平行
四边形——矩形.
一个角是
直角
两组对边
分别平行
平行
四边形
矩形
新课精讲
探索新知
知识点
矩形及其对称性
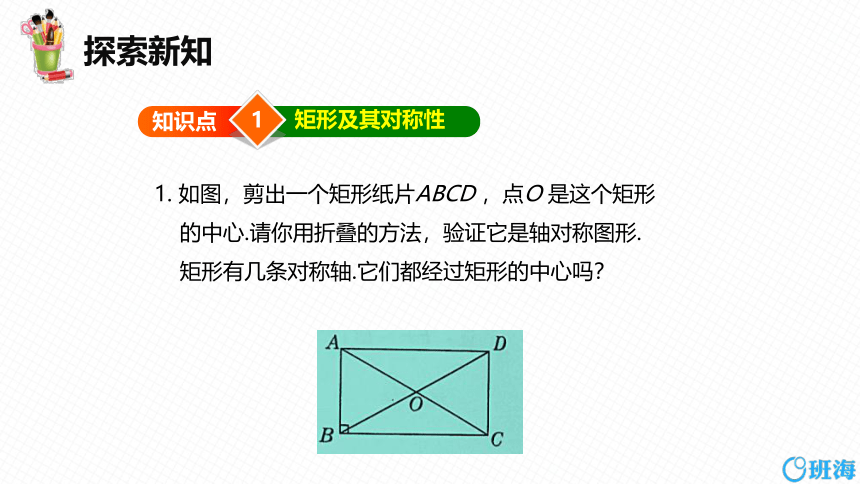
1. 如图,剪出一个矩形纸片ABCD ,点O 是这个矩形
的中心.请你用折叠的方法,验证它是轴对称图形.
矩形有几条对称轴.它们都经过矩形的中心吗?
1
探索新知
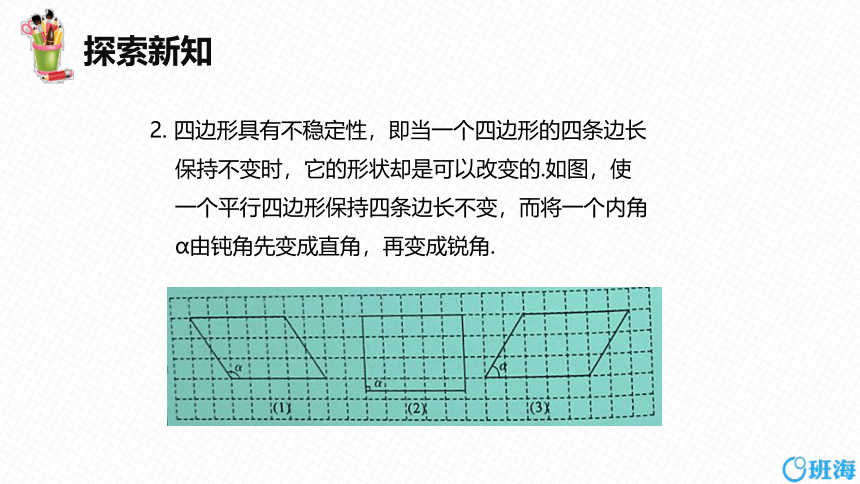
2. 四边形具有不稳定性,即当一个四边形的四条边长
保持不变时,它的形状却是可以改变的.如图,使
一个平行四边形保持四条边长不变,而将一个内角
α由钝角先变成直角,再变成锐角.
探索新知
在这个过程中:
(1)这个四边形总是平行四边形吗?
(2)当α =90°时,其余三个内角各是多少度的角?
(3)当α =90°时,两条对角线的长有什么关系?
探索新知
归 纳
矩形既是中心对称图形,也是轴对称图形.
探索新知
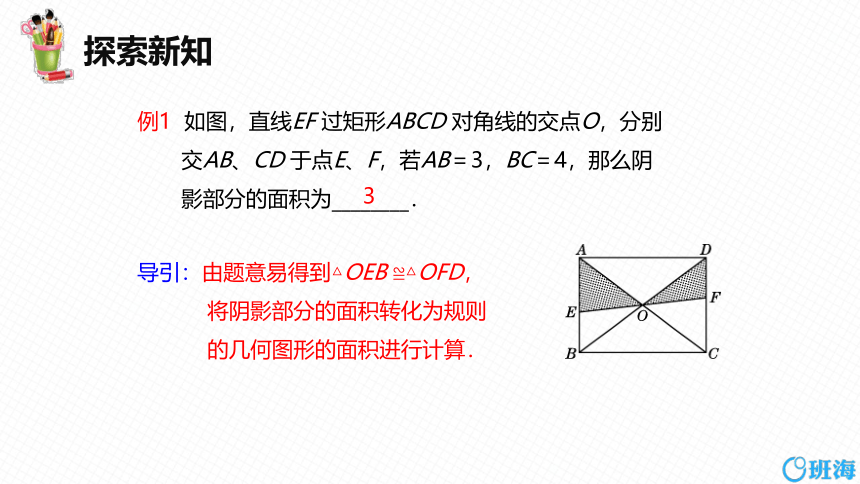
例1 如图,直线EF 过矩形ABCD 对角线的交点O,分别交AB、CD 于点E、F,若AB=3,BC=4,那么阴影部分的面积为________.
导引:由题意易得到△OEB ≌△OFD,
将阴影部分的面积转化为规则
的几何图形的面积进行计算.
3
探索新知
方法一:∵四边形ABCD 是矩形,
∴由矩形中心对称的性质知S△EBO=S△FDO,
∴阴影部分的面积为矩形面积的 .
∴S阴影部分=S△ABO= ×3×4=3.
方法二:在矩形ABCD 中,OB=OD,∠EBO=∠FDO.
在△OEB 与△OFD 中,
∴△OEB ≌△OFD.
∴S阴影部分=S△ABO= S矩形ABCD= ×3×4=3.
探索新知
总 结
矩形既是轴对称图形又是中心对称图形,根据对
称性将阴影部分的面积转化为规则的几何图形的面积
求解.体现了转化思想.
典题精讲
下列说法不正确的是( )
A.矩形是平行四边形
B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形
D.矩形既是轴对称图形又是中心对称图形
1
B
典题精讲
在 ABCD 中,AB=3,BC=4,连接AC,BD,当 ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠BAD+∠BCD=180°;
③AC⊥BD;④AC=BD.
A.①②③ B.①②④
C.②③④ D.①③④
2
B
探索新知
2
知识点
矩形的边角性质
因为矩形是平行四边形,所以它具有平行四边形
的所有性质.由于它有一个角为直角,它是否具有一般
平行四边形不具有的一些特殊性质呢?
思考
探索新知
(1)取一张矩形的纸片,分别沿它的两组对边的中点所在
的直线折叠,你发现矩形是轴对称图形吗?如果是,它
有几条对称轴?
(2)利用矩形的轴对称性质,由矩形的一个角是直角,你
发现矩形的另外三个角有什么性质?证明你的结论.
探索新知
归 纳
矩形的四个角都是直角.
探索新知
例2 如图所示,在矩形ABCD 中,AE⊥BD 于点E, ∠DAE∶∠BAE=3∶1,求∠BAO 和∠EAO 的度数.
由∠DAE 与∠BAE 之和为矩形
的一个内角及两角之比即可求
出∠DAE 和∠BAE 的度数,从
而得出∠ABE 的度数,由矩形的性质易得∠BAO=
∠ABE,即可求出∠BAO 的度数,再由∠EAO=
∠BAO-∠BAE 可得∠EAO 的度数.
导引:
探索新知
∵四边形ABCD 是矩形,
∴∠DAB=90°,AO= AC,BO= BD,AC=BD.
∴∠BAE+∠DAE=90°,AO=BO.
又∵∠DAE∶∠BAE=3∶1,
∴∠BAE=22.5°,∠DAE=67.5°.
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°.
∵AO=BO,∴∠BAO=∠ABE=67.5°.
∴∠EAO=∠BAO-∠BAE=67.5°-22.5°=45°.
解:
探索新知
总 结
矩形的每条对角线把矩形分成两个直角三角形,
矩形的两条对角线将矩形分成四个等腰三角形,因此
有关矩形的计算问题经常通过转化到直角三角形和等
腰三角形中来解决.
典题精讲
1 已知:如图,E 为矩形ABCD 的边AD 的中点,连接BE,CE. 求证:△EBC 是等腰三角形.
在矩形ABCD 中,AB=CD,
∠A=∠D=90°,
∵E 为AD 的中点,∴AE=DE,
在△ABE 和△DCE 中,
∴△ABE ≌△DCE.
∴EB=EC,∴△EBC 是等腰三角形.
解:
典题精讲
如图,在矩形ABCD 中,AB=3,AD=4,对角线AC 与BD 相交于点O,EF 经过点O 且分别与AB,CD 相交于点E,F,则图中阴影部分的面积为________.
2
3
典题精讲
如图,点E 是矩形ABCD 的边AD 延长线上的一点,且AD=DE,连接BE 交CD 于点O,连接AO,下列结论中不正确的是( )
A.△AOB ≌△BOC
B.△BOC ≌△EOD
C.△AOD ≌△EOD
D.△AOD ≌△BOC
3
A
典题精讲
如图,点O 是矩形ABCD 的对角线AC 的中点,OM∥AB交AD 于点M,若OM=3,BC=10,则OB 的长为( )
A.5 B.4
C. D.
4
D
典题精讲
如图,在矩形纸片ABCD 中,AD=4 cm,把纸片沿直线AC 折叠,点B 落在E 处,AE 交DC 于点O. 若AO=5 cm,则AB 的长为( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
5
C
探索新知
3
知识点
矩形的对角线性质
任意画一个矩形,作出它的两条对角线,并比较它们
的长.你有什么发现
已知:如图所示,四边形ABCD 是矩形.
求证:AC=DB.
A
B
C
D
O
探索新知
证明:∵四边形ABCD 是矩形,
∴∠ABC=∠DCB=90°(矩形的性质定理1).
∵AB=CD (平行四边形的对边相等),BC=CB.
∴△ABC ≌△DCB (SAS).
∴AC=DB.
于是,就得到矩形的性质:矩形的对角线相等.
探索新知
归 纳
矩形的对角线相等.
∵四边形ABCD 是矩形,
∴AC=BD,AO=OC=BO=OD.
∵∠AOD=120°,∴∠AOB=60°.
∴∠AOB 是等边三角形.
∴AO=BO=AB=4 cm,AC=AO+OC=AO+OB=8(cm),
即矩形ABCD 对角线的长为8 cm.
探索新知
例4 如图,矩形ABCD 两条对角线相交于点O, ∠AOD=120°,AB=4 cm.求矩形对角线的长.
解:
A
B
C
D
O
探索新知
总 结
因为矩形的对角线相等且互相平分,所以矩形的
对角线将矩形分成了四个等腰三角形,再由特殊角可
得到特殊的三角形——等边三角形,利用等边三角形
的性质即可求解.
典题精讲
矩形具有而一般平行四边形不一定具有的性质是__________________________________________________________________________.
1
①矩形的四个内角都是直角;
②矩形的两条对角线相等
典题精讲
如图,四边形ABCD 为矩形,指
出图中相等的线段和角.
2
相等的线段:AB=CD,AD=BC,
AC=BD,OA=OC=OB=OD.
相等的角:∠BAD=∠ADC=∠BCD=∠ABC,∠AOB=∠DOC,∠AOD=∠BOC,
∠OAB=∠ABO=∠ODC=∠OCD,
∠OAD=∠ODA=∠OBC=∠OCB.
解:
A
B
C
D
O
典题精讲
已知矩形ABCD 的边AB=4,BC=5.求对角线AC 的长.
3
如图,在矩形ABCD 中,
AB=4,BC=5,∠ABC=90°.
∴AC=
解:
A
B
C
D
典题精讲
如图,在矩形ABCD 中,E 为AD上一点,EF丄CE,交AB于点F,DE=2. 矩影的周长为16,且CE=EF. 求AE 的长.
4
典题精讲
在矩形ABCD 中,∠A=∠D=90°,AD=BC,AB=CD,∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,∵∠DEC+∠DCE=90°,∴∠AEF=∠DCE.
在△AEF 和△DCE 中,
∴△AEF ≌△DCE,
∴AE=CD,设AE=x,则CD=x,AD=x+2.
∵矩形的周长为16,∴2(x+x+2)=16.解得x=3.
即AE=3.
解:
在矩形ABCD 中,
AB∥CD,AC=BD,
因为AB∥CE,BE∥AC,
所以四边形ABEC 是平行四边形.
所以AC=BE,又因为AC=BD,所以BD=BE.
典题精讲
已知:如图,在矩形ABCD 中,对角线AC,BD 相交于点O,过点B 作BE∥AC,交DC 的延长线于点E.求证:BD=BE.
5
证明:
连接PO,在矩形ABCD 中,
AC=BD=
=5.OA=OD= AC= BD= .
S△AOD=S△AOP+S△DOP= OA ·PE+ OD ·PF=
OA· (PE+PF )= S△ADC= × AD ·DC=3.
故PE+PF= .
典题精讲
已知:如图,在矩形ABCD 中, AB=3,AD=4,P 为AD上一点,过点P 作PE⊥AC,PF⊥BD,垂足分别为E,F.求PE+PF 的值.
6
解:
典题精讲
如图,在矩形ABCD 中,AB=3,AD=4,E 为CD 的中点,连接AE 并延长,交BC 的延长线于点F,连接DF.求DF 的长.
7
典题精讲
连接AC,在矩形ABCD 中,AD∥BC,AD=BC,∠ADC=∠DCF=90°,因为E 为CD 的中点,所以DE=CE.因为AD∥CF,所以∠DAE=∠CFE.
在△ADE 和△FCE 中,
所以△ADE ≌△FCE,
所以CF=AD,又因为AD=BC,所以BC=CF,
又因为DC⊥BF,
所以DF=BD= =5.
解:
典题精讲
如图,在矩形ABCD 中,对角线AC,BD 相交于点O,∠AOB=60°,AC=6 cm,则AB 的长是( )
A.3 cm
B.6 cm
C.10 cm
D.12 cm
8
A
典题精讲
9
如图,矩形ABCD 的对角线AC 与BD 相交于点O,CE∥BD,DE∥AC,AD= DE=2,则四边形OCED 的面积为( )
A.2
B.4
C.4
D.8
A
易错提醒
矩形一个角的平分线分矩形一边为1 cm和3 cm两部分,则这个矩形的面积为 .
4 cm2或12 cm2
易错点:对题意理解不透彻导致漏解.
学以致用
小试牛刀
在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图所示的图形.该图中,四边形ABCD 是矩形,E 是BA 延长线上一点,F 是CE 上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD 的度数是( )
A.7°
B.21°
C.23°
D.24°
1
C
小试牛刀
如图,点P 是矩形ABCD 的边AD上的一动点,矩形的两条边AB,BC 的长分别是6和8,则点P 到矩形的两条对角线AC 和BD 的距离之和是( )
A.4.8
B.5
C.6
D.7.2
A
2
小试牛刀
3
在矩形ABCD 中,E、F 分别是AD、BC 的中点,CE、AF 分别交BD 于G、H 两点.
求证:(1)四边形AFCE 是平行四边形;
(2)EG=FH.
小试牛刀
(1)∵四边形ABCD 是矩形,
∴AD∥BC,AD=BC.
∵E、F 分别是AD、BC 的中点,
∴AE= AD,CF= BC.
∴AE=CF.
∴四边形AFCE 是平行四边形.
证明:
小试牛刀
(2)∵四边形AFCE 是平行四边形,
∴CE∥AF.
∴∠DGE=∠AHD=∠BHF.
∵AD∥BC,∴∠EDG=∠FBH.
∵DE= AD,BF= BC,AD=BC,
∴DE=BF.
在△DEG 和△BFH 中,
∴△DEG ≌△BFH (AAS).
∴EG=FH.
小试牛刀
4
如图,矩形ABCD 的对角线AC,BD 相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD 的面积.
小试牛刀
(1)∵四边形ABCD 是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,∴OE=OF.
在△AOE 和△COF 中,
∴△AOE ≌△COF (SAS).
∴AE=CF.
证明:
小试牛刀
(2)∵OA=OC,OB=OD,AC=BD,∴OA=OB.
∵∠AOB=∠COD=60°.
∴△AOB 是等边三角形.
∴OA=AB=6.∴AC=2OA=12.
在Rt△ABC 中,BC= =6 ,
∴矩形ABCD 的面积为AB ·BC=6×6 =36 .
解:
小试牛刀
5
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徵》)
小试牛刀
请根据该图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC ),S矩形EBMF=S△ABC-(________+________).
易知,S△ADC=S△ABC,________=________,________=________.
可得S矩形NFGD=S矩形EBMF
S△AEF
S△FMC
S△ANF
S△AEF
S△FGC
S△FMC
小试牛刀
6
如图,以△ABC 的三边为边在BC 的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF,连接DE,EF.请回答下列问题:
(1)四边形ADEF 是什么四边形?并说明理由.
(2)当△ABC 满足什么条件时,四边形ADEF 是矩形?
小试牛刀
(1)四边形ADEF 是平行四边形.
理由:∵△ABD,△BEC 都是等边三角形,
∴BD=AB=AD,BE=BC,
∠DBA=∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC.
∴△DBE ≌△ABC.∴DE=AC.
又∵△ACF 是等边三角形,∴AC=AF.∴DE=AF.
同理可得△ABC ≌△FEC,∴EF=BA=DA.
∵DE=AF,DA=EF,
∴四边形ADEF 为平行四边形.
解:
小试牛刀
(2)若四边形ADEF 为矩形,则∠DAF=90°.
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=360°
-60°-60°-90°=150°.
∴当△ABC 满足∠BAC=150°时,四边形ADEF 是矩形.
课堂小结
课堂小结
1. 矩形是特殊的平行四边形,具有平行四边形的所有性质,它的特殊性就是四个角都是直角和对角线相等.
2. 矩形的两条对角线将矩形分为两对全等的等腰三角形.在解题的时候常用到等腰三角形的性质.
3. 矩形既是中心对称图形又是轴对称图形,有两条对称轴.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.4 矩 形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
两组对边分别平行的四边形是平行四边形.
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
情景导入
我们已经知道平行四边形是特殊的四边形,因此
平行四边形除具有四边形的性质外,还有它的特殊性
质,同样对于平行四边形来说有特殊情况即特殊的平
行四边形,也,这堂课我们就来研究一种恃殊的平行
四边形——矩形.
一个角是
直角
两组对边
分别平行
平行
四边形
矩形
新课精讲
探索新知
知识点
矩形及其对称性
1. 如图,剪出一个矩形纸片ABCD ,点O 是这个矩形
的中心.请你用折叠的方法,验证它是轴对称图形.
矩形有几条对称轴.它们都经过矩形的中心吗?
1
探索新知
2. 四边形具有不稳定性,即当一个四边形的四条边长
保持不变时,它的形状却是可以改变的.如图,使
一个平行四边形保持四条边长不变,而将一个内角
α由钝角先变成直角,再变成锐角.
探索新知
在这个过程中:
(1)这个四边形总是平行四边形吗?
(2)当α =90°时,其余三个内角各是多少度的角?
(3)当α =90°时,两条对角线的长有什么关系?
探索新知
归 纳
矩形既是中心对称图形,也是轴对称图形.
探索新知
例1 如图,直线EF 过矩形ABCD 对角线的交点O,分别交AB、CD 于点E、F,若AB=3,BC=4,那么阴影部分的面积为________.
导引:由题意易得到△OEB ≌△OFD,
将阴影部分的面积转化为规则
的几何图形的面积进行计算.
3
探索新知
方法一:∵四边形ABCD 是矩形,
∴由矩形中心对称的性质知S△EBO=S△FDO,
∴阴影部分的面积为矩形面积的 .
∴S阴影部分=S△ABO= ×3×4=3.
方法二:在矩形ABCD 中,OB=OD,∠EBO=∠FDO.
在△OEB 与△OFD 中,
∴△OEB ≌△OFD.
∴S阴影部分=S△ABO= S矩形ABCD= ×3×4=3.
探索新知
总 结
矩形既是轴对称图形又是中心对称图形,根据对
称性将阴影部分的面积转化为规则的几何图形的面积
求解.体现了转化思想.
典题精讲
下列说法不正确的是( )
A.矩形是平行四边形
B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形
D.矩形既是轴对称图形又是中心对称图形
1
B
典题精讲
在 ABCD 中,AB=3,BC=4,连接AC,BD,当 ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠BAD+∠BCD=180°;
③AC⊥BD;④AC=BD.
A.①②③ B.①②④
C.②③④ D.①③④
2
B
探索新知
2
知识点
矩形的边角性质
因为矩形是平行四边形,所以它具有平行四边形
的所有性质.由于它有一个角为直角,它是否具有一般
平行四边形不具有的一些特殊性质呢?
思考
探索新知
(1)取一张矩形的纸片,分别沿它的两组对边的中点所在
的直线折叠,你发现矩形是轴对称图形吗?如果是,它
有几条对称轴?
(2)利用矩形的轴对称性质,由矩形的一个角是直角,你
发现矩形的另外三个角有什么性质?证明你的结论.
探索新知
归 纳
矩形的四个角都是直角.
探索新知
例2 如图所示,在矩形ABCD 中,AE⊥BD 于点E, ∠DAE∶∠BAE=3∶1,求∠BAO 和∠EAO 的度数.
由∠DAE 与∠BAE 之和为矩形
的一个内角及两角之比即可求
出∠DAE 和∠BAE 的度数,从
而得出∠ABE 的度数,由矩形的性质易得∠BAO=
∠ABE,即可求出∠BAO 的度数,再由∠EAO=
∠BAO-∠BAE 可得∠EAO 的度数.
导引:
探索新知
∵四边形ABCD 是矩形,
∴∠DAB=90°,AO= AC,BO= BD,AC=BD.
∴∠BAE+∠DAE=90°,AO=BO.
又∵∠DAE∶∠BAE=3∶1,
∴∠BAE=22.5°,∠DAE=67.5°.
∵AE⊥BD,
∴∠ABE=90°-∠BAE=90°-22.5°=67.5°.
∵AO=BO,∴∠BAO=∠ABE=67.5°.
∴∠EAO=∠BAO-∠BAE=67.5°-22.5°=45°.
解:
探索新知
总 结
矩形的每条对角线把矩形分成两个直角三角形,
矩形的两条对角线将矩形分成四个等腰三角形,因此
有关矩形的计算问题经常通过转化到直角三角形和等
腰三角形中来解决.
典题精讲
1 已知:如图,E 为矩形ABCD 的边AD 的中点,连接BE,CE. 求证:△EBC 是等腰三角形.
在矩形ABCD 中,AB=CD,
∠A=∠D=90°,
∵E 为AD 的中点,∴AE=DE,
在△ABE 和△DCE 中,
∴△ABE ≌△DCE.
∴EB=EC,∴△EBC 是等腰三角形.
解:
典题精讲
如图,在矩形ABCD 中,AB=3,AD=4,对角线AC 与BD 相交于点O,EF 经过点O 且分别与AB,CD 相交于点E,F,则图中阴影部分的面积为________.
2
3
典题精讲
如图,点E 是矩形ABCD 的边AD 延长线上的一点,且AD=DE,连接BE 交CD 于点O,连接AO,下列结论中不正确的是( )
A.△AOB ≌△BOC
B.△BOC ≌△EOD
C.△AOD ≌△EOD
D.△AOD ≌△BOC
3
A
典题精讲
如图,点O 是矩形ABCD 的对角线AC 的中点,OM∥AB交AD 于点M,若OM=3,BC=10,则OB 的长为( )
A.5 B.4
C. D.
4
D
典题精讲
如图,在矩形纸片ABCD 中,AD=4 cm,把纸片沿直线AC 折叠,点B 落在E 处,AE 交DC 于点O. 若AO=5 cm,则AB 的长为( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
5
C
探索新知
3
知识点
矩形的对角线性质
任意画一个矩形,作出它的两条对角线,并比较它们
的长.你有什么发现
已知:如图所示,四边形ABCD 是矩形.
求证:AC=DB.
A
B
C
D
O
探索新知
证明:∵四边形ABCD 是矩形,
∴∠ABC=∠DCB=90°(矩形的性质定理1).
∵AB=CD (平行四边形的对边相等),BC=CB.
∴△ABC ≌△DCB (SAS).
∴AC=DB.
于是,就得到矩形的性质:矩形的对角线相等.
探索新知
归 纳
矩形的对角线相等.
∵四边形ABCD 是矩形,
∴AC=BD,AO=OC=BO=OD.
∵∠AOD=120°,∴∠AOB=60°.
∴∠AOB 是等边三角形.
∴AO=BO=AB=4 cm,AC=AO+OC=AO+OB=8(cm),
即矩形ABCD 对角线的长为8 cm.
探索新知
例4 如图,矩形ABCD 两条对角线相交于点O, ∠AOD=120°,AB=4 cm.求矩形对角线的长.
解:
A
B
C
D
O
探索新知
总 结
因为矩形的对角线相等且互相平分,所以矩形的
对角线将矩形分成了四个等腰三角形,再由特殊角可
得到特殊的三角形——等边三角形,利用等边三角形
的性质即可求解.
典题精讲
矩形具有而一般平行四边形不一定具有的性质是__________________________________________________________________________.
1
①矩形的四个内角都是直角;
②矩形的两条对角线相等
典题精讲
如图,四边形ABCD 为矩形,指
出图中相等的线段和角.
2
相等的线段:AB=CD,AD=BC,
AC=BD,OA=OC=OB=OD.
相等的角:∠BAD=∠ADC=∠BCD=∠ABC,∠AOB=∠DOC,∠AOD=∠BOC,
∠OAB=∠ABO=∠ODC=∠OCD,
∠OAD=∠ODA=∠OBC=∠OCB.
解:
A
B
C
D
O
典题精讲
已知矩形ABCD 的边AB=4,BC=5.求对角线AC 的长.
3
如图,在矩形ABCD 中,
AB=4,BC=5,∠ABC=90°.
∴AC=
解:
A
B
C
D
典题精讲
如图,在矩形ABCD 中,E 为AD上一点,EF丄CE,交AB于点F,DE=2. 矩影的周长为16,且CE=EF. 求AE 的长.
4
典题精讲
在矩形ABCD 中,∠A=∠D=90°,AD=BC,AB=CD,∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,∵∠DEC+∠DCE=90°,∴∠AEF=∠DCE.
在△AEF 和△DCE 中,
∴△AEF ≌△DCE,
∴AE=CD,设AE=x,则CD=x,AD=x+2.
∵矩形的周长为16,∴2(x+x+2)=16.解得x=3.
即AE=3.
解:
在矩形ABCD 中,
AB∥CD,AC=BD,
因为AB∥CE,BE∥AC,
所以四边形ABEC 是平行四边形.
所以AC=BE,又因为AC=BD,所以BD=BE.
典题精讲
已知:如图,在矩形ABCD 中,对角线AC,BD 相交于点O,过点B 作BE∥AC,交DC 的延长线于点E.求证:BD=BE.
5
证明:
连接PO,在矩形ABCD 中,
AC=BD=
=5.OA=OD= AC= BD= .
S△AOD=S△AOP+S△DOP= OA ·PE+ OD ·PF=
OA· (PE+PF )= S△ADC= × AD ·DC=3.
故PE+PF= .
典题精讲
已知:如图,在矩形ABCD 中, AB=3,AD=4,P 为AD上一点,过点P 作PE⊥AC,PF⊥BD,垂足分别为E,F.求PE+PF 的值.
6
解:
典题精讲
如图,在矩形ABCD 中,AB=3,AD=4,E 为CD 的中点,连接AE 并延长,交BC 的延长线于点F,连接DF.求DF 的长.
7
典题精讲
连接AC,在矩形ABCD 中,AD∥BC,AD=BC,∠ADC=∠DCF=90°,因为E 为CD 的中点,所以DE=CE.因为AD∥CF,所以∠DAE=∠CFE.
在△ADE 和△FCE 中,
所以△ADE ≌△FCE,
所以CF=AD,又因为AD=BC,所以BC=CF,
又因为DC⊥BF,
所以DF=BD= =5.
解:
典题精讲
如图,在矩形ABCD 中,对角线AC,BD 相交于点O,∠AOB=60°,AC=6 cm,则AB 的长是( )
A.3 cm
B.6 cm
C.10 cm
D.12 cm
8
A
典题精讲
9
如图,矩形ABCD 的对角线AC 与BD 相交于点O,CE∥BD,DE∥AC,AD= DE=2,则四边形OCED 的面积为( )
A.2
B.4
C.4
D.8
A
易错提醒
矩形一个角的平分线分矩形一边为1 cm和3 cm两部分,则这个矩形的面积为 .
4 cm2或12 cm2
易错点:对题意理解不透彻导致漏解.
学以致用
小试牛刀
在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图所示的图形.该图中,四边形ABCD 是矩形,E 是BA 延长线上一点,F 是CE 上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD 的度数是( )
A.7°
B.21°
C.23°
D.24°
1
C
小试牛刀
如图,点P 是矩形ABCD 的边AD上的一动点,矩形的两条边AB,BC 的长分别是6和8,则点P 到矩形的两条对角线AC 和BD 的距离之和是( )
A.4.8
B.5
C.6
D.7.2
A
2
小试牛刀
3
在矩形ABCD 中,E、F 分别是AD、BC 的中点,CE、AF 分别交BD 于G、H 两点.
求证:(1)四边形AFCE 是平行四边形;
(2)EG=FH.
小试牛刀
(1)∵四边形ABCD 是矩形,
∴AD∥BC,AD=BC.
∵E、F 分别是AD、BC 的中点,
∴AE= AD,CF= BC.
∴AE=CF.
∴四边形AFCE 是平行四边形.
证明:
小试牛刀
(2)∵四边形AFCE 是平行四边形,
∴CE∥AF.
∴∠DGE=∠AHD=∠BHF.
∵AD∥BC,∴∠EDG=∠FBH.
∵DE= AD,BF= BC,AD=BC,
∴DE=BF.
在△DEG 和△BFH 中,
∴△DEG ≌△BFH (AAS).
∴EG=FH.
小试牛刀
4
如图,矩形ABCD 的对角线AC,BD 相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD 的面积.
小试牛刀
(1)∵四边形ABCD 是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,∴OE=OF.
在△AOE 和△COF 中,
∴△AOE ≌△COF (SAS).
∴AE=CF.
证明:
小试牛刀
(2)∵OA=OC,OB=OD,AC=BD,∴OA=OB.
∵∠AOB=∠COD=60°.
∴△AOB 是等边三角形.
∴OA=AB=6.∴AC=2OA=12.
在Rt△ABC 中,BC= =6 ,
∴矩形ABCD 的面积为AB ·BC=6×6 =36 .
解:
小试牛刀
5
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徵》)
小试牛刀
请根据该图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC ),S矩形EBMF=S△ABC-(________+________).
易知,S△ADC=S△ABC,________=________,________=________.
可得S矩形NFGD=S矩形EBMF
S△AEF
S△FMC
S△ANF
S△AEF
S△FGC
S△FMC
小试牛刀
6
如图,以△ABC 的三边为边在BC 的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF,连接DE,EF.请回答下列问题:
(1)四边形ADEF 是什么四边形?并说明理由.
(2)当△ABC 满足什么条件时,四边形ADEF 是矩形?
小试牛刀
(1)四边形ADEF 是平行四边形.
理由:∵△ABD,△BEC 都是等边三角形,
∴BD=AB=AD,BE=BC,
∠DBA=∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA.
∴∠DBE=∠ABC.
∴△DBE ≌△ABC.∴DE=AC.
又∵△ACF 是等边三角形,∴AC=AF.∴DE=AF.
同理可得△ABC ≌△FEC,∴EF=BA=DA.
∵DE=AF,DA=EF,
∴四边形ADEF 为平行四边形.
解:
小试牛刀
(2)若四边形ADEF 为矩形,则∠DAF=90°.
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=360°
-60°-60°-90°=150°.
∴当△ABC 满足∠BAC=150°时,四边形ADEF 是矩形.
课堂小结
课堂小结
1. 矩形是特殊的平行四边形,具有平行四边形的所有性质,它的特殊性就是四个角都是直角和对角线相等.
2. 矩形的两条对角线将矩形分为两对全等的等腰三角形.在解题的时候常用到等腰三角形的性质.
3. 矩形既是中心对称图形又是轴对称图形,有两条对称轴.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
