【班海精品】冀教版(新)八下-22.5 菱形 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-22.5 菱形 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览








文档简介
(共61张PPT)
22.5 菱 形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,我们已经研究了一种特殊的平行四边形——矩形 ;这堂课还要研究另一种特殊的平行四边形——菱形.
情景导入
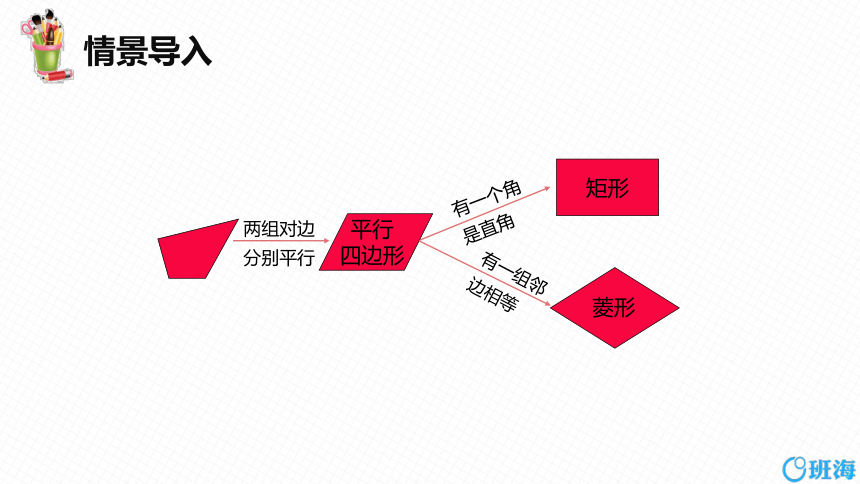
两组对边
分别平行
平行
四边形
矩形
菱形
有一个角
是直角
有一组邻
边相等
新课精讲
探索新知
1
知识点
菱形及其对称性
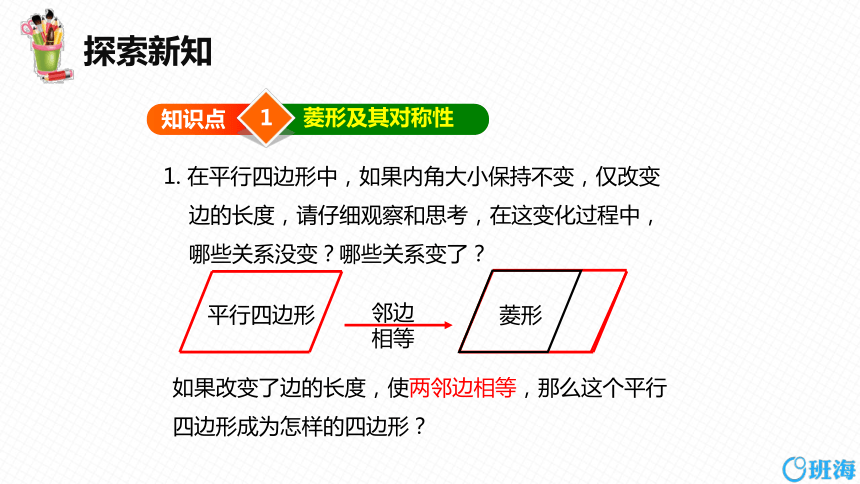
1. 在平行四边形中,如果内角大小保持不变,仅改变
边的长度,请仔细观察和思考,在这变化过程中,
哪些关系没变?哪些关系变了?
平行四边形
邻边相等
菱形
如果改变了边的长度,使两邻边相等,那么这个平行
四边形成为怎样的四边形?
探索新知
归 纳
定义:有一组邻边相等的平行四边形叫做菱形.
AB=BC
平行四边形ABCD
四边形ABCD是菱形
探索新知
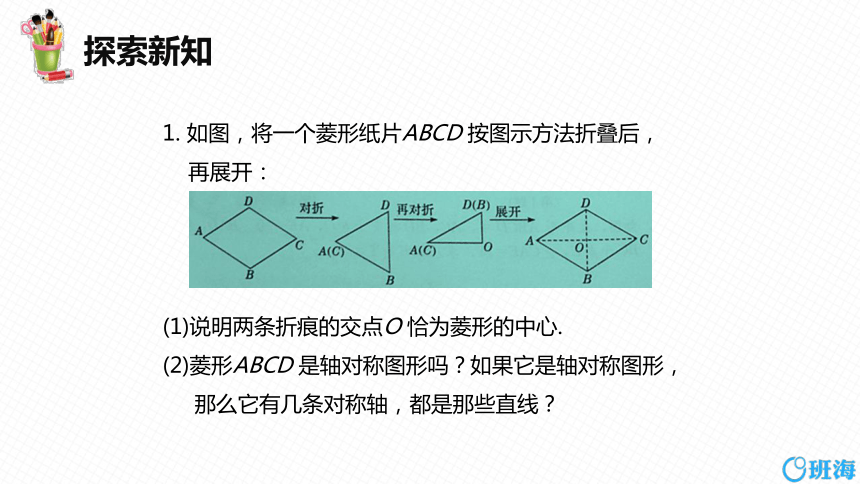
1. 如图,将一个菱形纸片ABCD 按图示方法折叠后,
再展开:
(1)说明两条折痕的交点O 恰为菱形的中心.
(2)菱形ABCD 是轴对称图形吗?如果它是轴对称图形,
那么它有几条对称轴,都是那些直线?
探索新知
归 纳
菱形既是中心对称图形,又是轴对称图形.
探索新知
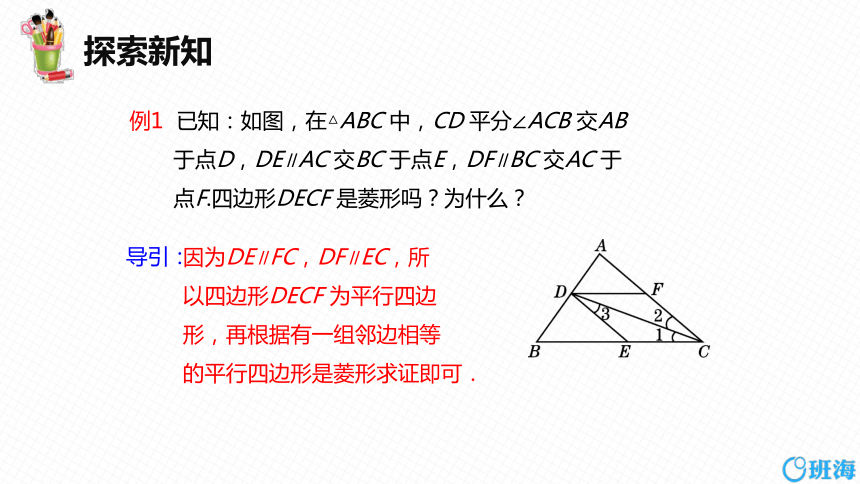
例1 已知:如图,在△ABC 中,CD 平分∠ACB 交AB于点D,DE∥AC 交BC 于点E,DF∥BC 交AC 于点F.四边形DECF 是菱形吗?为什么?
因为DE∥FC,DF∥EC,所
以四边形DECF 为平行四边
形,再根据有一组邻边相等
的平行四边形是菱形求证即可.
导引:
探索新知
四边形DECF 是菱形.理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF 为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD 平分∠ACB,
∴∠1=∠2,∴∠1=∠3,∴DE=EC,
∴平行四边形DECF 为菱形(有一组邻边相等的平
行四边形是菱形).
解:
探索新知
总 结
本题考查了菱形的定义,菱形的定义也可以作为菱形的判定方法.
典题精讲
如图,若要使 ABCD 成为菱形,则需要添加的条件是( )
A.AB=CD
B.AD=AC
C.AB=BC
D.AC=BD
1
C
典题精讲
2
如图,在△ABC 中,AB≠AC,D 是BC上一点,DE∥AC 交AB 于点E,DF∥AB 交AC 于点F,要使四边形AEDF 是菱形,只需添加的条件是( )
A.AD⊥BC
B.∠BAD=∠CAD
C.BD=DC
D.AD=BD
B
典题精讲
3
菱形是轴对称图形,其对称轴的条数为( )
A.2条 B.4条
C.6条 D.8条
A
探索新知
2
知识点
菱形边的性质
菱形具有平行四边形的所有性质.此外,菱形还
具有哪些特殊性质呢?观察图所示,根据菱形的轴对
称性,你发现菱形的四条边具有什么大小关系?
探索新知
归 纳
菱形的四条边都相等.
探索新知
例2 如图所示,菱形ABCD 中,∠B=60°,AB=2,E、F 分别是BC、CD 的中点,连接AE、EF、AF,则△AEF 的周长为( )
A. B. C. D.3
在菱形ABCD 中,因为∠B=60°,连接AC,则
△ABC 是等边三角形,又因为E 分别是BC 的中点,
所以AE 垂直于BC,因此AE= ,所以
△AEF 的周长为 ,故选B.
分析:
B
探索新知
总 结
在菱形中作辅助线经常连接对角线,构造三角形来做题,能够迎刃而解.
典题精讲
1 菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC= 45°,OC= 求点B 的坐标.
过点B 作BD⊥OA,垂足为D.
由题意可知∠BAD=∠AOC=45°,
AB=OA=OC= ,
所以AD=BD=1.
所以B 点的坐标为( +1,1).
解:
连接BD,
∵AB=2 cm,E 为AB 的中点,
∴AE= AB=1 cm.
在Rt△AED 中,
DE= (cm).
∴S菱形ABCD=2S△ABD=2× ×2× =2 (cm2).
典题精讲
如图,菱形ABCD 的边长为2 cm,E 为AB 的中点,且DE⊥AB. 求菱形ABCD 的面积.
2
解:
典题精讲
边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm
3
C
典题精讲
4
如图,在菱形ABCD 中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF 的面积是( )
A.4
B.3
C.2
D.
B
典题精讲
5
如图,在边长为6的菱形ABCD 中,∠DAB=60°,以点D 为圆心,菱形的高DF 为半径画弧,交AD 于点E,交CD 于点G,则图中阴影部分的面积是( )
A.18 -9π
B.18-3π
C.9 -
D.18 -3π
A
探索新知
3
知识点
菱形对角线的性质
因为菱形是平行四边形,所以它具有平行四边形的
所有性质.由于它的一组邻边相等,它是否具有一般平行
四边形不具有的一些特殊性质呢?
思考
菱形的两条对角线AC 与BD 之间具有什么位置关系
探索新知
归 纳
对于菱形,我们仍然从它的对角线等方面进行研究.可以发现并证明(请你自己完成证明),菱形还有以下性质:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
探索新知
问 题
菱形的面积如何计算呢?
菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积
时,要灵活运用使计算简单.
探索新知
例3 如图,菱形ABCD 的周长为16 cm,∠ABC= 120°.求对角线BD 和AC 的长.
∵AB+BC+CD+AD= 16 cm,
∴AB=BC=CD=AD= =4(cm).
∵BD 平分∠ABC,∠ABC= 120°,
∴∠ABD=60°.∴△ABD 是等边三角形.
∴BD=AB=4 cm.
在Rt△AOB 中,OB=2 cm,
解:
探索新知
总 结
菱形的对角线将菱形分成四个全等的直角三角形,我们通常将菱形问题中求相关线段的长转化为求直角三角形中相关线段的长,再利用勾股定理来计算.
典题精讲
如图,在菱形ABCD 中,AC,BD 为对角线,∠BAC=50°.求菱形ABCD 各内角的度数.
1
在菱形ABCD 中,
∵∠BAC=50°,
∴∠BAD=2∠BAC=100°.
∵AD∥BC,∴∠BAD+∠ABC=180°,
∴∠ABC=80°.∴∠ADC=80°,∠BCD=100°.
解:
A
B
C
D
典题精讲
在菱形ABCD 中,对角线AC=8,BD=6.
求菱形的周长.
2
解:由题意易知菱形的边长为 =5,
所以周长为4×5=20.
典题精讲
如图,菱形ABCD 的对角线AC,BD 相交于点O,且AC=6 cm,BD=8 cm,AE⊥BC,垂足为E.
求AE 的长.
3
典题精讲
在菱形ABCD 中,
∵AC=6 cm,BD=8 cm,
∴OA= AC=3 cm,OB= BD=4 cm.
∴在Rt△AOB 中,AB= =5 cm.
∴BC=5 cm.
∵S△ABC= AC ·OB= BC ·AE,
∴AE= (cm).
解:
典题精讲
如图,四边形ABCD 是菱形,A,B 两点的坐标分别为 (0,4),(-3,0).求点 D,C 的坐标.
4
∵A (0,4),B (-3,0),
∴OA=4,OB=3,
∴AB= =5.
∴AD=BC=AB=5.
∴D 点的坐标为(0,-1),
C 点的坐标为(-3,-5).
解:
探索新知
如图,菱形花坛ABCD 的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC 和BD. 求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
例4
探索新知
∵花坛ABCD 的形状是菱形,
∴AC⊥BD,∠ABO = ∠ABC = × 60°= 30°.
在Rt△OAB 中,AO = AB = ×20=10,
∴花坛的两条小路长AC = 2AO =20 (m),
BD = 2BO =20 ≈34. 64 (m).
花坛的面积S四边形ABCD=4×S△OAB= AC ·BD =200 ≈346. 4 (m2).
解:
探索新知
总 结
菱形的面积有三种计算方法:
(1)将其看成平行四边形,用底与高的积来求;
(2)对角线分得的四个全等直角三角形面积之和;
(3)两条对角线乘积的一半.
说明:读者可利用(1)(2)两种方法试一试;注意应
用(3)这种方法时不要忽视“一半”.
典题精讲
已知菱形的边长和一条对角线的长均为2 cm.
求这个菱形的面积.
1
解:由题意易知菱形的另一条对角线的长为 cm,所以该菱形的面积为 (cm2).
典题精讲
如图,菱形ABCD 的对角线相交于点O,延长AB至点E,使BE=BC,连接CE.
(1)求证:BD=EC.
(2)求证:S菱形ABCD=S△AEC
2
典题精讲
(1)在菱形ABCD 中,AB∥CD,
即BE∥CD,BC=CD,
∵BE=BC,∴BE=CD,
∴四边形BECD 为平行四边形.∴BD=EC.
(2)由题意易知S△ADC=S△ABC=S△BEC.
∵S菱形ABCD=S△ADC+S△ABC,
S△AEC=S△ABC+S△BEC,
∴S菱形ABCD=S△AEC.
解:
典题精讲
3
下列性质中菱形不一定具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.既是轴对称图形又是中心对称图形
C
典题精讲
4
已知菱形的周长为4 ,两条对角线的和为6,则菱形的面积为( )
A.2 B.
C.3 D.4
D
易错提醒
在菱形ABCD 中,∠A=30°.在同一平面内,以对角线BD 为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为______________.
45°或105°
易错点:考虑问题不全导致漏解.
学以致用
小试牛刀
如图,O 是菱形ABCD 的对角线AC,BD 的交点,E,F 分别是OA,OC 的中点,下列结论:
①S△ADE=S△EOD;②四边形BFDE 是轴对称图形;
③△DEF 是轴对称图形;④∠ADE=∠EDO.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
C
1
小试牛刀
如图,菱形ABCD 的边AB=8,∠B=60°,P 是AB上一点,BP=3,Q 是CD 边上一动点,将梯形APQD 沿直线PQ 折叠,A 的对应点为A′. 当CA′的长度最小时,CQ 的长为( )
A.5 B.7
C.8 D.
B
2
小试牛刀
如图,菱形ABCD 的对角线AC,BD 的长分别为6 cm,8 cm,则这个菱形的周长为( )
A.5 cm
B.10 cm
C.14 cm
D.20 cm
D
3
小试牛刀
4
如图,在 ABCD 中,BC=2AB=4,点E,F 分别是BC,AD 的中点.
(1)求证:△ABE ≌△CDF;
(2)当四边形AECF 为菱形时,求出该菱形的面积.
小试牛刀
(1)证明:∵四边形ABCD 为平行四边形,
∴AB=CD,∠B=∠D,BC=AD.
∵E,F 分别是BC,AD 的中点,
∴BE=DF,∴△ABE ≌△CDF.
(2)解:由题易知AB=BE=2.当四边形AECF 为菱形时,
AE=EC=BE=2.∴△ABE 为等边三角形.
如图,过点A 作AM⊥BE 于M,
则BM=1,
∴AM= .
∴菱形AECF 的面积为2× =2 .
小试牛刀
5
如图,在矩形ABCD 中,AB=6,BC=4,过对角线BD 中点O 的直线分别交AB,CD 边于点E,F.
(1)求证:四边形BEDF 是平行四边形;
(2)当四边形BEDF 是菱形时,求EF 的长.
小试牛刀
(1)∵四边形ABCD 是矩形,O 是BD 的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
在△BOE 和△DOF 中,
∴△BOE ≌△DOF (ASA).
∴EO=FO.
∴四边形BEDF 是平行四边形.
证明:
小试牛刀
(2)当四边形BEDF 是菱形时,BD⊥EF,BE=DE.
设BE=x,则DE=x,AE=6-x,
在Rt△ADE 中,DE 2=AD 2+AE 2,
∴x 2=42+(6-x )2,解得:x= ,
∵BD= ,
∴BO= BD= . ∵BD⊥EF,
∴EO= .
∴EF=2EO= .
解:
小试牛刀
6
如图,在菱形ABCD 中,对角线AC,BD 相交于点O,过点D 作对角线BD 的垂线交BA 的延长线于点E.
(1)求证:四边形ACDE 是平行四边形;
(2)若AC=8,BD=6,求△ADE 的周长.
小试牛刀
(1)证明:∵四边形ABCD 是菱形,
∴AB∥CD,AC⊥BD.
∵DE⊥BD,∴DE∥AC.
∴四边形ACDE 是平行四边形.
(2)解:∵四边形ABCD 是菱形,
AC=8,BD=6,
∴AO=4,DO=3.∴CD=AD=5.
∵四边形ACDE 是平行四边形,
∴AE=CD=5,DE=AC=8.
∴△ADE 的周长为AD+AE+DE=5+5+8=18.
小试牛刀
7
如图,四边形ABCD 是菱形,点E 为对角线AC上一点,
连接DE 并延长交AB 的延长线于点F.连接CF,BD,BE.
(1)求证:∠AFD=∠EBC;
(2)若E 为△BCD 的重心,求∠ACF 的度数.
小试牛刀
(1) ∵四边形ABCD 为菱形,
∴AB∥CD,DC=BC,∠DCE=∠BCE.
又∵CE=CE,
∴△DCE ≌△BCE (SAS).
∴∠EBC=∠EDC.
又∵AB∥CD,∴∠AFD=∠EDC.
∴∠AFD=∠EBC.
证明:
小试牛刀
(2)如图,设DF 交BC 于点P,AC 交BD 于点O,
∵E 为△BCD 的重心,
∴P 为BC 的中点.∴BP=CP.
又∵∠CDP=∠BFP,
∠CPD=∠BPF,
∴△CDP ≌△BFP (AAS).∴DP=FP.
∴四边形BFCD 是平行四边形.∴FC∥BD.
∵四边形ABCD 为菱形,
∴AC⊥BD.∴∠AOB=90°.
∴∠ACF=∠AOB=90°.
解:
课堂小结
课堂小结
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。
菱形的性质
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.5 菱 形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说有特殊情况即特殊的平行四边形,我们已经研究了一种特殊的平行四边形——矩形 ;这堂课还要研究另一种特殊的平行四边形——菱形.
情景导入
两组对边
分别平行
平行
四边形
矩形
菱形
有一个角
是直角
有一组邻
边相等
新课精讲
探索新知
1
知识点
菱形及其对称性
1. 在平行四边形中,如果内角大小保持不变,仅改变
边的长度,请仔细观察和思考,在这变化过程中,
哪些关系没变?哪些关系变了?
平行四边形
邻边相等
菱形
如果改变了边的长度,使两邻边相等,那么这个平行
四边形成为怎样的四边形?
探索新知
归 纳
定义:有一组邻边相等的平行四边形叫做菱形.
AB=BC
平行四边形ABCD
四边形ABCD是菱形
探索新知
1. 如图,将一个菱形纸片ABCD 按图示方法折叠后,
再展开:
(1)说明两条折痕的交点O 恰为菱形的中心.
(2)菱形ABCD 是轴对称图形吗?如果它是轴对称图形,
那么它有几条对称轴,都是那些直线?
探索新知
归 纳
菱形既是中心对称图形,又是轴对称图形.
探索新知
例1 已知:如图,在△ABC 中,CD 平分∠ACB 交AB于点D,DE∥AC 交BC 于点E,DF∥BC 交AC 于点F.四边形DECF 是菱形吗?为什么?
因为DE∥FC,DF∥EC,所
以四边形DECF 为平行四边
形,再根据有一组邻边相等
的平行四边形是菱形求证即可.
导引:
探索新知
四边形DECF 是菱形.理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF 为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD 平分∠ACB,
∴∠1=∠2,∴∠1=∠3,∴DE=EC,
∴平行四边形DECF 为菱形(有一组邻边相等的平
行四边形是菱形).
解:
探索新知
总 结
本题考查了菱形的定义,菱形的定义也可以作为菱形的判定方法.
典题精讲
如图,若要使 ABCD 成为菱形,则需要添加的条件是( )
A.AB=CD
B.AD=AC
C.AB=BC
D.AC=BD
1
C
典题精讲
2
如图,在△ABC 中,AB≠AC,D 是BC上一点,DE∥AC 交AB 于点E,DF∥AB 交AC 于点F,要使四边形AEDF 是菱形,只需添加的条件是( )
A.AD⊥BC
B.∠BAD=∠CAD
C.BD=DC
D.AD=BD
B
典题精讲
3
菱形是轴对称图形,其对称轴的条数为( )
A.2条 B.4条
C.6条 D.8条
A
探索新知
2
知识点
菱形边的性质
菱形具有平行四边形的所有性质.此外,菱形还
具有哪些特殊性质呢?观察图所示,根据菱形的轴对
称性,你发现菱形的四条边具有什么大小关系?
探索新知
归 纳
菱形的四条边都相等.
探索新知
例2 如图所示,菱形ABCD 中,∠B=60°,AB=2,E、F 分别是BC、CD 的中点,连接AE、EF、AF,则△AEF 的周长为( )
A. B. C. D.3
在菱形ABCD 中,因为∠B=60°,连接AC,则
△ABC 是等边三角形,又因为E 分别是BC 的中点,
所以AE 垂直于BC,因此AE= ,所以
△AEF 的周长为 ,故选B.
分析:
B
探索新知
总 结
在菱形中作辅助线经常连接对角线,构造三角形来做题,能够迎刃而解.
典题精讲
1 菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC= 45°,OC= 求点B 的坐标.
过点B 作BD⊥OA,垂足为D.
由题意可知∠BAD=∠AOC=45°,
AB=OA=OC= ,
所以AD=BD=1.
所以B 点的坐标为( +1,1).
解:
连接BD,
∵AB=2 cm,E 为AB 的中点,
∴AE= AB=1 cm.
在Rt△AED 中,
DE= (cm).
∴S菱形ABCD=2S△ABD=2× ×2× =2 (cm2).
典题精讲
如图,菱形ABCD 的边长为2 cm,E 为AB 的中点,且DE⊥AB. 求菱形ABCD 的面积.
2
解:
典题精讲
边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm
3
C
典题精讲
4
如图,在菱形ABCD 中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF 的面积是( )
A.4
B.3
C.2
D.
B
典题精讲
5
如图,在边长为6的菱形ABCD 中,∠DAB=60°,以点D 为圆心,菱形的高DF 为半径画弧,交AD 于点E,交CD 于点G,则图中阴影部分的面积是( )
A.18 -9π
B.18-3π
C.9 -
D.18 -3π
A
探索新知
3
知识点
菱形对角线的性质
因为菱形是平行四边形,所以它具有平行四边形的
所有性质.由于它的一组邻边相等,它是否具有一般平行
四边形不具有的一些特殊性质呢?
思考
菱形的两条对角线AC 与BD 之间具有什么位置关系
探索新知
归 纳
对于菱形,我们仍然从它的对角线等方面进行研究.可以发现并证明(请你自己完成证明),菱形还有以下性质:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
探索新知
问 题
菱形的面积如何计算呢?
菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积
时,要灵活运用使计算简单.
探索新知
例3 如图,菱形ABCD 的周长为16 cm,∠ABC= 120°.求对角线BD 和AC 的长.
∵AB+BC+CD+AD= 16 cm,
∴AB=BC=CD=AD= =4(cm).
∵BD 平分∠ABC,∠ABC= 120°,
∴∠ABD=60°.∴△ABD 是等边三角形.
∴BD=AB=4 cm.
在Rt△AOB 中,OB=2 cm,
解:
探索新知
总 结
菱形的对角线将菱形分成四个全等的直角三角形,我们通常将菱形问题中求相关线段的长转化为求直角三角形中相关线段的长,再利用勾股定理来计算.
典题精讲
如图,在菱形ABCD 中,AC,BD 为对角线,∠BAC=50°.求菱形ABCD 各内角的度数.
1
在菱形ABCD 中,
∵∠BAC=50°,
∴∠BAD=2∠BAC=100°.
∵AD∥BC,∴∠BAD+∠ABC=180°,
∴∠ABC=80°.∴∠ADC=80°,∠BCD=100°.
解:
A
B
C
D
典题精讲
在菱形ABCD 中,对角线AC=8,BD=6.
求菱形的周长.
2
解:由题意易知菱形的边长为 =5,
所以周长为4×5=20.
典题精讲
如图,菱形ABCD 的对角线AC,BD 相交于点O,且AC=6 cm,BD=8 cm,AE⊥BC,垂足为E.
求AE 的长.
3
典题精讲
在菱形ABCD 中,
∵AC=6 cm,BD=8 cm,
∴OA= AC=3 cm,OB= BD=4 cm.
∴在Rt△AOB 中,AB= =5 cm.
∴BC=5 cm.
∵S△ABC= AC ·OB= BC ·AE,
∴AE= (cm).
解:
典题精讲
如图,四边形ABCD 是菱形,A,B 两点的坐标分别为 (0,4),(-3,0).求点 D,C 的坐标.
4
∵A (0,4),B (-3,0),
∴OA=4,OB=3,
∴AB= =5.
∴AD=BC=AB=5.
∴D 点的坐标为(0,-1),
C 点的坐标为(-3,-5).
解:
探索新知
如图,菱形花坛ABCD 的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC 和BD. 求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
例4
探索新知
∵花坛ABCD 的形状是菱形,
∴AC⊥BD,∠ABO = ∠ABC = × 60°= 30°.
在Rt△OAB 中,AO = AB = ×20=10,
∴花坛的两条小路长AC = 2AO =20 (m),
BD = 2BO =20 ≈34. 64 (m).
花坛的面积S四边形ABCD=4×S△OAB= AC ·BD =200 ≈346. 4 (m2).
解:
探索新知
总 结
菱形的面积有三种计算方法:
(1)将其看成平行四边形,用底与高的积来求;
(2)对角线分得的四个全等直角三角形面积之和;
(3)两条对角线乘积的一半.
说明:读者可利用(1)(2)两种方法试一试;注意应
用(3)这种方法时不要忽视“一半”.
典题精讲
已知菱形的边长和一条对角线的长均为2 cm.
求这个菱形的面积.
1
解:由题意易知菱形的另一条对角线的长为 cm,所以该菱形的面积为 (cm2).
典题精讲
如图,菱形ABCD 的对角线相交于点O,延长AB至点E,使BE=BC,连接CE.
(1)求证:BD=EC.
(2)求证:S菱形ABCD=S△AEC
2
典题精讲
(1)在菱形ABCD 中,AB∥CD,
即BE∥CD,BC=CD,
∵BE=BC,∴BE=CD,
∴四边形BECD 为平行四边形.∴BD=EC.
(2)由题意易知S△ADC=S△ABC=S△BEC.
∵S菱形ABCD=S△ADC+S△ABC,
S△AEC=S△ABC+S△BEC,
∴S菱形ABCD=S△AEC.
解:
典题精讲
3
下列性质中菱形不一定具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.既是轴对称图形又是中心对称图形
C
典题精讲
4
已知菱形的周长为4 ,两条对角线的和为6,则菱形的面积为( )
A.2 B.
C.3 D.4
D
易错提醒
在菱形ABCD 中,∠A=30°.在同一平面内,以对角线BD 为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为______________.
45°或105°
易错点:考虑问题不全导致漏解.
学以致用
小试牛刀
如图,O 是菱形ABCD 的对角线AC,BD 的交点,E,F 分别是OA,OC 的中点,下列结论:
①S△ADE=S△EOD;②四边形BFDE 是轴对称图形;
③△DEF 是轴对称图形;④∠ADE=∠EDO.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
C
1
小试牛刀
如图,菱形ABCD 的边AB=8,∠B=60°,P 是AB上一点,BP=3,Q 是CD 边上一动点,将梯形APQD 沿直线PQ 折叠,A 的对应点为A′. 当CA′的长度最小时,CQ 的长为( )
A.5 B.7
C.8 D.
B
2
小试牛刀
如图,菱形ABCD 的对角线AC,BD 的长分别为6 cm,8 cm,则这个菱形的周长为( )
A.5 cm
B.10 cm
C.14 cm
D.20 cm
D
3
小试牛刀
4
如图,在 ABCD 中,BC=2AB=4,点E,F 分别是BC,AD 的中点.
(1)求证:△ABE ≌△CDF;
(2)当四边形AECF 为菱形时,求出该菱形的面积.
小试牛刀
(1)证明:∵四边形ABCD 为平行四边形,
∴AB=CD,∠B=∠D,BC=AD.
∵E,F 分别是BC,AD 的中点,
∴BE=DF,∴△ABE ≌△CDF.
(2)解:由题易知AB=BE=2.当四边形AECF 为菱形时,
AE=EC=BE=2.∴△ABE 为等边三角形.
如图,过点A 作AM⊥BE 于M,
则BM=1,
∴AM= .
∴菱形AECF 的面积为2× =2 .
小试牛刀
5
如图,在矩形ABCD 中,AB=6,BC=4,过对角线BD 中点O 的直线分别交AB,CD 边于点E,F.
(1)求证:四边形BEDF 是平行四边形;
(2)当四边形BEDF 是菱形时,求EF 的长.
小试牛刀
(1)∵四边形ABCD 是矩形,O 是BD 的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
在△BOE 和△DOF 中,
∴△BOE ≌△DOF (ASA).
∴EO=FO.
∴四边形BEDF 是平行四边形.
证明:
小试牛刀
(2)当四边形BEDF 是菱形时,BD⊥EF,BE=DE.
设BE=x,则DE=x,AE=6-x,
在Rt△ADE 中,DE 2=AD 2+AE 2,
∴x 2=42+(6-x )2,解得:x= ,
∵BD= ,
∴BO= BD= . ∵BD⊥EF,
∴EO= .
∴EF=2EO= .
解:
小试牛刀
6
如图,在菱形ABCD 中,对角线AC,BD 相交于点O,过点D 作对角线BD 的垂线交BA 的延长线于点E.
(1)求证:四边形ACDE 是平行四边形;
(2)若AC=8,BD=6,求△ADE 的周长.
小试牛刀
(1)证明:∵四边形ABCD 是菱形,
∴AB∥CD,AC⊥BD.
∵DE⊥BD,∴DE∥AC.
∴四边形ACDE 是平行四边形.
(2)解:∵四边形ABCD 是菱形,
AC=8,BD=6,
∴AO=4,DO=3.∴CD=AD=5.
∵四边形ACDE 是平行四边形,
∴AE=CD=5,DE=AC=8.
∴△ADE 的周长为AD+AE+DE=5+5+8=18.
小试牛刀
7
如图,四边形ABCD 是菱形,点E 为对角线AC上一点,
连接DE 并延长交AB 的延长线于点F.连接CF,BD,BE.
(1)求证:∠AFD=∠EBC;
(2)若E 为△BCD 的重心,求∠ACF 的度数.
小试牛刀
(1) ∵四边形ABCD 为菱形,
∴AB∥CD,DC=BC,∠DCE=∠BCE.
又∵CE=CE,
∴△DCE ≌△BCE (SAS).
∴∠EBC=∠EDC.
又∵AB∥CD,∴∠AFD=∠EDC.
∴∠AFD=∠EBC.
证明:
小试牛刀
(2)如图,设DF 交BC 于点P,AC 交BD 于点O,
∵E 为△BCD 的重心,
∴P 为BC 的中点.∴BP=CP.
又∵∠CDP=∠BFP,
∠CPD=∠BPF,
∴△CDP ≌△BFP (AAS).∴DP=FP.
∴四边形BFCD 是平行四边形.∴FC∥BD.
∵四边形ABCD 为菱形,
∴AC⊥BD.∴∠AOB=90°.
∴∠ACF=∠AOB=90°.
解:
课堂小结
课堂小结
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。
菱形的性质
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
