【班海精品】冀教版(新)八下-22.6 正方形 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-22.6 正方形 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览









文档简介
(共55张PPT)
22.6 正方形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
相传,上古神话人物伏羲在黄河边行走,得到龙马送来的“河图”(如下图所示),在洛水边又得到神龟送来的“洛书”.“河图”、“洛书”是几千年前的两幅图象,是正方形的图案,由点和线交织而成,充满了巧妙的数字关系,说明中华祖先很早对于几何和代数的研究. 充分显示了中华祖先的聪明才智.
新课精讲
探索新知
1
知识点
正方形的对称性
O
A
B
C
D
(A)
(B)
(C)
(D)
正方形的对称性:
正方形是中心对称图形,对称中心为点O;
又是轴对称图形,有四条对称轴.
探索新知
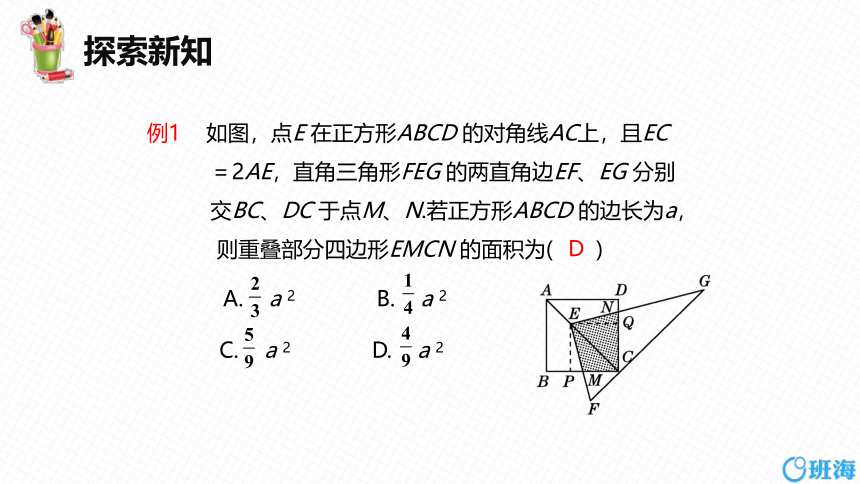
例1 如图,点E 在正方形ABCD 的对角线AC上,且EC
=2AE,直角三角形FEG 的两直角边EF、EG 分别
交BC、DC 于点M、N.若正方形ABCD 的边长为a,
则重叠部分四边形EMCN 的面积为( )
A. a 2 B. a 2
C. a 2 D. a 2
D
探索新知
作EP⊥BC 于点P,EQ⊥CD 于点Q,易得△EPM ≌△EQN,利用四边形EMCN 的面积等于正方形PCQE 的面积求解.
作EP⊥BC 于点P,EQ⊥CD 于点Q,
∵四边形ABCD 是正方形,∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG 是直角三角形,∴∠NEF=∠NEQ+∠MEQ=90°,∴∠PEM=∠NEQ,
∵CA 是∠BCD 的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE 是正方形,
导引:
探索新知
在△EPM 和△EQN 中,
∴△EPM ≌△EQN (ASA),∴S△EQN=S△EPM,
∴四边形EMCN 的面积等于正方形PCQE 的面积,
∵正方形ABCD 的边长为a,∴AC= a,
∵EC=2AE,∴EC= a,∴EP=PC= a,
∴正方形PCQE 的面积= a× a= a 2,
∴四边形EMCN 的面积= a 2.
探索新知
总 结
本例解法在于巧用割补法,将分散的图形拼合在
一起,将不规则的阴影面积集中到一个规则的图形中,
再利用正方形及三角形的性质求出,解答过程体现了
割补法及转化思想.
典题精讲
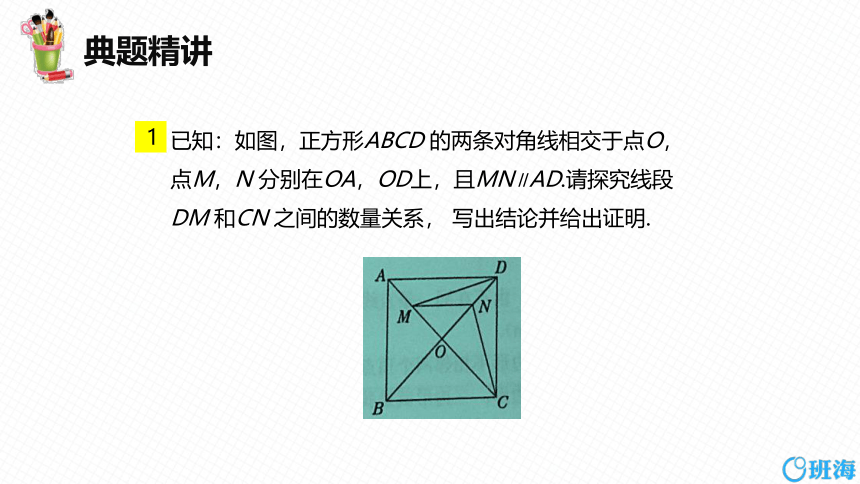
已知:如图,正方形ABCD 的两条对角线相交于点O,点M,N 分别在OA,OD上,且MN∥AD.请探究线段DM 和CN 之间的数量关系, 写出结论并给出证明.
1
典题精讲
DM=CN.
证明:∵四边形ABCD 是正方形,
∴OA=OD,AD=DC,∠DAM=∠CDN=45°.
又∵MN∥AD,
∴OM=ON.∴AM=DN.
∴△AMD ≌△DNC.
∴DM=CN.
解:
典题精讲
已知:如图,正方形ABCD 的两条对角线相交于点O,E 为OC上一点, AM⊥BE,垂足为M,AM 与DB 相交于点F. 求证:OE=OF.
2
典题精讲
在正方形ABCD 中,OA=OB,
∠BOC=∠AOF=90°.
∵在Rt△AME 中,∠EAM+∠AEM=90°,
在Rt△AOF 中,∠FAO+∠AFO=90°,
∴∠AEM=∠AFO.
∴△AOF ≌△BOE.
∴OE=OF.
证明:
典题精讲
3
如图,菱形ABCD 的面积为120 cm2,正方形AECF 的面积为50 cm2,则菱形的边长为________.
13cm
典题精讲
4
小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )
A.1次 B.2次
C.3次 D.4次
B
探索新知
2
知识点
正方形的判定
思考
正方形有哪些性质?如何判定一个四边形是正方形?
把它们写出来, 并和同学交流一下,然后证明其中的
一些结论.
探索新知
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
探索新知
归 纳
正方形的判定方法:要判定一个四边形是正方形,最
常用的方法就是先证明它是菱形(或矩形),再证明这
个菱形(或矩形)有一个角是直角(或有一组邻边相等),
其实质就是根据正方形的定义来判定,当然也可以先
证四边形是平行四边形,再证有一组邻边相等且有一
个角是直角,或证这个平行四边形的对角线相等并且
互相垂直.
探索新知
例2 如图,△ABC 中,AB=AC,AD 是△ABC 的角平分线,点O 为AB 的中点,连接DO 并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD 是矩形.
(2)当△ABC 满足什么条件时,矩形AEBD 是正方形?并说明理由.
探索新知
(1)利用平行四边形的判定方法首先得出四边形
AEBD 是平行四边形,进而由等腰三角形的
性质得出∠ADB=90°,即可证得结论;
(2)利用等腰直角三角形的性质得出AD=BD=
CD,进而利用正方形的判定方法即可判定
矩形AEBD 是正方形.
导引:
探索新知
(1)证明:∵点O 为AB 的中点,OE=OD,
∴四边形AEBD 是平行四边形.
∵AB=AC,AD 是△ABC 的角平分线,
∴AD⊥BC.∴∠ADB=90°.
∴平行四边形AEBD 是矩形.
(2)解:当∠BAC=90°时,矩形AEBD 是正方形.
理由:∵∠BAC=90°,AB=AC,AD 是△ABC
的角平分线,∴AD=BD=CD.
∵由(1)得四边形AEBD 是矩形,
∴矩形AEBD 是正方形.
探索新知
总 结
本题运用演绎推理解答,(1)中根据对角线互相平
分判定四边形AEBD是平行四边形,再由等腰三角形
三线合一的性质证直角,从而判定四边形AEBD是矩
形.(2)中添加条件后可证得矩形的一组邻边相等,即
可判定该矩形是正方形.
探索新知
例3 如图,已知在 ABCD 中,对角线AC,BD 交于点O,E
是BD 的延长线上的点,且EA=EC.
(1)求证:四边形ABCD 是菱形;
(2)若∠DAC=∠EAD+∠AED,
求证:四边形ABCD 是正方形.
要证 ABCD 是正方形,有三种途径可走:即在平行四
边形、菱形、矩形的基础上,找各需补充的对角线的
条件进行证明;若要证明 ABCD 是菱形,由于题中条
件与对角线相关,则需证AC⊥BD.
导引:
探索新知
(1)首先根据平行四边形的性质可得AO=CO,再由EA
=EC 可得△EAC 是等腰三角形,然后根据等腰三角
形三线合一的性质可得EO⊥AC,根据对角线互相
垂直的平行四边形是菱形可证出结论;
(2)首先根据角的关系得出AO=DO,进而得到AC=
BD,再根据对角线相等的菱形是正方形可得到结论.
探索新知
(1)∵四边形ABCD 是平行四边形,∴AO=CO,
∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD 是菱形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD 是菱形,
∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD 是正方形.
证明:
探索新知
总 结
证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
典题精讲
1 如图,把一张矩形纸片折叠,把重叠部分剪下来,展开后可以得到一个怎样的四边形?为什么?
正方形.因为有三个角是直角,
所以是矩形,由折叠可知一组邻边相等,所以是正方形.
解:
典题精讲
2
如图,在菱形ABCD 中,对角线AC,BD 相交于点O,不添加任何辅助线,请添加一个条件___________________________,使四边形ABCD是正方形.
∠BAD=90°(答案不唯一)
典题精讲
3
下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形
D
典题精讲
4
关于 ABCD 的叙述,正确的是( )
A.若AB⊥BC,则 ABCD 是菱形
B.若AC⊥BD,则 ABCD 是正方形
C.若AC=BD,则 ABCD 是矩形
D.若AB=AD,则 ABCD 是正方形
C
典题精讲
5
小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD 中选两个作为补充条件,使 ABCD 为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①②
B.②③
C.①③
D.②④
B
易错提醒
四边形ABCD 的对角线AC 和BD 相交于点O,假设有下列条件:①AB=AD; ②∠DAB=90°;
③AO=CO,BO=DO; ④四边形ABCD 为矩形;
⑤四边形ABCD 为菱形; ⑥四边形ABCD 为正方形.
则下列推理不成立的是( )
A.①④ ⑥ B.①③ ⑤
C.①② ⑥ D.②③ ④
易错点:将特殊四边形的判定相混淆导致出错
C
学以致用
小试牛刀
将五个边长都为2 cm的正方形按如图所示方式摆放,点A,B,C,D 分别是四个正方形的中心,则图中四块阴影部分面积的和为( )
A.2 cm2
B.4 cm2
C.6 cm2
D.8 cm2
B
1
小试牛刀
在△ABC 中,点D,E,F 分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,AD,则下列三种说法:
①如果EF=AD,那么四边形AEDF 是矩形;
②如果EF⊥AD,那么四边形AEDF 是菱形;
③如果AD⊥BC 且AB=AC,那么四边形AEDF 是正方形,其中正确的有( )
A.3个 B.2个
C.1个 D.0个
B
2
小试牛刀
3
已知:如图,在菱形ABCD 中,点E,O,F 分别为AB,AC,AD 的中点,连接CE,CF,OE,OF.
(1)求证:△BCE ≌△DCF.
(2)当AB 与BC 满足什么关系时,四边形AEOF 是正方形?请说明理由.
小试牛刀
(1)∵四边形ABCD 是菱形,
∴AB=BC=CD=DA,∠B=∠D.
∵点E,F 分别为AB,AD 的中点,
∴BE= AB,DF= AD.
∴BE=DF.
在△BCE 和△DCF 中,
∴△BCE ≌△DCF (SAS).
证明:
小试牛刀
(2)AB⊥BC,理由如下:
∵点E,O,F 分别为AB,AC,AD 的中点,
∴OE= BC= AD=AF.
同理可证:OF=AE= AB;
∴OE=OF=AF=AE.
∴四边形AEOF 是菱形.
∵AB⊥BC,又易知OE∥BC,∴AE⊥OE.
∴四边形AEOF 是正方形.
解:
小试牛刀
4
如图,已知在△ABC 中,AB=AC,D 为BC 边的中点,过点D 作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED ≌△CFD;
(2)若∠A=90°,求证:四边形DFAE 是正方形.
小试牛刀
(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D 是BC 的中点,∴BD=CD.
∴△BED ≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∵∠A=90°,∴四边形DFAE 为矩形.
∵△BED ≌△CFD,∴DE=DF.
∴四边形DFAE 是正方形.
证明:
小试牛刀
5
定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD 的长.
②若AC⊥BD,
求证:AD=CD.
小试牛刀
(1)①∵AB=CD=1,AB∥CD,
∴四边形ABCD 是平行四边形.
又∵AB=BC,
∴四边形ABCD 是菱形.
又∵∠ABC=90°,
∴四边形ABCD 是正方形.
∴BD=
解:
小试牛刀
②如图①,连接AC,BD,
∵AB=BC,AC⊥BD,
∴∠ABD=∠CBD.
又∵BD=BD,
∴△ABD ≌△CBD,
∴AD=CD.
证明:
小试牛刀
(2)如图②,在矩形ABCD 中,AB=5,BC=9,点P
是对角线BD 上一点,且BP=2PD,过点P 作直线
分别交AD,BC 于点E,F,使四边形ABFE 是等
腰直角四边形,求AE 的长.
小试牛刀
(2)若EF 与BC 垂直,则AE≠EF,BF≠EF,AB≠BF,
AB≠AE,
∴四边形ABFE不是等腰直角四边形,不符合条件.
若EF 与BC 不垂直.
①当AE=AB=5时,如
图②,此时四边形
ABFE 是等腰直角四
边形.
解:
小试牛刀
②当BF=AB 时,如图③,
此时四边形ABFE 是等腰直角四边形.
∴BF=AB=5.
∵DE∥BF,
∴△PED∽△PFB,
∴DE:BF=PD:PB=1:2,
∴DE=2.5,
∴AE=9-2.5=6.5.
综上所述,AE 的长为5或6.5.
小试牛刀
6
如图,在等腰三角形ABC 中,∠ACB=90°,AC=BC=4,D 是AB 的中点,E,F 分别是AC,BC 上的点(点E 不与端点A,C 重合),且AE=CF,连接EF 并取EF 的中点O,连接DO 并延长至点G,使GO=DO,连接DE,DF,GE,GF.
(1)求证:四边形EDFG 是正方形;
(2)当点E 在什么位置时,四边形EDFG 的面积最小?
并求四边形EDFG 面积的最小值.
小试牛刀
(1)如图,连接CD.∵O 是EF 的中点,∴OE=OF.
又∵OD=OG,∴四边形EDFG 为平行四边形.
∵AC=BC,D 为AB 的中点,∠ACB=90°,
∴AD=DC,∠A=∠FCD=45°,CD⊥AB.
在△AED 和△CFD 中,AE=CF,∠A=∠FCD,
AD=DC,∴△AED ≌△CFD.
∴DE=DF,∠ADE=∠CDF.
∴四边形EDFG 为菱形.
∵CD⊥AD,∴∠ADE+∠EDC=90°.
∴∠EDC+∠CDF=90°,即∠EDF=90°.
∴四边形EDFG 为正方形.
证明:
小试牛刀
(2)∵四边形EDFG 为正方形,
∴当正方形EDFG 的边长DE 最短时,其面积最小.
∵垂线段最短,
∴当DE⊥AC 时,四边形EDFG 的面积最小.
∵AD=DC,DE⊥AC,
∴AE=EC,DE= AC=2.
∴当E 为AC 的中点时,四边形EDFG 的面积最小,
四边形EDFG 的面积的最小值=22=4.
解:
课堂小结
课堂小结
1. 判定方法:
(1)从四边形出发:①有四条边相等,四个角都是直角
的四边形是正方形;②对角线互相平分、垂直且相
等的四边形是正方形;
(2)从平行四边形出发:①有一组邻边相等并且有一个
角是直角的平行四边形是正方形;②对角线互相垂
直且相等的平行四边形是正方形;
课堂小结
(3)从矩形出发:
①有一组邻边相等的矩形是正方形;
②对角线互相垂直的矩形是正方形;
(4)从菱形出发:
①有一个角是直角的菱形是正方形;
②对角线相等的菱形是正方形.
2. 四边形间的关系:
(1)平行四边形、矩形、菱形、
正方形间的包含关系如图.
课堂小结
(2)四边形、平行四边形、矩形、菱形、正方形间的转
化关系如图:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.6 正方形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
相传,上古神话人物伏羲在黄河边行走,得到龙马送来的“河图”(如下图所示),在洛水边又得到神龟送来的“洛书”.“河图”、“洛书”是几千年前的两幅图象,是正方形的图案,由点和线交织而成,充满了巧妙的数字关系,说明中华祖先很早对于几何和代数的研究. 充分显示了中华祖先的聪明才智.
新课精讲
探索新知
1
知识点
正方形的对称性
O
A
B
C
D
(A)
(B)
(C)
(D)
正方形的对称性:
正方形是中心对称图形,对称中心为点O;
又是轴对称图形,有四条对称轴.
探索新知
例1 如图,点E 在正方形ABCD 的对角线AC上,且EC
=2AE,直角三角形FEG 的两直角边EF、EG 分别
交BC、DC 于点M、N.若正方形ABCD 的边长为a,
则重叠部分四边形EMCN 的面积为( )
A. a 2 B. a 2
C. a 2 D. a 2
D
探索新知
作EP⊥BC 于点P,EQ⊥CD 于点Q,易得△EPM ≌△EQN,利用四边形EMCN 的面积等于正方形PCQE 的面积求解.
作EP⊥BC 于点P,EQ⊥CD 于点Q,
∵四边形ABCD 是正方形,∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG 是直角三角形,∴∠NEF=∠NEQ+∠MEQ=90°,∴∠PEM=∠NEQ,
∵CA 是∠BCD 的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE 是正方形,
导引:
探索新知
在△EPM 和△EQN 中,
∴△EPM ≌△EQN (ASA),∴S△EQN=S△EPM,
∴四边形EMCN 的面积等于正方形PCQE 的面积,
∵正方形ABCD 的边长为a,∴AC= a,
∵EC=2AE,∴EC= a,∴EP=PC= a,
∴正方形PCQE 的面积= a× a= a 2,
∴四边形EMCN 的面积= a 2.
探索新知
总 结
本例解法在于巧用割补法,将分散的图形拼合在
一起,将不规则的阴影面积集中到一个规则的图形中,
再利用正方形及三角形的性质求出,解答过程体现了
割补法及转化思想.
典题精讲
已知:如图,正方形ABCD 的两条对角线相交于点O,点M,N 分别在OA,OD上,且MN∥AD.请探究线段DM 和CN 之间的数量关系, 写出结论并给出证明.
1
典题精讲
DM=CN.
证明:∵四边形ABCD 是正方形,
∴OA=OD,AD=DC,∠DAM=∠CDN=45°.
又∵MN∥AD,
∴OM=ON.∴AM=DN.
∴△AMD ≌△DNC.
∴DM=CN.
解:
典题精讲
已知:如图,正方形ABCD 的两条对角线相交于点O,E 为OC上一点, AM⊥BE,垂足为M,AM 与DB 相交于点F. 求证:OE=OF.
2
典题精讲
在正方形ABCD 中,OA=OB,
∠BOC=∠AOF=90°.
∵在Rt△AME 中,∠EAM+∠AEM=90°,
在Rt△AOF 中,∠FAO+∠AFO=90°,
∴∠AEM=∠AFO.
∴△AOF ≌△BOE.
∴OE=OF.
证明:
典题精讲
3
如图,菱形ABCD 的面积为120 cm2,正方形AECF 的面积为50 cm2,则菱形的边长为________.
13cm
典题精讲
4
小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )
A.1次 B.2次
C.3次 D.4次
B
探索新知
2
知识点
正方形的判定
思考
正方形有哪些性质?如何判定一个四边形是正方形?
把它们写出来, 并和同学交流一下,然后证明其中的
一些结论.
探索新知
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
探索新知
归 纳
正方形的判定方法:要判定一个四边形是正方形,最
常用的方法就是先证明它是菱形(或矩形),再证明这
个菱形(或矩形)有一个角是直角(或有一组邻边相等),
其实质就是根据正方形的定义来判定,当然也可以先
证四边形是平行四边形,再证有一组邻边相等且有一
个角是直角,或证这个平行四边形的对角线相等并且
互相垂直.
探索新知
例2 如图,△ABC 中,AB=AC,AD 是△ABC 的角平分线,点O 为AB 的中点,连接DO 并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD 是矩形.
(2)当△ABC 满足什么条件时,矩形AEBD 是正方形?并说明理由.
探索新知
(1)利用平行四边形的判定方法首先得出四边形
AEBD 是平行四边形,进而由等腰三角形的
性质得出∠ADB=90°,即可证得结论;
(2)利用等腰直角三角形的性质得出AD=BD=
CD,进而利用正方形的判定方法即可判定
矩形AEBD 是正方形.
导引:
探索新知
(1)证明:∵点O 为AB 的中点,OE=OD,
∴四边形AEBD 是平行四边形.
∵AB=AC,AD 是△ABC 的角平分线,
∴AD⊥BC.∴∠ADB=90°.
∴平行四边形AEBD 是矩形.
(2)解:当∠BAC=90°时,矩形AEBD 是正方形.
理由:∵∠BAC=90°,AB=AC,AD 是△ABC
的角平分线,∴AD=BD=CD.
∵由(1)得四边形AEBD 是矩形,
∴矩形AEBD 是正方形.
探索新知
总 结
本题运用演绎推理解答,(1)中根据对角线互相平
分判定四边形AEBD是平行四边形,再由等腰三角形
三线合一的性质证直角,从而判定四边形AEBD是矩
形.(2)中添加条件后可证得矩形的一组邻边相等,即
可判定该矩形是正方形.
探索新知
例3 如图,已知在 ABCD 中,对角线AC,BD 交于点O,E
是BD 的延长线上的点,且EA=EC.
(1)求证:四边形ABCD 是菱形;
(2)若∠DAC=∠EAD+∠AED,
求证:四边形ABCD 是正方形.
要证 ABCD 是正方形,有三种途径可走:即在平行四
边形、菱形、矩形的基础上,找各需补充的对角线的
条件进行证明;若要证明 ABCD 是菱形,由于题中条
件与对角线相关,则需证AC⊥BD.
导引:
探索新知
(1)首先根据平行四边形的性质可得AO=CO,再由EA
=EC 可得△EAC 是等腰三角形,然后根据等腰三角
形三线合一的性质可得EO⊥AC,根据对角线互相
垂直的平行四边形是菱形可证出结论;
(2)首先根据角的关系得出AO=DO,进而得到AC=
BD,再根据对角线相等的菱形是正方形可得到结论.
探索新知
(1)∵四边形ABCD 是平行四边形,∴AO=CO,
∵EA=EC,∴EO⊥AC,即BD⊥AC,
∴四边形ABCD 是菱形.
(2)∵∠ADO=∠EAD+∠AED,
∠DAC=∠EAD+∠AED,
∴∠ADO=∠DAC,∴AO=DO,
∵四边形ABCD 是菱形,
∴AC=2AO,BD=2DO,
∴AC=BD,∴四边形ABCD 是正方形.
证明:
探索新知
总 结
证明条件中含对角线的四边形是正方形的方法:
(1)证:“四边形+对角线互相垂直、平分且相等”;
(2)证:“平行四边形+对角线互相垂直且相等”;
(3)证:“矩形+对角线互相垂直”;
(4)证:“菱形+对角线相等”.
典题精讲
1 如图,把一张矩形纸片折叠,把重叠部分剪下来,展开后可以得到一个怎样的四边形?为什么?
正方形.因为有三个角是直角,
所以是矩形,由折叠可知一组邻边相等,所以是正方形.
解:
典题精讲
2
如图,在菱形ABCD 中,对角线AC,BD 相交于点O,不添加任何辅助线,请添加一个条件___________________________,使四边形ABCD是正方形.
∠BAD=90°(答案不唯一)
典题精讲
3
下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且互相平分的四边形是正方形
D
典题精讲
4
关于 ABCD 的叙述,正确的是( )
A.若AB⊥BC,则 ABCD 是菱形
B.若AC⊥BD,则 ABCD 是正方形
C.若AC=BD,则 ABCD 是矩形
D.若AB=AD,则 ABCD 是正方形
C
典题精讲
5
小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD 中选两个作为补充条件,使 ABCD 为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①②
B.②③
C.①③
D.②④
B
易错提醒
四边形ABCD 的对角线AC 和BD 相交于点O,假设有下列条件:①AB=AD; ②∠DAB=90°;
③AO=CO,BO=DO; ④四边形ABCD 为矩形;
⑤四边形ABCD 为菱形; ⑥四边形ABCD 为正方形.
则下列推理不成立的是( )
A.①④ ⑥ B.①③ ⑤
C.①② ⑥ D.②③ ④
易错点:将特殊四边形的判定相混淆导致出错
C
学以致用
小试牛刀
将五个边长都为2 cm的正方形按如图所示方式摆放,点A,B,C,D 分别是四个正方形的中心,则图中四块阴影部分面积的和为( )
A.2 cm2
B.4 cm2
C.6 cm2
D.8 cm2
B
1
小试牛刀
在△ABC 中,点D,E,F 分别在BC,AB,CA上,且DE∥CA,DF∥BA,连接EF,AD,则下列三种说法:
①如果EF=AD,那么四边形AEDF 是矩形;
②如果EF⊥AD,那么四边形AEDF 是菱形;
③如果AD⊥BC 且AB=AC,那么四边形AEDF 是正方形,其中正确的有( )
A.3个 B.2个
C.1个 D.0个
B
2
小试牛刀
3
已知:如图,在菱形ABCD 中,点E,O,F 分别为AB,AC,AD 的中点,连接CE,CF,OE,OF.
(1)求证:△BCE ≌△DCF.
(2)当AB 与BC 满足什么关系时,四边形AEOF 是正方形?请说明理由.
小试牛刀
(1)∵四边形ABCD 是菱形,
∴AB=BC=CD=DA,∠B=∠D.
∵点E,F 分别为AB,AD 的中点,
∴BE= AB,DF= AD.
∴BE=DF.
在△BCE 和△DCF 中,
∴△BCE ≌△DCF (SAS).
证明:
小试牛刀
(2)AB⊥BC,理由如下:
∵点E,O,F 分别为AB,AC,AD 的中点,
∴OE= BC= AD=AF.
同理可证:OF=AE= AB;
∴OE=OF=AF=AE.
∴四边形AEOF 是菱形.
∵AB⊥BC,又易知OE∥BC,∴AE⊥OE.
∴四边形AEOF 是正方形.
解:
小试牛刀
4
如图,已知在△ABC 中,AB=AC,D 为BC 边的中点,过点D 作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED ≌△CFD;
(2)若∠A=90°,求证:四边形DFAE 是正方形.
小试牛刀
(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D 是BC 的中点,∴BD=CD.
∴△BED ≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
∵∠A=90°,∴四边形DFAE 为矩形.
∵△BED ≌△CFD,∴DE=DF.
∴四边形DFAE 是正方形.
证明:
小试牛刀
5
定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图①,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD 的长.
②若AC⊥BD,
求证:AD=CD.
小试牛刀
(1)①∵AB=CD=1,AB∥CD,
∴四边形ABCD 是平行四边形.
又∵AB=BC,
∴四边形ABCD 是菱形.
又∵∠ABC=90°,
∴四边形ABCD 是正方形.
∴BD=
解:
小试牛刀
②如图①,连接AC,BD,
∵AB=BC,AC⊥BD,
∴∠ABD=∠CBD.
又∵BD=BD,
∴△ABD ≌△CBD,
∴AD=CD.
证明:
小试牛刀
(2)如图②,在矩形ABCD 中,AB=5,BC=9,点P
是对角线BD 上一点,且BP=2PD,过点P 作直线
分别交AD,BC 于点E,F,使四边形ABFE 是等
腰直角四边形,求AE 的长.
小试牛刀
(2)若EF 与BC 垂直,则AE≠EF,BF≠EF,AB≠BF,
AB≠AE,
∴四边形ABFE不是等腰直角四边形,不符合条件.
若EF 与BC 不垂直.
①当AE=AB=5时,如
图②,此时四边形
ABFE 是等腰直角四
边形.
解:
小试牛刀
②当BF=AB 时,如图③,
此时四边形ABFE 是等腰直角四边形.
∴BF=AB=5.
∵DE∥BF,
∴△PED∽△PFB,
∴DE:BF=PD:PB=1:2,
∴DE=2.5,
∴AE=9-2.5=6.5.
综上所述,AE 的长为5或6.5.
小试牛刀
6
如图,在等腰三角形ABC 中,∠ACB=90°,AC=BC=4,D 是AB 的中点,E,F 分别是AC,BC 上的点(点E 不与端点A,C 重合),且AE=CF,连接EF 并取EF 的中点O,连接DO 并延长至点G,使GO=DO,连接DE,DF,GE,GF.
(1)求证:四边形EDFG 是正方形;
(2)当点E 在什么位置时,四边形EDFG 的面积最小?
并求四边形EDFG 面积的最小值.
小试牛刀
(1)如图,连接CD.∵O 是EF 的中点,∴OE=OF.
又∵OD=OG,∴四边形EDFG 为平行四边形.
∵AC=BC,D 为AB 的中点,∠ACB=90°,
∴AD=DC,∠A=∠FCD=45°,CD⊥AB.
在△AED 和△CFD 中,AE=CF,∠A=∠FCD,
AD=DC,∴△AED ≌△CFD.
∴DE=DF,∠ADE=∠CDF.
∴四边形EDFG 为菱形.
∵CD⊥AD,∴∠ADE+∠EDC=90°.
∴∠EDC+∠CDF=90°,即∠EDF=90°.
∴四边形EDFG 为正方形.
证明:
小试牛刀
(2)∵四边形EDFG 为正方形,
∴当正方形EDFG 的边长DE 最短时,其面积最小.
∵垂线段最短,
∴当DE⊥AC 时,四边形EDFG 的面积最小.
∵AD=DC,DE⊥AC,
∴AE=EC,DE= AC=2.
∴当E 为AC 的中点时,四边形EDFG 的面积最小,
四边形EDFG 的面积的最小值=22=4.
解:
课堂小结
课堂小结
1. 判定方法:
(1)从四边形出发:①有四条边相等,四个角都是直角
的四边形是正方形;②对角线互相平分、垂直且相
等的四边形是正方形;
(2)从平行四边形出发:①有一组邻边相等并且有一个
角是直角的平行四边形是正方形;②对角线互相垂
直且相等的平行四边形是正方形;
课堂小结
(3)从矩形出发:
①有一组邻边相等的矩形是正方形;
②对角线互相垂直的矩形是正方形;
(4)从菱形出发:
①有一个角是直角的菱形是正方形;
②对角线相等的菱形是正方形.
2. 四边形间的关系:
(1)平行四边形、矩形、菱形、
正方形间的包含关系如图.
课堂小结
(2)四边形、平行四边形、矩形、菱形、正方形间的转
化关系如图:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
