【班海精品】冀教版(新)八下-22.7 多边形的内角和与外角和【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-22.7 多边形的内角和与外角和【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览










文档简介
(共63张PPT)
22.7 多边形的内角和与外角和
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
情景导入
看一看
情景导入
小明有一个设想:
2022年世界杯在卡塔尔举行,要是能设计一个内
角和是2022°的多边形花坛该多有意义啊!小明的这
个想法能实现吗?
新课精讲
探索新知
1
知识点
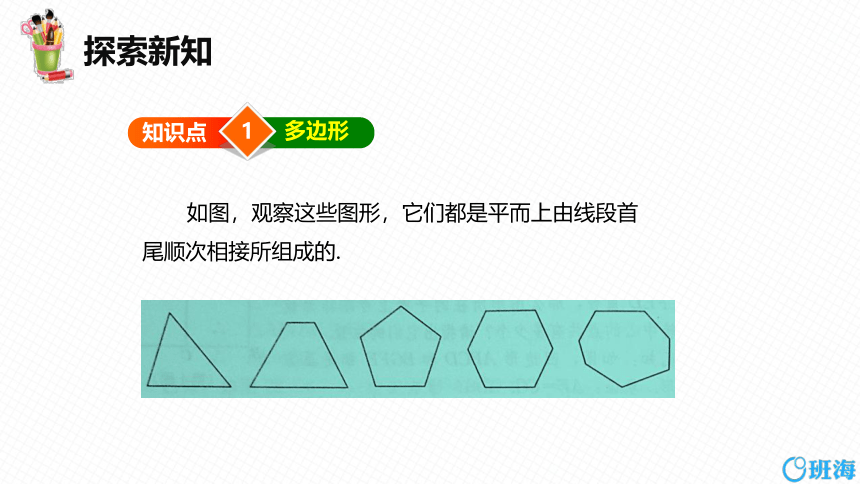
多边形
如图,观察这些图形,它们都是平而上由线段首
尾顺次相接所组成的.
探索新知
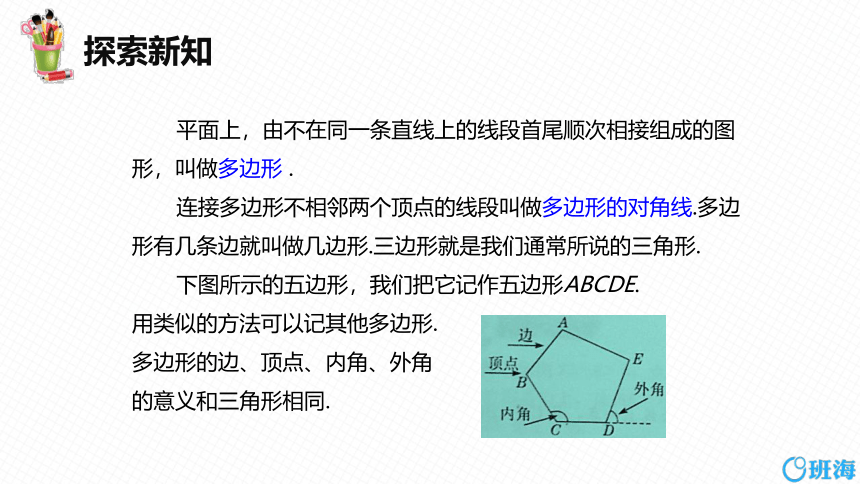
平面上,由不在同一条直线上的线段首尾顺次相接组成的图形,叫做多边形 .
连接多边形不相邻两个顶点的线段叫做多边形的对角线.多边形有几条边就叫做几边形.三边形就是我们通常所说的三角形.
下图所示的五边形,我们把它记作五边形ABCDE.
用类似的方法可以记其他多边形.
多边形的边、顶点、内角、外角
的意义和三角形相同.
探索新知
例1 下列说法中,正确的有( )
(1)三角形是边数最少的多边形;
(2)由n 条线段连接起来组成的图形叫多边形;
(3)n 边形有n 条边、n 个顶点、2n 个内角和外角;
(4)多边形分为凹多边形和凸多边形.
A.1个 B.2个
C.3个 D.4个
B
探索新知
(2)的说法不严密,应点明三点:其一,“不在同
一条直线上”的线段;其二,是“平面图形”;
其三,“线段首尾顺次相接”;
(3)n 边形有n 个内角和2n 个外角,即外角的个数是
内角个数的2倍.
(1)(4)说法正确.
导引:
探索新知
总 结
(1)理解多边形的定义,要从多边形的几个条件入手.
(2)一个n 边形,它的顶点数、内角的个数都是n 个,
只有外角有2n 个.
典题精讲
下列图形中,不是多边形的是( )
从六边形的一个顶点出发,可以画出m 条对角线,它们将六边形分成n 个三角形,则m、n 的值分别为( )
A.4、3 B.3、3
C.3、4 D.4、4
1
C
2
C
探索新知
2
知识点
多边形的内角和
在纸上任意画一个四边形,剪下它的四个角,
把它们拼在起(四个角的顶点里合).你发现了什么?
其他同学与你的发现相同吗?你能把你的发现概括
成一个命题吗?你能证明这个命题吗?
探索新知
四边形有以下的定理:
四边形的内角和等于360°.
已知:四边形ABCD.
求证: ∠A+∠B+∠C+∠D=360°.
证明 如图,连接BD.
∵∠A+∠ABD+∠ADB=180°,
∠C+∠CBD+∠CDB=180°.
∴∠A+∠ABD+∠ADB+ ∠C+∠CBD+∠CDB
=180°+180°=360°,
即∠A+∠ABC+∠C+∠CDA=360°.
A
B
C
D
探索新知
边数 图形 从某顶点出发的对角线条数 划分成的三角形个数 多边形的内角和
3 0 1 1×180°
4 1 2 2×180°
5
6
… … … … …
n
探索新知
归 纳
对于n 边形,从某一个顶点出发的(n -3)条对角线
把n 边形划分成 (n-2)个三角形,所以n 边形的内角和
就等于这(n -2)个三角形的所有内角之和.于是就有下
面的定理:
n 边形的内角和为(n -2)×180°(n≥3).
探索新知
例2 一个六边形如图1.已知AB∥DE,BC∥EF,CD∥AF.求∠A+∠C+∠E 的值.
因为两条平行线被一条直线所
截.有许多等角关系,所以我们
不妨连结AD 试试看,如图2.不
难发现,∠1=∠3,∠2=∠4.由
此可得本题解法.
分析:
图1
图2
探索新知
如图2,连结AD.
∵AB∥DE,CD∥AF (已知),
∴∠1=∠3,∠2=∠4.
∴∠1+∠2=∠3+∠4.即∠FAB=∠CDE.
同理,∠B=∠E,∠C=∠F.
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2)×180°=720°.
∴∠FAB+∠C+∠E= ×720°=360°.
解:
图2
探索新知
总 结
把多边形的内角和的问题转化为四边形内角和、
三角形内角和问题是常用的解题思路.
典题精讲
在540°,720°,960°中,哪个角度不可能是多边形的内角和?
在四边形ABCD 中,如果∠A+∠C+∠D=280°,那么∠B 的度数是多少?
解: 960°不可能是多边形的内角和.
解: ∠B=360°-(∠A+∠C+∠D)
=360°-280°=80°.
典题精讲
一个五边形有三个内角是直角,另两个内角都等于n°.求n 的值.
过某个多边形一个顶点的对角线有10条.求这个多边形的内角和.
解:由题意可知90°×3+2n°=(5-2)×180°.
解得n=135.
解:设这个多边形的边数为n,则n-3=10,
∴n=13.∴内角和为(13-2)×180°=1 980°.
典题精讲
5 四边形的四个内角可以都是锐角吗,可以都是钝角吗?为什么?
解:不可以.四边形的内角和是360°,如果四边形的四个内角都是锐角,那么它的内角和小于360°;如果都是钝角,那么它的内角和大于360°.
探索新知
例3 若一个多边形的内角和是900°,则这个多边形是( )
A.五边形 B.六边形
C.七边形 D.八边形
设这个多边形的边数为n,由题意得(n-2)×
180°=900°,解得:n=7.
导引:
C
探索新知
总 结
已知多边形的内角和求边数n 的方法:根据多边
形内角和公式:(n-2)×180°=内角和列方程,解
方程求出n 的值,即得多边形的边数.
典题精讲
1 一个多边形的内角和等于1 080°,这个多边形的边数是多少?
解:设这个多边形的边数为n.
则(n-2)×180°=1 080°. 解得n=8.
∴这个多边形的边数为8.
解: ∠D= ×360°=144°.
在四边形ABCD 中,已知∠A:∠B :∠C :∠D=
1:2:3:4.求∠D 的度数.
典题精讲
内角和为540°的多边形是( )
3
C
典题精讲
如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①② B.①③
C.②④ D.③④
4
B
典题精讲
将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540°
C.720° D.900°
5
D
典题精讲
将一个n 边形变成(n+1)边形,内角和将( )
A.减少180° B.增加90°
C.增加180° D.增加360°
一个多边形除一个内角外其余内角的和为
1 510°,则这个多边形对角线的条数是( )
A.27 B.35
C.44 D.54
6
C
7
C
探索新知
3
知识点
多边形的外角和
由于每一个外角与和它相邻的内角互补,
所以n 边形的外角和(每一个顶点只取一个外角)为
n×180°-(n-2)×180°= 360°.
任何多边形的外角和为360°.
探索新知
定理:多边形的外角和等于360°.
要点精析
(1)多边形的外角和与多边形的边数无关,它始终为360°;
(2)若n 边形的每个内角相等,则每一个外角的度数
为 (n≥3).
探索新知
例4 已知一个多边形的每个外角都等于40°,则这个多边形是( )
A.五边形 B.九边形
C.七边形 D.八边形
根据多边形外角和等于360°,直接可求出多边
形的边数.
导引:
B
探索新知
总 结
用多边形外角和定理求多边形内(外)角的度数或
求多边形的边数的方法:一般可利用方程思想通过
列方程解决,本例根据边数× 多边形每个外角的度
数=360°,即可求出.
典题精讲
1 如图所示的模板,规定:AB,CD 的延长线应相交成80°的角.因交点不在板上,不便测量,工人师傅测得∠BAE=122°,∠OCF=155°.此时AB,CD 的延长线相交所成的角是否符合规定 为什么
不符合规定.理由:因为五边形
AEFCG 的内角和为(5-2)×180°
=540°.所以∠AGC=540°-(∠E
+∠F+∠BAE+∠DCF)=540°
-457°=83°≠80°.所以不符合规定.
解:
典题精讲
五边形的外角和等于( )
A.180° B.360°
C.540° D.720°
如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°……照这样走下去,他第一次回到出发地点A时,一共走的路程是( )
A.140米 B.150米
C.160米 D.240米
2
B
3
B
探索新知
4
知识点
多边形内角和与外角和的关系
例5 一个多边形的内角和是外角和的3倍,则这个多边形的边数是________.
设这个多边形的边数为n,
∵多边形的外角和为360°,
∴(n-2)×180°=3×360°.
解得:n=8.
导引:
8
探索新知
总 结
因为多边形的外角和是定值,所以有些多边形
的问题经常转化为外角的问题来解决. 多边形的内角
和、外角和在应用时注意区分,不要混了.
典题精讲
内角和等于外角和的2倍的多边形是几边形?
一个n 边形的外角和与内角和的度数之比为2:7.
求n 的值.
解:设这个多边形的边数为n,则(n-2)·180°=2×360°.解得n=6.所以这个多边形是六边形.
解:由题意可知 ,
所以n=9.
典题精讲
3 如图,在四边形ABCD 中,∠A=∠C=90°,BE 平分∠ABC,DF 平分∠ADC. BE 与DF 有怎样的位置关系?为什么?
典题精讲
解:BE∥DF.理由:∵∠A=∠C=90°,
∴∠ADC+∠ABC=360°-(∠A+∠C)=180°.
∵BE,DF 分别平分∠ABC,∠ADC,
∴∠ABE= ∠ABC,∠ADF= ∠ADC.
∴∠ABE+∠ADF= ∠ABC+ ∠ADC
= ×180°=90°.
又易知∠ABE+∠AEB=90°,
∴∠AEB=∠ADF.∴BE∥DF.
典题精讲
已知一个多边形的内角和等于它的外角和,则这个多边形的边数为( )
A.3 B.4
C.5 D.6
一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形
C.六边形 D.八边形
4
B
5
C
易错提醒
已知多边形的一个外角与除该外角对应的内角外的其余各内角的和为600°,求该外角的度数.
解:设多边形的边数为n,这个外角的度数为x °,
则与这个外角相邻的内角为(180-x )°.
由题意,得(n-2)×180+x-(180-x )=600,
解得x=570-90n.
易错提醒
∵0又∵n 为整数,∴n=5或n=6.
∴当边数为5时,该外角为120°;
当边数为6时,该外角为30°.
易错点:忽视角的度数的取值范围
学以致用
小试牛刀
从一个n 边形的同一个顶点出发,分别连接这个顶点和与它不相邻的各顶点,若把这个多边形分割成6个三角形,则n 的值是( )
A.6 B.7
C.8 D.9
C
1
小试牛刀
一个多边形截去一个角后,形成一个新多边形的内角和是1 620°,则原来多边形的边数是( )
A.10 B.11
C.12 D.以上都有可能
D
2
小试牛刀
设四边形的内角和等于a,五边形的外角和等于b,则a 与b 的关系是( )
A.a>b B.a=b
C.a<b D.b=a+180°
B
3
小试牛刀
一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )
A.12 B.13
C.14 D.15
C
4
小试牛刀
5
已知n 边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ 能取360°;而乙同学说,θ 也能取
630°.甲、乙的说法对吗?若对,求出边数n. 若
不对,说明理由.
(2)若n 边形变为(n+x )边形,发现内角和增加了360°,
用列方程的方法确定x.
小试牛刀
(1)甲的说法对,乙的说法不对.
θ=360°时,(n-2)×180=360. 解得n=4.
θ=630°时,(n-2)×180=630,解得n= ,
与n 为整数不符,
∴θ 不能取630°.
(2)依题意,
得(n-2)×180°+360°=(n+x-2)×180°.
解得x=2.
解:
小试牛刀
6
观察图中的图形,并回答问题.
(1)四边形、五边形、六边形各有几条对角线?从
中得到什么规律?
(2)根据规律求七边形的对角线的条数.
(3)n 边形的对角线的条数呢?
小试牛刀
(1)四边形有2条对角线,五边形有5条对角线,
六边形有9条对角线.
2= ,5= ,9=
(2)七边形的对角线有 =14(条).
(3)n 边形的对角线有 条.
解:
小试牛刀
7
如图,六边形ABCDEF 的六个内角都相等,若AB=1,BC=CD=3,DE=2,则这个六边形的周长是多少?
小试牛刀
如图,分别作直线AB,CD,EF 的延长线和反向延长线使它们交于点G,P,H.
∵六边形ABCDEF 的六个内角都相等,
∴六个内角都是120°.
∴六边形ABCDEF 的每一个外角的都是60°.
∴△AHF,△BGC,△DPE,
△GHP 都是等边三角形.
解:
小试牛刀
∴GC=BC=3,DP=DE=PE=2,AH=HF=AF.
∴GH=HP=GP=GC+CD+DP=3+3+2=8,
∴HF=FA=HA=GH-AB-BG=8-1-3=4.
∴EF=PH-HF-EP=8-4-2=2.
∴六边形的周长是1+3+3+2+2+4=15.
小试牛刀
(1)如图①②,试探究其中∠1,∠2与∠3,∠4之
间的数量关系;
(2)请你用文字描述上述的关系;
8
小试牛刀
(1)设∠1的邻补角为∠5,∠2的邻补角为∠6.
∵∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)在四边形中,两个外角的和等于与它们不相邻
的两个内角的和.
解:
小试牛刀
(3)用你发现的结论解决下面的问题:
如图③,AE,DE 分别是四边形ABCD 的外角
∠NAD,∠MDA 的平分线,∠B+∠C=240°,
求∠E 的度数.
小试牛刀
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE,DE 分别是∠NAD,∠MDA 的平分线,
∴∠ADE= ∠MDA,∠DAE= ∠NAD.
∴∠ADE+∠DAE= (∠MDA+∠NAD )
=120°.
∴∠E=180°-(∠ADE+∠DAE )=60°.
解:
课堂小结
课堂小结
定义:平面上,由不在同一条直线上的线段首尾顺次
相接组成的图形叫做多边形。
n 边形的内角和为(n-2)×180°(n≥3).
n 边形一个顶点出发可引(n-3)条对角线.
则n 个顶点的n 边形共有 条对角线.
多边形的外角和等于360°.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
22.7 多边形的内角和与外角和
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
情景导入
看一看
情景导入
小明有一个设想:
2022年世界杯在卡塔尔举行,要是能设计一个内
角和是2022°的多边形花坛该多有意义啊!小明的这
个想法能实现吗?
新课精讲
探索新知
1
知识点
多边形
如图,观察这些图形,它们都是平而上由线段首
尾顺次相接所组成的.
探索新知
平面上,由不在同一条直线上的线段首尾顺次相接组成的图形,叫做多边形 .
连接多边形不相邻两个顶点的线段叫做多边形的对角线.多边形有几条边就叫做几边形.三边形就是我们通常所说的三角形.
下图所示的五边形,我们把它记作五边形ABCDE.
用类似的方法可以记其他多边形.
多边形的边、顶点、内角、外角
的意义和三角形相同.
探索新知
例1 下列说法中,正确的有( )
(1)三角形是边数最少的多边形;
(2)由n 条线段连接起来组成的图形叫多边形;
(3)n 边形有n 条边、n 个顶点、2n 个内角和外角;
(4)多边形分为凹多边形和凸多边形.
A.1个 B.2个
C.3个 D.4个
B
探索新知
(2)的说法不严密,应点明三点:其一,“不在同
一条直线上”的线段;其二,是“平面图形”;
其三,“线段首尾顺次相接”;
(3)n 边形有n 个内角和2n 个外角,即外角的个数是
内角个数的2倍.
(1)(4)说法正确.
导引:
探索新知
总 结
(1)理解多边形的定义,要从多边形的几个条件入手.
(2)一个n 边形,它的顶点数、内角的个数都是n 个,
只有外角有2n 个.
典题精讲
下列图形中,不是多边形的是( )
从六边形的一个顶点出发,可以画出m 条对角线,它们将六边形分成n 个三角形,则m、n 的值分别为( )
A.4、3 B.3、3
C.3、4 D.4、4
1
C
2
C
探索新知
2
知识点
多边形的内角和
在纸上任意画一个四边形,剪下它的四个角,
把它们拼在起(四个角的顶点里合).你发现了什么?
其他同学与你的发现相同吗?你能把你的发现概括
成一个命题吗?你能证明这个命题吗?
探索新知
四边形有以下的定理:
四边形的内角和等于360°.
已知:四边形ABCD.
求证: ∠A+∠B+∠C+∠D=360°.
证明 如图,连接BD.
∵∠A+∠ABD+∠ADB=180°,
∠C+∠CBD+∠CDB=180°.
∴∠A+∠ABD+∠ADB+ ∠C+∠CBD+∠CDB
=180°+180°=360°,
即∠A+∠ABC+∠C+∠CDA=360°.
A
B
C
D
探索新知
边数 图形 从某顶点出发的对角线条数 划分成的三角形个数 多边形的内角和
3 0 1 1×180°
4 1 2 2×180°
5
6
… … … … …
n
探索新知
归 纳
对于n 边形,从某一个顶点出发的(n -3)条对角线
把n 边形划分成 (n-2)个三角形,所以n 边形的内角和
就等于这(n -2)个三角形的所有内角之和.于是就有下
面的定理:
n 边形的内角和为(n -2)×180°(n≥3).
探索新知
例2 一个六边形如图1.已知AB∥DE,BC∥EF,CD∥AF.求∠A+∠C+∠E 的值.
因为两条平行线被一条直线所
截.有许多等角关系,所以我们
不妨连结AD 试试看,如图2.不
难发现,∠1=∠3,∠2=∠4.由
此可得本题解法.
分析:
图1
图2
探索新知
如图2,连结AD.
∵AB∥DE,CD∥AF (已知),
∴∠1=∠3,∠2=∠4.
∴∠1+∠2=∠3+∠4.即∠FAB=∠CDE.
同理,∠B=∠E,∠C=∠F.
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2)×180°=720°.
∴∠FAB+∠C+∠E= ×720°=360°.
解:
图2
探索新知
总 结
把多边形的内角和的问题转化为四边形内角和、
三角形内角和问题是常用的解题思路.
典题精讲
在540°,720°,960°中,哪个角度不可能是多边形的内角和?
在四边形ABCD 中,如果∠A+∠C+∠D=280°,那么∠B 的度数是多少?
解: 960°不可能是多边形的内角和.
解: ∠B=360°-(∠A+∠C+∠D)
=360°-280°=80°.
典题精讲
一个五边形有三个内角是直角,另两个内角都等于n°.求n 的值.
过某个多边形一个顶点的对角线有10条.求这个多边形的内角和.
解:由题意可知90°×3+2n°=(5-2)×180°.
解得n=135.
解:设这个多边形的边数为n,则n-3=10,
∴n=13.∴内角和为(13-2)×180°=1 980°.
典题精讲
5 四边形的四个内角可以都是锐角吗,可以都是钝角吗?为什么?
解:不可以.四边形的内角和是360°,如果四边形的四个内角都是锐角,那么它的内角和小于360°;如果都是钝角,那么它的内角和大于360°.
探索新知
例3 若一个多边形的内角和是900°,则这个多边形是( )
A.五边形 B.六边形
C.七边形 D.八边形
设这个多边形的边数为n,由题意得(n-2)×
180°=900°,解得:n=7.
导引:
C
探索新知
总 结
已知多边形的内角和求边数n 的方法:根据多边
形内角和公式:(n-2)×180°=内角和列方程,解
方程求出n 的值,即得多边形的边数.
典题精讲
1 一个多边形的内角和等于1 080°,这个多边形的边数是多少?
解:设这个多边形的边数为n.
则(n-2)×180°=1 080°. 解得n=8.
∴这个多边形的边数为8.
解: ∠D= ×360°=144°.
在四边形ABCD 中,已知∠A:∠B :∠C :∠D=
1:2:3:4.求∠D 的度数.
典题精讲
内角和为540°的多边形是( )
3
C
典题精讲
如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①② B.①③
C.②④ D.③④
4
B
典题精讲
将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )
A.360° B.540°
C.720° D.900°
5
D
典题精讲
将一个n 边形变成(n+1)边形,内角和将( )
A.减少180° B.增加90°
C.增加180° D.增加360°
一个多边形除一个内角外其余内角的和为
1 510°,则这个多边形对角线的条数是( )
A.27 B.35
C.44 D.54
6
C
7
C
探索新知
3
知识点
多边形的外角和
由于每一个外角与和它相邻的内角互补,
所以n 边形的外角和(每一个顶点只取一个外角)为
n×180°-(n-2)×180°= 360°.
任何多边形的外角和为360°.
探索新知
定理:多边形的外角和等于360°.
要点精析
(1)多边形的外角和与多边形的边数无关,它始终为360°;
(2)若n 边形的每个内角相等,则每一个外角的度数
为 (n≥3).
探索新知
例4 已知一个多边形的每个外角都等于40°,则这个多边形是( )
A.五边形 B.九边形
C.七边形 D.八边形
根据多边形外角和等于360°,直接可求出多边
形的边数.
导引:
B
探索新知
总 结
用多边形外角和定理求多边形内(外)角的度数或
求多边形的边数的方法:一般可利用方程思想通过
列方程解决,本例根据边数× 多边形每个外角的度
数=360°,即可求出.
典题精讲
1 如图所示的模板,规定:AB,CD 的延长线应相交成80°的角.因交点不在板上,不便测量,工人师傅测得∠BAE=122°,∠OCF=155°.此时AB,CD 的延长线相交所成的角是否符合规定 为什么
不符合规定.理由:因为五边形
AEFCG 的内角和为(5-2)×180°
=540°.所以∠AGC=540°-(∠E
+∠F+∠BAE+∠DCF)=540°
-457°=83°≠80°.所以不符合规定.
解:
典题精讲
五边形的外角和等于( )
A.180° B.360°
C.540° D.720°
如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°……照这样走下去,他第一次回到出发地点A时,一共走的路程是( )
A.140米 B.150米
C.160米 D.240米
2
B
3
B
探索新知
4
知识点
多边形内角和与外角和的关系
例5 一个多边形的内角和是外角和的3倍,则这个多边形的边数是________.
设这个多边形的边数为n,
∵多边形的外角和为360°,
∴(n-2)×180°=3×360°.
解得:n=8.
导引:
8
探索新知
总 结
因为多边形的外角和是定值,所以有些多边形
的问题经常转化为外角的问题来解决. 多边形的内角
和、外角和在应用时注意区分,不要混了.
典题精讲
内角和等于外角和的2倍的多边形是几边形?
一个n 边形的外角和与内角和的度数之比为2:7.
求n 的值.
解:设这个多边形的边数为n,则(n-2)·180°=2×360°.解得n=6.所以这个多边形是六边形.
解:由题意可知 ,
所以n=9.
典题精讲
3 如图,在四边形ABCD 中,∠A=∠C=90°,BE 平分∠ABC,DF 平分∠ADC. BE 与DF 有怎样的位置关系?为什么?
典题精讲
解:BE∥DF.理由:∵∠A=∠C=90°,
∴∠ADC+∠ABC=360°-(∠A+∠C)=180°.
∵BE,DF 分别平分∠ABC,∠ADC,
∴∠ABE= ∠ABC,∠ADF= ∠ADC.
∴∠ABE+∠ADF= ∠ABC+ ∠ADC
= ×180°=90°.
又易知∠ABE+∠AEB=90°,
∴∠AEB=∠ADF.∴BE∥DF.
典题精讲
已知一个多边形的内角和等于它的外角和,则这个多边形的边数为( )
A.3 B.4
C.5 D.6
一个多边形的内角和是外角和的2倍,这个多边形是( )
A.四边形 B.五边形
C.六边形 D.八边形
4
B
5
C
易错提醒
已知多边形的一个外角与除该外角对应的内角外的其余各内角的和为600°,求该外角的度数.
解:设多边形的边数为n,这个外角的度数为x °,
则与这个外角相邻的内角为(180-x )°.
由题意,得(n-2)×180+x-(180-x )=600,
解得x=570-90n.
易错提醒
∵0
∴当边数为5时,该外角为120°;
当边数为6时,该外角为30°.
易错点:忽视角的度数的取值范围
学以致用
小试牛刀
从一个n 边形的同一个顶点出发,分别连接这个顶点和与它不相邻的各顶点,若把这个多边形分割成6个三角形,则n 的值是( )
A.6 B.7
C.8 D.9
C
1
小试牛刀
一个多边形截去一个角后,形成一个新多边形的内角和是1 620°,则原来多边形的边数是( )
A.10 B.11
C.12 D.以上都有可能
D
2
小试牛刀
设四边形的内角和等于a,五边形的外角和等于b,则a 与b 的关系是( )
A.a>b B.a=b
C.a<b D.b=a+180°
B
3
小试牛刀
一个多边形的内角和比其外角和的2倍多180°,则该多边形的对角线的条数是( )
A.12 B.13
C.14 D.15
C
4
小试牛刀
5
已知n 边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ 能取360°;而乙同学说,θ 也能取
630°.甲、乙的说法对吗?若对,求出边数n. 若
不对,说明理由.
(2)若n 边形变为(n+x )边形,发现内角和增加了360°,
用列方程的方法确定x.
小试牛刀
(1)甲的说法对,乙的说法不对.
θ=360°时,(n-2)×180=360. 解得n=4.
θ=630°时,(n-2)×180=630,解得n= ,
与n 为整数不符,
∴θ 不能取630°.
(2)依题意,
得(n-2)×180°+360°=(n+x-2)×180°.
解得x=2.
解:
小试牛刀
6
观察图中的图形,并回答问题.
(1)四边形、五边形、六边形各有几条对角线?从
中得到什么规律?
(2)根据规律求七边形的对角线的条数.
(3)n 边形的对角线的条数呢?
小试牛刀
(1)四边形有2条对角线,五边形有5条对角线,
六边形有9条对角线.
2= ,5= ,9=
(2)七边形的对角线有 =14(条).
(3)n 边形的对角线有 条.
解:
小试牛刀
7
如图,六边形ABCDEF 的六个内角都相等,若AB=1,BC=CD=3,DE=2,则这个六边形的周长是多少?
小试牛刀
如图,分别作直线AB,CD,EF 的延长线和反向延长线使它们交于点G,P,H.
∵六边形ABCDEF 的六个内角都相等,
∴六个内角都是120°.
∴六边形ABCDEF 的每一个外角的都是60°.
∴△AHF,△BGC,△DPE,
△GHP 都是等边三角形.
解:
小试牛刀
∴GC=BC=3,DP=DE=PE=2,AH=HF=AF.
∴GH=HP=GP=GC+CD+DP=3+3+2=8,
∴HF=FA=HA=GH-AB-BG=8-1-3=4.
∴EF=PH-HF-EP=8-4-2=2.
∴六边形的周长是1+3+3+2+2+4=15.
小试牛刀
(1)如图①②,试探究其中∠1,∠2与∠3,∠4之
间的数量关系;
(2)请你用文字描述上述的关系;
8
小试牛刀
(1)设∠1的邻补角为∠5,∠2的邻补角为∠6.
∵∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)在四边形中,两个外角的和等于与它们不相邻
的两个内角的和.
解:
小试牛刀
(3)用你发现的结论解决下面的问题:
如图③,AE,DE 分别是四边形ABCD 的外角
∠NAD,∠MDA 的平分线,∠B+∠C=240°,
求∠E 的度数.
小试牛刀
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE,DE 分别是∠NAD,∠MDA 的平分线,
∴∠ADE= ∠MDA,∠DAE= ∠NAD.
∴∠ADE+∠DAE= (∠MDA+∠NAD )
=120°.
∴∠E=180°-(∠ADE+∠DAE )=60°.
解:
课堂小结
课堂小结
定义:平面上,由不在同一条直线上的线段首尾顺次
相接组成的图形叫做多边形。
n 边形的内角和为(n-2)×180°(n≥3).
n 边形一个顶点出发可引(n-3)条对角线.
则n 个顶点的n 边形共有 条对角线.
多边形的外角和等于360°.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
