【班海精品】冀教版(新)八下-19.4 坐标与图形的变化【优质教案】
文档属性
| 名称 | 【班海精品】冀教版(新)八下-19.4 坐标与图形的变化【优质教案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 129.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:20:27 | ||
图片预览


文档简介
班海数学精批——一本可精细批改的教辅
19.4 坐标与图形的变化
用坐标表示平移
一、教学目标
初步掌握点的坐标变化与点的平移关系,进而理解图形各个点的坐标变化与图形平移的关系,并解决与平移有关的问题.
经历探索点的平移与点的坐标变化之间的规律过程,体会数形结合思想. 了解利用图形的平移变换解决简单问题.
培养学生主动探索的精神,提高学生的学习兴趣.
二、教学重点和难点
教学重点是让学生发现并归纳点的坐标变化与点的平移的关系;教学难点是文字语言、图形语言、坐标表示之间的转化以及应用.
三、教学方法和教学手段
本课采用教师的启发引导与学生的自主探究相结合的教学方法,利用多媒体等手段教学.
四、教学过程设计与实施
根据班级学生基础较好的特点,我把这节课分为五个环节:
(一)一起探究
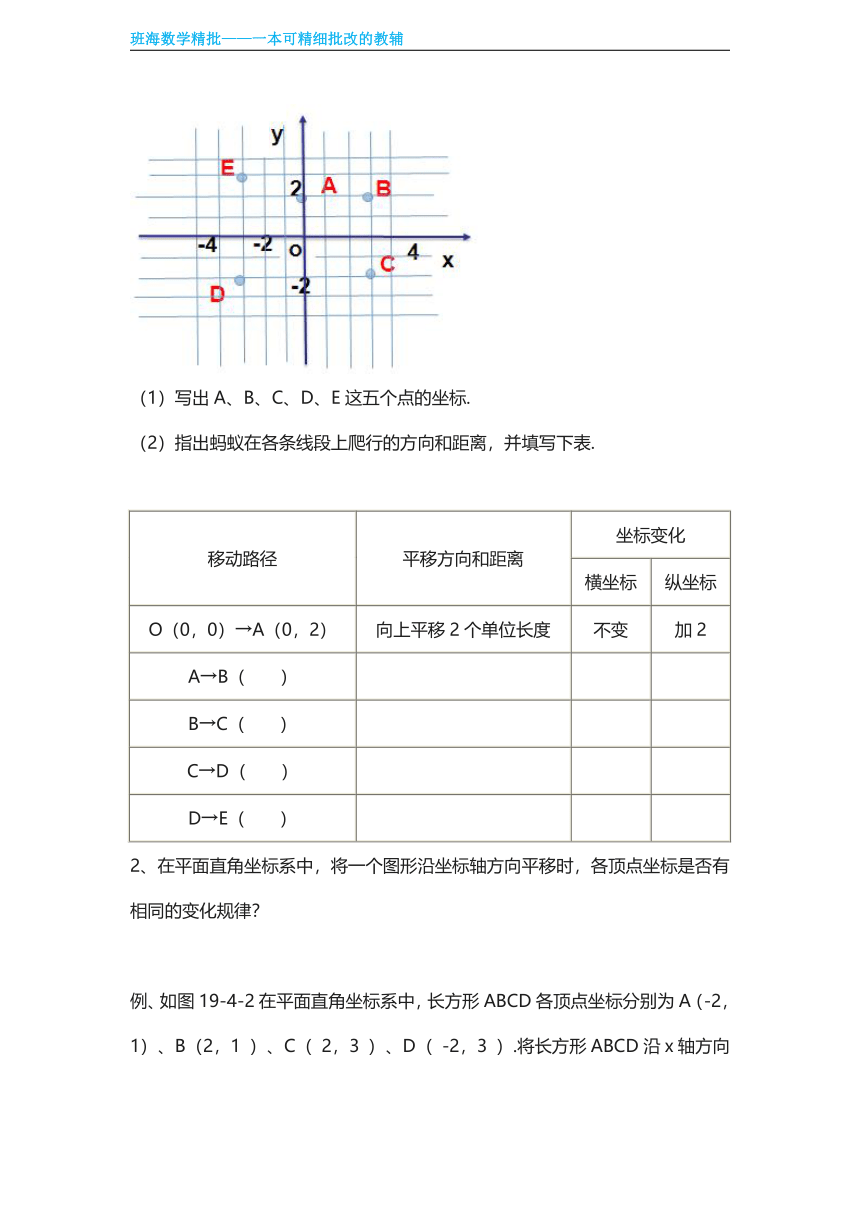
在平面直角坐标系中,一只蚂蚁从原点出发,爬行路径如图19-4-1所示,
(1)写出A、B、C、D、E这五个点的坐标.
(2)指出蚂蚁在各条线段上爬行的方向和距离,并填写下表.
移动路径 平移方向和距离 坐标变化
横坐标 纵坐标
O(0,0)→A(0,2) 向上平移2个单位长度 不变 加2
A→B( )
B→C( )
C→D( )
D→E( )
2、在平面直角坐标系中,将一个图形沿坐标轴方向平移时,各顶点坐标是否有相同的变化规律?
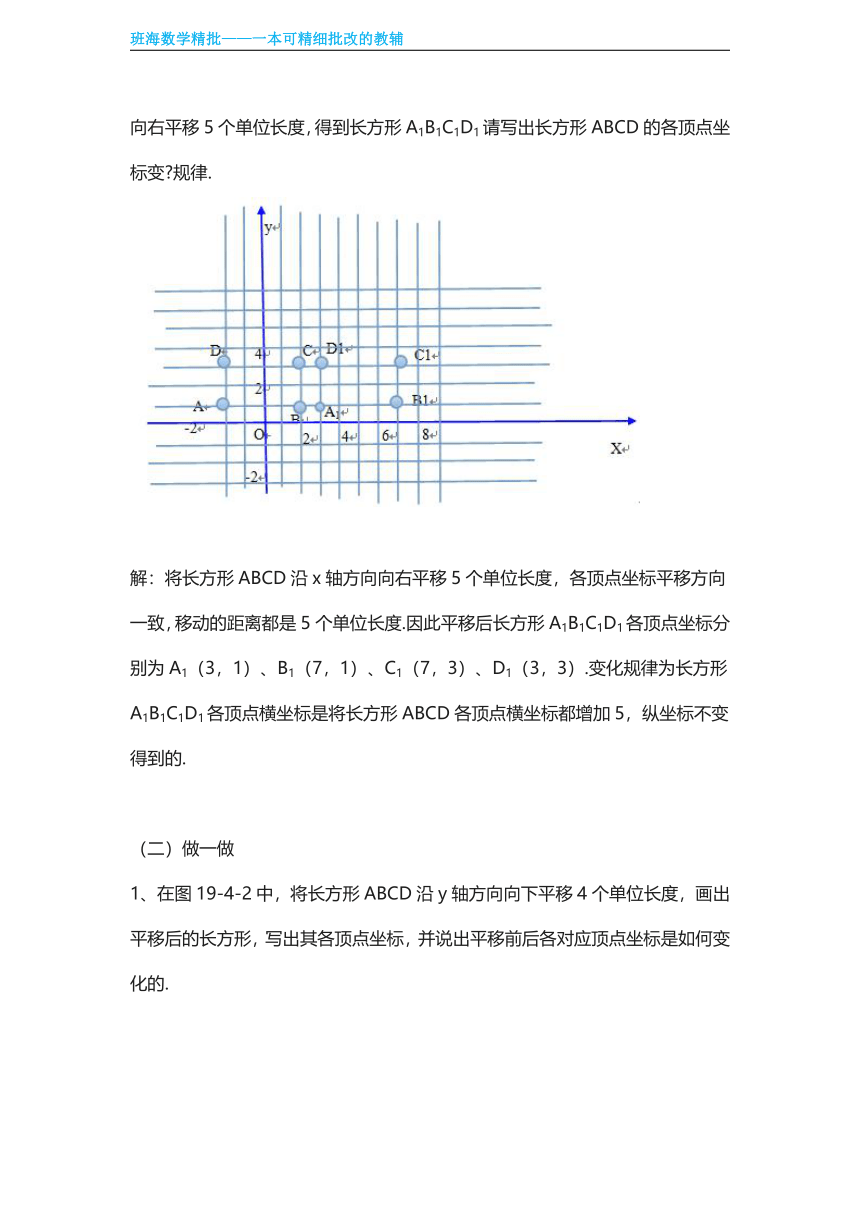
例、如图19-4-2在平面直角坐标系中,长方形ABCD各顶点坐标分别为A(-2,1)、B(2,1 )、C( 2,3 )、D( -2,3 ).将长方形ABCD沿x轴方向向右平移5个单位长度,得到长方形A1B1C1D1请写出长方形ABCD的各顶点坐标变 规律.
解:将长方形ABCD沿x轴方向向右平移5个单位长度,各顶点坐标平移方向一致,移动的距离都是5个单位长度.因此平移后长方形A1B1C1D1各顶点坐标分别为A1(3,1)、B1(7,1)、C1(7,3)、D1(3,3).变化规律为长方形A1B1C1D1各顶点横坐标是将长方形ABCD各顶点横坐标都增加5,纵坐标不变得到的.
(二)做一做
1、在图19-4-2中,将长方形ABCD沿y轴方向向下平移4个单位长度,画出平移后的长方形,写出其各顶点坐标,并说出平移前后各对应顶点坐标是如何变化的.
2、在图19-4-2中,将长方形ABCD沿x轴方向向右平移6个单位长度,再沿y轴方向向右平移5个单位长度.画出平移后的长方形,写出其各顶点坐标,并说出平移前后各对应顶点坐标是如何变化的.
总结规律:在平面直角坐标系中,对于坐标平面上任意一点P(x,y)将它沿x轴方向向右(或向左)平移k个单位长度,相当于将这点的横坐标都增加(或减少)k,纵坐标不变,即点将P(x,y)移动到P·(x+k,y)(或P·(x-k,y));将它沿y轴方向向上(或向下)平移k个单位长度,相当于将这点的横坐标不变,纵坐标都增加(或减少)k,即点将P(x,y)移动到P·(x,y+k)(或P·(x,y-k)).
(三)练习
1、已知平面直角坐标系中一点P(1,1)写出这个点向下平移2个单位长度,再向左平移2个单位长度后的坐标.
2、平面直角坐标系中已知线段AB的端点A(-3,3)、B(-5,0),点P(x,y)是线段AB上任意一点,根据线段平移情况写出平移后A、B、P对应的坐标.
平移方向和距离 A(-3,3) B(-5,0) P(x,y)
向左平移4个单位长度
向下平移3个单位长度
向右平移2个单位长度,向上平移4个单位长度
向左平移3个单位长度,向下平移5个单位长度
(四)小结
引导学生总结本节的主要知识点.
(五)板书设计
19.4.1 用坐标表示平移一起探究做一做练习
用坐标表示图形的对称、放大和缩小
(一)一起探究1
△ABC各顶点的坐标分别为A(-5,1),B(-1,1),C(-2,4),请你在平面直角坐标系中描出各点并画出△ABC。
①分别把点A、B、C关于x轴和y轴的对称点的坐标填写在下表中
△ABC顶点坐标 A(-5,1) B(-1,1) C(-2,4)
关于x轴的对称点
关于y轴的对称点
②在上图中作出与△ABC关于x轴对称的 ,关于y轴对称的
③根据对应顶点坐标的变化规律,描述关于x轴,y轴对称的两个三角形对应顶点坐标之间的关系。
注:可以先让学生小组交流,练习叙述,最后在班内统一。
实际上,我们有下列结果:
关于x轴对称的两个图形,各对应点的横坐标相等,纵坐标互为相反数;关于y轴对称的两个图形,各对应点的横坐标互为相反数,纵坐标相等。
(二)一起探究2
1、五边形OABCD各顶点的坐标分别为O(0,0),A(0,2),B(2,3),C(4,2),D(3,0),请你在平面直角坐标系中描出各点并画出五边形OABCD。
①将各顶点的横坐标和纵坐标都乘以2,写出各对应点的坐标。
②在直角坐标系中,描出这些点并依次连接得到五边形 与五边形OABCD相比较,形状和大小有什么变化?
2、四边形OABC各顶点的坐标分别为O(0,0),A(2,6),B(6,6),C(8,0),请你在平面直角坐标系中描出各点并画出四边形OABC。
①将各顶点的横坐标和纵坐标都乘以 ,写出各对应点的坐标。
②在直角坐标系中,描出这些点并依次连接得到四边形 与四边形OABC相比较,形状和大小有什么变化?
3、分别过每对对应点画直线,你能发现什么结果?
结论:将一个图形各顶点的横纵坐标都乘以k(或),所得图形的形状不变,各边扩大到原来的k倍(或缩小为原来的 ),且连接各对应顶点的直线相交于一点。
(三)练习
(四)小结
引导学生总结本节的主要知识点。
在直角坐标系中,设点P的坐标是(x0,y0).
①如果点P1与点P关于x轴对称,那么点P的坐标是(x0,-y0).
②如果点P2与点P关于y轴对称,那么点P2的坐标是(-x0,y0).
③如果点Q的坐标是(mx0,y0)(m>0),那么点Q到y轴的距离等于点P到y轴距离的m倍,且点Q与点P在与x轴平行的同一条直线上.
④如果点P的坐标是(x0,ny0)(n>0),那么点R到x轴的距离等于点P到x轴距离的n倍,且点R与点P在与y轴平行的同一条直线上.
(五)板书设计
坐标与图形的变化(2)一起探究1 结论一起探究2练习
作业:P50 A组、B组题。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
19.4 坐标与图形的变化
用坐标表示平移
一、教学目标
初步掌握点的坐标变化与点的平移关系,进而理解图形各个点的坐标变化与图形平移的关系,并解决与平移有关的问题.
经历探索点的平移与点的坐标变化之间的规律过程,体会数形结合思想. 了解利用图形的平移变换解决简单问题.
培养学生主动探索的精神,提高学生的学习兴趣.
二、教学重点和难点
教学重点是让学生发现并归纳点的坐标变化与点的平移的关系;教学难点是文字语言、图形语言、坐标表示之间的转化以及应用.
三、教学方法和教学手段
本课采用教师的启发引导与学生的自主探究相结合的教学方法,利用多媒体等手段教学.
四、教学过程设计与实施
根据班级学生基础较好的特点,我把这节课分为五个环节:
(一)一起探究
在平面直角坐标系中,一只蚂蚁从原点出发,爬行路径如图19-4-1所示,
(1)写出A、B、C、D、E这五个点的坐标.
(2)指出蚂蚁在各条线段上爬行的方向和距离,并填写下表.
移动路径 平移方向和距离 坐标变化
横坐标 纵坐标
O(0,0)→A(0,2) 向上平移2个单位长度 不变 加2
A→B( )
B→C( )
C→D( )
D→E( )
2、在平面直角坐标系中,将一个图形沿坐标轴方向平移时,各顶点坐标是否有相同的变化规律?
例、如图19-4-2在平面直角坐标系中,长方形ABCD各顶点坐标分别为A(-2,1)、B(2,1 )、C( 2,3 )、D( -2,3 ).将长方形ABCD沿x轴方向向右平移5个单位长度,得到长方形A1B1C1D1请写出长方形ABCD的各顶点坐标变 规律.
解:将长方形ABCD沿x轴方向向右平移5个单位长度,各顶点坐标平移方向一致,移动的距离都是5个单位长度.因此平移后长方形A1B1C1D1各顶点坐标分别为A1(3,1)、B1(7,1)、C1(7,3)、D1(3,3).变化规律为长方形A1B1C1D1各顶点横坐标是将长方形ABCD各顶点横坐标都增加5,纵坐标不变得到的.
(二)做一做
1、在图19-4-2中,将长方形ABCD沿y轴方向向下平移4个单位长度,画出平移后的长方形,写出其各顶点坐标,并说出平移前后各对应顶点坐标是如何变化的.
2、在图19-4-2中,将长方形ABCD沿x轴方向向右平移6个单位长度,再沿y轴方向向右平移5个单位长度.画出平移后的长方形,写出其各顶点坐标,并说出平移前后各对应顶点坐标是如何变化的.
总结规律:在平面直角坐标系中,对于坐标平面上任意一点P(x,y)将它沿x轴方向向右(或向左)平移k个单位长度,相当于将这点的横坐标都增加(或减少)k,纵坐标不变,即点将P(x,y)移动到P·(x+k,y)(或P·(x-k,y));将它沿y轴方向向上(或向下)平移k个单位长度,相当于将这点的横坐标不变,纵坐标都增加(或减少)k,即点将P(x,y)移动到P·(x,y+k)(或P·(x,y-k)).
(三)练习
1、已知平面直角坐标系中一点P(1,1)写出这个点向下平移2个单位长度,再向左平移2个单位长度后的坐标.
2、平面直角坐标系中已知线段AB的端点A(-3,3)、B(-5,0),点P(x,y)是线段AB上任意一点,根据线段平移情况写出平移后A、B、P对应的坐标.
平移方向和距离 A(-3,3) B(-5,0) P(x,y)
向左平移4个单位长度
向下平移3个单位长度
向右平移2个单位长度,向上平移4个单位长度
向左平移3个单位长度,向下平移5个单位长度
(四)小结
引导学生总结本节的主要知识点.
(五)板书设计
19.4.1 用坐标表示平移一起探究做一做练习
用坐标表示图形的对称、放大和缩小
(一)一起探究1
△ABC各顶点的坐标分别为A(-5,1),B(-1,1),C(-2,4),请你在平面直角坐标系中描出各点并画出△ABC。
①分别把点A、B、C关于x轴和y轴的对称点的坐标填写在下表中
△ABC顶点坐标 A(-5,1) B(-1,1) C(-2,4)
关于x轴的对称点
关于y轴的对称点
②在上图中作出与△ABC关于x轴对称的 ,关于y轴对称的
③根据对应顶点坐标的变化规律,描述关于x轴,y轴对称的两个三角形对应顶点坐标之间的关系。
注:可以先让学生小组交流,练习叙述,最后在班内统一。
实际上,我们有下列结果:
关于x轴对称的两个图形,各对应点的横坐标相等,纵坐标互为相反数;关于y轴对称的两个图形,各对应点的横坐标互为相反数,纵坐标相等。
(二)一起探究2
1、五边形OABCD各顶点的坐标分别为O(0,0),A(0,2),B(2,3),C(4,2),D(3,0),请你在平面直角坐标系中描出各点并画出五边形OABCD。
①将各顶点的横坐标和纵坐标都乘以2,写出各对应点的坐标。
②在直角坐标系中,描出这些点并依次连接得到五边形 与五边形OABCD相比较,形状和大小有什么变化?
2、四边形OABC各顶点的坐标分别为O(0,0),A(2,6),B(6,6),C(8,0),请你在平面直角坐标系中描出各点并画出四边形OABC。
①将各顶点的横坐标和纵坐标都乘以 ,写出各对应点的坐标。
②在直角坐标系中,描出这些点并依次连接得到四边形 与四边形OABC相比较,形状和大小有什么变化?
3、分别过每对对应点画直线,你能发现什么结果?
结论:将一个图形各顶点的横纵坐标都乘以k(或),所得图形的形状不变,各边扩大到原来的k倍(或缩小为原来的 ),且连接各对应顶点的直线相交于一点。
(三)练习
(四)小结
引导学生总结本节的主要知识点。
在直角坐标系中,设点P的坐标是(x0,y0).
①如果点P1与点P关于x轴对称,那么点P的坐标是(x0,-y0).
②如果点P2与点P关于y轴对称,那么点P2的坐标是(-x0,y0).
③如果点Q的坐标是(mx0,y0)(m>0),那么点Q到y轴的距离等于点P到y轴距离的m倍,且点Q与点P在与x轴平行的同一条直线上.
④如果点P的坐标是(x0,ny0)(n>0),那么点R到x轴的距离等于点P到x轴距离的n倍,且点R与点P在与y轴平行的同一条直线上.
(五)板书设计
坐标与图形的变化(2)一起探究1 结论一起探究2练习
作业:P50 A组、B组题。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
