5.1.2垂线 教学课件 (共38张PPT)
文档属性
| 名称 | 5.1.2垂线 教学课件 (共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 16:49:20 | ||
图片预览







文档简介
(共38张PPT)
第五章 相交线与平行线
5.1 相交线
5.1.2 垂线
新课导入
讲授新课
当堂检测
课堂小结
情景引入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
集思广益:日常生活里,图中的两条直线的关系很常见,你还能举出其他例子吗?
知识点一 垂线的定义理解
知识精讲
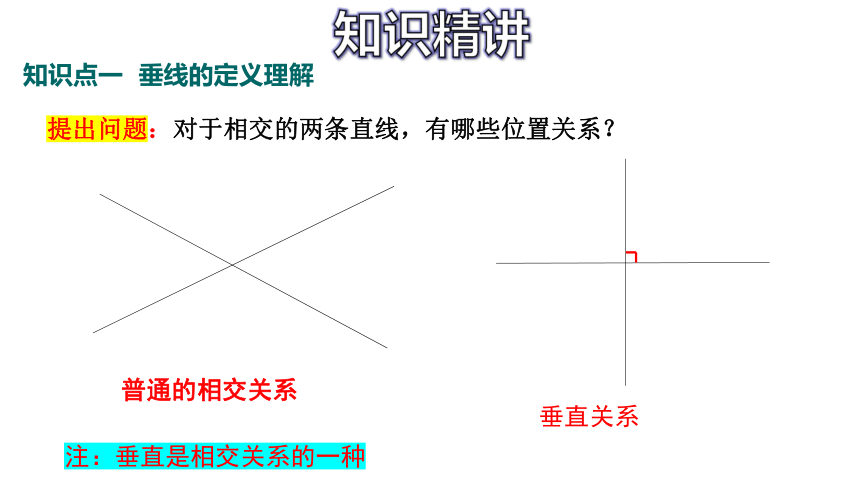
提出问题:对于相交的两条直线,有哪些位置关系?
普通的相交关系
垂直关系
注:垂直是相交关系的一种
知识精讲
思考问题:如图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC的度数是多少?为什么?
A
B
C
D
O
∵∠AOC=90°
∴∠BOC+∠AOC=180°
∴∠BOC=90°
同理可得:∠AOD=∠BOD=90°
根据邻补角的性质即可得到结论;
知识精讲
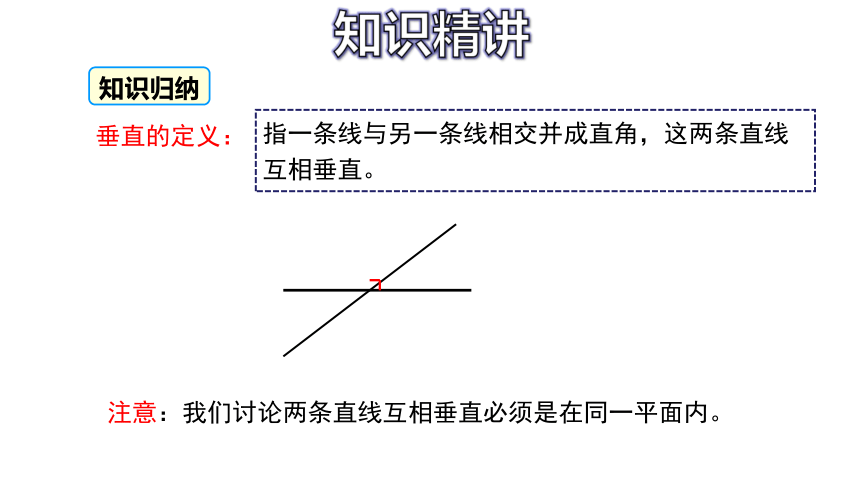
指一条线与另一条线相交并成直角,这两条直线互相垂直。
注意:我们讨论两条直线互相垂直必须是在同一平面内。
垂直的定义:
知识归纳
知识精讲
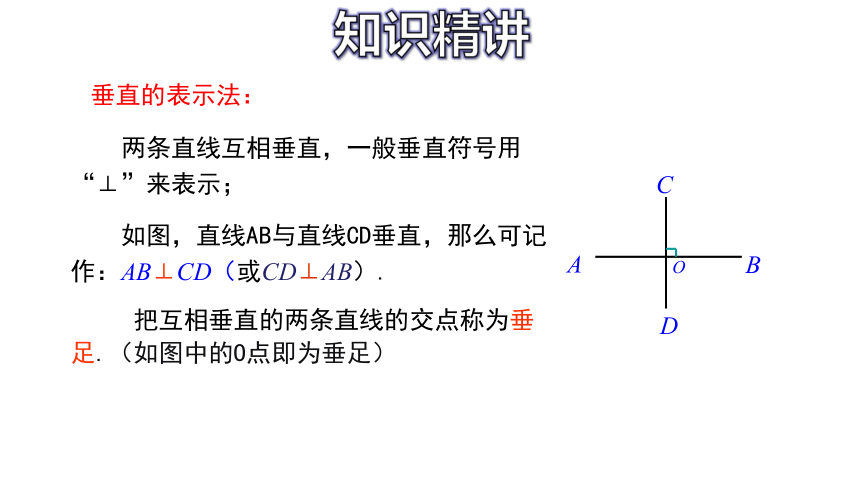
两条直线互相垂直,一般垂直符号用“⊥”来表示;
如图,直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
把互相垂直的两条直线的交点称为垂足.(如图中的O点即为垂足)
A
B
C
D
O
垂直的表示法:
知识精讲
①判定:两条直线相交成90°
②性质:两条直线互相垂直所形成的四个角均为90°
垂线的基本性质与判定
典型例题
典例精析
【例1】如图,直线AB,CD相交于点0,下列条件:①∠AOD=90°;②∠AOC=∠BOC;③∠AOC=∠BOD,其中能说明AB⊥CD的有( )
A.① B.①或② C.①或③ D.①或②或③
【答案】B
【分析】根据垂直定义“当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直”进行判定即可.
练一练
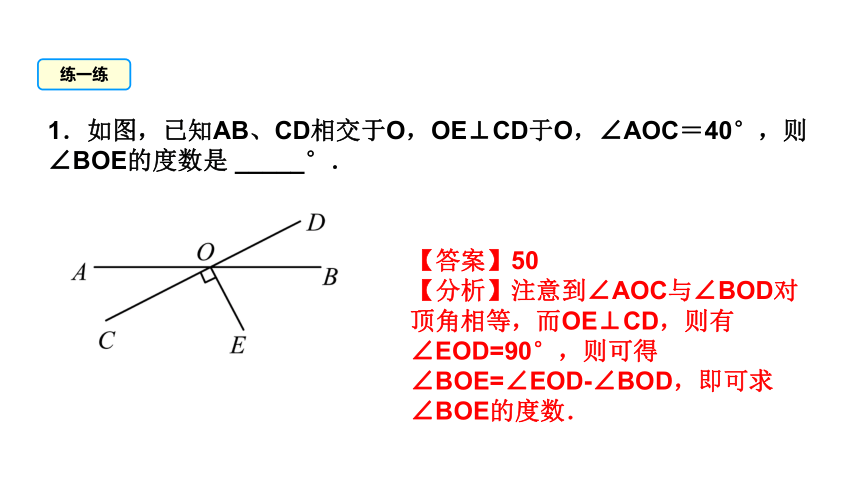
1.如图,已知AB、CD相交于O,OE⊥CD于O,∠AOC=40°,则∠BOE的度数是 _____°.
【答案】50
【分析】注意到∠AOC与∠BOD对顶角相等,而OE⊥CD,则有∠EOD=90°,则可得∠BOE=∠EOD-∠BOD,即可求∠BOE的度数.
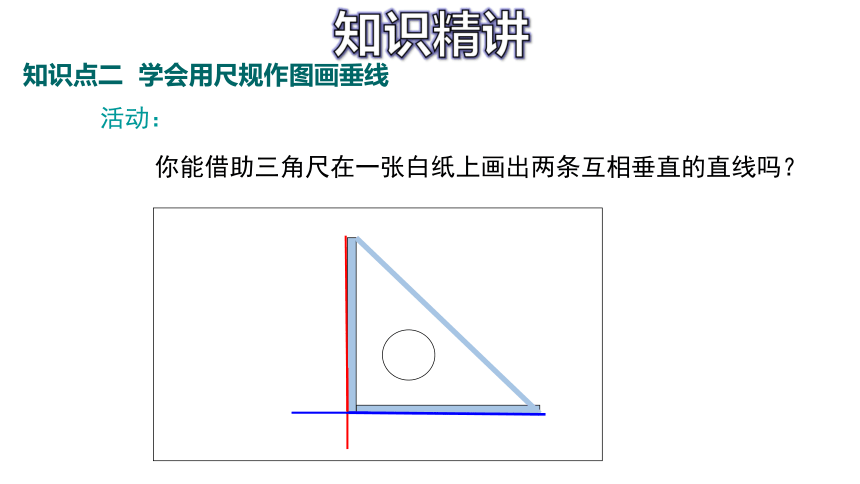
知识点二 学会用尺规作图画垂线
知识精讲
你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
活动:
知识精讲
问题:
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条
A
.B
l
.
知识精讲
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论
问题:这样画l的垂线可以画几条?
一条
知识精讲
垂线的性质:过直线上或直线外的一点,有且只有一条直线和已知直线垂直。
注意:
1.过一点既可以是在直线上,也可以是在直线外的一点;
2.有且只有是指这样的直线只有一条;
概念归纳
典型例题
典例精析
【例2】过点A画线段BC所在直线的垂线段,其中正确的是( )
A. B.
C. D.
【答案】D
【分析】根据垂线段的定义依次判断每个选项.
练一练
1.如图,一束光线以入射角为50°的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成30°的角,则CD与地面AB所成的角∠CDA的度数是_____.
【详解】解:过点E作EM⊥CD于E.
根据题意得:∠1=∠2=50°,∠END=30°,
∴∠DEN=40°,
∴∠CDA=∠DEN+∠END=30°+40°=70°.
故答案为70°.
知识点三 点到直线的距离
知识精讲
C
D
E
l
B
A
过河问题
如图,小明要从A点过河,目测有B、C、D、E四个地点,哪个地点的距离是最短的?
知识精讲
连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
概念归纳
D
l
A
典型例题
典例精析
【例3】如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,则图中能表示点到直线距离的垂线段共有( )
A.2条 B.3条 C.4条 D.5条
【答案】D
【分析】根据点到直线的距离的定义,得结论.
【详解】解:点C到AB的距离是线段CD的长度,
点B到CD的距离是线段BD的长度,
点A到CD的距离是线段AD的长度,
点A到CB的距离是线段CA的长度,
点B到AC的距离是线段BC的长度,
综上,图中能表示点到直线距离的垂线段共有5条,
故选:D.
练一练
1.如图,BC⊥AC,BC=8cm,AC=6cm,AB=10cm.那么点B到AC的距离是 _____,点A、B两点的距离是 _____,点C到AB的距离是 _____.
【答案】 8cm 10cm 4.8cm
【分析】过点C作CD⊥AB于点D,则线段CD的长即为点C到AB的距离,再根据三角形的面积公式求出CD的长;再根据点到直线距离的定义即可得出结论.
2.如图,AB交CD于O,OE⊥AB.若∠AOC:∠BOC=1:2,求∠EOD的度数.
【答案】∠DOE=30°
【点睛】本题考查的是邻补角的含义,垂直的定义,掌握“利用邻补角的含义求解角的大小”是解本题的关键.
【详解】解:∵∠AOC:∠BOC=1:2,
∠AOB=180°,
∴∠AOC=,
∵OE⊥AB,
∴∠AOE=90°,
∴∠DOE=180°-90°-60°=30°.
3.如图,直线AB与CD相交于O,OF,OD分别是∠AOE,∠BOE的平分线;
(1)若∠BOE=62°,求∠AOD和∠EOF的度数;
(2)试问射线OD与OF之间有什么特殊的位置关系?为什么?
【答案】(1)∠AOD=149°,∠EOF=59°
(2)OD⊥OF,
(1)解:∵OD是∠BOE的平分线,∴∠BOD=∠DOE=,
∴∠AOD=180°-∠BOD=180°-31°=149°,
又∵OF是∠AOE的平分线,∴∠EOF=∠AOF=∠AOE=59°
(2)解:OD⊥OF,理由如下:
∵OD是∠BOE的平分线,∴∠BOD=∠DOE=,
又∵OF是∠AOE的平分线,∴∠EOF=∠AOF=∠AOE,
∴∠DOE+∠EOF=×180°=90°
即OD⊥OF.
课堂练习
1.下列说法正确的是( )
A.相等的两个角是对顶角
B.两条直线相交所形成的四个角都相等,则这两条直线互相垂直
C.若两直线相交,则它们互相垂直
D.和等于180度的两个角互为邻补角
【答案】B
【详解】A、如图1,
∠AOC=∠BOC=90°,但∠AOC与∠BOC不是对顶角,故A选项错误;
B、两条直线相交所形成的四个角都相等,则每个角都是90°,符合两条直线互相垂直的定义,故B选项正确
C、两线相交但不一定垂直,故C选项错误.
D、如图2,
∠1+∠2=180°,但∠1与∠2并非互为邻补角,故D选项错误.
故选:B.
2.如图,是测量学生跳远成绩的示意图,即PA的长为某同学的跳远成绩,其依据是( )
A.两点之间线段最短 B.两点确定一条直线
C.垂线段最短 D.过一点有且只有一条直线与已知直线垂直
【答案】C
【分析】由点到直线的距离的定义及跳远比赛的规则作出判断.
【详解】解:能正确解释这一现象的数学知识是垂线段最短,
故选:C.
3.如图,直AB线CD,相交于点E,EF⊥AB于点E,若∠FEC-∠AEC=20°,那么∠AFD的度数为( )
A.125° B.135° C.140° D.145°
【答案】D
【点睛】本题考查了垂直角及互补角的性质,理解题意是解题的关键.
【详解】设∠AEC为x,则∠FEC=x+20°,
∵EF⊥AB,
∴∠AEF=90°,
∴∠AEC+∠FEC=90°,
∴x+x+20°=90°,
解得x=35°,
即∠AEC=35°,
∴∠AED=180°-35°=145°.
4.如图,直线AB,CD相交于点O,OE⊥AB.OF平分∠EOD,∠AOC=46°,则∠FOB的度数为( )
A.68° B.58° C.73° D.63°
【详解】解:∵OE⊥AB
∴∠BOE=90°,
∵∠BOD=∠AOC=46°,
∴∠DOE=∠BOE-∠BOD=90°-46°=44°,
∵OF平分∠EOD,
∴∠EOF=∠DOE=22°,
∴∠FOB=∠BOE-∠EOF=90°-22°=68°,
故选:A.
5.如图,OA⊥OB,OC⊥OD,O是垂足,∠AOD=120°,那么∠COB的度数为______;
【详解】解:∵OA⊥OB,OC⊥OD,
∴∠AOB=90°
∵∠AOD=120°
∴∠BOD=120°-90°=30°
∠BOC=60°
故答案为:60°.
6.直线AB,CD相交于点O,OE平分∠BOD,OF⊥CD,作射线OG⊥OE.若∠EOF=54°,则∠AOG的度数为______.
【详解】解:∵OF⊥CD,
∴∠FOD=90°,
∵∠EOF=54°,
∴∠DOE=∠FOD-∠EOF=90°-54°=36°,
∵∴OE平分∠BOD,
∴∠BOD=2∠DOE=72°,
分两种情况:
当射线OG在OE的下方,如图:
∵OG⊥OE,
∴∠EOG=90°,
∵OE平分∠BOD,
∴∠BOE=∠BOD=36°,
∴∠AOG=180°-∠EOG-∠BOE=54°;
当射线OG在OE的上方,如图:
∵OG⊥OE,∴∠EOG=90°,
∵∠DOE=36°,
∴∠COG=180°-∠EOG-∠DOE=54°,
∴∠AOG=∠AOC+∠COG=∠BOD+∠COG=72°+54°=126°,
综上所述:∠AOG的度数为:54°或126°,
故答案为:54°或126°.
7.已知A,B,C三地位置如图所示,∠C=90°,AC=4,BC=3,则A到BC距离是______.若A地在C地的正东方向,则B地在C地的______方向.
【答案】 4 正北
【分析】直接根据点到直线的距离的概念即可得出答案;
【详解】解:∵∠C=90°,AC=4,
∴A到BC距离是AC=4
∵ A地在C地的正东方向,
∴B地在C地的正北方向
故答案为:4,正北.
8.如图,点A、点B是直线l上两点,AB=10,点M在直线l外,MB=6,MA=8,∠AMB=90°,若点P为直线l上一动点,连接MP,则线段MP的最小值是____.
【答案】4.8
【分析】根据垂线段最短可知:当MP⊥AB时,MP有最小值,利用三角形的面积可列式计算求解MP的最小值.
9.如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
【答案】(1)145°
(2)125°
【点睛】本题考查的是邻补角的性质、对顶角的性质和角平分线的定义,垂直的定义,几何图形中角度的计算,掌握邻补角互补、对顶角相等和垂直的定义是解题的关键.
(1)
解:∵∠AOC:∠AOD=7:11,∠AOC+∠AOD=180°
∴∠AOC=,
∴∠DOB=∠AOC=70°,
又∵OE平分∠BOD,
∴∠DOE=,
∴∠COE=180°-∠DOE=180°-35°=145°,
(2)
∵OF⊥OE,
∴∠EOF=90°,
∴∠FOD=90°-∠DOE=90°-35°=55°,
∴∠COF=180°-∠FOD=180°-55°=125°.
课堂总结
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂线的定义
2.垂线的画法
3.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直,
(2)垂线段最短.
4.点到直线的距离
第五章 相交线与平行线
5.1 相交线
5.1.2 垂线
新课导入
讲授新课
当堂检测
课堂小结
情景引入
观察下面图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
集思广益:日常生活里,图中的两条直线的关系很常见,你还能举出其他例子吗?
知识点一 垂线的定义理解
知识精讲
提出问题:对于相交的两条直线,有哪些位置关系?
普通的相交关系
垂直关系
注:垂直是相交关系的一种
知识精讲
思考问题:如图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC的度数是多少?为什么?
A
B
C
D
O
∵∠AOC=90°
∴∠BOC+∠AOC=180°
∴∠BOC=90°
同理可得:∠AOD=∠BOD=90°
根据邻补角的性质即可得到结论;
知识精讲
指一条线与另一条线相交并成直角,这两条直线互相垂直。
注意:我们讨论两条直线互相垂直必须是在同一平面内。
垂直的定义:
知识归纳
知识精讲
两条直线互相垂直,一般垂直符号用“⊥”来表示;
如图,直线AB与直线CD垂直,那么可记作:AB⊥CD(或CD⊥AB).
把互相垂直的两条直线的交点称为垂足.(如图中的O点即为垂足)
A
B
C
D
O
垂直的表示法:
知识精讲
①判定:两条直线相交成90°
②性质:两条直线互相垂直所形成的四个角均为90°
垂线的基本性质与判定
典型例题
典例精析
【例1】如图,直线AB,CD相交于点0,下列条件:①∠AOD=90°;②∠AOC=∠BOC;③∠AOC=∠BOD,其中能说明AB⊥CD的有( )
A.① B.①或② C.①或③ D.①或②或③
【答案】B
【分析】根据垂直定义“当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直”进行判定即可.
练一练
1.如图,已知AB、CD相交于O,OE⊥CD于O,∠AOC=40°,则∠BOE的度数是 _____°.
【答案】50
【分析】注意到∠AOC与∠BOD对顶角相等,而OE⊥CD,则有∠EOD=90°,则可得∠BOE=∠EOD-∠BOD,即可求∠BOE的度数.
知识点二 学会用尺规作图画垂线
知识精讲
你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
活动:
知识精讲
问题:
(1)画已知直线l的垂线能画几条
(2)过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)过直线l外的一点B画l的垂线,这样的垂线能画几条
A
.B
l
.
知识精讲
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论
问题:这样画l的垂线可以画几条?
一条
知识精讲
垂线的性质:过直线上或直线外的一点,有且只有一条直线和已知直线垂直。
注意:
1.过一点既可以是在直线上,也可以是在直线外的一点;
2.有且只有是指这样的直线只有一条;
概念归纳
典型例题
典例精析
【例2】过点A画线段BC所在直线的垂线段,其中正确的是( )
A. B.
C. D.
【答案】D
【分析】根据垂线段的定义依次判断每个选项.
练一练
1.如图,一束光线以入射角为50°的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成30°的角,则CD与地面AB所成的角∠CDA的度数是_____.
【详解】解:过点E作EM⊥CD于E.
根据题意得:∠1=∠2=50°,∠END=30°,
∴∠DEN=40°,
∴∠CDA=∠DEN+∠END=30°+40°=70°.
故答案为70°.
知识点三 点到直线的距离
知识精讲
C
D
E
l
B
A
过河问题
如图,小明要从A点过河,目测有B、C、D、E四个地点,哪个地点的距离是最短的?
知识精讲
连接直线外一点与直线上各点的所有线段中,垂线段最短.简单说成:垂线段最短.
概念归纳
D
l
A
典型例题
典例精析
【例3】如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,则图中能表示点到直线距离的垂线段共有( )
A.2条 B.3条 C.4条 D.5条
【答案】D
【分析】根据点到直线的距离的定义,得结论.
【详解】解:点C到AB的距离是线段CD的长度,
点B到CD的距离是线段BD的长度,
点A到CD的距离是线段AD的长度,
点A到CB的距离是线段CA的长度,
点B到AC的距离是线段BC的长度,
综上,图中能表示点到直线距离的垂线段共有5条,
故选:D.
练一练
1.如图,BC⊥AC,BC=8cm,AC=6cm,AB=10cm.那么点B到AC的距离是 _____,点A、B两点的距离是 _____,点C到AB的距离是 _____.
【答案】 8cm 10cm 4.8cm
【分析】过点C作CD⊥AB于点D,则线段CD的长即为点C到AB的距离,再根据三角形的面积公式求出CD的长;再根据点到直线距离的定义即可得出结论.
2.如图,AB交CD于O,OE⊥AB.若∠AOC:∠BOC=1:2,求∠EOD的度数.
【答案】∠DOE=30°
【点睛】本题考查的是邻补角的含义,垂直的定义,掌握“利用邻补角的含义求解角的大小”是解本题的关键.
【详解】解:∵∠AOC:∠BOC=1:2,
∠AOB=180°,
∴∠AOC=,
∵OE⊥AB,
∴∠AOE=90°,
∴∠DOE=180°-90°-60°=30°.
3.如图,直线AB与CD相交于O,OF,OD分别是∠AOE,∠BOE的平分线;
(1)若∠BOE=62°,求∠AOD和∠EOF的度数;
(2)试问射线OD与OF之间有什么特殊的位置关系?为什么?
【答案】(1)∠AOD=149°,∠EOF=59°
(2)OD⊥OF,
(1)解:∵OD是∠BOE的平分线,∴∠BOD=∠DOE=,
∴∠AOD=180°-∠BOD=180°-31°=149°,
又∵OF是∠AOE的平分线,∴∠EOF=∠AOF=∠AOE=59°
(2)解:OD⊥OF,理由如下:
∵OD是∠BOE的平分线,∴∠BOD=∠DOE=,
又∵OF是∠AOE的平分线,∴∠EOF=∠AOF=∠AOE,
∴∠DOE+∠EOF=×180°=90°
即OD⊥OF.
课堂练习
1.下列说法正确的是( )
A.相等的两个角是对顶角
B.两条直线相交所形成的四个角都相等,则这两条直线互相垂直
C.若两直线相交,则它们互相垂直
D.和等于180度的两个角互为邻补角
【答案】B
【详解】A、如图1,
∠AOC=∠BOC=90°,但∠AOC与∠BOC不是对顶角,故A选项错误;
B、两条直线相交所形成的四个角都相等,则每个角都是90°,符合两条直线互相垂直的定义,故B选项正确
C、两线相交但不一定垂直,故C选项错误.
D、如图2,
∠1+∠2=180°,但∠1与∠2并非互为邻补角,故D选项错误.
故选:B.
2.如图,是测量学生跳远成绩的示意图,即PA的长为某同学的跳远成绩,其依据是( )
A.两点之间线段最短 B.两点确定一条直线
C.垂线段最短 D.过一点有且只有一条直线与已知直线垂直
【答案】C
【分析】由点到直线的距离的定义及跳远比赛的规则作出判断.
【详解】解:能正确解释这一现象的数学知识是垂线段最短,
故选:C.
3.如图,直AB线CD,相交于点E,EF⊥AB于点E,若∠FEC-∠AEC=20°,那么∠AFD的度数为( )
A.125° B.135° C.140° D.145°
【答案】D
【点睛】本题考查了垂直角及互补角的性质,理解题意是解题的关键.
【详解】设∠AEC为x,则∠FEC=x+20°,
∵EF⊥AB,
∴∠AEF=90°,
∴∠AEC+∠FEC=90°,
∴x+x+20°=90°,
解得x=35°,
即∠AEC=35°,
∴∠AED=180°-35°=145°.
4.如图,直线AB,CD相交于点O,OE⊥AB.OF平分∠EOD,∠AOC=46°,则∠FOB的度数为( )
A.68° B.58° C.73° D.63°
【详解】解:∵OE⊥AB
∴∠BOE=90°,
∵∠BOD=∠AOC=46°,
∴∠DOE=∠BOE-∠BOD=90°-46°=44°,
∵OF平分∠EOD,
∴∠EOF=∠DOE=22°,
∴∠FOB=∠BOE-∠EOF=90°-22°=68°,
故选:A.
5.如图,OA⊥OB,OC⊥OD,O是垂足,∠AOD=120°,那么∠COB的度数为______;
【详解】解:∵OA⊥OB,OC⊥OD,
∴∠AOB=90°
∵∠AOD=120°
∴∠BOD=120°-90°=30°
∠BOC=60°
故答案为:60°.
6.直线AB,CD相交于点O,OE平分∠BOD,OF⊥CD,作射线OG⊥OE.若∠EOF=54°,则∠AOG的度数为______.
【详解】解:∵OF⊥CD,
∴∠FOD=90°,
∵∠EOF=54°,
∴∠DOE=∠FOD-∠EOF=90°-54°=36°,
∵∴OE平分∠BOD,
∴∠BOD=2∠DOE=72°,
分两种情况:
当射线OG在OE的下方,如图:
∵OG⊥OE,
∴∠EOG=90°,
∵OE平分∠BOD,
∴∠BOE=∠BOD=36°,
∴∠AOG=180°-∠EOG-∠BOE=54°;
当射线OG在OE的上方,如图:
∵OG⊥OE,∴∠EOG=90°,
∵∠DOE=36°,
∴∠COG=180°-∠EOG-∠DOE=54°,
∴∠AOG=∠AOC+∠COG=∠BOD+∠COG=72°+54°=126°,
综上所述:∠AOG的度数为:54°或126°,
故答案为:54°或126°.
7.已知A,B,C三地位置如图所示,∠C=90°,AC=4,BC=3,则A到BC距离是______.若A地在C地的正东方向,则B地在C地的______方向.
【答案】 4 正北
【分析】直接根据点到直线的距离的概念即可得出答案;
【详解】解:∵∠C=90°,AC=4,
∴A到BC距离是AC=4
∵ A地在C地的正东方向,
∴B地在C地的正北方向
故答案为:4,正北.
8.如图,点A、点B是直线l上两点,AB=10,点M在直线l外,MB=6,MA=8,∠AMB=90°,若点P为直线l上一动点,连接MP,则线段MP的最小值是____.
【答案】4.8
【分析】根据垂线段最短可知:当MP⊥AB时,MP有最小值,利用三角形的面积可列式计算求解MP的最小值.
9.如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
【答案】(1)145°
(2)125°
【点睛】本题考查的是邻补角的性质、对顶角的性质和角平分线的定义,垂直的定义,几何图形中角度的计算,掌握邻补角互补、对顶角相等和垂直的定义是解题的关键.
(1)
解:∵∠AOC:∠AOD=7:11,∠AOC+∠AOD=180°
∴∠AOC=,
∴∠DOB=∠AOC=70°,
又∵OE平分∠BOD,
∴∠DOE=,
∴∠COE=180°-∠DOE=180°-35°=145°,
(2)
∵OF⊥OE,
∴∠EOF=90°,
∴∠FOD=90°-∠DOE=90°-35°=55°,
∴∠COF=180°-∠FOD=180°-55°=125°.
课堂总结
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂线的定义
2.垂线的画法
3.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直,
(2)垂线段最短.
4.点到直线的距离
