5.1.1相交线 教学课件(共34张PPT)
文档属性
| 名称 | 5.1.1相交线 教学课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 16:58:12 | ||
图片预览









文档简介
(共34张PPT)
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
新课导入
讲授新课
当堂检测
课堂小结
情景引入
观察下列图片,说一说直线与直线的位置关系.
直线与直线相交于一点,并形成了四个角.
你发现了什么?
知识点一 邻补角和对顶角的概念
知识精讲
活动:在使用图中的老虎钳时,当摇动手柄使丝杠旋转,就可以带动活动钳身相对于固定钳身作轴向移动,起夹紧或放松的作用。如果把老虎钳的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题.
知识百科:老虎钳的工作原理是什么?
杠杆原理
知识精讲
思考 老虎钳在使用的过程中,你能说说∠AOC与∠AOD,∠AOC与∠BOD这两对角的位置保持怎样的关系吗?
∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线.
∠AOC和∠AOD有一条公共边AO,且∠AOC的另一边是∠AOD另一边的反向延长线.
A
C
D
B
O
结论:∠AOC+∠AOD=180°
结论:∠AOC=∠BOD
知识精讲
1
2
3
A
B
C
O
邻补角的概念
4
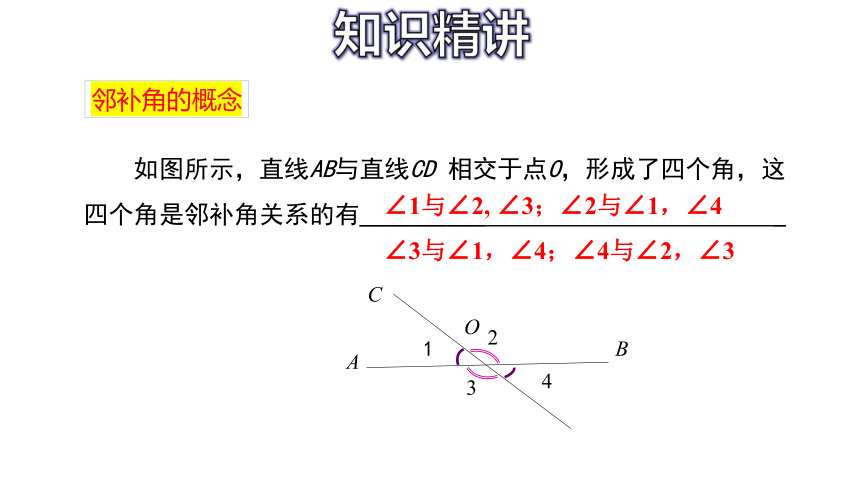
如图所示,直线AB与直线CD 相交于点O,形成了四个角,这四个角是邻补角关系的有__________ _
∠1与∠2, ∠3;∠2与∠1,∠4
∠3与∠1,∠4;∠4与∠2,∠3
知识精讲
两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角;
概念总结
注:
1、必须是两角,单独一个角不构成邻补角关系;
2、两个角须有一条公共边;
3、两个角的另一边是反向延长线的关系;
典型例题
典例精析
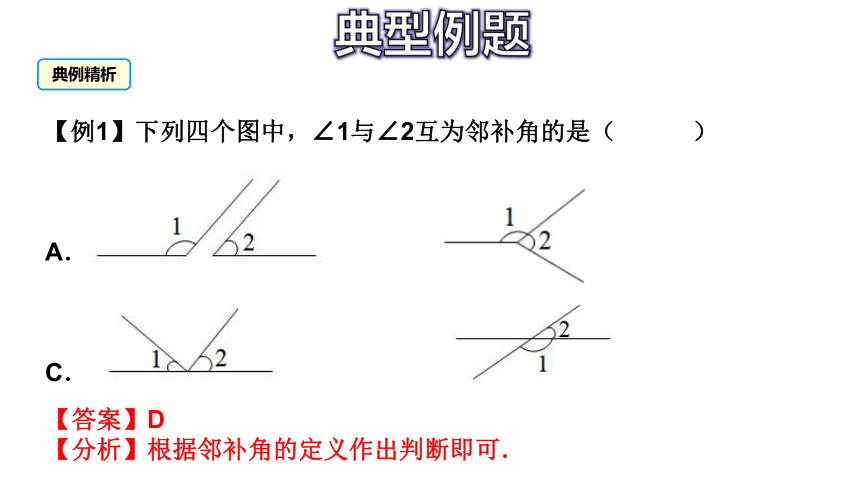
【例1】下列四个图中,∠1与∠2互为邻补角的是( )
A. B.
C. D.
【答案】D
【分析】根据邻补角的定义作出判断即可.
练一练
1.如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
【答案】 反向延长线 ∠2,∠3
知识精讲
1
2
A
B
C
D
O
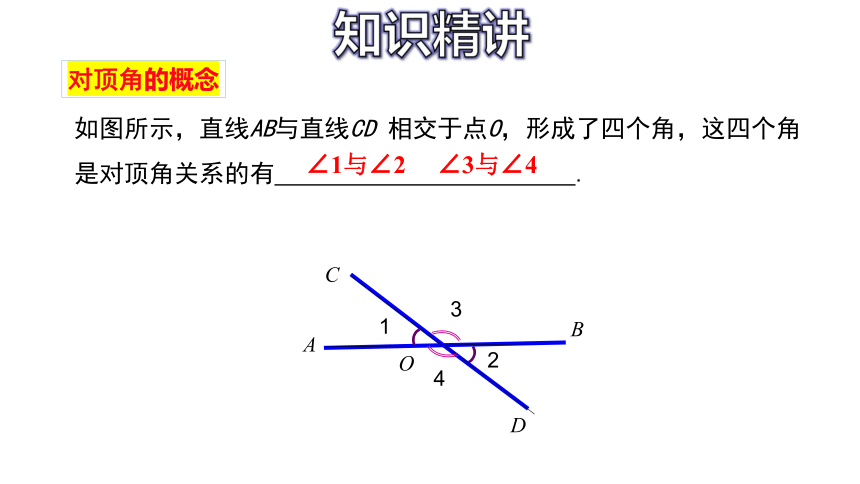
如图所示,直线AB与直线CD 相交于点O,形成了四个角,这四个角是对顶角关系的有 .
∠1与∠2
对顶角的概念
4
3
∠3与∠4
知识精讲
有一个公共端点,并且一个角的两边分别与另一个角的两边互为反向延长线,具有这种位置关系的两个角,互为对顶角。
概念总结
注:
1、必须是两角,单独一个角不构成对顶角关系;
2、两个角须共顶点;
3、两个角的两边均是反向延长线的关系;
典型例题
典例精析
【例2】如图,两条直线AB与CD相交于点O,OE是射线,则图中共有邻补角和对顶角的数量分别为( )
A.6对,2对 B.4对,2对 C.8对,4对 D.4对,4对
【答案】A
【分析】根据邻补角与对顶角的定义找出邻补角和对顶角即可求解.
练一练
1.如图是一把剪刀的示意图,我们可想象成一个相交线模型,若∠AOB+∠COD=72°,则∠AOB=_______.
【答案】36°
知识点二 邻补角和对顶角的性质
知识精讲
∵∠1+∠2=∠AOB=180°(平角的概念)
∴∠1与∠2的和为180°
知识归纳:互为邻补角的两个角的和为180°.
知识探究:观察下列角,说一说∠1与∠2满足什么关系?
C
O
A
B
D
4
3
2
1
知识精讲
问题:我们已经证明出来邻补角的关系,那互为对顶角的∠1 与∠3,∠2与∠4在数量上又有什么关系呢?
头脑风暴:看看谁能想到的证明方法多?
知识精讲
方法一:(测量法)
结论:对顶角相等
O
A
B
C
D
4
3
2
1
先用量角器量出∠1、∠2、∠3、∠4的度数,再进行对比,我们会发现:
∠1=∠3;∠2=∠4
知识精讲
O
A
B
C
D
4
3
2
1
方法二:如图,已知直线AB与CD相交于点O,求证:∠1=∠3, ∠2=∠4.
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°,
∠2+∠3=180°,
∴∠1=∠3(等角的性质).
同理可得∠2=∠4.
性质总结:
对顶角相等;
知识精讲
总结归纳
1、邻补角的性质:一个角与它的邻补角的和等于180°。
2、对顶角的性质:互为对顶角的两个角相等。
典型例题
典例精析
【例3】如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2=( )
A.70° B.60° C.55° D.45°
【答案】A
【详解】解:∵OD平分∠BOC,
∴∠BOC=2∠2.
又∵∠1=40°,∠1+∠BOC=180°,
∴40°+2∠2=180°,
解得∠2=70°.
故选:A.
【例4】如图,直线AB与CD相交于点O,射线OE平分∠BOD,若∠DOE=20°,则∠BOC=_____.
【答案】140°
【分析】根据角平分线的性质求出∠DOB=40,再根据邻补角的定义即可得出∠BOC的度数.
练一练
1.如图,直线AB、CD相交于点O,OE平分∠BOC,∠AOC=40°,则∠BOE的度数为( )
A.50° B.60° C.65° D.70°
【答案】D
【点睛】本题主要考查了邻补角和角平分线的定义,熟练掌握邻补角和角平分线的定义进行求解是解决本题的关键.
2.如图,直线AB、CD相交于点O,若∠AOD=2∠AOC+30°,则∠BOD度数为______.
【详解】解:∵∠AOD=2∠AOC+30°,∠AOD+∠AOC=180°,
∴3∠AOC+30°=180°,
∴∠AOC=50°,
∴∠BOD=∠AOC=50°,
故答案为:50°.
3.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
【答案】(1)∠BOF=33°(2)∠AOC=72°
【分析】(1)先根据对顶角相等求出∠BOD=76°,再由角平分线定义得∠DOE=∠BOE=38°,由邻补角得∠COE=142°,再根据角平分线定义得∠EOF=71°,从而可得结论.
(2)利用角平分的定义得出∠BOE=∠EOD,∠COF=∠FOE,进而表示出各角求出答案.
课堂练习
1.如图所示,∠1和∠2一定相等的是( )
A. B.
C. D.
【答案】D
2.下面四个图形中,∠1与∠2互为邻补角的是( )
A. B. C. D.
【答案】C
【分析】根据邻补角的定义作出判断即可.
3.如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠AOD=130°,则∠EOB度数是( )
A.65° B.50° C.25° D.130°
【答案】A
【点睛】此题主要考查了对顶角相等和角平分线的定义等知识,关键是掌握对顶角相等.
4.如图,AB、CD交于点O,若∠1=70°,射线OE平分∠AOC,那么∠EOD=__________度.
【答案】125
【点睛】本题主要考查了对顶角相等,角平分线的定义,平角的定义,正确求出∠AOD和∠AOE的度数是解题的关键.
5.如图,直线AB与CD相交于点O,∠BOC+∠AOD=288°,那么∠BOC的邻补角是_____度.
【答案】36
【分析】先根据对顶角相等求出∠BOC的度数,再利用邻补角的和等于180°列式计算即可.
6.如图,已知直线AB、CD相交于点O,如果∠AOC=70°,∠BOE:∠EOD=2:3,那么∠EOD的度数是______.
【详解】解:∵∠AOC=∠BOD,∠AOC=70°,
∴∠BOD=70°,
∵∠BOE:∠EOD=2:3,∠BOE+∠EOD=∠BOD,
∴∠EOD=∠BOD=×70°=42°
故答案为:42°.
7.直线AB、CD相交于点O,OE平分∠AOC,射线OF⊥CD于O点,且∠FOE=115°,求∠AOD的度数.
【详解】解:∵OF⊥CD于O点,
∴∠COF=90°
∵∠FOE=115°,
∴∠COE=∠FOE-∠COF=115°-90°=25°,
∵OE平分∠AOC,∠COE=25°,
∴∠AOC=2∠COE=50°,
∴∠AOD=180°-∠AOC=130°.
8.如图,O是直线AB上一点,OD平分∠AOC.
(1)若∠AOC=50°,请求出∠AOD的度数;
(2)若∠AOD和∠DOE互余,且∠AOD=,请求出∠BOC的度数.
(1)
解:∵∠AOC=50°,OD平分∠AOC,
∠AOD=25°
(2)
解:∵∠AOD和∠DOE互余,
∴∠AOE=∠AOD+∠DOE=90°
∴∠AOD=∠AOE=30°,
∵OD平分∠AOC,
∴∠AOC=2∠AOD=60°,
∠BOC=180°-∠AOC=120°
课堂总结
角的 名称 特 征 性 质 相 同 点 不 同 点
对 顶 角
邻 补 角 对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对
①有无公共边;
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
新课导入
讲授新课
当堂检测
课堂小结
情景引入
观察下列图片,说一说直线与直线的位置关系.
直线与直线相交于一点,并形成了四个角.
你发现了什么?
知识点一 邻补角和对顶角的概念
知识精讲
活动:在使用图中的老虎钳时,当摇动手柄使丝杠旋转,就可以带动活动钳身相对于固定钳身作轴向移动,起夹紧或放松的作用。如果把老虎钳的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题.
知识百科:老虎钳的工作原理是什么?
杠杆原理
知识精讲
思考 老虎钳在使用的过程中,你能说说∠AOC与∠AOD,∠AOC与∠BOD这两对角的位置保持怎样的关系吗?
∠AOC和∠BOD有公共顶点,且∠AOC的两边分别是∠BOD两边的反向延长线.
∠AOC和∠AOD有一条公共边AO,且∠AOC的另一边是∠AOD另一边的反向延长线.
A
C
D
B
O
结论:∠AOC+∠AOD=180°
结论:∠AOC=∠BOD
知识精讲
1
2
3
A
B
C
O
邻补角的概念
4
如图所示,直线AB与直线CD 相交于点O,形成了四个角,这四个角是邻补角关系的有__________ _
∠1与∠2, ∠3;∠2与∠1,∠4
∠3与∠1,∠4;∠4与∠2,∠3
知识精讲
两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角;
概念总结
注:
1、必须是两角,单独一个角不构成邻补角关系;
2、两个角须有一条公共边;
3、两个角的另一边是反向延长线的关系;
典型例题
典例精析
【例1】下列四个图中,∠1与∠2互为邻补角的是( )
A. B.
C. D.
【答案】D
【分析】根据邻补角的定义作出判断即可.
练一练
1.如果两个角有一条公共边,它们的另一边互为____________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
【答案】 反向延长线 ∠2,∠3
知识精讲
1
2
A
B
C
D
O
如图所示,直线AB与直线CD 相交于点O,形成了四个角,这四个角是对顶角关系的有 .
∠1与∠2
对顶角的概念
4
3
∠3与∠4
知识精讲
有一个公共端点,并且一个角的两边分别与另一个角的两边互为反向延长线,具有这种位置关系的两个角,互为对顶角。
概念总结
注:
1、必须是两角,单独一个角不构成对顶角关系;
2、两个角须共顶点;
3、两个角的两边均是反向延长线的关系;
典型例题
典例精析
【例2】如图,两条直线AB与CD相交于点O,OE是射线,则图中共有邻补角和对顶角的数量分别为( )
A.6对,2对 B.4对,2对 C.8对,4对 D.4对,4对
【答案】A
【分析】根据邻补角与对顶角的定义找出邻补角和对顶角即可求解.
练一练
1.如图是一把剪刀的示意图,我们可想象成一个相交线模型,若∠AOB+∠COD=72°,则∠AOB=_______.
【答案】36°
知识点二 邻补角和对顶角的性质
知识精讲
∵∠1+∠2=∠AOB=180°(平角的概念)
∴∠1与∠2的和为180°
知识归纳:互为邻补角的两个角的和为180°.
知识探究:观察下列角,说一说∠1与∠2满足什么关系?
C
O
A
B
D
4
3
2
1
知识精讲
问题:我们已经证明出来邻补角的关系,那互为对顶角的∠1 与∠3,∠2与∠4在数量上又有什么关系呢?
头脑风暴:看看谁能想到的证明方法多?
知识精讲
方法一:(测量法)
结论:对顶角相等
O
A
B
C
D
4
3
2
1
先用量角器量出∠1、∠2、∠3、∠4的度数,再进行对比,我们会发现:
∠1=∠3;∠2=∠4
知识精讲
O
A
B
C
D
4
3
2
1
方法二:如图,已知直线AB与CD相交于点O,求证:∠1=∠3, ∠2=∠4.
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°,
∠2+∠3=180°,
∴∠1=∠3(等角的性质).
同理可得∠2=∠4.
性质总结:
对顶角相等;
知识精讲
总结归纳
1、邻补角的性质:一个角与它的邻补角的和等于180°。
2、对顶角的性质:互为对顶角的两个角相等。
典型例题
典例精析
【例3】如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2=( )
A.70° B.60° C.55° D.45°
【答案】A
【详解】解:∵OD平分∠BOC,
∴∠BOC=2∠2.
又∵∠1=40°,∠1+∠BOC=180°,
∴40°+2∠2=180°,
解得∠2=70°.
故选:A.
【例4】如图,直线AB与CD相交于点O,射线OE平分∠BOD,若∠DOE=20°,则∠BOC=_____.
【答案】140°
【分析】根据角平分线的性质求出∠DOB=40,再根据邻补角的定义即可得出∠BOC的度数.
练一练
1.如图,直线AB、CD相交于点O,OE平分∠BOC,∠AOC=40°,则∠BOE的度数为( )
A.50° B.60° C.65° D.70°
【答案】D
【点睛】本题主要考查了邻补角和角平分线的定义,熟练掌握邻补角和角平分线的定义进行求解是解决本题的关键.
2.如图,直线AB、CD相交于点O,若∠AOD=2∠AOC+30°,则∠BOD度数为______.
【详解】解:∵∠AOD=2∠AOC+30°,∠AOD+∠AOC=180°,
∴3∠AOC+30°=180°,
∴∠AOC=50°,
∴∠BOD=∠AOC=50°,
故答案为:50°.
3.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
【答案】(1)∠BOF=33°(2)∠AOC=72°
【分析】(1)先根据对顶角相等求出∠BOD=76°,再由角平分线定义得∠DOE=∠BOE=38°,由邻补角得∠COE=142°,再根据角平分线定义得∠EOF=71°,从而可得结论.
(2)利用角平分的定义得出∠BOE=∠EOD,∠COF=∠FOE,进而表示出各角求出答案.
课堂练习
1.如图所示,∠1和∠2一定相等的是( )
A. B.
C. D.
【答案】D
2.下面四个图形中,∠1与∠2互为邻补角的是( )
A. B. C. D.
【答案】C
【分析】根据邻补角的定义作出判断即可.
3.如图,已知直线AB、CD相交于点O,OE平分∠COB,若∠AOD=130°,则∠EOB度数是( )
A.65° B.50° C.25° D.130°
【答案】A
【点睛】此题主要考查了对顶角相等和角平分线的定义等知识,关键是掌握对顶角相等.
4.如图,AB、CD交于点O,若∠1=70°,射线OE平分∠AOC,那么∠EOD=__________度.
【答案】125
【点睛】本题主要考查了对顶角相等,角平分线的定义,平角的定义,正确求出∠AOD和∠AOE的度数是解题的关键.
5.如图,直线AB与CD相交于点O,∠BOC+∠AOD=288°,那么∠BOC的邻补角是_____度.
【答案】36
【分析】先根据对顶角相等求出∠BOC的度数,再利用邻补角的和等于180°列式计算即可.
6.如图,已知直线AB、CD相交于点O,如果∠AOC=70°,∠BOE:∠EOD=2:3,那么∠EOD的度数是______.
【详解】解:∵∠AOC=∠BOD,∠AOC=70°,
∴∠BOD=70°,
∵∠BOE:∠EOD=2:3,∠BOE+∠EOD=∠BOD,
∴∠EOD=∠BOD=×70°=42°
故答案为:42°.
7.直线AB、CD相交于点O,OE平分∠AOC,射线OF⊥CD于O点,且∠FOE=115°,求∠AOD的度数.
【详解】解:∵OF⊥CD于O点,
∴∠COF=90°
∵∠FOE=115°,
∴∠COE=∠FOE-∠COF=115°-90°=25°,
∵OE平分∠AOC,∠COE=25°,
∴∠AOC=2∠COE=50°,
∴∠AOD=180°-∠AOC=130°.
8.如图,O是直线AB上一点,OD平分∠AOC.
(1)若∠AOC=50°,请求出∠AOD的度数;
(2)若∠AOD和∠DOE互余,且∠AOD=,请求出∠BOC的度数.
(1)
解:∵∠AOC=50°,OD平分∠AOC,
∠AOD=25°
(2)
解:∵∠AOD和∠DOE互余,
∴∠AOE=∠AOD+∠DOE=90°
∴∠AOD=∠AOE=30°,
∵OD平分∠AOC,
∴∠AOC=2∠AOD=60°,
∠BOC=180°-∠AOC=120°
课堂总结
角的 名称 特 征 性 质 相 同 点 不 同 点
对 顶 角
邻 补 角 对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对
①有无公共边;
