新版北师大版七年级数学下册第二章相交线与平行线导学案
文档属性
| 名称 | 新版北师大版七年级数学下册第二章相交线与平行线导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-25 09:38:59 | ||
图片预览




文档简介
第二章 相交线与平行线
第一节 两条直线的位置关系(1)
【学习目标】
1.在具体情境中了解余角与补角,知道余角和补角的性质,通过练习掌握余角和补角的概念及性质,并能运用它们解决一些简单的实际问题。
2.经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理地表达的能力;经历探索余角、补角、对顶角的性质的过程。
3.通过学生动手操作、观察、合作、交流,进一步感受学习数学的意义,培养其主动探索、合作以及解决问题的能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】掌握余角、补角和对顶角的概念,性质及应用。
【学习过程】
模块一 预习反馈
一.学习准备
观察下面几幅生活中的图片:
1.在同一平面内,两条直线的位置关系有 和 两种
2.在同一平面内,不相交的两条直线叫做__________.
3.若两条直线只有一个公共点,我们称这两条直线为 .
二、教材精读
(1)如果将剪刀的图简单的表示为图2-1,那么∠1与∠2的位置有什么关系?它们的大小有什么关系?能试着说明,你的理由吗?
解: ,即 ,
,等式两边同时都减去_____________, ,,得: 。
归纳:在图2-1中,直线AB与CD相交于点O,的有一个公共点O,它们的两边互为反向延长线,具有这种位置关系的两个角叫 。
(2)在图2-1中,有什么数量关系?
解:由可知
总结: 如果两个角的和是,那么称这两个角互为补角.
类似的,如果两个角的和是,那么称这两个角互为余角.
注意:互余和互补是指两个角的数量关系,与它们的位置无关。
模块二 合作探究
如图2-2,打台球时,选择适当的方向用白球击打红球,反弹的红球会直接入袋,此时
将图2-2抽象成成图2-3,ON与DC交于点O,∠DON=∠CON=,∠1=∠2。在图2-3中:
(1):哪些角互为补角?哪些角互为余角?
(2):∠3与∠4有什么关系?为什么?
(3):∠AOC与∠BOD有什么关系?为什么? 你还能得到哪些结论?
解:(1)互为补角的如
(2)相等,
,
(3)
,
且
结论归纳:同角或等角的 相等,同角或等角的 相等。
模块三 形成提升
1.判断下列说法是否正确
(1)300 ,700 与800 的和为平角,所以这三个角互余。( )
(2)一个角的余角必为锐角。 ( )
(3)一个角的补角必为钝角。 ( )
(4)900 的角为余角。 ( )
两角是否互补既与其大小有关又与其位置有关( )
总结提示:互余与互补是指两个角之间的数量关系,与它们的位置关系无关。
2.下图中有对顶角吗?若有,请指出,若没有,请说明理由。
3. 如图,∠AOC+∠DOE+∠BOF= .
4. 的余角等于32°,则的补角等于 .
模块四 小结反思
本课知识
对顶角有如下性质对顶角
如果两个角的和是,那么称这两个角互为
如果两个角的和是,那么称这两个角互为
同角或等角的 相等,同角或等角的 相等。
二、我的困惑:
第一节 两条直线的位置关系 (2)
【学习目标】
1.使学生理解垂线的意义和垂线的第一个性质.
2.会用三角板过一点画已知直线的垂线,培养学生掌握画图的基本技能.
3.通过垂线性质的教学,培养学生发现问题的能力.
【学习方法】自主探究与合作交流相结合
【学习重点】会用工具按要求画垂线,掌握垂线(段)的性质.
【学习难点】从实际生活中感知垂线的性质以及体会点到直线的距离的意义,并能用准确的数学语言加以描述.
【学习过程】
模块一 预习反馈
一.学习准备
1.观察下列图片,你能找出其中相交的线吗?它们有什么特殊的位置关系?
______________________________________________________________________
______________________________________________________________________
2. 垂直的概念:两条直线相交成四个角,如果有一个角是______,那么称这两条直线互相______,其中一条直线叫做另一条直线的垂线,它们的交点叫做________。
3.垂直的表示:
如图2-4,如果用AB,CD表示两条互相垂直的直线,可以记作______;如图2-5如果用AB,CD表示两条互相垂直的直线,可以记作______,其中点O是垂足.
二.教材精读
如图2-6,点A在直线上,过点A画直线的垂线,你能画出多少条?如果点A在直线外呢?
如图2-7,点P是直线外一点,PO⊥,O是垂足,A,B,C在直线上,比较线段PO、PA、PB、PC的长短,你发现了什么?
解:(1)无论点A在直线上,还是直线外,过点A均只能画 条的垂线。
(2) 最短
归纳总结:①平面内,过一点有且只有一条直线与已知直线
②直线外一点与直线上各个点连接的所有 中, 最短
(3)如图2-8,过点A做的垂线,垂足为B,线段AB的
长度叫做点A到直线的____________。
模块二 合作探究
(1)如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?说说你的画法和理由
(2)你能借助三角尺,在一张白纸上画出两条互相垂直的直线吗?
你能用折纸的方法折出互相垂直的直线吗,试试看吧!
(4)如图,如何测量跳远成绩?
模块三 形成提升
1.下列说法中,正确的个数有( )
①有且只有一条直线与已知直线垂直②两条直线相交,一定垂直③若两条直线相交所形成的四个角相等,则这两条直线垂直A、1个 B、2个 C、3个 D、0个
2.到直线l的距离等于5cm的点有 ( )
A、2个 B、1个 C、无数个 D、无法确定
3.如图,AD⊥BD,BC⊥CD AB=m,BC=n,
则BD的取值范围是 ( )
A、BD>m B、BD模块四 小结反思
本课知识
1.两条直线相交成四个角,如果有一个角是________,那么称这两条直线互相_________,其中一条直线叫做另一条直线的垂线,它们的交点叫做___________。
2.如果用a,b表示两条互相垂直的直线,可以记作 ,
如果用AB,CD表示两条互相垂直的直线,可以记作 ,其中点O是垂足.
3. ①平面内,过一点有且只有一条直线与已知直线 。
②直线外一点与直线上各个点连接的所有 中 最短
二、我的困惑:
第二节 探索直线平行的条件 (1)
【学习目标】
1.通经历探索直线平行条件的过程,掌握利用同位角相等判别直线平行的结论,并能解决一些问题。
2.会识别由“三线八角”构成的同位角,会用三角尺过已知直线外一点画这条直线的平行线。
3.经历观察、操作、想象、推理、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】掌握利用同位角相等判别直线平行的结论,并能解决一些问题。
【学习过程】
模块一 预习反馈
学习准备
1.(1)在同一平面内两条直线的位置关系有 几种?分别是什么?
(2)如图2-9,两条直线相交所构成的四个角中分别有何关系?
2.装修工人如图2-10正在向墙上钉木条。如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角是多少度时,才能使木条a与木条b平行?
解:当木条a与墙壁边缘所夹角是 度时,木条a与木条b_______。
二、教材精读
1.如图,三根木条相交成∠1, ∠2,固定木条b,c,转动木条a
当∠1>∠2时 当∠1=∠2时 当∠1<∠2时
①直线a和b不平行 ②直线__________ ③直线____________
认识“三线八角”:两条直线被第三条直线所截,形成“三线八角”,具有∠1
与∠2这样位置关系的角称为同位角
①∠1和∠2是同位角
②∠3和∠4是
③∠5和 是同位角
④ 和∠8是同位角
注意: 同位角在被截直线的同一侧,在截线的同一方
判定两条直线平行的方法:两条直线被第三条直线所截,如果同位角相等,那么这两条直线 。 简称: 相等,两直线平行。
用符号“____”表示,例如,直线a与直线b平行,记作_______。
实践练习:如图2-12:因为∠1=∠2根据 相等,两直线平行
所以 ∥b
模块二 合作探究
你能过直线AB外一点P画直线AB的平行线吗?能画出几条?
在图2-13中,分别过点C,D画直线AB的平行线EF,GH,那么EF与GH又怎么样的位置关系?
解:(1)能过直线AB外一点画直线AB的平行线,只能画 条
(2)EF GH
归纳总结:①过直线外一点有且只有 直线与这条直线平行
②平行于同一直线的两条直线
实践练习:如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗 为什么
解:
//
又且
(同角的的补角相等)
( )
// (平行于同一直线的两直线平行)
模块三 形成提升
1.b∥a , c∥a , 那么 ,理由:
2.如右图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断______∥______,根据是_______________________.
(2)由∠CBE=∠C可以判断______∥______,根据是_________.
3. 如图所示,请写出能够得到直线AB∥CD的所有直接条件.
模块四 小结反思
本课知识
1.判定两条直线平行的方法:两条直线被第三条直线所截,如果同位角相等,那么这两条直线 ,简称: 相等,两直线平行。
2.①过直线外一点有且只有 直线与这条直线平行。
②平行于同一直线的两条直线 。
我的困惑:
探索直线平(2)
【学习目标】
会识别由“三线八角”构成的内错角合同旁内角。
2、经历探索直线平行条件的过程,掌握利用内错角相等、同旁内角互补判别直线平行的结论,并能解决一些问题。
3、经历观察、操作、想象、图利、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】
掌握利用内错角相等、同旁内角互补判别直线平行的结论,并能解决一些问题。
【学习过程】
模块一 预习反馈
一、学习准备
1.如图2-14,直线 a,b被直线c所截.
(1)数一数图中有几个角(不含平角)?
(2)写出图中的所有同位角,并用自己的语言说明什么样的角是同位角?
(3)同位角具备什么关系能够判断直线a∥b?你的依据是什么?
解:(1)图中有 个角
(2)同位角有 , , , ,
(3)只要(2)中任意一组同为角 ,a//b,依据是 .
教材精读
1. 图2-15中∠3与∠5,∠4与∠6这样位置关系的角有什么特点?说说你的理由。
解:∠3与∠5,∠4与∠6这样位置关系的角,在两条被截直线的 部,在截线的 侧,位置是交错的,这样的角叫做内错角。
2. 图2-15中∠3与∠6,∠4与∠5这样位置关系的角呢?说说你的理由。
解:∠3与∠6,∠4与∠5这样位置关系的角,在两条被截直线的 部,在截线的 ,这样的角叫做同旁内角。
实践练习:1.观察右图并填空:
(1)∠1 与 是同位角;
(2)∠5 与∠3是 角;
(3)∠1 与 是内错角.
2. 如图,直线AB,CD被EF所截,构成了八个角,你能找出哪些角是同位角、内错角、同旁内角吗?
解:同位角有 和
内错角有 和
同旁内角 和
3.(1)内错角满足什么关系时?两直线平行?为什么?
_____________________________________________________________________
(2)同旁内角满足什么关系时?两直线平行?为什么?
______________________________________________________________________
4. 看图填空:
解:(1)∠1 = ∠2(已知)
∠1 = ∠3(对顶角 )
∠3 = (等量代换)
直线 a∥ ( 相等,两直线平行)
(2)∵ ∠1 与∠2 (已知)
∠1 与∠3是 (邻补角定义)
∴ ∠3 = (同角的 相等)
∴ 直线 a b. ( )
归纳总结:内错角相等 相等 两直线平行
内错角相等 两直线平行
同旁内角互补
同位角相等 两直线平行
模块二 合作探究
1.做一做:你能用三块大小相同的三角板(30°,60°,90°)拼接成一个含有平行线段的图形吗 试一试,多拼几个图形,找出平行线段后,说明你的理由。
模块三 形成提升
1. 如图(1)∵∠A=_____(已知),
∴AC∥ED( )
(2)∵∠2=_____(已知),
∴AC∥ED( )
(3)∵∠A+_____=180°(已知),
∴AB∥FD( )
(4)∵∠A+_____=180°(已知),
∴DE∥AC( )
2.看图填空:
(1)如右图,∵∠1=∠2
∴ ∥ ,
∵∠2=
∴ ∥ ,同位角相等,两直线平行
∵∠3+∠4=180°
∴ ∥ ,( )
∴AC∥FG ( )
(2)如右图,∵∠2= ,
∴DE∥BC ( )
∵∠B+ =180°( )
∴DB∥EF
∵∠B+∠5=180°( )
∴ ∥ , ( )
3.如图,∠ABC=∠ADC,BF、DE是∠ABC、∠ ADC的角平分线,∠1=∠2.求证:DC∥AB.
模块四 小结反思
本课知识
1. 内错角相等 相等 两直线平行
相等
同旁内角互补
同位角相等 两直线平行
我的困惑:
第三节 平行线的性质(1)
【学习目标】
1.经历观察、操作、推理、交流等活动,了解平行线的性质,能运用这些性质进行简单的推理或计算。
2.经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理地表达的能力;经历探索平行线的特征的过程。
3.通过学生学习动手操作、观察、合作、交流,进一步感受学习数学的意义,培养其主动探索、合作以及解决问题的能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】平行线的性质,并能运用这些性质进行简单的推理或计算。
【学习过程】
模块一 预习反馈
一、学习准备
(1)因为∠1=∠5 (已知)
所以 a∥b( )
(2)因为∠4=∠ (已知)
所以a∥b(内错角相等,两直线平行 )
(3)因为∠4+∠ =1800 (已知)
所以a∥b( )
二、教材精读
直线a与直线b平行。
(1)测量同位角∠1和∠5的大小,它们有什么关系 图中还有其他的同位角吗?它们的大小有什么关系?
(2)图中有几对内错角?它们的大小有什么关系?为什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
(4)换另一组平行线试试,你能得到相同的结论吗?
解:(1)经测量∠1=∠5,图中还有同为角为:∠2和 , 和∠7, 和∠8,经测量他们都 .
(2)图中有 对内错角,他们都 。
理由:∠1=∠5 (已知)
∠1= (对顶角相等)
∴∠4= (等量代换)
同理可知∠3=
(3)图中有 对同旁内角,他们都 。
理由:∠1=∠5 (已知)
∠1+∠3= (邻补角定义)
∴ +∠3=(等量代换)
同理可知∠4+ =
(4)能得到相同的结论
归纳总结:性质1:两条平行直线被第三条直线所截, 相等。
简称:两直线平行, 同位角相等.
性质2:两条平行直线被第三条直线所截,内错角相等。
简称:两直线平行, 相等.
性质3:两条平行直线被第三条直线所截, 互补。
简称:两直线平行, 互补.
模块二 合作探究
1.如图所示,一束平行光线AB与DE 射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4。(1)∠1 ,∠3的大小有什么关系?∠ 2与∠4呢?(2)反射光线BC与EF也平行吗?
解:∵AB//DE(已知)
∴∠1= ( )
又∵∠1=∠2( )
∴∠2= ( 代换)
又∵∠3=∠4(已知)
∴∠2= (等量代换)
∴BC//EF ( )
模块三 形成提升
1.如图
∵ AD//BC (已知)
∴ ∠B=∠1 ( )
∵ AB//CD (已知)
∴ ∠D=∠1 ( )
∵ AD//BC (已知)
∴ ∠BCD+_______=180 ( )
2.当一个角的两边与另一个角的两边分别平行时,这两个角会是什么关系呢?试探究下列问题:(1)如图(1)所示, AB∥ED, BC∥EF,那么∠B与∠E的
关系是______(2)如图(2),AB∥ED, BC∥EF,那么∠B与∠E的关系是
。总结上面的结论是________________________________
模块四 小结反思
一、本课知识
1:两条平行直线被第三条直线所截, 相等。
简称:两直线平行, 同位角 相等.
2:两条平行直线被第三条直线所截,内错角相等。
简称:两直线平行, 相等.
3:两条平行直线被第三条直线所截, 互补。
简称:两直线平行, 互补.
我的反思:____________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
第三节 平行线的性质(2)
编者:唐道喜
【学习目标】
1.会利用平行线的特征解决一些简单的问题;
2.学会几何简单推理过程的书写。
【学习方法】自主探究与合作交流相结合
【学习重难点】平行线的性质,并能运用这些性质进行简单的推理或计算。
【学习过程】
模块一 预习反馈
一、学习准备
1.平行线的性质有哪几条?
2.判别直线平行的条件有哪几个?你现在一共有几个判定直线平行的方法?
解:(1)平行线的性质1:两条平行直线被第三条直线所截, 相等。
性质2:两条平行直线被第三条直线所截,内错角相等。
性质3:两条平行直线被第三条直线所截, 互补。
判别直线平行的条件有
同位角相等
内错角 两直线平行
同旁内角
二、教材精读
1. 如图:(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
解:(1)∵∠1=∠2( )
∴BF// ( )
(2)∵∠1=∠2( )
∴BF// ( )
(3)∵∠2=∠M( )
∴BF// ( )
2.如图所示:AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由。
解: ∵∠1 = ∠2 ( )
∴ EF∥ ( )
又∵AB∥CD( )
∴ ∥ (__________ )
3.已知直线a∥b,直线c∥d, ∠1=110°,求∠2,∠3的度数。
解:∵a∥b,且∠1=110°(已知)
∴ ∠2 = ∠1 =
∵c∥d( __________ )
∴∠1 + ∠3 = ( )
∴ ∠3 = 180°- (等式的基本性质)
= 180°-110°
=
实践练习:如图,选择合适的内容填空。
(1) ∵AB//CD
∴ =∠2( )
(2) ∵∠3=∠1
∴ // (同位角相等,两直线平行)
(3) ∵∠1+ =180
∴AB//CD( )
模块二 合作探究
1.如图,平行直线AB,CD被直线EF所截,分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线 ,问:GH和MN平行吗?请说明理由。
解:∵AB//CD( )
∴∠EGB= ( )
∵GH和MN分别是∠EGB和∠EMD的角平分线 (已知)
∴∠EGH= ∠EGB
且∠EMN=
∴∠EGH=∠EMN
∴ // (同位角相等, )
模块三:形成提升
1.填空
(1)如图,∵AC∥ED(已知)
∴∠A=_____( )
(2)如图,∵AC∥ED(已知)
∴∠EDF=_____( )
(3)如图,∵AB∥FD(已知)
∴∠A+____ =1800( )
(4)如图,∵AB∥FD(已知)
∴∠EDF+____=1800( )
(5)如图,∵BD∥EC(已知)
∴∠DBA=_____( ___________ __ )
∵∠C=∠D (已知)
∴∠DBA=______( )
∴FD∥_____( )
∴∠A=∠F ( )
2.如图所示,已知AD//BC,∠DBC与∠C互余,BD平分∠ABC,如果∠A=1120,那么∠ABC的度数是多少?∠C的度数呢?
模块四 小结反思
本课知识
1.同位角相等,两直线 . 2.内错角 ,两直线平行.
3.同旁内角 ,两直线平行. 4.两直线平行, 同位角 相等.
5.两直线平行, 相等. 6.两直线平行, 互补.
二、我的困惑:
第四节 用尺规作线段和角
【学习目标】
1.会利用尺规作一条线段等于已知线段,并能了解尺规作图中的简单应用。能利用尺规作线段的和、差。
2.能按照作图语言来完成作图动作,能用尺规作一个角等于已知角,并了解它在尺规作图中的简单应用。能利用尺规作角的和、差、倍。
3.在尺规作图过程当中,积累数学活动经验,培养动手能力和逻辑分析能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】用尺规作一条线段等于已知线段,及简单的应用。
【学习过程】
模块一 预习反馈
学习准备
1.已知:线段AB.
求作:线段A’B’,使A’B’=AB.
作法:(1)做一条射线A’C
(2)用圆规在 截取A’B’=
线段A’B’就是所求作的
教材精读
1.如图2—23,要在长方形木板上截一个平
行四边形,使它的一组对边在长方形木板
的边缘上,另一组对边中的一条边为AB。
(1)请过C点画出与AB平行的另一条边
(2)如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?
解:(1)“过直线外一点作已知直线的平行线”
(2)相当于 “过点C作∠ECD等于已知∠CAB.”
“作一个角等于已知角”
已知: ∠AOB。求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
作法:(1) 作射线O’A’;
(2) 以点O为圆心,任意长为 画
弧交OA于点C,交OB于点D;
(3) 以点O’为圆心,同样 长为半径
画弧交O’A’于点C’;
(4) 以点C’为圆心, 长为 画弧,交前面的弧于点D’ ,
(5) 过点D’作射线O’B’.
模块二 合作探究
1、如右图,已知线段a 和两条互相垂直的直线AB,CD。
(1)利用圆规,在射线OA,OB,OC,OD上作线段OA’,OB’,OC’,OD’,使它们分别与线段a 相等。
(2) 依次连接A’,C’ ,B’,D’,A’.
你得到了一个怎样的图形?与同伴进行交流。
______________________________________
____________________________
模块三 形成提升
1.如图,已知线段a和b,直线AB与CD垂直且相交于点O.
利用尺规,按下列要求作图:
(1)在射线OA , OB , OC上作线段O A’,OB’ ,OC’,使它们分别与线段a 相等;
(2) 在射线OD上作线段OD’,使OD’等于b;
(3) 依次连接A’,C’,B’,D’,A’.
你得到了一个怎样的图形?与同伴进行交流.
_______________________________________
_____________________________________________________________________
2.已知:如图∠α, ∠β
求作: ∠AOB,使得∠AOB= ∠α-∠β
模块四 小结反思
一、本课知识点:
二、我的困惑:
第二章《平行线与相交线》
回顾与思考
【学习目标】
1.掌握平行线与相交线的相关知识,梳理本章内容,建立一定的知识体系;并能够综合运用这些知识解决相关的问题。
2.在丰富的情景中,抽象出平行线、相交线等几何模型,通过讨论角与角之间的关系,进一步认识平行线和相交线。
3.在认识操作基础上锻炼学生的语言表达能力以及逻辑思维能力。
【学习方法】小组合作学习
【学习重难点】
1、掌握本单元的知识点,建立知识体系。
2、多角度地了解平行线与相交线的性质和证明。
【学习过程】
模块一
1.展示自己的知识网络图
2.方法总结:
模块二
典型例题
1. 如图,已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,请说明:AE⊥CF.
2. 如图,已知,求的度数.
3.如图,已知∠EFB+∠ADC=180°,且∠1=∠2,试说明DG∥AB.
4.已知∠AOB及两边上的点M、N(如图)请用尺规分别过点M、N作OB、OA的平行线,不写作法,保留作图痕迹。
模块三 形成提升
2.如图,BC∥DE,小颖用量角器分别画出∠ABC、∠ADE的角平分线BG、DH,想一想,小颖所画的这两条射线BG和DH会平行吗?为什么?(请你先用量角器画出这两条角平分线)
对顶角有如下性质:
对顶角
2
D
C
O
1
3
4
A
N
B
图2-3
图2-2
H
G
F
E
D
C
B
A
图2-13
b
a
2
3
1
C
A
B
D
1
(角平分线定义)
第一节 两条直线的位置关系(1)
【学习目标】
1.在具体情境中了解余角与补角,知道余角和补角的性质,通过练习掌握余角和补角的概念及性质,并能运用它们解决一些简单的实际问题。
2.经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理地表达的能力;经历探索余角、补角、对顶角的性质的过程。
3.通过学生动手操作、观察、合作、交流,进一步感受学习数学的意义,培养其主动探索、合作以及解决问题的能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】掌握余角、补角和对顶角的概念,性质及应用。
【学习过程】
模块一 预习反馈
一.学习准备
观察下面几幅生活中的图片:
1.在同一平面内,两条直线的位置关系有 和 两种
2.在同一平面内,不相交的两条直线叫做__________.
3.若两条直线只有一个公共点,我们称这两条直线为 .
二、教材精读
(1)如果将剪刀的图简单的表示为图2-1,那么∠1与∠2的位置有什么关系?它们的大小有什么关系?能试着说明,你的理由吗?
解: ,即 ,
,等式两边同时都减去_____________, ,,得: 。
归纳:在图2-1中,直线AB与CD相交于点O,的有一个公共点O,它们的两边互为反向延长线,具有这种位置关系的两个角叫 。
(2)在图2-1中,有什么数量关系?
解:由可知
总结: 如果两个角的和是,那么称这两个角互为补角.
类似的,如果两个角的和是,那么称这两个角互为余角.
注意:互余和互补是指两个角的数量关系,与它们的位置无关。
模块二 合作探究
如图2-2,打台球时,选择适当的方向用白球击打红球,反弹的红球会直接入袋,此时
将图2-2抽象成成图2-3,ON与DC交于点O,∠DON=∠CON=,∠1=∠2。在图2-3中:
(1):哪些角互为补角?哪些角互为余角?
(2):∠3与∠4有什么关系?为什么?
(3):∠AOC与∠BOD有什么关系?为什么? 你还能得到哪些结论?
解:(1)互为补角的如
(2)相等,
,
(3)
,
且
结论归纳:同角或等角的 相等,同角或等角的 相等。
模块三 形成提升
1.判断下列说法是否正确
(1)300 ,700 与800 的和为平角,所以这三个角互余。( )
(2)一个角的余角必为锐角。 ( )
(3)一个角的补角必为钝角。 ( )
(4)900 的角为余角。 ( )
两角是否互补既与其大小有关又与其位置有关( )
总结提示:互余与互补是指两个角之间的数量关系,与它们的位置关系无关。
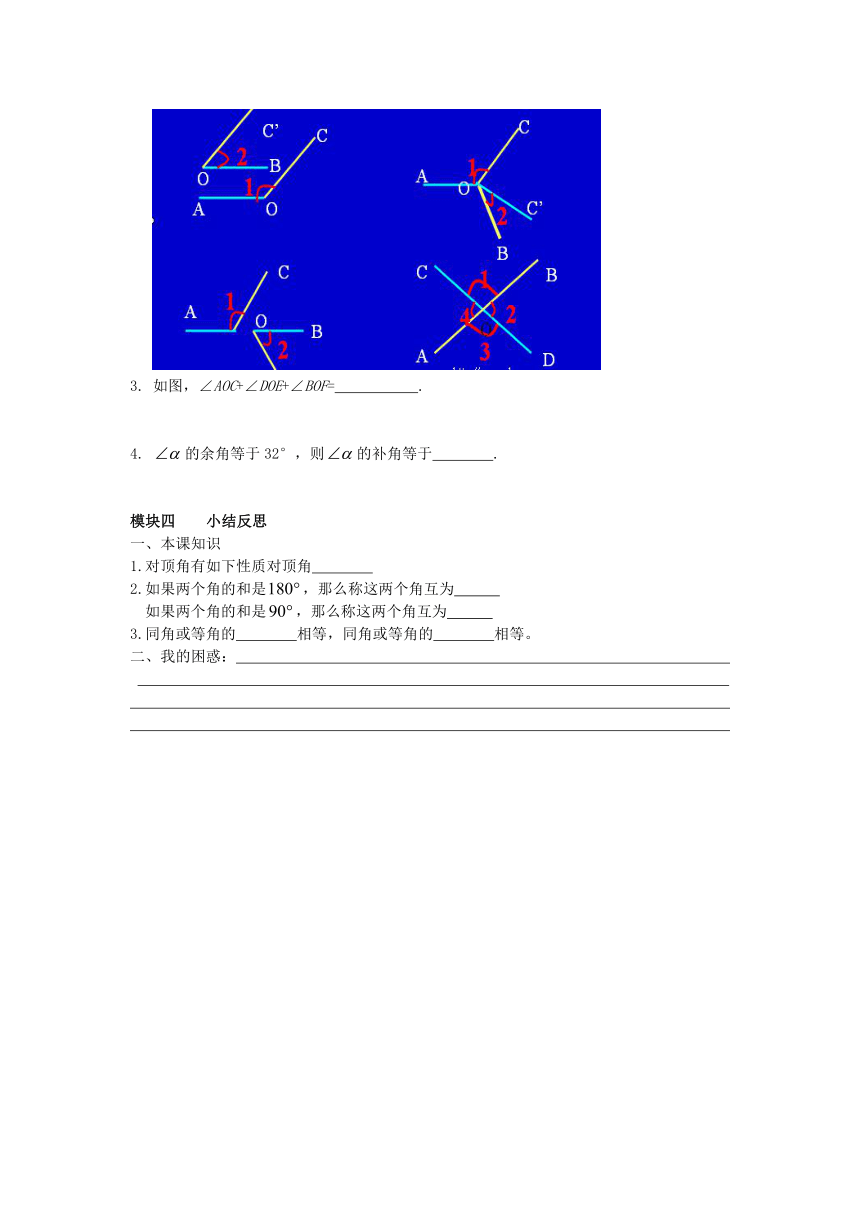
2.下图中有对顶角吗?若有,请指出,若没有,请说明理由。
3. 如图,∠AOC+∠DOE+∠BOF= .
4. 的余角等于32°,则的补角等于 .
模块四 小结反思
本课知识
对顶角有如下性质对顶角
如果两个角的和是,那么称这两个角互为
如果两个角的和是,那么称这两个角互为
同角或等角的 相等,同角或等角的 相等。
二、我的困惑:
第一节 两条直线的位置关系 (2)
【学习目标】
1.使学生理解垂线的意义和垂线的第一个性质.
2.会用三角板过一点画已知直线的垂线,培养学生掌握画图的基本技能.
3.通过垂线性质的教学,培养学生发现问题的能力.
【学习方法】自主探究与合作交流相结合
【学习重点】会用工具按要求画垂线,掌握垂线(段)的性质.
【学习难点】从实际生活中感知垂线的性质以及体会点到直线的距离的意义,并能用准确的数学语言加以描述.
【学习过程】
模块一 预习反馈
一.学习准备
1.观察下列图片,你能找出其中相交的线吗?它们有什么特殊的位置关系?
______________________________________________________________________
______________________________________________________________________
2. 垂直的概念:两条直线相交成四个角,如果有一个角是______,那么称这两条直线互相______,其中一条直线叫做另一条直线的垂线,它们的交点叫做________。
3.垂直的表示:
如图2-4,如果用AB,CD表示两条互相垂直的直线,可以记作______;如图2-5如果用AB,CD表示两条互相垂直的直线,可以记作______,其中点O是垂足.
二.教材精读
如图2-6,点A在直线上,过点A画直线的垂线,你能画出多少条?如果点A在直线外呢?
如图2-7,点P是直线外一点,PO⊥,O是垂足,A,B,C在直线上,比较线段PO、PA、PB、PC的长短,你发现了什么?
解:(1)无论点A在直线上,还是直线外,过点A均只能画 条的垂线。
(2) 最短
归纳总结:①平面内,过一点有且只有一条直线与已知直线
②直线外一点与直线上各个点连接的所有 中, 最短
(3)如图2-8,过点A做的垂线,垂足为B,线段AB的
长度叫做点A到直线的____________。
模块二 合作探究
(1)如果只有直尺,你能在方格纸上画出两条互相垂直的直线吗?说说你的画法和理由
(2)你能借助三角尺,在一张白纸上画出两条互相垂直的直线吗?
你能用折纸的方法折出互相垂直的直线吗,试试看吧!
(4)如图,如何测量跳远成绩?
模块三 形成提升
1.下列说法中,正确的个数有( )
①有且只有一条直线与已知直线垂直②两条直线相交,一定垂直③若两条直线相交所形成的四个角相等,则这两条直线垂直A、1个 B、2个 C、3个 D、0个
2.到直线l的距离等于5cm的点有 ( )
A、2个 B、1个 C、无数个 D、无法确定
3.如图,AD⊥BD,BC⊥CD AB=m,BC=n,
则BD的取值范围是 ( )
A、BD>m B、BD
本课知识
1.两条直线相交成四个角,如果有一个角是________,那么称这两条直线互相_________,其中一条直线叫做另一条直线的垂线,它们的交点叫做___________。
2.如果用a,b表示两条互相垂直的直线,可以记作 ,
如果用AB,CD表示两条互相垂直的直线,可以记作 ,其中点O是垂足.
3. ①平面内,过一点有且只有一条直线与已知直线 。
②直线外一点与直线上各个点连接的所有 中 最短
二、我的困惑:
第二节 探索直线平行的条件 (1)
【学习目标】
1.通经历探索直线平行条件的过程,掌握利用同位角相等判别直线平行的结论,并能解决一些问题。
2.会识别由“三线八角”构成的同位角,会用三角尺过已知直线外一点画这条直线的平行线。
3.经历观察、操作、想象、推理、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】掌握利用同位角相等判别直线平行的结论,并能解决一些问题。
【学习过程】
模块一 预习反馈
学习准备
1.(1)在同一平面内两条直线的位置关系有 几种?分别是什么?
(2)如图2-9,两条直线相交所构成的四个角中分别有何关系?
2.装修工人如图2-10正在向墙上钉木条。如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角是多少度时,才能使木条a与木条b平行?
解:当木条a与墙壁边缘所夹角是 度时,木条a与木条b_______。
二、教材精读
1.如图,三根木条相交成∠1, ∠2,固定木条b,c,转动木条a
当∠1>∠2时 当∠1=∠2时 当∠1<∠2时
①直线a和b不平行 ②直线__________ ③直线____________
认识“三线八角”:两条直线被第三条直线所截,形成“三线八角”,具有∠1
与∠2这样位置关系的角称为同位角
①∠1和∠2是同位角
②∠3和∠4是
③∠5和 是同位角
④ 和∠8是同位角
注意: 同位角在被截直线的同一侧,在截线的同一方
判定两条直线平行的方法:两条直线被第三条直线所截,如果同位角相等,那么这两条直线 。 简称: 相等,两直线平行。
用符号“____”表示,例如,直线a与直线b平行,记作_______。
实践练习:如图2-12:因为∠1=∠2根据 相等,两直线平行
所以 ∥b
模块二 合作探究
你能过直线AB外一点P画直线AB的平行线吗?能画出几条?
在图2-13中,分别过点C,D画直线AB的平行线EF,GH,那么EF与GH又怎么样的位置关系?
解:(1)能过直线AB外一点画直线AB的平行线,只能画 条
(2)EF GH
归纳总结:①过直线外一点有且只有 直线与这条直线平行
②平行于同一直线的两条直线
实践练习:如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗 为什么
解:
//
又且
(同角的的补角相等)
( )
// (平行于同一直线的两直线平行)
模块三 形成提升
1.b∥a , c∥a , 那么 ,理由:
2.如右图所示,BE是AB的延长线,量得∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断______∥______,根据是_______________________.
(2)由∠CBE=∠C可以判断______∥______,根据是_________.
3. 如图所示,请写出能够得到直线AB∥CD的所有直接条件.
模块四 小结反思
本课知识
1.判定两条直线平行的方法:两条直线被第三条直线所截,如果同位角相等,那么这两条直线 ,简称: 相等,两直线平行。
2.①过直线外一点有且只有 直线与这条直线平行。
②平行于同一直线的两条直线 。
我的困惑:
探索直线平(2)
【学习目标】
会识别由“三线八角”构成的内错角合同旁内角。
2、经历探索直线平行条件的过程,掌握利用内错角相等、同旁内角互补判别直线平行的结论,并能解决一些问题。
3、经历观察、操作、想象、图利、交流等活动,体会利用操作、归纳获得数学结论的过程,进一步发展空间想象、推理能力和有条理表达的能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】
掌握利用内错角相等、同旁内角互补判别直线平行的结论,并能解决一些问题。
【学习过程】
模块一 预习反馈
一、学习准备
1.如图2-14,直线 a,b被直线c所截.
(1)数一数图中有几个角(不含平角)?
(2)写出图中的所有同位角,并用自己的语言说明什么样的角是同位角?
(3)同位角具备什么关系能够判断直线a∥b?你的依据是什么?
解:(1)图中有 个角
(2)同位角有 , , , ,
(3)只要(2)中任意一组同为角 ,a//b,依据是 .
教材精读
1. 图2-15中∠3与∠5,∠4与∠6这样位置关系的角有什么特点?说说你的理由。
解:∠3与∠5,∠4与∠6这样位置关系的角,在两条被截直线的 部,在截线的 侧,位置是交错的,这样的角叫做内错角。
2. 图2-15中∠3与∠6,∠4与∠5这样位置关系的角呢?说说你的理由。
解:∠3与∠6,∠4与∠5这样位置关系的角,在两条被截直线的 部,在截线的 ,这样的角叫做同旁内角。
实践练习:1.观察右图并填空:
(1)∠1 与 是同位角;
(2)∠5 与∠3是 角;
(3)∠1 与 是内错角.
2. 如图,直线AB,CD被EF所截,构成了八个角,你能找出哪些角是同位角、内错角、同旁内角吗?
解:同位角有 和
内错角有 和
同旁内角 和
3.(1)内错角满足什么关系时?两直线平行?为什么?
_____________________________________________________________________
(2)同旁内角满足什么关系时?两直线平行?为什么?
______________________________________________________________________
4. 看图填空:
解:(1)∠1 = ∠2(已知)
∠1 = ∠3(对顶角 )
∠3 = (等量代换)
直线 a∥ ( 相等,两直线平行)
(2)∵ ∠1 与∠2 (已知)
∠1 与∠3是 (邻补角定义)
∴ ∠3 = (同角的 相等)
∴ 直线 a b. ( )
归纳总结:内错角相等 相等 两直线平行
内错角相等 两直线平行
同旁内角互补
同位角相等 两直线平行
模块二 合作探究
1.做一做:你能用三块大小相同的三角板(30°,60°,90°)拼接成一个含有平行线段的图形吗 试一试,多拼几个图形,找出平行线段后,说明你的理由。
模块三 形成提升
1. 如图(1)∵∠A=_____(已知),
∴AC∥ED( )
(2)∵∠2=_____(已知),
∴AC∥ED( )
(3)∵∠A+_____=180°(已知),
∴AB∥FD( )
(4)∵∠A+_____=180°(已知),
∴DE∥AC( )
2.看图填空:
(1)如右图,∵∠1=∠2
∴ ∥ ,
∵∠2=
∴ ∥ ,同位角相等,两直线平行
∵∠3+∠4=180°
∴ ∥ ,( )
∴AC∥FG ( )
(2)如右图,∵∠2= ,
∴DE∥BC ( )
∵∠B+ =180°( )
∴DB∥EF
∵∠B+∠5=180°( )
∴ ∥ , ( )
3.如图,∠ABC=∠ADC,BF、DE是∠ABC、∠ ADC的角平分线,∠1=∠2.求证:DC∥AB.
模块四 小结反思
本课知识
1. 内错角相等 相等 两直线平行
相等
同旁内角互补
同位角相等 两直线平行
我的困惑:
第三节 平行线的性质(1)
【学习目标】
1.经历观察、操作、推理、交流等活动,了解平行线的性质,能运用这些性质进行简单的推理或计算。
2.经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理地表达的能力;经历探索平行线的特征的过程。
3.通过学生学习动手操作、观察、合作、交流,进一步感受学习数学的意义,培养其主动探索、合作以及解决问题的能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】平行线的性质,并能运用这些性质进行简单的推理或计算。
【学习过程】
模块一 预习反馈
一、学习准备
(1)因为∠1=∠5 (已知)
所以 a∥b( )
(2)因为∠4=∠ (已知)
所以a∥b(内错角相等,两直线平行 )
(3)因为∠4+∠ =1800 (已知)
所以a∥b( )
二、教材精读
直线a与直线b平行。
(1)测量同位角∠1和∠5的大小,它们有什么关系 图中还有其他的同位角吗?它们的大小有什么关系?
(2)图中有几对内错角?它们的大小有什么关系?为什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
(4)换另一组平行线试试,你能得到相同的结论吗?
解:(1)经测量∠1=∠5,图中还有同为角为:∠2和 , 和∠7, 和∠8,经测量他们都 .
(2)图中有 对内错角,他们都 。
理由:∠1=∠5 (已知)
∠1= (对顶角相等)
∴∠4= (等量代换)
同理可知∠3=
(3)图中有 对同旁内角,他们都 。
理由:∠1=∠5 (已知)
∠1+∠3= (邻补角定义)
∴ +∠3=(等量代换)
同理可知∠4+ =
(4)能得到相同的结论
归纳总结:性质1:两条平行直线被第三条直线所截, 相等。
简称:两直线平行, 同位角相等.
性质2:两条平行直线被第三条直线所截,内错角相等。
简称:两直线平行, 相等.
性质3:两条平行直线被第三条直线所截, 互补。
简称:两直线平行, 互补.
模块二 合作探究
1.如图所示,一束平行光线AB与DE 射向一个水平镜面后被反射,此时∠1=∠2,∠3=∠4。(1)∠1 ,∠3的大小有什么关系?∠ 2与∠4呢?(2)反射光线BC与EF也平行吗?
解:∵AB//DE(已知)
∴∠1= ( )
又∵∠1=∠2( )
∴∠2= ( 代换)
又∵∠3=∠4(已知)
∴∠2= (等量代换)
∴BC//EF ( )
模块三 形成提升
1.如图
∵ AD//BC (已知)
∴ ∠B=∠1 ( )
∵ AB//CD (已知)
∴ ∠D=∠1 ( )
∵ AD//BC (已知)
∴ ∠BCD+_______=180 ( )
2.当一个角的两边与另一个角的两边分别平行时,这两个角会是什么关系呢?试探究下列问题:(1)如图(1)所示, AB∥ED, BC∥EF,那么∠B与∠E的
关系是______(2)如图(2),AB∥ED, BC∥EF,那么∠B与∠E的关系是
。总结上面的结论是________________________________
模块四 小结反思
一、本课知识
1:两条平行直线被第三条直线所截, 相等。
简称:两直线平行, 同位角 相等.
2:两条平行直线被第三条直线所截,内错角相等。
简称:两直线平行, 相等.
3:两条平行直线被第三条直线所截, 互补。
简称:两直线平行, 互补.
我的反思:____________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
第三节 平行线的性质(2)
编者:唐道喜
【学习目标】
1.会利用平行线的特征解决一些简单的问题;
2.学会几何简单推理过程的书写。
【学习方法】自主探究与合作交流相结合
【学习重难点】平行线的性质,并能运用这些性质进行简单的推理或计算。
【学习过程】
模块一 预习反馈
一、学习准备
1.平行线的性质有哪几条?
2.判别直线平行的条件有哪几个?你现在一共有几个判定直线平行的方法?
解:(1)平行线的性质1:两条平行直线被第三条直线所截, 相等。
性质2:两条平行直线被第三条直线所截,内错角相等。
性质3:两条平行直线被第三条直线所截, 互补。
判别直线平行的条件有
同位角相等
内错角 两直线平行
同旁内角
二、教材精读
1. 如图:(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
解:(1)∵∠1=∠2( )
∴BF// ( )
(2)∵∠1=∠2( )
∴BF// ( )
(3)∵∠2=∠M( )
∴BF// ( )
2.如图所示:AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由。
解: ∵∠1 = ∠2 ( )
∴ EF∥ ( )
又∵AB∥CD( )
∴ ∥ (__________ )
3.已知直线a∥b,直线c∥d, ∠1=110°,求∠2,∠3的度数。
解:∵a∥b,且∠1=110°(已知)
∴ ∠2 = ∠1 =
∵c∥d( __________ )
∴∠1 + ∠3 = ( )
∴ ∠3 = 180°- (等式的基本性质)
= 180°-110°
=
实践练习:如图,选择合适的内容填空。
(1) ∵AB//CD
∴ =∠2( )
(2) ∵∠3=∠1
∴ // (同位角相等,两直线平行)
(3) ∵∠1+ =180
∴AB//CD( )
模块二 合作探究
1.如图,平行直线AB,CD被直线EF所截,分别交直线AB,CD于点G,M。GH和MN分别是∠EGB和∠EMD的角平分线 ,问:GH和MN平行吗?请说明理由。
解:∵AB//CD( )
∴∠EGB= ( )
∵GH和MN分别是∠EGB和∠EMD的角平分线 (已知)
∴∠EGH= ∠EGB
且∠EMN=
∴∠EGH=∠EMN
∴ // (同位角相等, )
模块三:形成提升
1.填空
(1)如图,∵AC∥ED(已知)
∴∠A=_____( )
(2)如图,∵AC∥ED(已知)
∴∠EDF=_____( )
(3)如图,∵AB∥FD(已知)
∴∠A+____ =1800( )
(4)如图,∵AB∥FD(已知)
∴∠EDF+____=1800( )
(5)如图,∵BD∥EC(已知)
∴∠DBA=_____( ___________ __ )
∵∠C=∠D (已知)
∴∠DBA=______( )
∴FD∥_____( )
∴∠A=∠F ( )
2.如图所示,已知AD//BC,∠DBC与∠C互余,BD平分∠ABC,如果∠A=1120,那么∠ABC的度数是多少?∠C的度数呢?
模块四 小结反思
本课知识
1.同位角相等,两直线 . 2.内错角 ,两直线平行.
3.同旁内角 ,两直线平行. 4.两直线平行, 同位角 相等.
5.两直线平行, 相等. 6.两直线平行, 互补.
二、我的困惑:
第四节 用尺规作线段和角
【学习目标】
1.会利用尺规作一条线段等于已知线段,并能了解尺规作图中的简单应用。能利用尺规作线段的和、差。
2.能按照作图语言来完成作图动作,能用尺规作一个角等于已知角,并了解它在尺规作图中的简单应用。能利用尺规作角的和、差、倍。
3.在尺规作图过程当中,积累数学活动经验,培养动手能力和逻辑分析能力。
【学习方法】自主探究与合作交流相结合
【学习重难点】用尺规作一条线段等于已知线段,及简单的应用。
【学习过程】
模块一 预习反馈
学习准备
1.已知:线段AB.
求作:线段A’B’,使A’B’=AB.
作法:(1)做一条射线A’C
(2)用圆规在 截取A’B’=
线段A’B’就是所求作的
教材精读
1.如图2—23,要在长方形木板上截一个平
行四边形,使它的一组对边在长方形木板
的边缘上,另一组对边中的一条边为AB。
(1)请过C点画出与AB平行的另一条边
(2)如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?
解:(1)“过直线外一点作已知直线的平行线”
(2)相当于 “过点C作∠ECD等于已知∠CAB.”
“作一个角等于已知角”
已知: ∠AOB。求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
作法:(1) 作射线O’A’;
(2) 以点O为圆心,任意长为 画
弧交OA于点C,交OB于点D;
(3) 以点O’为圆心,同样 长为半径
画弧交O’A’于点C’;
(4) 以点C’为圆心, 长为 画弧,交前面的弧于点D’ ,
(5) 过点D’作射线O’B’.
模块二 合作探究
1、如右图,已知线段a 和两条互相垂直的直线AB,CD。
(1)利用圆规,在射线OA,OB,OC,OD上作线段OA’,OB’,OC’,OD’,使它们分别与线段a 相等。
(2) 依次连接A’,C’ ,B’,D’,A’.
你得到了一个怎样的图形?与同伴进行交流。
______________________________________
____________________________
模块三 形成提升
1.如图,已知线段a和b,直线AB与CD垂直且相交于点O.
利用尺规,按下列要求作图:
(1)在射线OA , OB , OC上作线段O A’,OB’ ,OC’,使它们分别与线段a 相等;
(2) 在射线OD上作线段OD’,使OD’等于b;
(3) 依次连接A’,C’,B’,D’,A’.
你得到了一个怎样的图形?与同伴进行交流.
_______________________________________
_____________________________________________________________________
2.已知:如图∠α, ∠β
求作: ∠AOB,使得∠AOB= ∠α-∠β
模块四 小结反思
一、本课知识点:
二、我的困惑:
第二章《平行线与相交线》
回顾与思考
【学习目标】
1.掌握平行线与相交线的相关知识,梳理本章内容,建立一定的知识体系;并能够综合运用这些知识解决相关的问题。
2.在丰富的情景中,抽象出平行线、相交线等几何模型,通过讨论角与角之间的关系,进一步认识平行线和相交线。
3.在认识操作基础上锻炼学生的语言表达能力以及逻辑思维能力。
【学习方法】小组合作学习
【学习重难点】
1、掌握本单元的知识点,建立知识体系。
2、多角度地了解平行线与相交线的性质和证明。
【学习过程】
模块一
1.展示自己的知识网络图
2.方法总结:
模块二
典型例题
1. 如图,已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,请说明:AE⊥CF.
2. 如图,已知,求的度数.
3.如图,已知∠EFB+∠ADC=180°,且∠1=∠2,试说明DG∥AB.
4.已知∠AOB及两边上的点M、N(如图)请用尺规分别过点M、N作OB、OA的平行线,不写作法,保留作图痕迹。
模块三 形成提升
2.如图,BC∥DE,小颖用量角器分别画出∠ABC、∠ADE的角平分线BG、DH,想一想,小颖所画的这两条射线BG和DH会平行吗?为什么?(请你先用量角器画出这两条角平分线)
对顶角有如下性质:
对顶角
2
D
C
O
1
3
4
A
N
B
图2-3
图2-2
H
G
F
E
D
C
B
A
图2-13
b
a
2
3
1
C
A
B
D
1
(角平分线定义)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
