9.3.1 面积类游戏第3课时 转盘类游戏同步练习(含答案)
文档属性
| 名称 | 9.3.1 面积类游戏第3课时 转盘类游戏同步练习(含答案) | 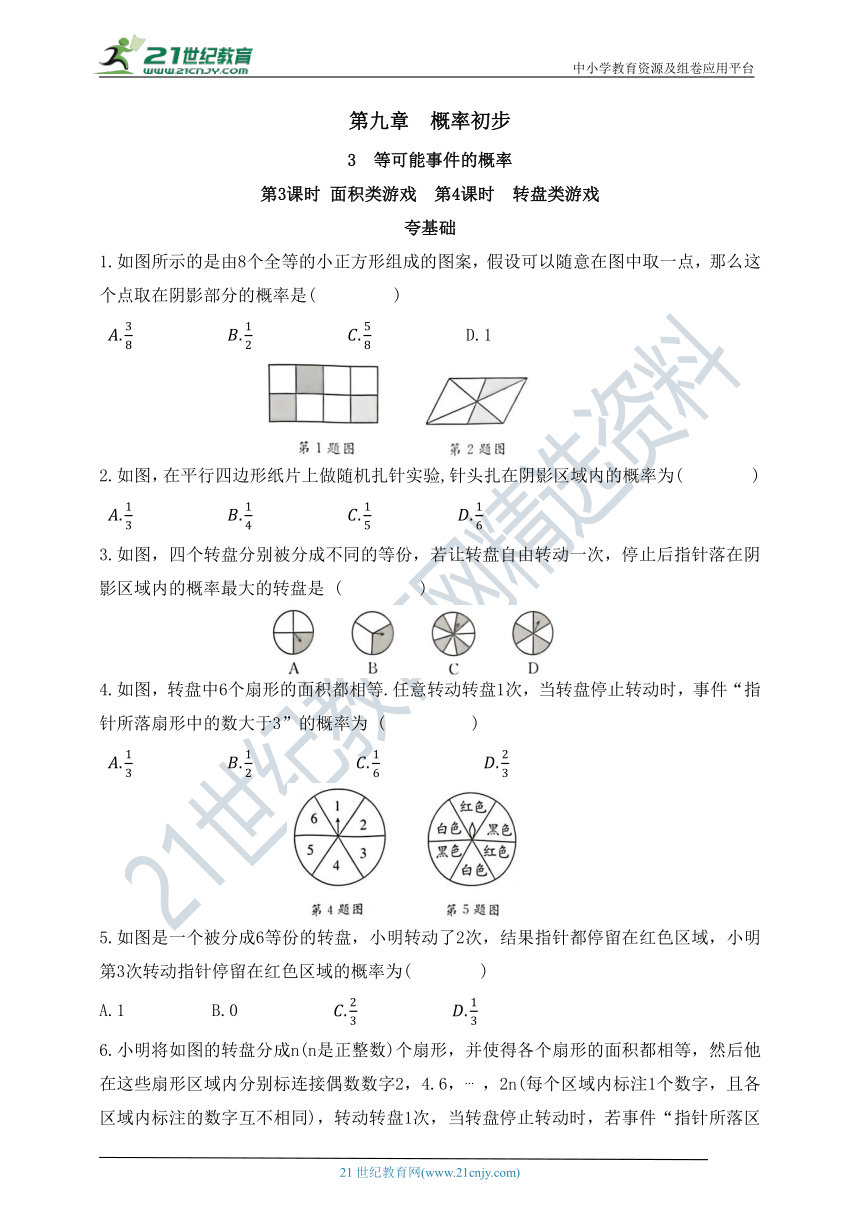 | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 11:06:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章 概率初步
3 等可能事件的概率
面积类游戏 第4课时 转盘类游戏
夸基础
1.如图所示的是由8个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是( )
D.1
2.如图,在平行四边形纸片上做随机扎针实验,针头扎在阴影区域内的概率为( )
3.如图,四个转盘分别被分成不同的等份,若让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是 ( )
4.如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,事件“指针所落扇形中的数大于3”的概率为 ( )
5.如图是一个被分成6等份的转盘,小明转动了2次,结果指针都停留在红色区域,小明第3次转动指针停留在红色区域的概率为( )
A.1 B.0
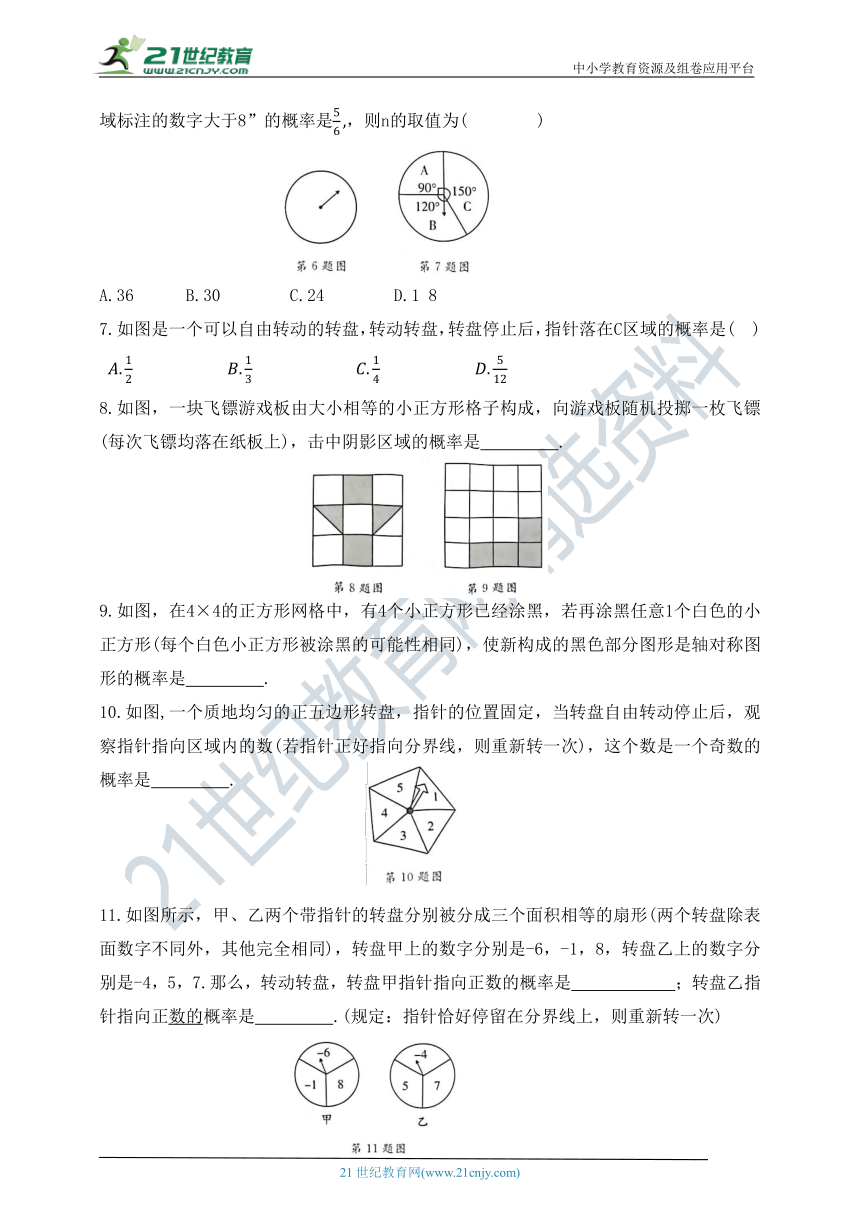
6.小明将如图的转盘分成n(n是正整数)个扇形,并使得各个扇形的面积都相等,然后他在这些扇形区域内分别标连接偶数数字2,4.6, ,2n(每个区域内标注1个数字,且各区域内标注的数字互不相同),转动转盘1次,当转盘停止转动时,若事件“指针所落区域标注的数字大于8”的概率是,则n的取值为( )
A.36 B.30 C.24 D.1 8
7.如图是一个可以自由转动的转盘,转动转盘,转盘停止后,指针落在C区域的概率是( )
8.如图,一块飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖(每次飞镖均落在纸板上),击中阴影区域的概率是 .
9.如图,在4×4的正方形网格中,有4个小正方形已经涂黑,若再涂黑任意1个白色的小正方形(每个白色小正方形被涂黑的可能性相同),使新构成的黑色部分图形是轴对称图形的概率是 .
10.如图,一个质地均匀的正五边形转盘,指针的位置固定,当转盘自由转动停止后,观察指针指向区域内的数(若指针正好指向分界线,则重新转一次),这个数是一个奇数的概率是 .
11.如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其他完全相同),转盘甲上的数字分别是-6,-1,8,转盘乙上的数字分别是-4,5,7.那么,转动转盘,转盘甲指针指向正数的概率是 ;转盘乙指针指向正数的概率是 .(规定:指针恰好停留在分界线上,则重新转一次)
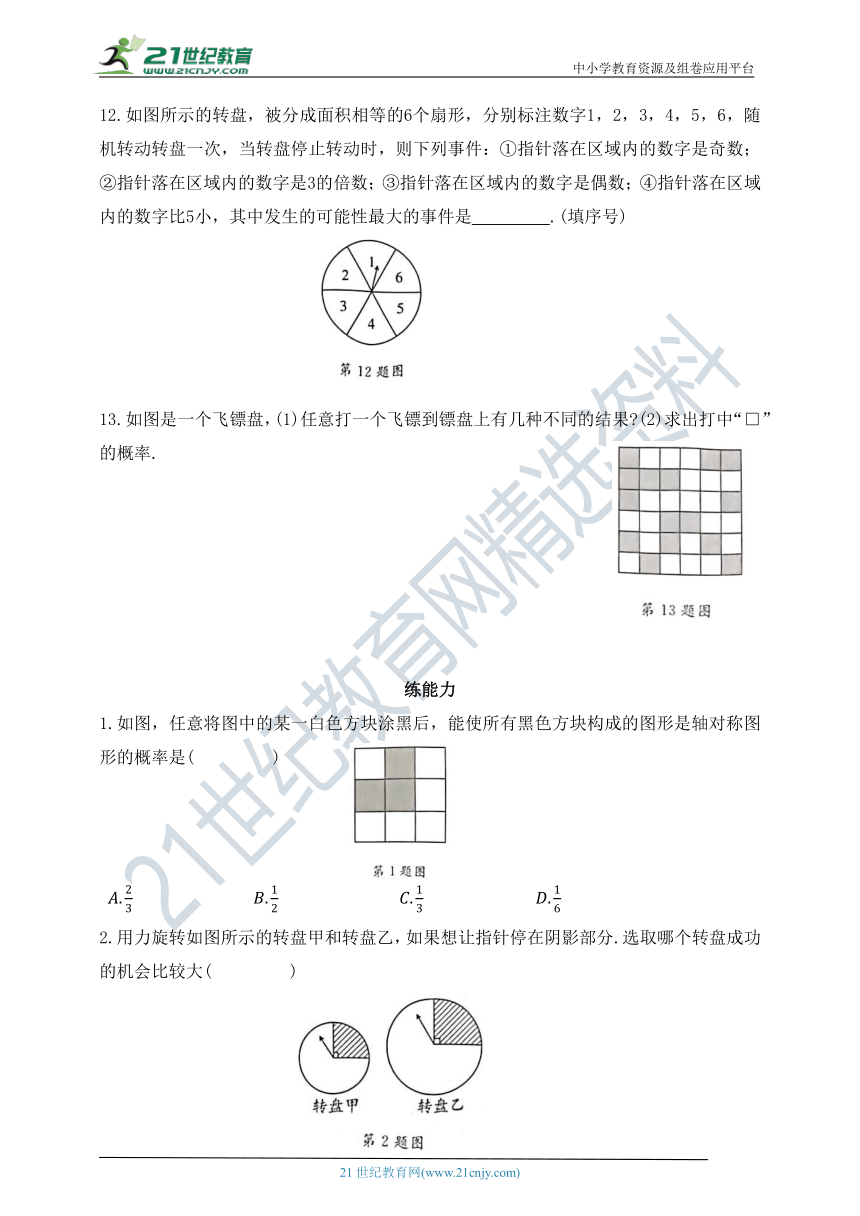
12.如图所示的转盘,被分成面积相等的6个扇形,分别标注数字1,2,3,4,5,6,随机转动转盘一次,当转盘停止转动时,则下列事件:①指针落在区域内的数字是奇数;②指针落在区域内的数字是3的倍数;③指针落在区域内的数字是偶数;④指针落在区域内的数字比5小,其中发生的可能性最大的事件是 .(填序号)
13.如图是一个飞镖盘,(1)任意打一个飞镖到镖盘上有几种不同的结果 (2)求出打中“□”的概率.
练能力
1.如图,任意将图中的某一白色方块涂黑后,能使所有黑色方块构成的图形是轴对称图形的概率是( )
2.用力旋转如图所示的转盘甲和转盘乙,如果想让指针停在阴影部分.选取哪个转盘成功的机会比较大( )
A.转盘甲 B.转盘乙 C.两个一样大 D.无法确定
3.如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是 ( )
4.如图,正方形ABCD及其内切圆O,随机地往正方形内投一粒米,落在阴影部分的概率是( )
5.以下转盘分别被分成2个,4个,5个,6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是则对应的转盘是( )
6[2021·安徽]如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是( )
7.分别向如图所示的四个区域投掷一个小球,小球落在阴影部分的概率最小的是( )
8.如图所示,镖盘为两个半径为1:2的两个同心圆,其中阴影部分为小圆内部一个90°的扇形,向大圆上投掷飞镖,则镖针落在阴影部分的概率为 ( )
9.[2022·济南]如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
10.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
11.如图,现有一个转盘被平均分成6等份,分别标有数字2,3,4,5,6,7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)转到数字10是 ;(从“不确定事件”“必然事件”“不可能事件”选一个填入)
(2)转动转盘,转出的数字大于3的概率是 ;
(3)现有两张分别写有3和4的卡片,若随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度,求这三条线段能构成三角形的概率是多少
12.丽丽和小明两位同学一起玩飞镖游戏,飞镖的靶子设计如图所示,已知从里到外的三个圆的半径分别为1,2,4,圆形靶子被分为A,B,C三个区域.如果飞镖投出后没有落在靶子上,或是停留在圆周上,那么可以重新投镖.
(1)分别求出飞镖落在三个区域的概率;
(2)丽丽和小明约定,如果飞镖停落在A,B 区域,则丽丽得三分,如果飞镖落在C区域,则小明得一分,你认为这个游戏公平吗 说明理由.如果不公平,请你修改得分规则,使这个游戏公平.
参考答案
夯基础
1.A 2.B 3.D 4.B 5.D 6.C 7.D
12.④
13.解:(1)2种;
练能力
1.A 2.C 3.A 4.B 5.D 6.D 7.A
8.B
11.解:(1)转到数字10是不可能事件,故答案为:不可能事件;
(2)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
∴转出的数字大于3的概率是 故答案为:
(3)∵4-3<第三边的长<4+3,即1<第三边的长<7,
∴与3和4能组成三角形的有2,3,4,5,6,
∵转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能构成三角形的结果有5种,
∴这三条线段能构成三角形的概率是
12.解:(1)∵三个圆的半径分别为1,2,4,
∴飞镖落在A区域的概率是 飞镖落在B区域的概率是 飞镖落在C区域的概率是
∵P(丽丽得分)=P(小明得分),
∴这个游戏公平.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 概率初步
3 等可能事件的概率
面积类游戏 第4课时 转盘类游戏
夸基础
1.如图所示的是由8个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是( )
D.1
2.如图,在平行四边形纸片上做随机扎针实验,针头扎在阴影区域内的概率为( )
3.如图,四个转盘分别被分成不同的等份,若让转盘自由转动一次,停止后指针落在阴影区域内的概率最大的转盘是 ( )
4.如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,事件“指针所落扇形中的数大于3”的概率为 ( )
5.如图是一个被分成6等份的转盘,小明转动了2次,结果指针都停留在红色区域,小明第3次转动指针停留在红色区域的概率为( )
A.1 B.0
6.小明将如图的转盘分成n(n是正整数)个扇形,并使得各个扇形的面积都相等,然后他在这些扇形区域内分别标连接偶数数字2,4.6, ,2n(每个区域内标注1个数字,且各区域内标注的数字互不相同),转动转盘1次,当转盘停止转动时,若事件“指针所落区域标注的数字大于8”的概率是,则n的取值为( )
A.36 B.30 C.24 D.1 8
7.如图是一个可以自由转动的转盘,转动转盘,转盘停止后,指针落在C区域的概率是( )
8.如图,一块飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖(每次飞镖均落在纸板上),击中阴影区域的概率是 .
9.如图,在4×4的正方形网格中,有4个小正方形已经涂黑,若再涂黑任意1个白色的小正方形(每个白色小正方形被涂黑的可能性相同),使新构成的黑色部分图形是轴对称图形的概率是 .
10.如图,一个质地均匀的正五边形转盘,指针的位置固定,当转盘自由转动停止后,观察指针指向区域内的数(若指针正好指向分界线,则重新转一次),这个数是一个奇数的概率是 .
11.如图所示,甲、乙两个带指针的转盘分别被分成三个面积相等的扇形(两个转盘除表面数字不同外,其他完全相同),转盘甲上的数字分别是-6,-1,8,转盘乙上的数字分别是-4,5,7.那么,转动转盘,转盘甲指针指向正数的概率是 ;转盘乙指针指向正数的概率是 .(规定:指针恰好停留在分界线上,则重新转一次)
12.如图所示的转盘,被分成面积相等的6个扇形,分别标注数字1,2,3,4,5,6,随机转动转盘一次,当转盘停止转动时,则下列事件:①指针落在区域内的数字是奇数;②指针落在区域内的数字是3的倍数;③指针落在区域内的数字是偶数;④指针落在区域内的数字比5小,其中发生的可能性最大的事件是 .(填序号)
13.如图是一个飞镖盘,(1)任意打一个飞镖到镖盘上有几种不同的结果 (2)求出打中“□”的概率.
练能力
1.如图,任意将图中的某一白色方块涂黑后,能使所有黑色方块构成的图形是轴对称图形的概率是( )
2.用力旋转如图所示的转盘甲和转盘乙,如果想让指针停在阴影部分.选取哪个转盘成功的机会比较大( )
A.转盘甲 B.转盘乙 C.两个一样大 D.无法确定
3.如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是 ( )
4.如图,正方形ABCD及其内切圆O,随机地往正方形内投一粒米,落在阴影部分的概率是( )
5.以下转盘分别被分成2个,4个,5个,6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在阴影区域的概率是则对应的转盘是( )
6[2021·安徽]如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是( )
7.分别向如图所示的四个区域投掷一个小球,小球落在阴影部分的概率最小的是( )
8.如图所示,镖盘为两个半径为1:2的两个同心圆,其中阴影部分为小圆内部一个90°的扇形,向大圆上投掷飞镖,则镖针落在阴影部分的概率为 ( )
9.[2022·济南]如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
10.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
11.如图,现有一个转盘被平均分成6等份,分别标有数字2,3,4,5,6,7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)转到数字10是 ;(从“不确定事件”“必然事件”“不可能事件”选一个填入)
(2)转动转盘,转出的数字大于3的概率是 ;
(3)现有两张分别写有3和4的卡片,若随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度,求这三条线段能构成三角形的概率是多少
12.丽丽和小明两位同学一起玩飞镖游戏,飞镖的靶子设计如图所示,已知从里到外的三个圆的半径分别为1,2,4,圆形靶子被分为A,B,C三个区域.如果飞镖投出后没有落在靶子上,或是停留在圆周上,那么可以重新投镖.
(1)分别求出飞镖落在三个区域的概率;
(2)丽丽和小明约定,如果飞镖停落在A,B 区域,则丽丽得三分,如果飞镖落在C区域,则小明得一分,你认为这个游戏公平吗 说明理由.如果不公平,请你修改得分规则,使这个游戏公平.
参考答案
夯基础
1.A 2.B 3.D 4.B 5.D 6.C 7.D
12.④
13.解:(1)2种;
练能力
1.A 2.C 3.A 4.B 5.D 6.D 7.A
8.B
11.解:(1)转到数字10是不可能事件,故答案为:不可能事件;
(2)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,
∴转出的数字大于3的概率是 故答案为:
(3)∵4-3<第三边的长<4+3,即1<第三边的长<7,
∴与3和4能组成三角形的有2,3,4,5,6,
∵转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能构成三角形的结果有5种,
∴这三条线段能构成三角形的概率是
12.解:(1)∵三个圆的半径分别为1,2,4,
∴飞镖落在A区域的概率是 飞镖落在B区域的概率是 飞镖落在C区域的概率是
∵P(丽丽得分)=P(小明得分),
∴这个游戏公平.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
