鲁教版七年级下册期中检测数学试题(含答案)
文档属性
| 名称 | 鲁教版七年级下册期中检测数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 17:44:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
七年级下册数学期中检测题
时间:90分钟 满分:120分 得分:
一、选择题(每题3分,共30分)
1.在铺设铁轨时,两条直轨必须是互相平行的,如图,已知∠2是直角,那么再度量图中已标出的哪个角,不能判断两条直轨是否平行( )
A.∠1 B.∠3 C.∠4 D.∠5
2.下列事件中,是随机事件的是 ( )
A.通常加热到100℃时,水沸腾 B.随意翻到一本书的某页,这页的页码是偶数
C.任意画一个三角形,其内角和是360° D.明天太阳从东方升起
3.利用加减消元法解方程组 下列做法正确的是( )
A.要消去y,可以将①×5+②×2 B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3 D.要消去x,可以将①×(-5)+②×2
4.某抗战纪念馆馆长找到大学生团干部小张,联系青年志愿者在周日参加活动,活动累计56个小时的工作时间,需要每名男生工作5个小时,每名女生工作4个小时,小张可以安排学生参加活动的方案共有 ( )
A.1种 B.2种 C.3种 D.4种
5.下列四个命题中,真命题是 ( )
A.“任意四边形内角和为360°”是不可能事件
B.二元一次方程3x+2y=14的一组整数解是x=2,y=4
C.“预计本题的正确率是95%”表示100位考生中一定有95人做对
D.频率就是概率
6.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,若一次摸出1个,则取出的小球标号小于4的概率是( )
D.1
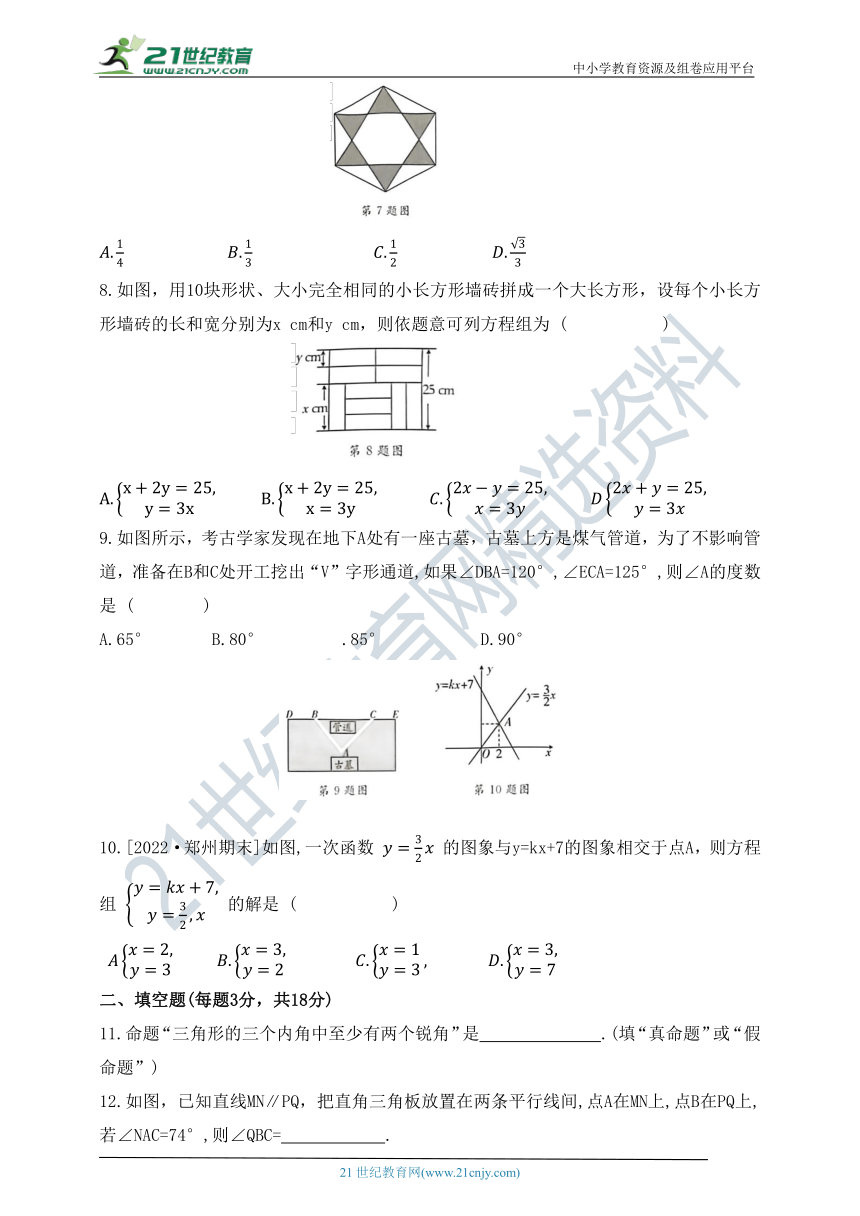
7.将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为 ( )
8.如图,用10块形状、大小完全相同的小长方形墙砖拼成一个大长方形,设每个小长方形墙砖的长和宽分别为x cm和y cm,则依题意可列方程组为 ( )
9.如图所示,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B和C处开工挖出“V”字形通道,如果∠DBA=120°,∠ECA=125°,则∠A的度数是 ( )
A.65° B.80° .85° D.90°
10.[2022·郑州期末]如图,一次函数 的图象与y=kx+7的图象相交于点A,则方程组 的解是 ( )
二、填空题(每题3分,共18分)
11.命题“三角形的三个内角中至少有两个锐角”是 .(填“真命题”或“假命题”)
12.如图,已知直线MN∥PQ,把直角三角板放置在两条平行线间,点A在MN上,点B在PQ上,若∠NAC=74°,则∠QBC= .
13.在关于x,y的二元一次方程组 中,若2x+3y-2=0,则a的值为 .
14.在一个不透明的袋子中装有除颜色外其余均相同的9个小球,其中红球4个,黑球5个.若再放入m个一样的黑球并摇匀,此时,随机摸出一个球是黑球的概率等于 则m的值为 .
15.如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,估计下列事件发生的可能性的大小:①指针落在标有3的倍数区域内;②指针落在标有5的区域内;③指针落在标有偶数的区域内.并将这些事件的序号按发生的可能性从小到大的顺序排成一列是 .(填序号)
16.三个同学对问题“若方程组的解是 求方程组 的解”提出各自的想法.甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
三、解答题(共72分)
17.(6分)解方程组:
18.(8分)“五·一”期间,某书城为了吸引读者,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元的书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色,黄色,绿色区域,那么读者就可以分别获得45元,30元,25元的购书券,凭购书券可以在书城继续购书.如果读者不愿意转转盘,那么可以直接获得10元的购书券.
(1)写出转动一次转盘获得45元购书券的概率;
(2)转转盘和直接获得购书券,你认为哪种方式对读者更合算 请说明理由.
19.(8分)如图,已知EF∥AD,∠1=∠2,∠BAC=80°.
(1)求证:DG∥AB;
(2)求∠AGD的度数.
20.(8分)为支援抗疫前线,某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为每吨3万元,乙物资单价为每吨2万元,采购两种物资共花费1380万元,求甲、乙两种物资各采购了多少吨
21.(8分)如图是小明和小颖共同设计的可自由转动的转盘,转盘被等分成10份,上面写有10个有理数.转动转盘,当转盘停止转动时,
(1)求指针指向正数的概率;
(2)若指针指向绝对值小于6的数,则小明胜,指针指向其他数,则小颖胜,这个游戏对双方公平吗 请说明理由.
22.(10分)如图,已知∠2=∠ABD,∠A+∠1=180° .
(1)判断AF与BE的位置关系,并说明理由;
(2)若BE平分∠ABD,DF⊥AF于点F,∠ABD=50°,求∠DEC的度数.
23.(12分)[2022·麻栗坡县期末]如图,直线l 的函数解析式为y=2x-2,直线l 与x轴交于点D,直线l :y=kx+b与x轴交于点A,且经过点B,如图所示,直线l ,l 交于点C(m,2).
(1)求点C,点D的坐标;
(2)求直线l 的函数解析式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组 的解.
24.(12分)(1)在图1中,请直接写出∠A,∠B,∠C,∠D之间的数量关系;
(2)如果图2中,∠D=40°,∠B=36°,AP与CP分别是∠DAB和∠DCB的角平分线,试求∠P的度数;
(3)如果图2中∠D和∠B为任意角,其他条件不变,试问∠P与∠D,∠B之间存在着怎样的数量关系(直接写出结论即可).
参考答案
1.A 2.B 3.D 4.C 5.B 6.C 7.B 8.B 9.A 10.A
11.真命题 12.16° 13.3 14.11 15.②①③
17.解:整理方程组,得
①×2-②,得-7y=-7,解得y=1,
把y=1代入①,得x-2=3,解得x=5,
∴方程组得解为
18.解:(1)P(获得45元购书券)
(2)转转盘对读者更合算。
理由: 元).
∵15元>10元,∴转转盘对读者更合算。
19.解:(1)证明:∵EF∥AD.∴∠2=∠3.
∵∠1=∠2,∴∠1=∠3.∴AB∥DG.
(2)∵AB∥DG,∴∠BAC+∠AGD=180°.
∵∠BAC=80°,∴∠AGD=100°.
20.解:设甲种物资采购了x吨,乙种物资采购了y吨.
依题意,得 解得
答:甲种物资采购了300吨,乙种物资采购了240吨.
21.解:(1)P(指针指向正数)
答:指针指向正数的概率为
(2)解:这个游戏对双方不公平,理由如下:
因为P(指针指向绝对值小于6的数P(指针指向其他数)
因为 所以这个游戏对双方不公平.
22.解:(1)AF∥BE.理由如下:
∵∠2=∠ABD.∴AB∥CE,∴∠1=∠ABE.
∵∠A+∠1=180°,∴∠A+∠ABE=180°,∴AF∥BE;
(2)∵DF⊥AF,AF∥BE.∴DF ⊥BE,∴∠BED=90°.
∵∠ABD=50°,BE平分∠ABD,∴∴∠D=65°.
∵AB∥CE,∴∠2=∠ABD=50°,∴∠DEC=180°-50°-65°=65°.
23.解:(1)∵直线l ,l 交于点(m,2),
∴把C(m,2)坐标代入y=2x-2中,得2=2m-2,∴m=2,则C(2,2),
又∵直线l 与x轴交于D点,故2x-2=0,∴x=1,则D(1,0).
(2)把点B(3,1),C(2,2)代入直线
得 解得
∴直线l 的解析式为:y=-x+4.
(3)把y=0代入y=-x+4中,得-x+4=0,x=4,∴A(4,0).
又∵D(1,0),C(2,2),∴AD=4-1=3,
(4)由图象知,点C的坐标即方程组 的解,
24.解:(1)∠A+∠D=∠C+∠B;
∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,且∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
(2)由(1)可得∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠PAB+∠P.②
∵∠DAB和∠DCB的角平分线AP与CP 相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②,得∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,∴∠D+∠B=2∠P,
又∵∠D=40°,∠B=36°,∴40°+36°=2∠P,∴∠P=38°;
(3)存在的数量关系为:∠D+∠B=2∠P.
由(1)可得∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠DCB的角平分线AP与CP 相交于点P,∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②,得∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,∴∠D+∠B=2∠P.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
七年级下册数学期中检测题
时间:90分钟 满分:120分 得分:
一、选择题(每题3分,共30分)
1.在铺设铁轨时,两条直轨必须是互相平行的,如图,已知∠2是直角,那么再度量图中已标出的哪个角,不能判断两条直轨是否平行( )
A.∠1 B.∠3 C.∠4 D.∠5
2.下列事件中,是随机事件的是 ( )
A.通常加热到100℃时,水沸腾 B.随意翻到一本书的某页,这页的页码是偶数
C.任意画一个三角形,其内角和是360° D.明天太阳从东方升起
3.利用加减消元法解方程组 下列做法正确的是( )
A.要消去y,可以将①×5+②×2 B.要消去x,可以将①×3+②×(-5)
C.要消去y,可以将①×5+②×3 D.要消去x,可以将①×(-5)+②×2
4.某抗战纪念馆馆长找到大学生团干部小张,联系青年志愿者在周日参加活动,活动累计56个小时的工作时间,需要每名男生工作5个小时,每名女生工作4个小时,小张可以安排学生参加活动的方案共有 ( )
A.1种 B.2种 C.3种 D.4种
5.下列四个命题中,真命题是 ( )
A.“任意四边形内角和为360°”是不可能事件
B.二元一次方程3x+2y=14的一组整数解是x=2,y=4
C.“预计本题的正确率是95%”表示100位考生中一定有95人做对
D.频率就是概率
6.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4,若一次摸出1个,则取出的小球标号小于4的概率是( )
D.1
7.将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为 ( )
8.如图,用10块形状、大小完全相同的小长方形墙砖拼成一个大长方形,设每个小长方形墙砖的长和宽分别为x cm和y cm,则依题意可列方程组为 ( )
9.如图所示,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B和C处开工挖出“V”字形通道,如果∠DBA=120°,∠ECA=125°,则∠A的度数是 ( )
A.65° B.80° .85° D.90°
10.[2022·郑州期末]如图,一次函数 的图象与y=kx+7的图象相交于点A,则方程组 的解是 ( )
二、填空题(每题3分,共18分)
11.命题“三角形的三个内角中至少有两个锐角”是 .(填“真命题”或“假命题”)
12.如图,已知直线MN∥PQ,把直角三角板放置在两条平行线间,点A在MN上,点B在PQ上,若∠NAC=74°,则∠QBC= .
13.在关于x,y的二元一次方程组 中,若2x+3y-2=0,则a的值为 .
14.在一个不透明的袋子中装有除颜色外其余均相同的9个小球,其中红球4个,黑球5个.若再放入m个一样的黑球并摇匀,此时,随机摸出一个球是黑球的概率等于 则m的值为 .
15.如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,估计下列事件发生的可能性的大小:①指针落在标有3的倍数区域内;②指针落在标有5的区域内;③指针落在标有偶数的区域内.并将这些事件的序号按发生的可能性从小到大的顺序排成一列是 .(填序号)
16.三个同学对问题“若方程组的解是 求方程组 的解”提出各自的想法.甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
三、解答题(共72分)
17.(6分)解方程组:
18.(8分)“五·一”期间,某书城为了吸引读者,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元的书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色,黄色,绿色区域,那么读者就可以分别获得45元,30元,25元的购书券,凭购书券可以在书城继续购书.如果读者不愿意转转盘,那么可以直接获得10元的购书券.
(1)写出转动一次转盘获得45元购书券的概率;
(2)转转盘和直接获得购书券,你认为哪种方式对读者更合算 请说明理由.
19.(8分)如图,已知EF∥AD,∠1=∠2,∠BAC=80°.
(1)求证:DG∥AB;
(2)求∠AGD的度数.
20.(8分)为支援抗疫前线,某省红十字会采购甲、乙两种抗疫物资共540吨,甲物资单价为每吨3万元,乙物资单价为每吨2万元,采购两种物资共花费1380万元,求甲、乙两种物资各采购了多少吨
21.(8分)如图是小明和小颖共同设计的可自由转动的转盘,转盘被等分成10份,上面写有10个有理数.转动转盘,当转盘停止转动时,
(1)求指针指向正数的概率;
(2)若指针指向绝对值小于6的数,则小明胜,指针指向其他数,则小颖胜,这个游戏对双方公平吗 请说明理由.
22.(10分)如图,已知∠2=∠ABD,∠A+∠1=180° .
(1)判断AF与BE的位置关系,并说明理由;
(2)若BE平分∠ABD,DF⊥AF于点F,∠ABD=50°,求∠DEC的度数.
23.(12分)[2022·麻栗坡县期末]如图,直线l 的函数解析式为y=2x-2,直线l 与x轴交于点D,直线l :y=kx+b与x轴交于点A,且经过点B,如图所示,直线l ,l 交于点C(m,2).
(1)求点C,点D的坐标;
(2)求直线l 的函数解析式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组 的解.
24.(12分)(1)在图1中,请直接写出∠A,∠B,∠C,∠D之间的数量关系;
(2)如果图2中,∠D=40°,∠B=36°,AP与CP分别是∠DAB和∠DCB的角平分线,试求∠P的度数;
(3)如果图2中∠D和∠B为任意角,其他条件不变,试问∠P与∠D,∠B之间存在着怎样的数量关系(直接写出结论即可).
参考答案
1.A 2.B 3.D 4.C 5.B 6.C 7.B 8.B 9.A 10.A
11.真命题 12.16° 13.3 14.11 15.②①③
17.解:整理方程组,得
①×2-②,得-7y=-7,解得y=1,
把y=1代入①,得x-2=3,解得x=5,
∴方程组得解为
18.解:(1)P(获得45元购书券)
(2)转转盘对读者更合算。
理由: 元).
∵15元>10元,∴转转盘对读者更合算。
19.解:(1)证明:∵EF∥AD.∴∠2=∠3.
∵∠1=∠2,∴∠1=∠3.∴AB∥DG.
(2)∵AB∥DG,∴∠BAC+∠AGD=180°.
∵∠BAC=80°,∴∠AGD=100°.
20.解:设甲种物资采购了x吨,乙种物资采购了y吨.
依题意,得 解得
答:甲种物资采购了300吨,乙种物资采购了240吨.
21.解:(1)P(指针指向正数)
答:指针指向正数的概率为
(2)解:这个游戏对双方不公平,理由如下:
因为P(指针指向绝对值小于6的数P(指针指向其他数)
因为 所以这个游戏对双方不公平.
22.解:(1)AF∥BE.理由如下:
∵∠2=∠ABD.∴AB∥CE,∴∠1=∠ABE.
∵∠A+∠1=180°,∴∠A+∠ABE=180°,∴AF∥BE;
(2)∵DF⊥AF,AF∥BE.∴DF ⊥BE,∴∠BED=90°.
∵∠ABD=50°,BE平分∠ABD,∴∴∠D=65°.
∵AB∥CE,∴∠2=∠ABD=50°,∴∠DEC=180°-50°-65°=65°.
23.解:(1)∵直线l ,l 交于点(m,2),
∴把C(m,2)坐标代入y=2x-2中,得2=2m-2,∴m=2,则C(2,2),
又∵直线l 与x轴交于D点,故2x-2=0,∴x=1,则D(1,0).
(2)把点B(3,1),C(2,2)代入直线
得 解得
∴直线l 的解析式为:y=-x+4.
(3)把y=0代入y=-x+4中,得-x+4=0,x=4,∴A(4,0).
又∵D(1,0),C(2,2),∴AD=4-1=3,
(4)由图象知,点C的坐标即方程组 的解,
24.解:(1)∠A+∠D=∠C+∠B;
∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,且∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
(2)由(1)可得∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠PAB+∠P.②
∵∠DAB和∠DCB的角平分线AP与CP 相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②,得∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,∴∠D+∠B=2∠P,
又∵∠D=40°,∠B=36°,∴40°+36°=2∠P,∴∠P=38°;
(3)存在的数量关系为:∠D+∠B=2∠P.
由(1)可得∠DAP+∠D=∠P+∠DCP,①∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠DCB的角平分线AP与CP 相交于点P,∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②,得∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,∴∠D+∠B=2∠P.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
