【班海精品】冀教版(新)六下-第六单元 1.3数与代数-式与方程【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)六下-第六单元 1.3数与代数-式与方程【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-12 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
式与方程
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
01
新课精讲
02
学以致用
03
课堂小结
04
课前导入
情景导入
怎样用字母表示数、数量关系、运算律和计算公式?
方程与等式有什么区别和联系?你能举例说明等式的性质吗?
用方程解决实际问题,有什么特点?
新课精讲
探索新知
怎样用字母表示数、数量关系、运算律和计算公式?
1. 用字母表示数:如x=7,a=6,m=0。
2. 用字母表示数量关系:
如果用s表示路程,用v表示速度,用t表示时间,那么路程、速度、时间之间的关系可以表示为( )。
s= v t
探究点1 解用字母表示数、运算定律、计算公式、数量关系等
探索新知
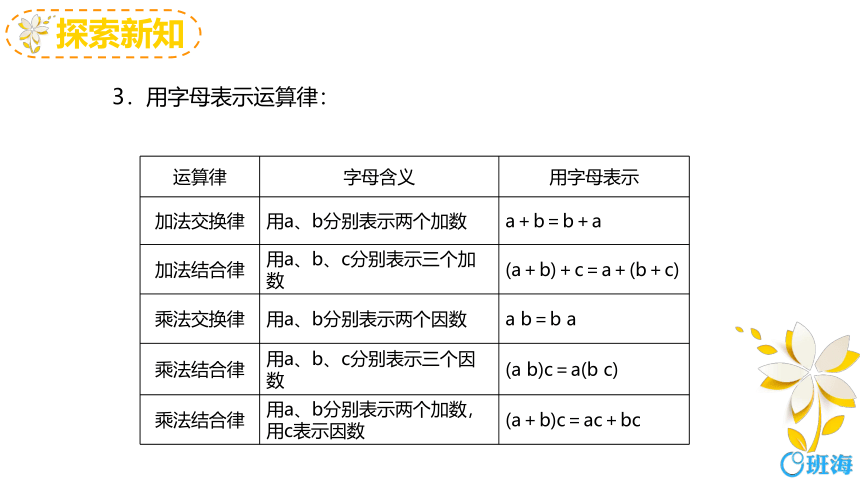
运算律 字母含义 用字母表示
加法交换律 用a、b分别表示两个加数 a+b=b+a
加法结合律 用a、b、c分别表示三个加数 (a+b)+c=a+(b+c)
乘法交换律 用a、b分别表示两个因数 a b=b a
乘法结合律 用a、b、c分别表示三个因数 (a b)c=a(b c)
乘法结合律 用a、b分别表示两个加数,用c表示因数 (a+b)c=ac+bc
3.用字母表示运算律:
探索新知
4. 用字母表示公式:
长方形的周长:C=(a+b)×2
长方形的面积:S=ab
正方形的周长:C=4a
正方形的面积:S=a2
三角形的面积:S=ah÷2
平行四边形的面积:S=ah
梯形的面积:S=(a+b)h÷2
探索新知
方程与等式有什么区别和联系?你能举例说明等式的性质吗?
探究点2 方程与等式的联系与区别,等式的性质
要知道方程与等式的区别和联系,先要知道方程与等式的意义。
区别 联系
等式 等式的意义:表示( )关系的式子叫做等式。即用“=”连接起来的式子是等式
方程 方程的意义:含有( )的( )叫做方程。 特征:含有( )数,有等号
等式
方程
相等
未知数
等式
未知
探索新知
等式的性质 例子
例子等式的性质1:等式两边同时( )或( )同一个数,左右两边仍然相等 8+2=10 8+2+5=10+5 → 15=15
8+2-6=10-6 → 4=4
等式的性质2:等式两边同时( )同一个数或( )同一个不为0的数,左右两边仍然相等 a=20 a×5=20×5 → 5a=100
a÷2=20÷2 → a÷2=102
加上
减去
乘
除以
探索新知
你能对我们学过的简单应用题进行分类吗
不同点
方程的解 使( )左右两边相等的( )的值叫做方程的解。方程的解是一个( )
解方程 求方程的解的( )叫做解方程。解方程是一个过程
方程
未知数
数值
过程
探究点3 运用等式的性质解方程
探索新知
检验方程的解的方法:把未知数的( )代入原方程,看方程左右两边是否( )。如果左右两边相等,那么这个值就是方程的解。
值
相等
探索新知
用方程解决实际问题,有什么特点?
用方程解决实际问题:列方程解实际问题是指用字母代替实际问题中的未知量,根据数量间的相等关系列出方程,通过解方程来解答实际问题。
探究点4 列方程解应用题
探索新知
(1)列方程解实际问题的一般步骤:
① 找出( ),用字母x表示;
② 分析实际问题中的数量关系,找出( )关系,列方程;
③ 解方程并检验作答。
未知量
等量
(2)找等量关系是列方程解决实际问题的关键,找等量关系可以通过以下几种方法:
①从题目的关键句中找;②从常见的等量关系中找;
③根据图形的周长、面积和体积计算公式找等量关系,
④从题目的叙述顺序中找;
⑤借助线段图找。
探索新知
(3)用方程解实际问题与用算术法解实际问题的区别:
用方程解实际问题 用算术法解实际问题
未知量用字母x表示,参与列式; 根据题意找出数量之间的相等关系,列出含有未知数x的等式 未知量不参与列式;根据题目中已知数量和未知量之间的关系,确定解答步骤,然后列式计算
典题精讲
1.填空。
(1)一支中性笔的价格是m元,一支钢笔的价格比它的1.5倍还多n元,一支钢笔的价格是( )元。
(2)三角形的底是a cm,高是h cm,面积是( )cm2。
(3)用字母表示乘法分配律是( )。
(4)甲数比乙数的4倍多a,如果甲数是x,那么乙数是( );如果乙数是x,那么甲数是( )。
1.5m+n
ah
a(b+c)=ab+ac
(x-a)÷4
4x+a
典题精讲
2.判断。(对的画“√”,错的画“×”)
(1)含有未知数的式子叫方程。 ( )
(2)方程72-5x=47的解是x=5。 ( )
(3)m的2倍与n的差写成式子是2m-n,这个式子是方程。
( )
(4)方程一定是等式,等式不一定是方程。 ( )
(5)5x-8<7是方程。 ( )
×
√
×
√
×
典题精讲
3.解方程。
x+25%=10 4x-3×8=12
1.3x+2.4x=1.11 8(x-2)=2(x-7)
x=19.5
x=9
x=0.3
x=
易错提醒
下列的解方程对吗?若不对,请改正。
(1)9.8-x=7.2
解: x=7.2+9.8
x=17( )
改正:
×
x=9.8-7.2
x=2.6
(2) ÷x=
解: x = ×
x= ( )
改正:
×
x= ÷
x=
辨析:当未知数是方程中的减数或除数时,解方程出现错误。
学以致用
小试牛刀
1.四年级订阅《中国少年报》120份,比五年级多订阅x份,120-x表示什么?每份《中国少年报》a 元,120a表示什么?(120- x)a表示什么?
答:120-x表示五年级订阅《中国少年报》的份数;
120a表示四年级订阅的《中国少年报》的总价;
(120-x)a表示五年级订阅的《中国少年报》的总价。
小试牛刀
2.根据等式的性质在 里填运算符号,在 里填数。
x-35=60
x-35+35= 60
x=
0.9x=6.3
0.9x÷0.9=6.3
x=
+
35
95
÷
0.9
7
小试牛刀
3.列方程解决问题。
(1)某小学篮球队和足球队一共有105人,其中篮球队的人数是足球队的2.5倍。篮球队和足球队各有多少人?
解:设足球队有x人。
x+2.5x=105
x= 30
105-30= 75(人)
答:篮球队和足球队各有75、30人。
小试牛刀
3.列方程解决问题。
(2)甲、乙两地相距480 km,一辆客车和一辆货车同时分别从甲、乙两地相对开出,3.2小时相遇。客车每小时行85 km,货车每小时行多少千米?
解:设货车每小时行x km。
(85+x)×3.2=480
x=65
答:货车每小时行65千米。
课堂小结
归纳总结:
1.解用字母表示数、运算定律、计算公式、数量关系等;
2.方程与等式的联系与区别,等式的性质;
3.运用等式的性质解方程;
4.列方程解应用题。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
式与方程
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
01
新课精讲
02
学以致用
03
课堂小结
04
课前导入
情景导入
怎样用字母表示数、数量关系、运算律和计算公式?
方程与等式有什么区别和联系?你能举例说明等式的性质吗?
用方程解决实际问题,有什么特点?
新课精讲
探索新知
怎样用字母表示数、数量关系、运算律和计算公式?
1. 用字母表示数:如x=7,a=6,m=0。
2. 用字母表示数量关系:
如果用s表示路程,用v表示速度,用t表示时间,那么路程、速度、时间之间的关系可以表示为( )。
s= v t
探究点1 解用字母表示数、运算定律、计算公式、数量关系等
探索新知
运算律 字母含义 用字母表示
加法交换律 用a、b分别表示两个加数 a+b=b+a
加法结合律 用a、b、c分别表示三个加数 (a+b)+c=a+(b+c)
乘法交换律 用a、b分别表示两个因数 a b=b a
乘法结合律 用a、b、c分别表示三个因数 (a b)c=a(b c)
乘法结合律 用a、b分别表示两个加数,用c表示因数 (a+b)c=ac+bc
3.用字母表示运算律:
探索新知
4. 用字母表示公式:
长方形的周长:C=(a+b)×2
长方形的面积:S=ab
正方形的周长:C=4a
正方形的面积:S=a2
三角形的面积:S=ah÷2
平行四边形的面积:S=ah
梯形的面积:S=(a+b)h÷2
探索新知
方程与等式有什么区别和联系?你能举例说明等式的性质吗?
探究点2 方程与等式的联系与区别,等式的性质
要知道方程与等式的区别和联系,先要知道方程与等式的意义。
区别 联系
等式 等式的意义:表示( )关系的式子叫做等式。即用“=”连接起来的式子是等式
方程 方程的意义:含有( )的( )叫做方程。 特征:含有( )数,有等号
等式
方程
相等
未知数
等式
未知
探索新知
等式的性质 例子
例子等式的性质1:等式两边同时( )或( )同一个数,左右两边仍然相等 8+2=10 8+2+5=10+5 → 15=15
8+2-6=10-6 → 4=4
等式的性质2:等式两边同时( )同一个数或( )同一个不为0的数,左右两边仍然相等 a=20 a×5=20×5 → 5a=100
a÷2=20÷2 → a÷2=102
加上
减去
乘
除以
探索新知
你能对我们学过的简单应用题进行分类吗
不同点
方程的解 使( )左右两边相等的( )的值叫做方程的解。方程的解是一个( )
解方程 求方程的解的( )叫做解方程。解方程是一个过程
方程
未知数
数值
过程
探究点3 运用等式的性质解方程
探索新知
检验方程的解的方法:把未知数的( )代入原方程,看方程左右两边是否( )。如果左右两边相等,那么这个值就是方程的解。
值
相等
探索新知
用方程解决实际问题,有什么特点?
用方程解决实际问题:列方程解实际问题是指用字母代替实际问题中的未知量,根据数量间的相等关系列出方程,通过解方程来解答实际问题。
探究点4 列方程解应用题
探索新知
(1)列方程解实际问题的一般步骤:
① 找出( ),用字母x表示;
② 分析实际问题中的数量关系,找出( )关系,列方程;
③ 解方程并检验作答。
未知量
等量
(2)找等量关系是列方程解决实际问题的关键,找等量关系可以通过以下几种方法:
①从题目的关键句中找;②从常见的等量关系中找;
③根据图形的周长、面积和体积计算公式找等量关系,
④从题目的叙述顺序中找;
⑤借助线段图找。
探索新知
(3)用方程解实际问题与用算术法解实际问题的区别:
用方程解实际问题 用算术法解实际问题
未知量用字母x表示,参与列式; 根据题意找出数量之间的相等关系,列出含有未知数x的等式 未知量不参与列式;根据题目中已知数量和未知量之间的关系,确定解答步骤,然后列式计算
典题精讲
1.填空。
(1)一支中性笔的价格是m元,一支钢笔的价格比它的1.5倍还多n元,一支钢笔的价格是( )元。
(2)三角形的底是a cm,高是h cm,面积是( )cm2。
(3)用字母表示乘法分配律是( )。
(4)甲数比乙数的4倍多a,如果甲数是x,那么乙数是( );如果乙数是x,那么甲数是( )。
1.5m+n
ah
a(b+c)=ab+ac
(x-a)÷4
4x+a
典题精讲
2.判断。(对的画“√”,错的画“×”)
(1)含有未知数的式子叫方程。 ( )
(2)方程72-5x=47的解是x=5。 ( )
(3)m的2倍与n的差写成式子是2m-n,这个式子是方程。
( )
(4)方程一定是等式,等式不一定是方程。 ( )
(5)5x-8<7是方程。 ( )
×
√
×
√
×
典题精讲
3.解方程。
x+25%=10 4x-3×8=12
1.3x+2.4x=1.11 8(x-2)=2(x-7)
x=19.5
x=9
x=0.3
x=
易错提醒
下列的解方程对吗?若不对,请改正。
(1)9.8-x=7.2
解: x=7.2+9.8
x=17( )
改正:
×
x=9.8-7.2
x=2.6
(2) ÷x=
解: x = ×
x= ( )
改正:
×
x= ÷
x=
辨析:当未知数是方程中的减数或除数时,解方程出现错误。
学以致用
小试牛刀
1.四年级订阅《中国少年报》120份,比五年级多订阅x份,120-x表示什么?每份《中国少年报》a 元,120a表示什么?(120- x)a表示什么?
答:120-x表示五年级订阅《中国少年报》的份数;
120a表示四年级订阅的《中国少年报》的总价;
(120-x)a表示五年级订阅的《中国少年报》的总价。
小试牛刀
2.根据等式的性质在 里填运算符号,在 里填数。
x-35=60
x-35+35= 60
x=
0.9x=6.3
0.9x÷0.9=6.3
x=
+
35
95
÷
0.9
7
小试牛刀
3.列方程解决问题。
(1)某小学篮球队和足球队一共有105人,其中篮球队的人数是足球队的2.5倍。篮球队和足球队各有多少人?
解:设足球队有x人。
x+2.5x=105
x= 30
105-30= 75(人)
答:篮球队和足球队各有75、30人。
小试牛刀
3.列方程解决问题。
(2)甲、乙两地相距480 km,一辆客车和一辆货车同时分别从甲、乙两地相对开出,3.2小时相遇。客车每小时行85 km,货车每小时行多少千米?
解:设货车每小时行x km。
(85+x)×3.2=480
x=65
答:货车每小时行65千米。
课堂小结
归纳总结:
1.解用字母表示数、运算定律、计算公式、数量关系等;
2.方程与等式的联系与区别,等式的性质;
3.运用等式的性质解方程;
4.列方程解应用题。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
