【班海精品】冀教版(新)六下-第三单元 1.1正比例【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)六下-第三单元 1.1正比例【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
正比例
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
1
课前导入
2
新课精讲
3
学以致用
4
课堂小结
01
课前导入
情景导入
已知路程和时间,怎样求速度?
速度 = 路程÷时间
已知总价和数量,怎样求单价?
单价 = 总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
02
新课精讲
探索新知
下面是一辆汽车8:00出发时和行驶1小时候里程表上显示的千米数。
1
探究点 正比例的意义
(1)汽车1小时行驶了多少千米?
8814-8724=90(千米)
探索新知
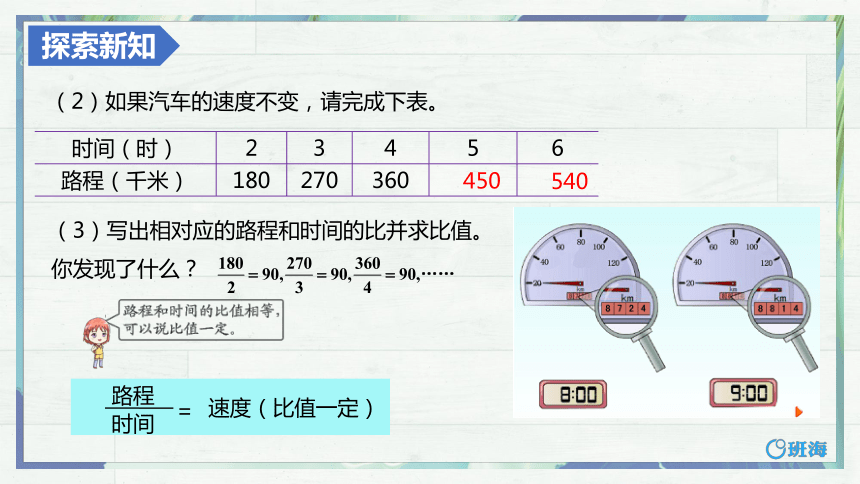
(2)如果汽车的速度不变,请完成下表。
时间(时) 2 3 4 5 6
路程(千米) 180 270 360
450
540
(3)写出相对应的路程和时间的比并求比值。
你发现了什么?
路程
时间
=
速度(比值一定)
探索新知
在速度一定的情况下,路程和时间有什么关系?
在上面的问题中,路程和时间是两种相关联的量,路程随着时间的变化而变化,而且,路程和时间的比值一定(速度一定)。我们说路程和时间这两种量成正比例。
探索新知
自动笔的单价为1.6元,请完成下表。
2
从上表中你发现了什么规律?
数量(支) 2 3 4 5 6 7 8
总价(元) 3.2 4.8 6.4
8
9.6
11.2
12.8
总价
数量
=单价(一定)
探索新知
花的钱数和买自动笔的数量这两种量成正比例吗?为什么?
像上面这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
探索新知
判断下面各题中的两种量是否成正比例,并说明理由。
1.飞机飞行的速度不变,飞行的路程和时间。
2.每千克苹果的价钱一定,付出的钱数和购买的苹果的数量。
3.每月收入一定,每月支出的钱数和剩下的钱数。
(1)题中,因为 =飞行速度(一定),所以飞行的路程和时间成正比例。
(2)题中,因为 =每千克苹果的价钱(一定),所以付出的钱数和购买苹果的数量成正比例。
(3)题中,因为每月支出的钱数+剩下的钱数=每月收入(一定),不符合正比例的规律,所以每月支出的钱数和剩下的钱数不成正比例。
飞行的路程
数量
付出的钱数
购买苹果的数量
探索新知
生活中成正比例的例子还有很多,如学校食堂每天的用煤量一定,用煤的总量和用的天数;小麦每公顷的产量一定,总产量和公顷数……
探索新知
一个化肥厂的生产情况如下表,根据表中数据回答问题。
(1)表中有哪两种相关联的量?
(2)表中相关联的两种量成正比例吗?为什么
时间和生产量是两种相关联的量。
成正比例,因为生产量随着时间的增多(减少)而增多(减少),且生产量÷时间=生产效率(一定),所以时间和生产量成正比例。
时间(天) 1 2 3 4 5 6 7
生产量(吨) 80 160 240 320 400 480 560
易错提醒
判断:圆的半径越大,它的面积就越大,所以圆的半径和面积成正比例。( )
辨析:没有正确理解正比例关系引起的判断错误。
×
03
学以致用
小试牛刀
1.填空。
(1)为提高自身的阅读能力,学生们积极订阅书刊,认真阅读。某书店销售《小学生天地》的份数和总价如下表:
①表中( )和( )是相关联的量,( )增加,( )也随着增加。
②总价与份数这两种相关联的量中相对应的两个数的比值都是( ),这个比值实际上是( )。
③因为总价与份数的比值一定,所以表中的两种量叫做成( )的量。
份数/份 1 2 3 4 5 6 …
总价/元 30 60 90 120 150 180 …
份数
总价
份数
总价
30
每份《小学生天地》的单价
正比例
小试牛刀
1.填空。
(2)路程与时间的比值是( ),当这个比值一定时,( )和( )成( )比例关系。
速度
路程
时间
正
2.判断。(对的画“√”,错的画“×”)
(1)长方形的长一定,宽和面积成正比例关系。 ( )
(2)正方形的面积与边长成正比例关系。 ( )
(3)比的前项一定,比的后项和比值成正比例关系。( )
(4)x÷y=4,x和y成正比例关系。 ( )
√
×
×
√
小试牛刀
3.选择。(将正确答案的字母填在括号里)
(1)下列各组中两种量不成正比例关系的是( )。
A.人的身高与年龄
B.y=5x中y和x
C.工作效率一定,工作总量和工作时间
D.圆的周长与直径
(2)甲数的 与乙数的 相等(甲、乙两数均不为0),
甲数与乙数( )。 A.成正比例关系
B.不成正比例关系
C.不成比例
D.无法判断
A
A
小试牛刀
3.选择。(将正确答案的字母填在括号里)
(3)下列各式中,x和y成正比例的是( )。
A.x+y=6 B.x=6y
C.x× y=1 D.x+1=6y
B
04
课堂小结
圆的半径和面积不成正比例,但是圆的半径的平方和面积成正比例。两种量是否成正比例,要根据正比例的意义去判断。
归纳总结:
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
正比例
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
1
课前导入
2
新课精讲
3
学以致用
4
课堂小结
01
课前导入
情景导入
已知路程和时间,怎样求速度?
速度 = 路程÷时间
已知总价和数量,怎样求单价?
单价 = 总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
02
新课精讲
探索新知
下面是一辆汽车8:00出发时和行驶1小时候里程表上显示的千米数。
1
探究点 正比例的意义
(1)汽车1小时行驶了多少千米?
8814-8724=90(千米)
探索新知
(2)如果汽车的速度不变,请完成下表。
时间(时) 2 3 4 5 6
路程(千米) 180 270 360
450
540
(3)写出相对应的路程和时间的比并求比值。
你发现了什么?
路程
时间
=
速度(比值一定)
探索新知
在速度一定的情况下,路程和时间有什么关系?
在上面的问题中,路程和时间是两种相关联的量,路程随着时间的变化而变化,而且,路程和时间的比值一定(速度一定)。我们说路程和时间这两种量成正比例。
探索新知
自动笔的单价为1.6元,请完成下表。
2
从上表中你发现了什么规律?
数量(支) 2 3 4 5 6 7 8
总价(元) 3.2 4.8 6.4
8
9.6
11.2
12.8
总价
数量
=单价(一定)
探索新知
花的钱数和买自动笔的数量这两种量成正比例吗?为什么?
像上面这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
探索新知
判断下面各题中的两种量是否成正比例,并说明理由。
1.飞机飞行的速度不变,飞行的路程和时间。
2.每千克苹果的价钱一定,付出的钱数和购买的苹果的数量。
3.每月收入一定,每月支出的钱数和剩下的钱数。
(1)题中,因为 =飞行速度(一定),所以飞行的路程和时间成正比例。
(2)题中,因为 =每千克苹果的价钱(一定),所以付出的钱数和购买苹果的数量成正比例。
(3)题中,因为每月支出的钱数+剩下的钱数=每月收入(一定),不符合正比例的规律,所以每月支出的钱数和剩下的钱数不成正比例。
飞行的路程
数量
付出的钱数
购买苹果的数量
探索新知
生活中成正比例的例子还有很多,如学校食堂每天的用煤量一定,用煤的总量和用的天数;小麦每公顷的产量一定,总产量和公顷数……
探索新知
一个化肥厂的生产情况如下表,根据表中数据回答问题。
(1)表中有哪两种相关联的量?
(2)表中相关联的两种量成正比例吗?为什么
时间和生产量是两种相关联的量。
成正比例,因为生产量随着时间的增多(减少)而增多(减少),且生产量÷时间=生产效率(一定),所以时间和生产量成正比例。
时间(天) 1 2 3 4 5 6 7
生产量(吨) 80 160 240 320 400 480 560
易错提醒
判断:圆的半径越大,它的面积就越大,所以圆的半径和面积成正比例。( )
辨析:没有正确理解正比例关系引起的判断错误。
×
03
学以致用
小试牛刀
1.填空。
(1)为提高自身的阅读能力,学生们积极订阅书刊,认真阅读。某书店销售《小学生天地》的份数和总价如下表:
①表中( )和( )是相关联的量,( )增加,( )也随着增加。
②总价与份数这两种相关联的量中相对应的两个数的比值都是( ),这个比值实际上是( )。
③因为总价与份数的比值一定,所以表中的两种量叫做成( )的量。
份数/份 1 2 3 4 5 6 …
总价/元 30 60 90 120 150 180 …
份数
总价
份数
总价
30
每份《小学生天地》的单价
正比例
小试牛刀
1.填空。
(2)路程与时间的比值是( ),当这个比值一定时,( )和( )成( )比例关系。
速度
路程
时间
正
2.判断。(对的画“√”,错的画“×”)
(1)长方形的长一定,宽和面积成正比例关系。 ( )
(2)正方形的面积与边长成正比例关系。 ( )
(3)比的前项一定,比的后项和比值成正比例关系。( )
(4)x÷y=4,x和y成正比例关系。 ( )
√
×
×
√
小试牛刀
3.选择。(将正确答案的字母填在括号里)
(1)下列各组中两种量不成正比例关系的是( )。
A.人的身高与年龄
B.y=5x中y和x
C.工作效率一定,工作总量和工作时间
D.圆的周长与直径
(2)甲数的 与乙数的 相等(甲、乙两数均不为0),
甲数与乙数( )。 A.成正比例关系
B.不成正比例关系
C.不成比例
D.无法判断
A
A
小试牛刀
3.选择。(将正确答案的字母填在括号里)
(3)下列各式中,x和y成正比例的是( )。
A.x+y=6 B.x=6y
C.x× y=1 D.x+1=6y
B
04
课堂小结
圆的半径和面积不成正比例,但是圆的半径的平方和面积成正比例。两种量是否成正比例,要根据正比例的意义去判断。
归纳总结:
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
