【班海精品】冀教版(新)六下-第四单元 4.圆锥的特征【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)六下-第四单元 4.圆锥的特征【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览







文档简介
(共38张PPT)
圆锥的特征
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
01
03
02
04
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
01
情景导入
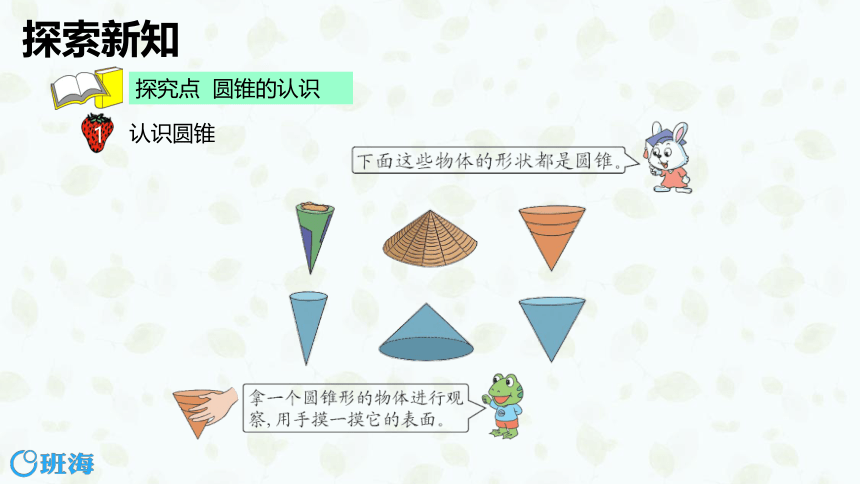
上面这些物体的形状有什么共同的特点?
新课精讲
02
探索新知
认识圆锥
1
探究点 圆锥的认识
探索新知
2 . 一起来看动画认识圆锥吧。
3 . 圆锥有哪些特点?
探索新知
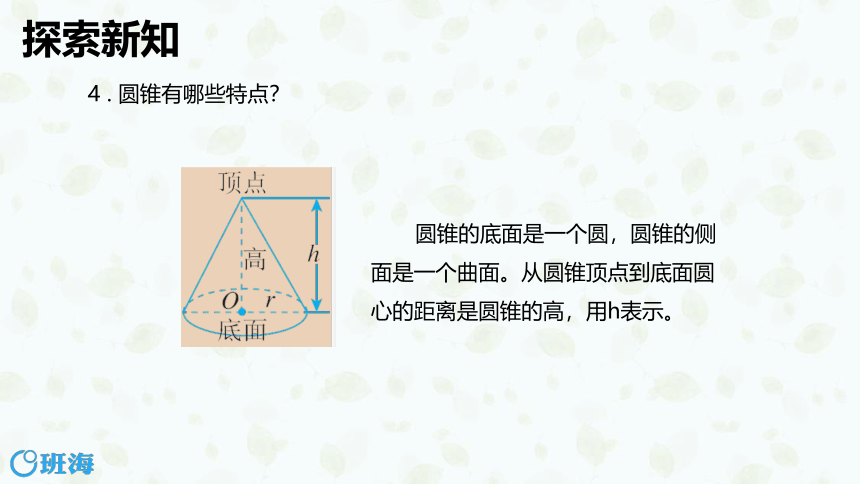
4 . 圆锥有哪些特点?
探索新知
圆锥的底面是一个圆,圆锥的侧面是一个曲面。从圆锥顶点到底面圆心的距离是圆锥的高,用h表示。
( ) ( )
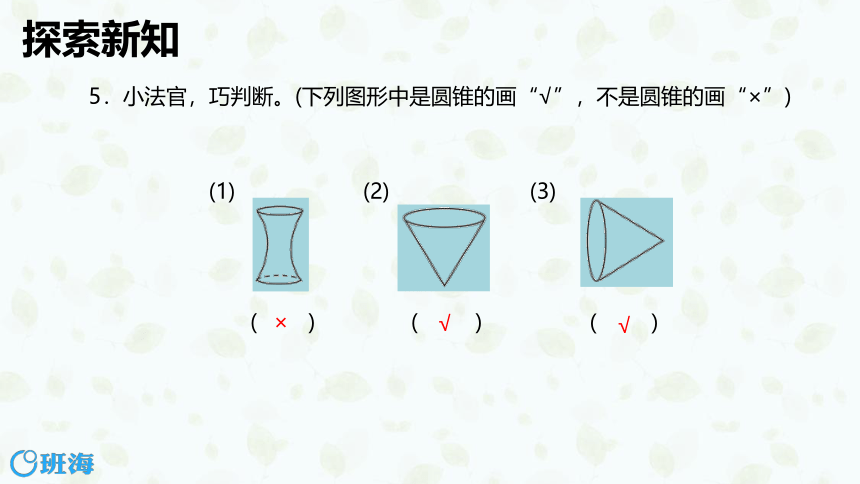
5.小法官,巧判断。(下列图形中是圆锥的画“√”,不是圆锥的画“×”)
×
(1) (2) (3)
√
√
探索新知
( )
探索新知
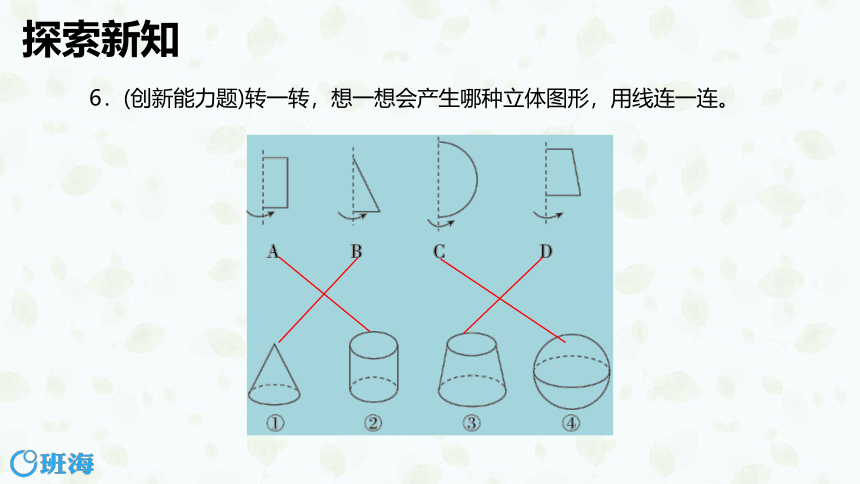
6.(创新能力题)转一转,想一想会产生哪种立体图形,用线连一连。
探索新知
(1)圆锥的底面是一个( ),圆锥的侧面是一个( )面。从圆锥的( )到( )的距离是圆锥的高。
(2)圆锥的侧面展开图是一个( )。
(3)把一个圆锥沿底面直径纵向切开平均分成两份,切面是一个( )形。
圆
曲
顶点
底面圆心
扇形
三角
7.填空。
典题精讲
小实验。
(1)找一个圆柱形杯子,再做一个和它等底等高的圆锥形容器。
(2)在圆锥形容器中装满沙子,然后倒入杯子中,看几次能倒满。
1
探究点1 圆锥体积计算公式的推导
典题精讲
(3)每倒入一次,测量一下杯子中沙子的高度,直到装满为止。边实验边填写实验记录。
实验工具 杯子:高______ 底面直径______
实验过程记录: 实验人:____
第一次 第二次
杯中沙子的高度(毫米)
实验结论:_____________________________________
日期:______月______日
实验记录
9厘米
30
60
第三次
90
3次能将圆柱形容器倒满
10厘米
典题精讲
圆锥的体积等于和它等底等高的圆柱体积的 。
如果用V表示圆锥的体积,S表示底面积,h表示高,那么圆锥的体积公式可以写成:
V= Sh
1
3
2 . 一起来讨论。
典题精讲
3 . 计算右面圆锥的体积。
×3.14×(4÷2)2×6
= ×3.14×4×6
= 25.12(cm3)
答:圆锥的体积是25.12 cm3。
典题精讲
(1)圆锥的体积等于和它( )的圆柱体积的( ),所以圆锥的体积=( ),用字母表示是( )。
(2)一个圆柱和一个圆锥等底等高。若圆柱的体积是12.6 dm3,则圆锥的体积是( )dm3;若圆锥的体积是12.6 dm3,则圆柱的体积是( )dm3。
(3)等底等高的圆柱和圆锥的体积的比是( ),圆锥的体积比圆柱的体积少( )。
等底等高
4.2
37.8
3:1
底面积×高×
Sh
4.填空。
典题精讲
5.计算下面各圆锥的体积。
42×3.14×12× =200.96(cm3)
答:圆锥的体积为200.96平方厘米。
9×3.6× =10.8(m3)
答:圆锥的体积为10.8平方米。
典题精讲
(1)一个实心铜制圆锥,底面直径是6 cm,高是3 cm。如果每立方厘米铜重8.9 g,这个实心铜制圆锥约重多少克?(得数保留整数)
(2)一个圆锥形帐篷,它的底面半径是3 m,高是2.6 m。帐篷内的空间有多大?
×3.14×3× ×8.9≈252(g)
答:这个实心铜制圆锥约重252克。
32×3.14× ×2.6=24.492(m3)
答:帐篷内的空间有24.492立方米。
6.解决问题。
典题精讲
(3)一个圆锥形小麦堆,底面周长是12.56 m,高是1.8 m。如果每立方米小麦约重780 kg,按出粉率80%计算,这堆小麦可磨出多少千克面粉?
×3.14×1.8×780×80%=4702.464(kg)
答:这个实心铜制圆锥约重252克。
典题精讲
(1)记录测量所得的数据并解决问题。
直径 (米) 周长 (米) 高 (米) 体积 (立方米) 质量
(千克)
(2)如果麦堆的周长是9.42米,高是1.2米,把这些小麦装进麻袋,每袋装90千克,那么装完这些小麦,需要多少个麻袋?
麦堆的体积: ×3.14×(9.42÷3.14÷2)2×1.2=2.826(立方米)
小麦的质量:2.826×735=2077.11(千克)
需要麻袋的数量:2077.11÷90≈24(个)
答:需要24个麻袋。
7.解决问题。
典题精讲
估算一堆小麦的质量。
8
探究点2 测量圆锥有关数据的方法
典题精讲
9 . 估算小麦堆的质量需要哪些有关数据?测量这些数据的方法是什么?
易错提醒
1 .“圆锥和圆柱一样也有无数条高”这句话对吗?为什么?
答:不对,因为从圆锥顶点到底面圆心的距离是圆锥的高,圆锥只有1条高。
辨析:没有正确理解圆锥的高的意义。
易错提醒
(1)圆柱的体积是圆锥体积的3倍。 ( )
(2)如果一个圆锥的体积是一个圆柱体积的 ,那么这个圆锥和这个圆柱一定等底等高。 ( )
(3)一个圆锥和一个圆柱的底面积相等,圆柱的高是圆锥高的3倍,这个圆锥体的体积与圆柱体积的比是1:9。 ( )
(4)一个圆锥的体积比与它等底等高的圆柱的体积小 ( )
(5)圆锥的高是圆柱高的3倍,它们体积一定相等。 ( )
×
×
√
×
×
辨析:不能正确判断圆柱与圆锥之间的体积关系。
2 . 判断。(对的画“√”,错的画“×”)
学以致用
03
小试牛刀
找出下图中哪些是圆锥。
第2个图形和第4个图形是圆锥。
小试牛刀
下面的圆柱和圆锥等底等高。已知圆柱的体积是45立方厘米,求圆锥的体积。
×45=15(立方厘米)
小试牛刀
(1)底面面积是9. 6平方米,高是2米。
(2)底面半径是5厘米,高是3. 3厘米。
(3)底面直径是6分米,高是6分米。
×9.6×2=6.4(立方米)
×3.14×52×3.3=86.35(立方厘米)
×3.14× ×6=56.52(立方分米)
3.计算下面各圆锥的体积。
小试牛刀
右图是一个铁质机器零件的示意图。(单位:厘米 )
(1)求这个机器零件的体积。
×3.14× ×4+12×2×8=229.68(立方厘米)
答:这个机器零件的体积是229.68立方厘米。
(2)已知每立方厘米的铁重7. 8克,这个机器零件重多少千克?
229.68×7.8=1791.504(克)=1.791504(千克)
答:这个机器零件重1.791504千克。
小试牛刀
5.一囤小麦,上面是圆锥形,下面是圆柱 形。已知每立方米小麦约重735千克, 这囤小麦约重多少千克?(得数保留整 千克)
[3.14×(3÷2)2×2+3.14×(3÷2)2×0.6× ]×735≈11424(千克)
答:这囤小麦约重11424千克。
小试牛刀
6. 一个近似圆锥形的煤堆,底面周长是15. 7米,高是2.4米。这堆煤约有多少吨?(得数保留整吨)
(15.7÷3.14÷2)2×3.14×2.4× ×1.4≈22(吨)
答:这堆煤约有22吨。
小试牛刀
7. 一个圆锥形沙堆,底面直径是6米,高是2.5米。这堆沙约有多少吨?(得数保留整吨)
3.14×(6÷2)2×2.5× ×1.7≈40(吨)
答:这堆沙约有40吨。
小试牛刀
8. 一个圆锥形的钢件,底面半径是1.5厘米,高是4厘米。已知每立方厘米钢约重7. 8克,这个钢件约重多少克?(得数保留整克)
3.14×1.52×4× ×7.8≈73(克)
答:这个钢件约重73克。
小试牛刀
9.一个饲料堆的底面周长是15. 7米,高是1.7米。如果每立方米的饲料大约重210千克,那么这堆饲料重多少千克?
(15.7÷3.14÷2)2×3.14×1.7× ×210≈2335(千克)
答:这堆饲料大约重2335千克。
课堂小结
04
从圆锥顶点到底面圆心的距离是圆锥的高。
归纳总结:
圆柱的体积是它等底等高的圆锥体积的3倍。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
圆锥的特征
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
01
03
02
04
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
01
情景导入
上面这些物体的形状有什么共同的特点?
新课精讲
02
探索新知
认识圆锥
1
探究点 圆锥的认识
探索新知
2 . 一起来看动画认识圆锥吧。
3 . 圆锥有哪些特点?
探索新知
4 . 圆锥有哪些特点?
探索新知
圆锥的底面是一个圆,圆锥的侧面是一个曲面。从圆锥顶点到底面圆心的距离是圆锥的高,用h表示。
( ) ( )
5.小法官,巧判断。(下列图形中是圆锥的画“√”,不是圆锥的画“×”)
×
(1) (2) (3)
√
√
探索新知
( )
探索新知
6.(创新能力题)转一转,想一想会产生哪种立体图形,用线连一连。
探索新知
(1)圆锥的底面是一个( ),圆锥的侧面是一个( )面。从圆锥的( )到( )的距离是圆锥的高。
(2)圆锥的侧面展开图是一个( )。
(3)把一个圆锥沿底面直径纵向切开平均分成两份,切面是一个( )形。
圆
曲
顶点
底面圆心
扇形
三角
7.填空。
典题精讲
小实验。
(1)找一个圆柱形杯子,再做一个和它等底等高的圆锥形容器。
(2)在圆锥形容器中装满沙子,然后倒入杯子中,看几次能倒满。
1
探究点1 圆锥体积计算公式的推导
典题精讲
(3)每倒入一次,测量一下杯子中沙子的高度,直到装满为止。边实验边填写实验记录。
实验工具 杯子:高______ 底面直径______
实验过程记录: 实验人:____
第一次 第二次
杯中沙子的高度(毫米)
实验结论:_____________________________________
日期:______月______日
实验记录
9厘米
30
60
第三次
90
3次能将圆柱形容器倒满
10厘米
典题精讲
圆锥的体积等于和它等底等高的圆柱体积的 。
如果用V表示圆锥的体积,S表示底面积,h表示高,那么圆锥的体积公式可以写成:
V= Sh
1
3
2 . 一起来讨论。
典题精讲
3 . 计算右面圆锥的体积。
×3.14×(4÷2)2×6
= ×3.14×4×6
= 25.12(cm3)
答:圆锥的体积是25.12 cm3。
典题精讲
(1)圆锥的体积等于和它( )的圆柱体积的( ),所以圆锥的体积=( ),用字母表示是( )。
(2)一个圆柱和一个圆锥等底等高。若圆柱的体积是12.6 dm3,则圆锥的体积是( )dm3;若圆锥的体积是12.6 dm3,则圆柱的体积是( )dm3。
(3)等底等高的圆柱和圆锥的体积的比是( ),圆锥的体积比圆柱的体积少( )。
等底等高
4.2
37.8
3:1
底面积×高×
Sh
4.填空。
典题精讲
5.计算下面各圆锥的体积。
42×3.14×12× =200.96(cm3)
答:圆锥的体积为200.96平方厘米。
9×3.6× =10.8(m3)
答:圆锥的体积为10.8平方米。
典题精讲
(1)一个实心铜制圆锥,底面直径是6 cm,高是3 cm。如果每立方厘米铜重8.9 g,这个实心铜制圆锥约重多少克?(得数保留整数)
(2)一个圆锥形帐篷,它的底面半径是3 m,高是2.6 m。帐篷内的空间有多大?
×3.14×3× ×8.9≈252(g)
答:这个实心铜制圆锥约重252克。
32×3.14× ×2.6=24.492(m3)
答:帐篷内的空间有24.492立方米。
6.解决问题。
典题精讲
(3)一个圆锥形小麦堆,底面周长是12.56 m,高是1.8 m。如果每立方米小麦约重780 kg,按出粉率80%计算,这堆小麦可磨出多少千克面粉?
×3.14×1.8×780×80%=4702.464(kg)
答:这个实心铜制圆锥约重252克。
典题精讲
(1)记录测量所得的数据并解决问题。
直径 (米) 周长 (米) 高 (米) 体积 (立方米) 质量
(千克)
(2)如果麦堆的周长是9.42米,高是1.2米,把这些小麦装进麻袋,每袋装90千克,那么装完这些小麦,需要多少个麻袋?
麦堆的体积: ×3.14×(9.42÷3.14÷2)2×1.2=2.826(立方米)
小麦的质量:2.826×735=2077.11(千克)
需要麻袋的数量:2077.11÷90≈24(个)
答:需要24个麻袋。
7.解决问题。
典题精讲
估算一堆小麦的质量。
8
探究点2 测量圆锥有关数据的方法
典题精讲
9 . 估算小麦堆的质量需要哪些有关数据?测量这些数据的方法是什么?
易错提醒
1 .“圆锥和圆柱一样也有无数条高”这句话对吗?为什么?
答:不对,因为从圆锥顶点到底面圆心的距离是圆锥的高,圆锥只有1条高。
辨析:没有正确理解圆锥的高的意义。
易错提醒
(1)圆柱的体积是圆锥体积的3倍。 ( )
(2)如果一个圆锥的体积是一个圆柱体积的 ,那么这个圆锥和这个圆柱一定等底等高。 ( )
(3)一个圆锥和一个圆柱的底面积相等,圆柱的高是圆锥高的3倍,这个圆锥体的体积与圆柱体积的比是1:9。 ( )
(4)一个圆锥的体积比与它等底等高的圆柱的体积小 ( )
(5)圆锥的高是圆柱高的3倍,它们体积一定相等。 ( )
×
×
√
×
×
辨析:不能正确判断圆柱与圆锥之间的体积关系。
2 . 判断。(对的画“√”,错的画“×”)
学以致用
03
小试牛刀
找出下图中哪些是圆锥。
第2个图形和第4个图形是圆锥。
小试牛刀
下面的圆柱和圆锥等底等高。已知圆柱的体积是45立方厘米,求圆锥的体积。
×45=15(立方厘米)
小试牛刀
(1)底面面积是9. 6平方米,高是2米。
(2)底面半径是5厘米,高是3. 3厘米。
(3)底面直径是6分米,高是6分米。
×9.6×2=6.4(立方米)
×3.14×52×3.3=86.35(立方厘米)
×3.14× ×6=56.52(立方分米)
3.计算下面各圆锥的体积。
小试牛刀
右图是一个铁质机器零件的示意图。(单位:厘米 )
(1)求这个机器零件的体积。
×3.14× ×4+12×2×8=229.68(立方厘米)
答:这个机器零件的体积是229.68立方厘米。
(2)已知每立方厘米的铁重7. 8克,这个机器零件重多少千克?
229.68×7.8=1791.504(克)=1.791504(千克)
答:这个机器零件重1.791504千克。
小试牛刀
5.一囤小麦,上面是圆锥形,下面是圆柱 形。已知每立方米小麦约重735千克, 这囤小麦约重多少千克?(得数保留整 千克)
[3.14×(3÷2)2×2+3.14×(3÷2)2×0.6× ]×735≈11424(千克)
答:这囤小麦约重11424千克。
小试牛刀
6. 一个近似圆锥形的煤堆,底面周长是15. 7米,高是2.4米。这堆煤约有多少吨?(得数保留整吨)
(15.7÷3.14÷2)2×3.14×2.4× ×1.4≈22(吨)
答:这堆煤约有22吨。
小试牛刀
7. 一个圆锥形沙堆,底面直径是6米,高是2.5米。这堆沙约有多少吨?(得数保留整吨)
3.14×(6÷2)2×2.5× ×1.7≈40(吨)
答:这堆沙约有40吨。
小试牛刀
8. 一个圆锥形的钢件,底面半径是1.5厘米,高是4厘米。已知每立方厘米钢约重7. 8克,这个钢件约重多少克?(得数保留整克)
3.14×1.52×4× ×7.8≈73(克)
答:这个钢件约重73克。
小试牛刀
9.一个饲料堆的底面周长是15. 7米,高是1.7米。如果每立方米的饲料大约重210千克,那么这堆饲料重多少千克?
(15.7÷3.14÷2)2×3.14×1.7× ×210≈2335(千克)
答:这堆饲料大约重2335千克。
课堂小结
04
从圆锥顶点到底面圆心的距离是圆锥的高。
归纳总结:
圆柱的体积是它等底等高的圆锥体积的3倍。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
