【班海精品】冀教版(新)五下-第五单元 6.2体积的应用问题【优质课件】
文档属性
| 名称 | 【班海精品】冀教版(新)五下-第五单元 6.2体积的应用问题【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:18:48 | ||
图片预览








文档简介
(共23张PPT)
认识面积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
学以致用
新课精讲
课堂小结
01
课前导入
情景导入
壮观的拦河坝。
02
新课精讲
探索新知
探究点 体积的实际应用
李大伯计划挖一个长是2米、宽是1.6米、深是1.5米的地窖。要挖出多少立方米的土?
2×1.6×1.5=4.8(立方米)
答:要挖出4.8立方米的土。
探索新知
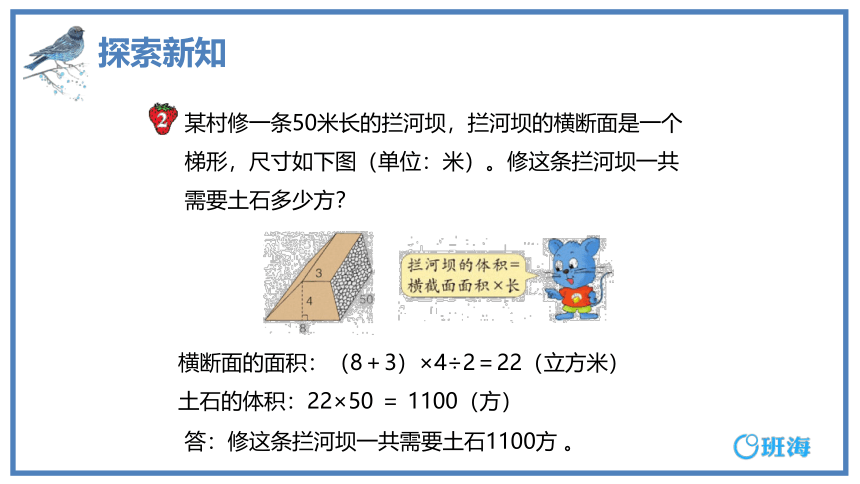
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这条拦河坝一共需要土石多少方?
横断面的面积:(8+3)×4÷2=22(立方米)
土石的体积:22×50 = 1100(方)
答:修这条拦河坝一共需要土石1100方 。
探索新知
某地有一段古墙,墙由长方体砖砌成,尺寸如下图。
自己提出数学问题,并解答。
这段古墙大约是由多少块砖砌成的?
墙的体积:(2+2)×6×0.5-2×2×0.5=10(m )
砖的体积:50 cm=0.5 m 25 cm=0.25 m 20 cm=0.2 m
0.5×0.25×0.2=0.025(m )
砖的块数:10÷0.025=400(块)
答:这段古墙大约是由400 块砖砌成的。
典题精讲
1.填一填。
(1)某地计划修一条长100米的拦河大坝,拦河大坝的横断面
是一个梯形,梯形的上底是6米,下底是18米,高是10米,
修这个拦河大坝一共要( )立方米的土石。
(2)新建的羽毛球球馆要铺设3厘米厚的木质地板,已知羽毛
球球馆的地面长是36米,宽是20米,铺设它至少要用
( )平方米的木材。
12000
21.6
典题精讲
2.计算下面立体图形的体积。(单位:厘米)
(1)
(2)
(3)
6×6×6-2×2×2=208(立方厘米)
8×10×5-5×5×3=325(立方厘米)
(20+10)×25÷2÷2×35×2=13125(立方厘米)
典题精讲
3.如下图,有一块体积是0.25立方米的石材,求这块石材的长度。
0.25÷[(0.4+0.6)×0.25÷2]=2(米)
易错提醒
判断。
(1)生活中,计量沙、土、石子等的体积时,常常把“立方米”
简称为“方”。 ( )
(2)从长方体的一个顶点处挖去一个小正方体,则与原长方体相比,现在的图形的体积和表面积都变小了。 ( )
(3)把两个棱长是4厘米的小正方体拼成一个长方体后,表面积和体积都扩大到原来的2倍。 ( )
√
×
辨析:现在图形的体积变小了,表面积没变。
辨析:体积扩大到原来的2倍,表面积没有扩大到原来的2倍。
×
03
学以致用
小试牛刀
1.下面是一根混凝土的铁路轨枕,求它的体积。
1.8 m=180 cm
(28+16)×16÷2×180=63360(cm3)
小试牛刀
2.一块长方体钢材,长是80厘米,宽是50厘米,厚是2厘米。如果这 种钢材每立方厘米重7.8克,这块钢材重多少千克?
80×50×2=8000(立方厘米)
8000×7.8=62400(克)
62400克=62.4千克
小试牛刀
3.旺山乡计划挖一条5千米长的水渠,水渠横截面是一个梯形,尺寸如下图。(单位:米)
已经挖了20米长,挖出多少方土?
(5+2)×1.5÷2×20=105(立方米)
105立方米=105方
小试牛刀
3.旺山乡计划挖一条5千米长的水渠,水渠横截面是一个梯形,尺寸如下图。(单位:米)
(2) 如果按每天挖土200方计算,修这条水渠大约要用多少天?
5千米=5000米 (5+2)×1.5÷2×5000=26250(立方米)
26250立方米=26250方 26250÷200=131.25≈132(天)
小试牛刀
4.计算下面物体的体积。(单位:厘米)
20×6×12-6×6×6=1224(立方厘米)
小试牛刀
5*.右图是由两个长方体木块粘成的物体,求这 个物体的体积和表面积。(单位:厘米)
体积:12×6×4+6×4×3=360(立方厘米)
表面积:(12×6+12×4+4×6)×2=288(平方厘米)
(6×4+6×3+4×3)×2=108(平方厘米)
288+108=396(平方厘米)
396-4×6×2=348(平方厘米)
小试牛刀
6.某单位新盖一处房子,地基的形状如下图所示,为了打墙基,需要挖宽是1米,深是0.5米的沟(阴影部分),一共要挖多少方的土?
12×8-(8-1-1)×(12-1-1)=36(平方米)
36×0.5=18(方)
04
课堂小结
堤坝土石方的计算方法
1. 生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”。
2. 求挖出多少方土石,可以根据体积公式来计算。
3. 堤坝土石方的计算方法:
拦河坝的体积=横断面面积× 长。
归纳总结:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
认识面积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
学以致用
新课精讲
课堂小结
01
课前导入
情景导入
壮观的拦河坝。
02
新课精讲
探索新知
探究点 体积的实际应用
李大伯计划挖一个长是2米、宽是1.6米、深是1.5米的地窖。要挖出多少立方米的土?
2×1.6×1.5=4.8(立方米)
答:要挖出4.8立方米的土。
探索新知
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这条拦河坝一共需要土石多少方?
横断面的面积:(8+3)×4÷2=22(立方米)
土石的体积:22×50 = 1100(方)
答:修这条拦河坝一共需要土石1100方 。
探索新知
某地有一段古墙,墙由长方体砖砌成,尺寸如下图。
自己提出数学问题,并解答。
这段古墙大约是由多少块砖砌成的?
墙的体积:(2+2)×6×0.5-2×2×0.5=10(m )
砖的体积:50 cm=0.5 m 25 cm=0.25 m 20 cm=0.2 m
0.5×0.25×0.2=0.025(m )
砖的块数:10÷0.025=400(块)
答:这段古墙大约是由400 块砖砌成的。
典题精讲
1.填一填。
(1)某地计划修一条长100米的拦河大坝,拦河大坝的横断面
是一个梯形,梯形的上底是6米,下底是18米,高是10米,
修这个拦河大坝一共要( )立方米的土石。
(2)新建的羽毛球球馆要铺设3厘米厚的木质地板,已知羽毛
球球馆的地面长是36米,宽是20米,铺设它至少要用
( )平方米的木材。
12000
21.6
典题精讲
2.计算下面立体图形的体积。(单位:厘米)
(1)
(2)
(3)
6×6×6-2×2×2=208(立方厘米)
8×10×5-5×5×3=325(立方厘米)
(20+10)×25÷2÷2×35×2=13125(立方厘米)
典题精讲
3.如下图,有一块体积是0.25立方米的石材,求这块石材的长度。
0.25÷[(0.4+0.6)×0.25÷2]=2(米)
易错提醒
判断。
(1)生活中,计量沙、土、石子等的体积时,常常把“立方米”
简称为“方”。 ( )
(2)从长方体的一个顶点处挖去一个小正方体,则与原长方体相比,现在的图形的体积和表面积都变小了。 ( )
(3)把两个棱长是4厘米的小正方体拼成一个长方体后,表面积和体积都扩大到原来的2倍。 ( )
√
×
辨析:现在图形的体积变小了,表面积没变。
辨析:体积扩大到原来的2倍,表面积没有扩大到原来的2倍。
×
03
学以致用
小试牛刀
1.下面是一根混凝土的铁路轨枕,求它的体积。
1.8 m=180 cm
(28+16)×16÷2×180=63360(cm3)
小试牛刀
2.一块长方体钢材,长是80厘米,宽是50厘米,厚是2厘米。如果这 种钢材每立方厘米重7.8克,这块钢材重多少千克?
80×50×2=8000(立方厘米)
8000×7.8=62400(克)
62400克=62.4千克
小试牛刀
3.旺山乡计划挖一条5千米长的水渠,水渠横截面是一个梯形,尺寸如下图。(单位:米)
已经挖了20米长,挖出多少方土?
(5+2)×1.5÷2×20=105(立方米)
105立方米=105方
小试牛刀
3.旺山乡计划挖一条5千米长的水渠,水渠横截面是一个梯形,尺寸如下图。(单位:米)
(2) 如果按每天挖土200方计算,修这条水渠大约要用多少天?
5千米=5000米 (5+2)×1.5÷2×5000=26250(立方米)
26250立方米=26250方 26250÷200=131.25≈132(天)
小试牛刀
4.计算下面物体的体积。(单位:厘米)
20×6×12-6×6×6=1224(立方厘米)
小试牛刀
5*.右图是由两个长方体木块粘成的物体,求这 个物体的体积和表面积。(单位:厘米)
体积:12×6×4+6×4×3=360(立方厘米)
表面积:(12×6+12×4+4×6)×2=288(平方厘米)
(6×4+6×3+4×3)×2=108(平方厘米)
288+108=396(平方厘米)
396-4×6×2=348(平方厘米)
小试牛刀
6.某单位新盖一处房子,地基的形状如下图所示,为了打墙基,需要挖宽是1米,深是0.5米的沟(阴影部分),一共要挖多少方的土?
12×8-(8-1-1)×(12-1-1)=36(平方米)
36×0.5=18(方)
04
课堂小结
堤坝土石方的计算方法
1. 生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”。
2. 求挖出多少方土石,可以根据体积公式来计算。
3. 堤坝土石方的计算方法:
拦河坝的体积=横断面面积× 长。
归纳总结:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
