7.3 平行线的性质同步练习（含答案）

中小学教育资源及组卷应用平台
第七章 相交线与平行线
7.3 平行线的性质
基础夯实逐点练
知识点一 平行线的性质
1.如图,a∥b,∠1=60°,则∠2的大小是 ( )
A.60° B.80° C.100° D.120°
2.如图，小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上，并测得∠1=23°,则∠2的度数是 ( )
A.23° B.22° C.37° D.67°
3.一副直角三角板如图所示摆放，它们的直角顶点重合于点O,CO∥AB,则∠BOD=( )
A.30° B.45° C.60° D.90°
4.如图,AB∥CD,直线EF 与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P，下列结论错误的是( )
A.∠CNH=∠BPG B.∠BMN=∠MNC C.∠DNG=∠AME D.∠EMB=∠END
5.(烟台莱阳期末)如图，已知AB∥CD,射线DE平分∠BDC交AB于点E,∠1=50°,则∠2的度数是 .
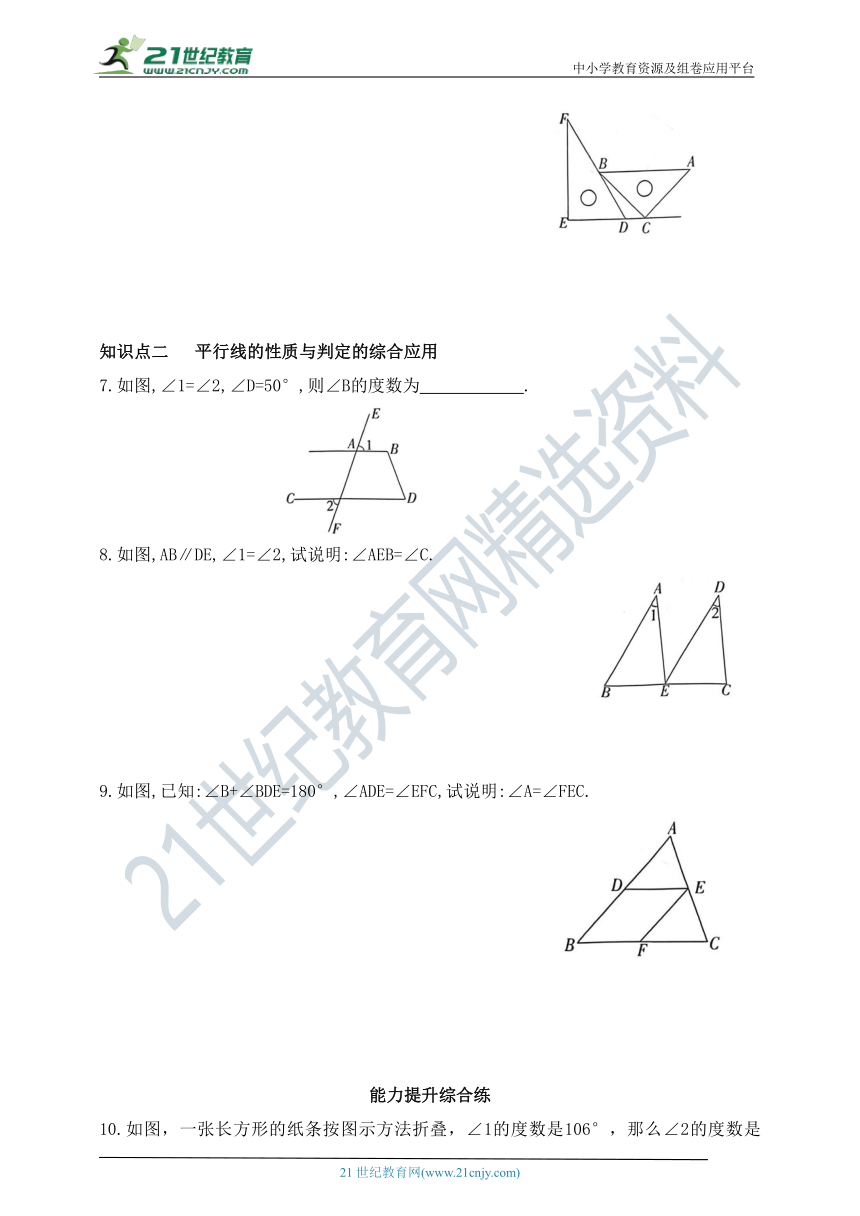
一副直角三角板如图放置，点B 在DF上,点C在ED的延长线上,AB∥CE,∠E=∠ACB=90°,求∠DBC的度数.
知识点二 平行线的性质与判定的综合应用
7.如图,∠1=∠2,∠D=50°,则∠B的度数为 .
8.如图,AB∥DE,∠1=∠2,试说明:∠AEB=∠C.
9.如图,已知:∠B+∠BDE=180°,∠ADE=∠EFC,试说明:∠A=∠FEC.
能力提升综合练
10.如图，一张长方形的纸条按图示方法折叠，∠1的度数是106°，那么∠2的度数是 ( )
A.106° B.116° C.117° D.127°
11.如图,AB∥CD∥EF,CF平分∠AFE,∠A =30°,则∠C的度数是 .
12.如图,AB∥CD,BE平分∠ABC交CD于点D,∠CDE=150°,求∠C的度数.
13.如图,AB∥EF,CD∥EF,点P在直线EF 上,且满足∠ABP=100°,∠DCP=130°,求∠1的度数.
14.如图,已知AD∥BE,∠1=∠2,∠3=∠4,试说明:AB∥CD.
15.如图,AB∥CD,CD和BE相交于点O,DE 平分∠CDF,DE和BE相交于点E,∠E=∠2.试说明:∠B=2∠2.
核心素养拓展练
16.如图,已知AB∥CD,CE平分∠ACD,CF ⊥CE,∠1=34°.
(1)求∠ACE的度数;
(2)若∠2=56°,求证:CF∥AG.
参考答案
基础夯实逐点练
1.D 2.C 3.C
4.C 【解析】∵AB∥CD,∴∠CNH=∠APN,∵∠APN=∠BPG,∴∠CNH=∠BPG,结论正确,故A不符合题意;∵AB∥CD,∴∠BMN=∠MNC,结论正确,故B不符合题意;∵AB∥CD,∴∠DNG=∠BPG,∵∠BPG≠∠AME,∴∠DNG≠∠AME,结论错误,故C符合题意;∵AB∥CD,∴∠EMB=∠END,结论正确,故D不符合题意.故选C.
5.80° 【解析】∵AB∥CD.∠1=50°,∴∠EDC=∠1=50°.
∵DE平分∠BDC,∴∠BDC=2∠EDC=100°.
∵AB∥CD,∴∠2+∠BDC=180°,∴∠2=180°-∠BDC=180°-100°=80°.
6.解:∵AB∥CE,∠EDF=60°,(已知)
∴∠DBA=∠EDF=60°(两直线平行,内错角相等).
∵∠ABC=45°(已知),∴∠DBC=∠DBA-∠ABC=60°-45°=15°.
7.130°
8.解:∵AB∥DE(已知),∴∠1=∠AED(两直线平行,内错角相等).
∵∠1=∠2(已知),∴∠2=∠AED(等量代换),
∴AE∥DC(内错角相等,两直线平行),
∴∠AEB=∠C(两直线平行,同位角相等).
9.解:∵∠B+∠BDE=180°(已知),
∴DE∥BC(同旁内角互补，两直线平行)，
∴∠EFC=∠DEF(两直线平行,内错角相等).
∵∠ADE=∠EFC(已知),∴∠ADE=∠DEF(等量代换),
∴AB∥EF(内错角相等,两直线平行).
∴∠A=∠FEC(两直线平行,同位角相等).
能力提升综合练
10.D 【解析】如图所示:∵∠1=106°,∴∠3=180°-106°=74°.
由折叠的性质得,∠4=∠5,∵∠3+∠4+∠5=
180°-53°=127°.故选D.
11.15° 【解析】∵AB∥EF,∴∠A=∠AFE=30°.
∵FC平分15°.
∵CD∥EF,∴∠C=∠CFE=15°.
12.解:∵∠CDE=150°,∴∠CDB=180°-∠CDE=30°.
∵AB∥CD,∴∠ABD=∠CDB=30°.
∵BE平分∠ABC,∴∠ABC=2∠CBD=2×30°=60°,
∴∠C=180°-∠ABC=180°-60°=120°.
13.解:∵AB∥EF,CD∥EF,
∴∠BPE=180°-∠ABP=180°-100°=80°,∠CPF=180°-∠DCP=180°-130°=50°,
∴∠1=180°-∠BPE-∠CPF=180°-80°-50°=50°.
14.解:∵AD∥BE(已知),∴∠3=∠CAD(两直线平行,内错角相等).
∵∠3=∠4(已知),∴∠4=∠CAD(等量代换).
∵∠1=∠2(已知),∴∠1+∠CAE=∠2+∠CAE(等式的性质),即∠BAE=∠CAD,
∴∠4=∠BAE(等量代换),
∴AB∥CD(同位角相等,两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)