第七章 相交线与平行线单元检测题(含答案)
文档属性
| 名称 | 第七章 相交线与平行线单元检测题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章综合检测题
(时间:90分钟 分值:150分)
一、选择题(每小题4分,共48分)
1.如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是( )
A.两点确定一条直线
B.经过一点有且只有一条直线与已知直线垂直
C.过一点只能作一直线
D.垂线段最短
2.在乡村振兴活动中,某村通过铺设水管将河水引到村庄C处,为节省材料,如图所示,他们过点C向河岸l作垂线,垂足为点D,于是确定沿CD铺设水管,这样做的数学道理是( )
A.两点之间,线段最短
B.过一点有且只有一条直线与已知直线垂直
C.垂线段最短
D.两条直线相交有且只有一个交点
3.如图,l是l 与l 的截线.找出∠1的同位角,标上∠2,找出∠1的同旁内角,标上∠3.∠1,∠2,∠3正确的位置图是( )
4.两直线相交形成的4个角的度数之比依次可能是 ( )
A.2 :3 :2 :3 B.1 :1 :4 :4
C.1 :2 :3 :4 D.3 :4 :4 :3
5.如图,桌面上有木条b,c固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )
A.20 B.30 C.70 D.80
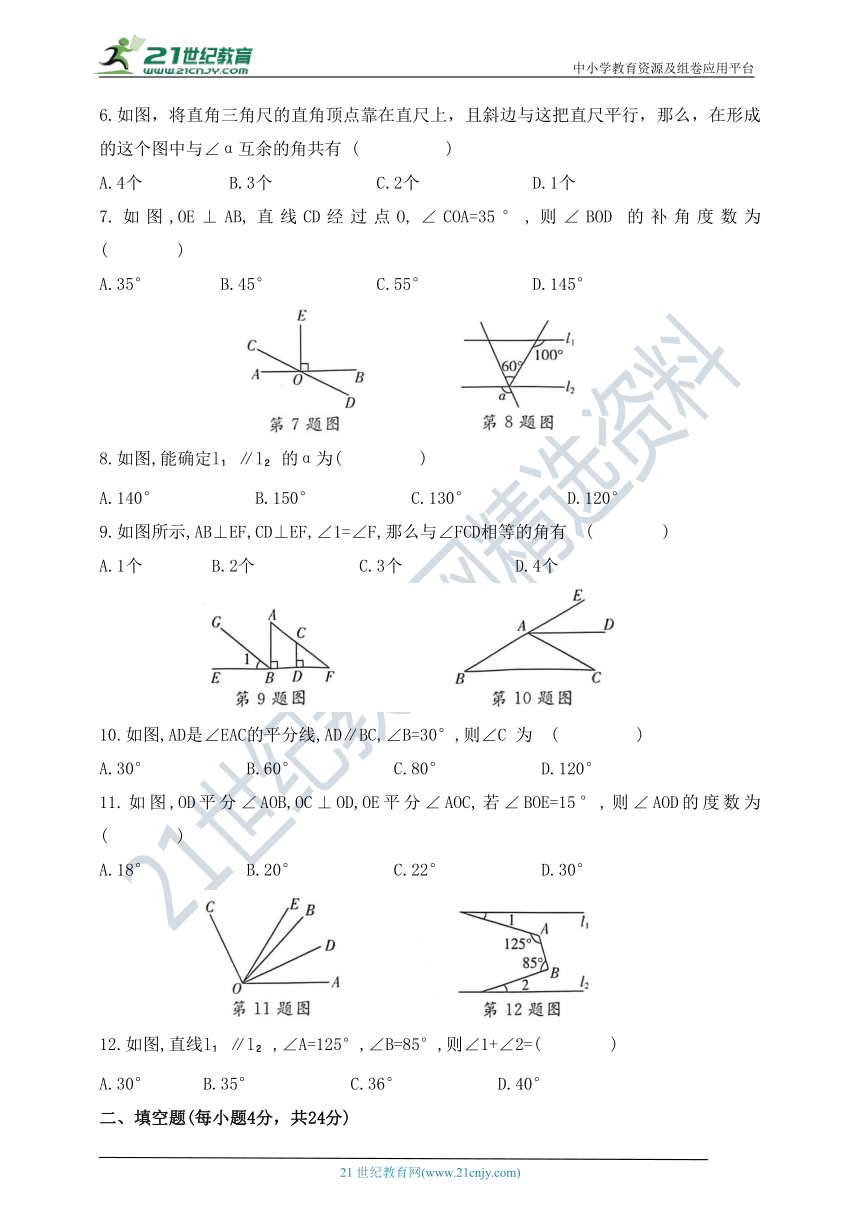
6.如图,将直角三角尺的直角顶点靠在直尺上,且斜边与这把直尺平行,那么,在形成的这个图中与∠α互余的角共有 ( )
A.4个 B.3个 C.2个 D.1个
7.如图,OE⊥AB,直线CD经过点O,∠COA=35°,则∠BOD 的补角度数为 ( )
A.35° B.45° C.55° D.145°
8.如图,能确定l ∥l 的α为( )
A.140° B.150° C.130° D.120°
9.如图所示,AB⊥EF,CD⊥EF,∠1=∠F,那么与∠FCD相等的角有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C 为 ( )
A.30° B.60° C.80° D.120°
11.如图,OD平分∠AOB,OC⊥OD,OE平分∠AOC,若∠BOE=15°,则∠AOD的度数为 ( )
A.18° B.20° C.22° D.30°
12.如图,直线l ∥l ,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
二、填空题(每小题4分,共24分)
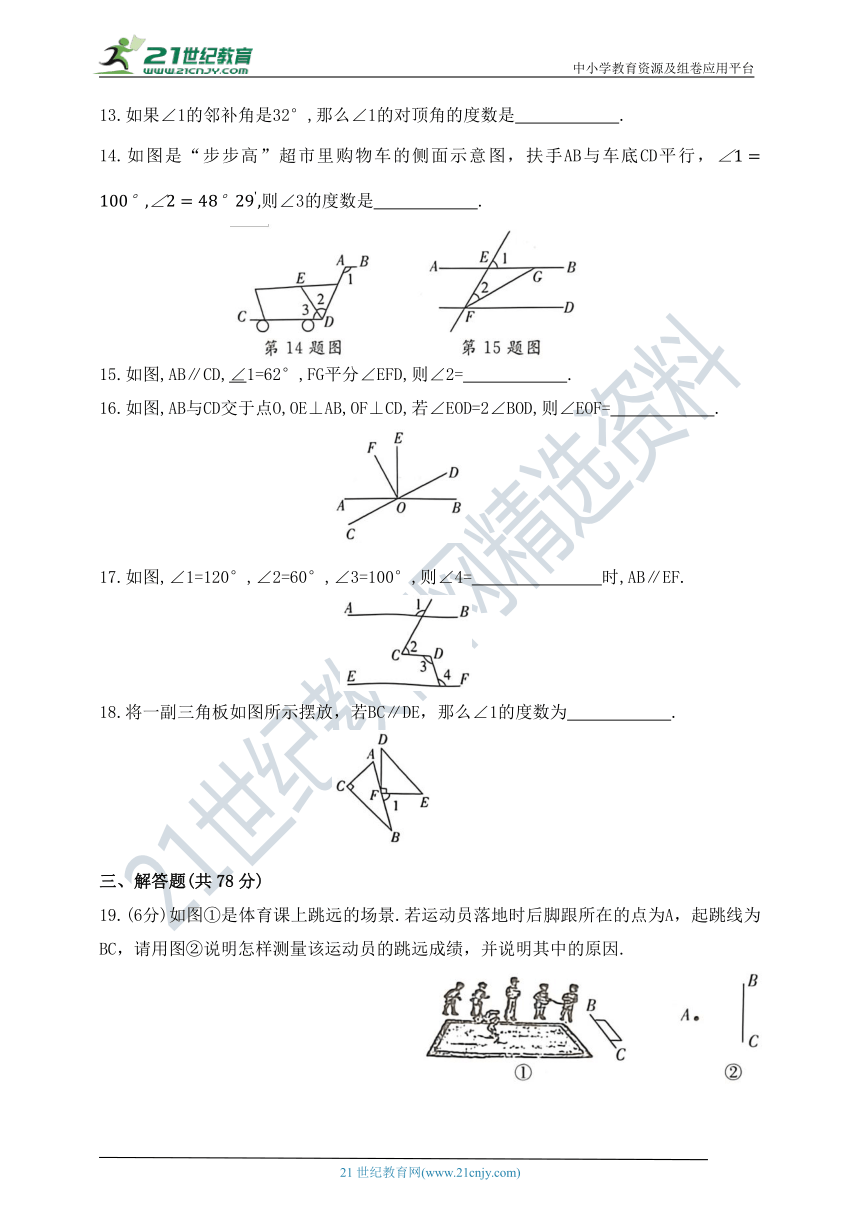
13.如果∠1的邻补角是32°,那么∠1的对顶角的度数是 .
14.如图是“步步高”超市里购物车的侧面示意图,扶手AB与车底CD平行,则∠3的度数是 .
15.如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2= .
16.如图,AB与CD交于点O,OE⊥AB,OF⊥CD,若∠EOD=2∠BOD,则∠EOF= .
17.如图,∠1=120°,∠2=60°,∠3=100°,则∠4= 时,AB∥EF.
18.将一副三角板如图所示摆放,若BC∥DE,那么∠1的度数为 .
三、解答题(共78分)
19.(6分)如图①是体育课上跳远的场景.若运动员落地时后脚跟所在的点为A,起跳线为BC,请用图②说明怎样测量该运动员的跳远成绩,并说明其中的原因.
20.(8分)如图,光线CO照射到镜面AB上的O点,请你用直尺和圆规作出CO经过镜面反射后的光线.
(不写作法,但保留作图痕迹)
21.(10分)如图,已知直线AB,CD交于点O,OE平分∠AOC,OF平分∠BOD,
(1)试说明:∠COE=∠DOF.
(2)问:OE,OF在一条直线上吗 为什么
22.(12分)如图,直线AB,CD相交于点O,OE是∠COB的平分线,FO⊥OE,已知∠AOD=70°.
(1)求∠BOE的度数.
(2)OF平分∠AOC吗 为什么
23.(14分)如图,已知BA平分∠EBC,CD平分∠ACF,且AB∥CD.
(1)试判断AC与BE的位置关系,并说明理由.
(2)若DC⊥EC,垂足为点C,猜想∠E与∠FCD之间的关系,并证明你的猜想.
24.(14分)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°.
(1)求∠EDC的度数.
(2)过E作EF∥AB,若∠BCD=40°,试求∠BED的度数.
25.(14分)如图,已知PM∥AN,且∠A=50°,点C是射线AN 上一动点(不与点A重合),PB,PD分别平分∠APC和∠MPC,交射线AN于点B,D.
(1)求∠BPD的度数.
(2)当点C运动到使∠PBA=∠APD时,求∠APB的度数.
(3)在点C运动过程中,∠PCA与∠PDA之间是否存在一定数量关系 若存在,请写出它们之间的数量关系,并说明理由;若不存在,请举出反例.
参考答案
1.B 2.C 3.C 4.A
5.B 【解析】∵a∥b,∴一对内错角应该都为70°.
∵100°-70°=30°.∴木条a在桌面上绕点O旋转旋转30°后与b平行.故选B.
6.C 【解析】∵斜边与这把直尺平行,∴∠α=∠2.
又∵∠1+∠2=90°,∴∠1+∠α=90°.
又∵∠α+∠3=90°,∴与∠α互余的角为∠1和∠3.故选C.
7.D 【解析】∵∠BOD与∠COA是对顶角,∴∠BOD=∠COA.∵∠COA=35°,∴∠BOD=35°,∴∠BOD的补角度数:180°-35°=145°.故选D.
8.A
9.B 【解析】∵AB⊥EF,CD⊥EF,∴AB∥CD,∴∠FCD=∠A.
∵∠1=∠F,∴BG∥AF.∴∠A=∠ABG,∴与∠FCD相等的角有∠A和∠ABG.故选B.
10.A 【解析】∵AD∥BC,∠B=30°,∴∠EAD=∠B=30°.
∵AD是∠EAC的平分线,∴∠DAC=∠EAD=30°.
∴∠C=∠DAC=30°.故选A.
11.B 【解析】∵OC⊥OD,∴∠COD=90°,∴∠AOC=∠COD+∠AOD=90°+∠AOD.
∵OD平分∠AOB,OE平分∠AOC,∠BOE=15°,
解得∠AOD=20°.
故选B.
12.A 【解析】如图,过点A作l 的平行线,过点B作l 的平行线,则∠3=∠1,∠4=∠2.∵l ∥l ,∴AC∥BD.∴∠CAB+∠ABD=180°.
∴∠3+∠4=125°+85°-180°=30°.∴∠1+∠2=30°,故选A.
13.148°
14.51°31′ 【解析】∵AB∥CD,∴∠1=100°,∠2=48°29′.
∴∠3+∠2=∠1,∴∠3=∠1-∠2=100°-48°29′=51赌31′。
15.31° 【解析】∵AB∥CD,∴∠EFD=∠1=62°.
∵FG平分
16.30° 【解析】∵OE⊥AB,∴∠EOB=90°,∴∠EOD+∠BOD=90°.
又∵∠EOD=2∠BOD,∴∠EOB=∠EOD+∠BOD=3∠BOD,
∴∠BOD=∠EOD=×90°=30°,∠EOD=60°.
∵OF⊥CD,∴∠FOD=90°,∴∠EOF=∠FOD-∠EOD=90°-60°=30°.
17.100° 【解析】当∠4=100°时,AB∥EF.
理由:∵∠3=100°,∠4=100°,∴DC∥EF.∵∠1=120°,∴∠5=60°.
∵∠2=60°,∴AB∥CD.∴AB∥EF.
18.75° 【解析】如图,作FG∥BC,则DE∥FG∥BC.
∴∠EFG=∠E=45°,∠BFG=∠B=30°.
∴∠1=∠BFG+∠EFG=30°+45°=75°.
19.解:如图所示,过点A作AE⊥BC于点E,AE的长就是该运动员的跳远成绩.
理由:点到直线的距离是指直线外一点到直线的垂线段的长度.
20.解:如图所示:
21.解:(1)∵直线AB,CD交于点O,∴∠AOC与∠BOD是对顶角,∴∠AOC=∠BOD.
∵OE平分∠AOC,OF平分∠BOD,
∴∠COE=∠DOF.
(2)∵OE平分∠AOC,∴∠AOE=∠COE,∴∠COE=∠DOF,
∴∠AOE+∠AOF=∠COE+∠AOE+∠AOD=180°,∴OE,OF在一条直线上.
22.解:(1)∵∠AOD与∠BOC是对顶角,∠AOD=70°,∴∠BOC=∠AOD=70°.
∵OE是∠COB的平分线,
(2)OF平分∠AOC.理由如下:
∵∠AOD=70°,∴∠AOC=110°,∴∠FOC=90°-∠COE=90°-35°=55°,
∴∠AOF=180° -∠AOD-∠FOC=180°-70°-55° =55° ,
∴∠FOC=∠AOF,∴OF平分∠AOC.
23.解:(1)AC∥BE.理由如下:
∵BA平分∠EBC,CD平分∠ACF,∴∠EBA=∠CBA=
∵AB∥CD,∴∠CBA=∠FCD,∴∠EBC=∠ACF,∴AC∥BE.
(2)∠E与∠FCD互余.理由如下:
∵AC∥BE,∴∠E=∠ACE.
∵CD平分∠ACF,∴∠ACD=∠FCD.
∵DC⊥EC,∴∠ACE+∠ACD=90°,
∴∠E+∠FCD=90°,即∠E与∠FCD互余.
24.解:(1)∵AB∥CD,∠BAD=70°,∴∠ADC=∠BAD=70°.
∵DE平分ADC,
(2)∵AB∥CD,∠BCD=40°,∴∠ABC=∠BCD=40°.
∵BE平分∠ABC,∴∠ABE=20°.
∵AB∥EF,AB∥CD,∴∠BEF=∠ABE=20°,EF∥CD,∴∠FED=∠EDC=35°,
∴∠BED=∠BEF+∠DEF=20°+35°=55°.
25.解:(1)∵PM∥AN,∴∠A+∠APM=180°.
∵∠A=50°,∴∠APM=180°-∠A=180°-50°=130°.
∵PB,PD分别平分∠APC和∠MPC,
130°=65°.
(2)∵PM∥AN,∴∠PBA=∠BPM.
∵∠PBA=∠APD,∴∠BPM=∠APD,∴∠APB=∠MPD.
由(1)得∠APM=130°,∠BPD=65°,
(3)存在,∠PCA=2∠PDA,理由如下:
∵PM∥AN,∴∠ACP=∠CPM,∠PDA=∠DPM.
∵PD平分∠MPC,∴∠CPM=2∠DPM,∴∠PCA=2∠PDA.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章综合检测题
(时间:90分钟 分值:150分)
一、选择题(每小题4分,共48分)
1.如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是( )
A.两点确定一条直线
B.经过一点有且只有一条直线与已知直线垂直
C.过一点只能作一直线
D.垂线段最短
2.在乡村振兴活动中,某村通过铺设水管将河水引到村庄C处,为节省材料,如图所示,他们过点C向河岸l作垂线,垂足为点D,于是确定沿CD铺设水管,这样做的数学道理是( )
A.两点之间,线段最短
B.过一点有且只有一条直线与已知直线垂直
C.垂线段最短
D.两条直线相交有且只有一个交点
3.如图,l是l 与l 的截线.找出∠1的同位角,标上∠2,找出∠1的同旁内角,标上∠3.∠1,∠2,∠3正确的位置图是( )
4.两直线相交形成的4个角的度数之比依次可能是 ( )
A.2 :3 :2 :3 B.1 :1 :4 :4
C.1 :2 :3 :4 D.3 :4 :4 :3
5.如图,桌面上有木条b,c固定,木条a在桌面上绕点O旋转n°(0<n<90)后与b平行,则n=( )
A.20 B.30 C.70 D.80
6.如图,将直角三角尺的直角顶点靠在直尺上,且斜边与这把直尺平行,那么,在形成的这个图中与∠α互余的角共有 ( )
A.4个 B.3个 C.2个 D.1个
7.如图,OE⊥AB,直线CD经过点O,∠COA=35°,则∠BOD 的补角度数为 ( )
A.35° B.45° C.55° D.145°
8.如图,能确定l ∥l 的α为( )
A.140° B.150° C.130° D.120°
9.如图所示,AB⊥EF,CD⊥EF,∠1=∠F,那么与∠FCD相等的角有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C 为 ( )
A.30° B.60° C.80° D.120°
11.如图,OD平分∠AOB,OC⊥OD,OE平分∠AOC,若∠BOE=15°,则∠AOD的度数为 ( )
A.18° B.20° C.22° D.30°
12.如图,直线l ∥l ,∠A=125°,∠B=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
二、填空题(每小题4分,共24分)
13.如果∠1的邻补角是32°,那么∠1的对顶角的度数是 .
14.如图是“步步高”超市里购物车的侧面示意图,扶手AB与车底CD平行,则∠3的度数是 .
15.如图,AB∥CD,∠1=62°,FG平分∠EFD,则∠2= .
16.如图,AB与CD交于点O,OE⊥AB,OF⊥CD,若∠EOD=2∠BOD,则∠EOF= .
17.如图,∠1=120°,∠2=60°,∠3=100°,则∠4= 时,AB∥EF.
18.将一副三角板如图所示摆放,若BC∥DE,那么∠1的度数为 .
三、解答题(共78分)
19.(6分)如图①是体育课上跳远的场景.若运动员落地时后脚跟所在的点为A,起跳线为BC,请用图②说明怎样测量该运动员的跳远成绩,并说明其中的原因.
20.(8分)如图,光线CO照射到镜面AB上的O点,请你用直尺和圆规作出CO经过镜面反射后的光线.
(不写作法,但保留作图痕迹)
21.(10分)如图,已知直线AB,CD交于点O,OE平分∠AOC,OF平分∠BOD,
(1)试说明:∠COE=∠DOF.
(2)问:OE,OF在一条直线上吗 为什么
22.(12分)如图,直线AB,CD相交于点O,OE是∠COB的平分线,FO⊥OE,已知∠AOD=70°.
(1)求∠BOE的度数.
(2)OF平分∠AOC吗 为什么
23.(14分)如图,已知BA平分∠EBC,CD平分∠ACF,且AB∥CD.
(1)试判断AC与BE的位置关系,并说明理由.
(2)若DC⊥EC,垂足为点C,猜想∠E与∠FCD之间的关系,并证明你的猜想.
24.(14分)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°.
(1)求∠EDC的度数.
(2)过E作EF∥AB,若∠BCD=40°,试求∠BED的度数.
25.(14分)如图,已知PM∥AN,且∠A=50°,点C是射线AN 上一动点(不与点A重合),PB,PD分别平分∠APC和∠MPC,交射线AN于点B,D.
(1)求∠BPD的度数.
(2)当点C运动到使∠PBA=∠APD时,求∠APB的度数.
(3)在点C运动过程中,∠PCA与∠PDA之间是否存在一定数量关系 若存在,请写出它们之间的数量关系,并说明理由;若不存在,请举出反例.
参考答案
1.B 2.C 3.C 4.A
5.B 【解析】∵a∥b,∴一对内错角应该都为70°.
∵100°-70°=30°.∴木条a在桌面上绕点O旋转旋转30°后与b平行.故选B.
6.C 【解析】∵斜边与这把直尺平行,∴∠α=∠2.
又∵∠1+∠2=90°,∴∠1+∠α=90°.
又∵∠α+∠3=90°,∴与∠α互余的角为∠1和∠3.故选C.
7.D 【解析】∵∠BOD与∠COA是对顶角,∴∠BOD=∠COA.∵∠COA=35°,∴∠BOD=35°,∴∠BOD的补角度数:180°-35°=145°.故选D.
8.A
9.B 【解析】∵AB⊥EF,CD⊥EF,∴AB∥CD,∴∠FCD=∠A.
∵∠1=∠F,∴BG∥AF.∴∠A=∠ABG,∴与∠FCD相等的角有∠A和∠ABG.故选B.
10.A 【解析】∵AD∥BC,∠B=30°,∴∠EAD=∠B=30°.
∵AD是∠EAC的平分线,∴∠DAC=∠EAD=30°.
∴∠C=∠DAC=30°.故选A.
11.B 【解析】∵OC⊥OD,∴∠COD=90°,∴∠AOC=∠COD+∠AOD=90°+∠AOD.
∵OD平分∠AOB,OE平分∠AOC,∠BOE=15°,
解得∠AOD=20°.
故选B.
12.A 【解析】如图,过点A作l 的平行线,过点B作l 的平行线,则∠3=∠1,∠4=∠2.∵l ∥l ,∴AC∥BD.∴∠CAB+∠ABD=180°.
∴∠3+∠4=125°+85°-180°=30°.∴∠1+∠2=30°,故选A.
13.148°
14.51°31′ 【解析】∵AB∥CD,∴∠1=100°,∠2=48°29′.
∴∠3+∠2=∠1,∴∠3=∠1-∠2=100°-48°29′=51赌31′。
15.31° 【解析】∵AB∥CD,∴∠EFD=∠1=62°.
∵FG平分
16.30° 【解析】∵OE⊥AB,∴∠EOB=90°,∴∠EOD+∠BOD=90°.
又∵∠EOD=2∠BOD,∴∠EOB=∠EOD+∠BOD=3∠BOD,
∴∠BOD=∠EOD=×90°=30°,∠EOD=60°.
∵OF⊥CD,∴∠FOD=90°,∴∠EOF=∠FOD-∠EOD=90°-60°=30°.
17.100° 【解析】当∠4=100°时,AB∥EF.
理由:∵∠3=100°,∠4=100°,∴DC∥EF.∵∠1=120°,∴∠5=60°.
∵∠2=60°,∴AB∥CD.∴AB∥EF.
18.75° 【解析】如图,作FG∥BC,则DE∥FG∥BC.
∴∠EFG=∠E=45°,∠BFG=∠B=30°.
∴∠1=∠BFG+∠EFG=30°+45°=75°.
19.解:如图所示,过点A作AE⊥BC于点E,AE的长就是该运动员的跳远成绩.
理由:点到直线的距离是指直线外一点到直线的垂线段的长度.
20.解:如图所示:
21.解:(1)∵直线AB,CD交于点O,∴∠AOC与∠BOD是对顶角,∴∠AOC=∠BOD.
∵OE平分∠AOC,OF平分∠BOD,
∴∠COE=∠DOF.
(2)∵OE平分∠AOC,∴∠AOE=∠COE,∴∠COE=∠DOF,
∴∠AOE+∠AOF=∠COE+∠AOE+∠AOD=180°,∴OE,OF在一条直线上.
22.解:(1)∵∠AOD与∠BOC是对顶角,∠AOD=70°,∴∠BOC=∠AOD=70°.
∵OE是∠COB的平分线,
(2)OF平分∠AOC.理由如下:
∵∠AOD=70°,∴∠AOC=110°,∴∠FOC=90°-∠COE=90°-35°=55°,
∴∠AOF=180° -∠AOD-∠FOC=180°-70°-55° =55° ,
∴∠FOC=∠AOF,∴OF平分∠AOC.
23.解:(1)AC∥BE.理由如下:
∵BA平分∠EBC,CD平分∠ACF,∴∠EBA=∠CBA=
∵AB∥CD,∴∠CBA=∠FCD,∴∠EBC=∠ACF,∴AC∥BE.
(2)∠E与∠FCD互余.理由如下:
∵AC∥BE,∴∠E=∠ACE.
∵CD平分∠ACF,∴∠ACD=∠FCD.
∵DC⊥EC,∴∠ACE+∠ACD=90°,
∴∠E+∠FCD=90°,即∠E与∠FCD互余.
24.解:(1)∵AB∥CD,∠BAD=70°,∴∠ADC=∠BAD=70°.
∵DE平分ADC,
(2)∵AB∥CD,∠BCD=40°,∴∠ABC=∠BCD=40°.
∵BE平分∠ABC,∴∠ABE=20°.
∵AB∥EF,AB∥CD,∴∠BEF=∠ABE=20°,EF∥CD,∴∠FED=∠EDC=35°,
∴∠BED=∠BEF+∠DEF=20°+35°=55°.
25.解:(1)∵PM∥AN,∴∠A+∠APM=180°.
∵∠A=50°,∴∠APM=180°-∠A=180°-50°=130°.
∵PB,PD分别平分∠APC和∠MPC,
130°=65°.
(2)∵PM∥AN,∴∠PBA=∠BPM.
∵∠PBA=∠APD,∴∠BPM=∠APD,∴∠APB=∠MPD.
由(1)得∠APM=130°,∠BPD=65°,
(3)存在,∠PCA=2∠PDA,理由如下:
∵PM∥AN,∴∠ACP=∠CPM,∠PDA=∠DPM.
∵PD平分∠MPC,∴∠CPM=2∠DPM,∴∠PCA=2∠PDA.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
