5.1.1 相交线同步练习(含答案)
文档属性
| 名称 | 5.1.1 相交线同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 294.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-29 00:00:00 | ||
图片预览


文档简介
5.1 相交线
第1课时 相交线
夯基训练
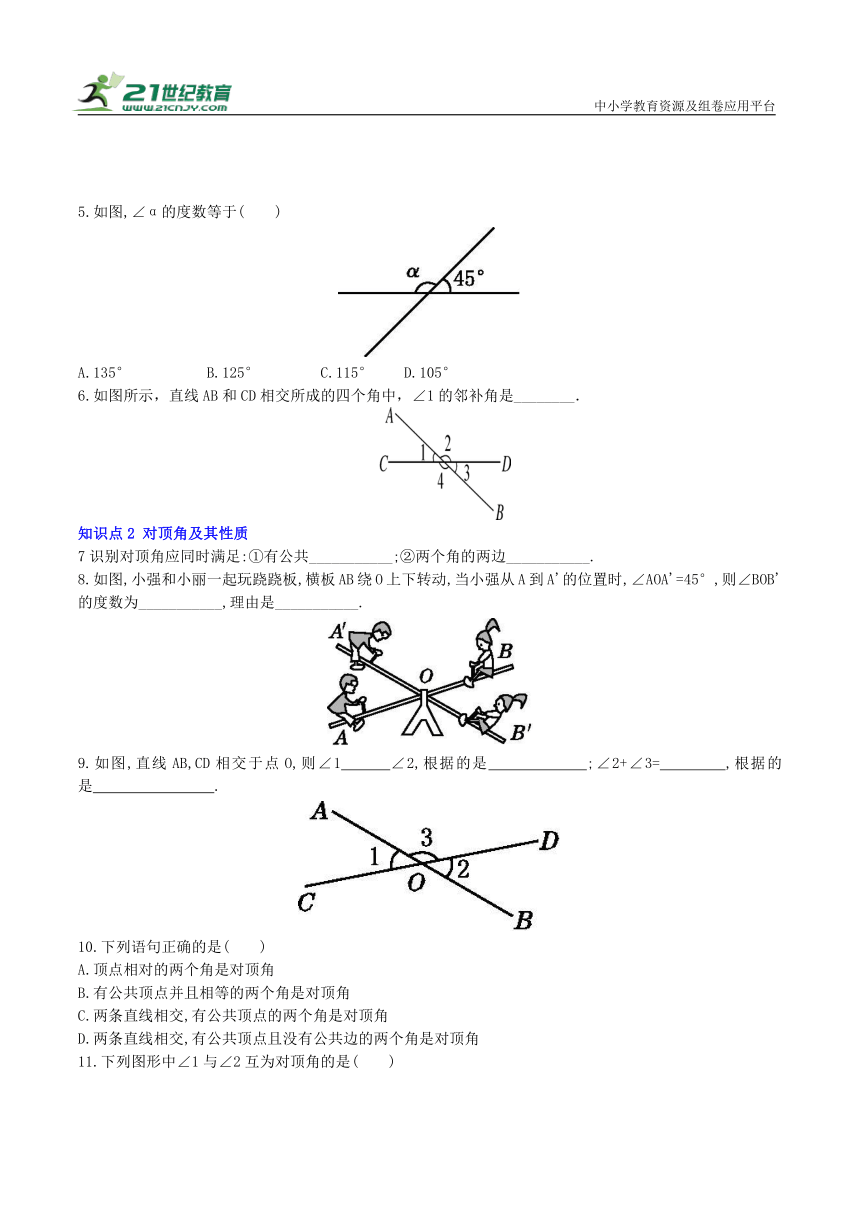
知识点1 邻补角
1.识别邻补角应同时满足以下三条:①有公共_____________;②有一条公共边;③两角的另一边_____________. 2
2.邻补角是指( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且相等的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
3.下列选项中,∠1与∠2互为邻补角的是( )
4.如图,∠1的邻补角是( )
A.∠BOC B.∠BOE和∠AOF
C.∠AOF D.∠BOC和∠AOF
5.如图,∠α的度数等于( )
A.135° B.125° C.115° D.105°
6.如图所示,直线AB和CD相交所成的四个角中,∠1的邻补角是________.
知识点2 对顶角及其性质
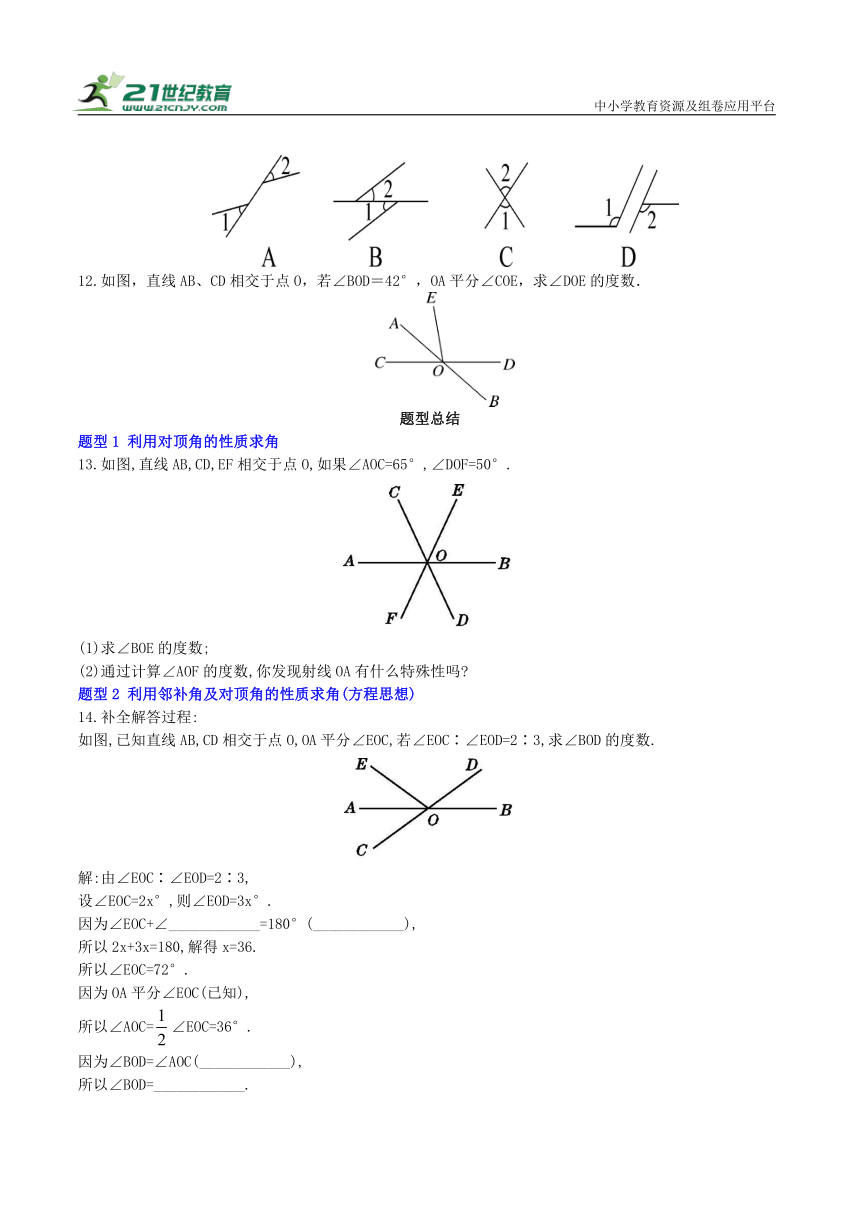
7识别对顶角应同时满足:①有公共___________;②两个角的两边___________.
8.如图,小强和小丽一起玩跷跷板,横板AB绕O上下转动,当小强从A到A'的位置时,∠AOA'=45°,则∠BOB'的度数为___________,理由是___________. 版权所有
9.如图,直线AB,CD相交于点O,则∠1 ∠2,根据的是 ;∠2+∠3= ,根据的是 .
10.下列语句正确的是( )
A.顶点相对的两个角是对顶角
B.有公共顶点并且相等的两个角是对顶角
C.两条直线相交,有公共顶点的两个角是对顶角
D.两条直线相交,有公共顶点且没有公共边的两个角是对顶角
11.下列图形中∠1与∠2互为对顶角的是( )
12.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
题型总结
题型1 利用对顶角的性质求角
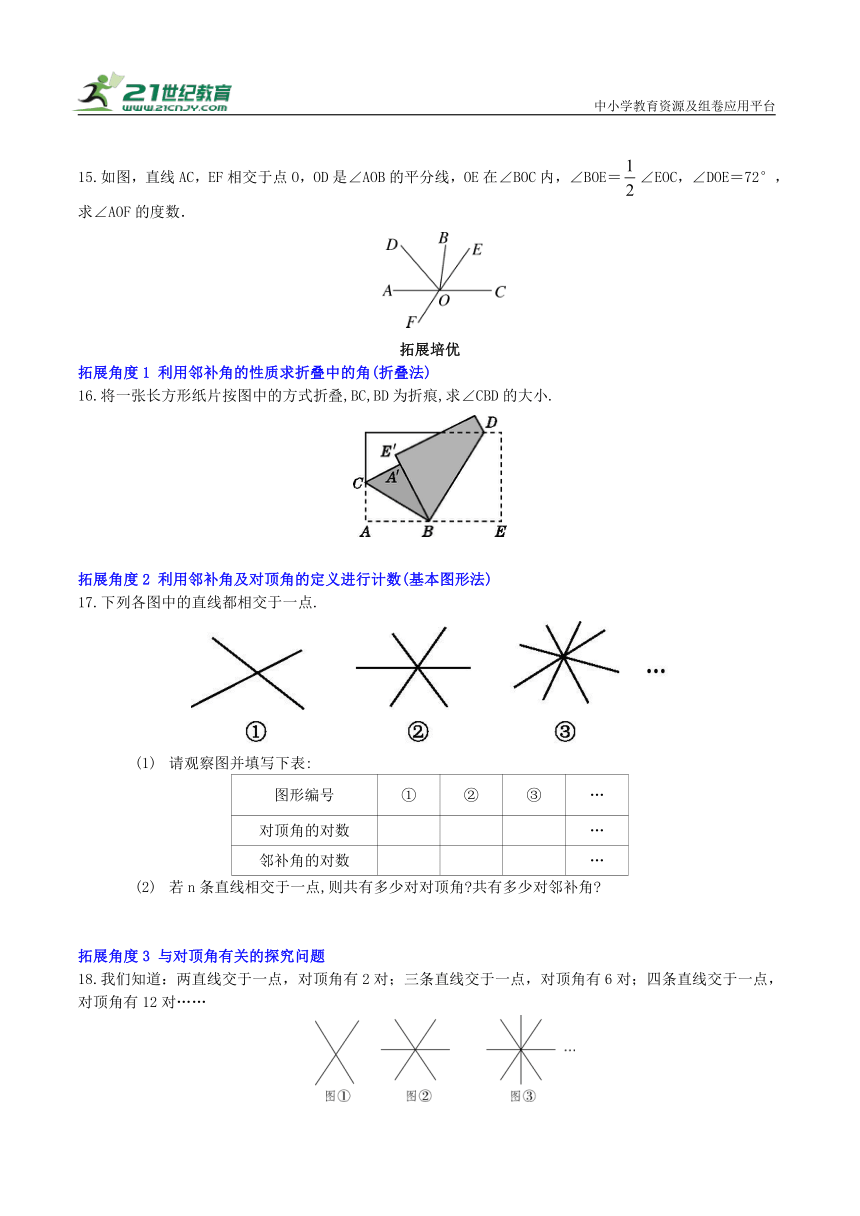
13.如图,直线AB,CD,EF相交于点O,如果∠AOC=65°,∠DOF=50°.
(1)求∠BOE的度数;
(2)通过计算∠AOF的度数,你发现射线OA有什么特殊性吗
题型2 利用邻补角及对顶角的性质求角(方程思想)
14.补全解答过程:
如图,已知直线AB,CD相交于点O,OA平分∠EOC,若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
解:由∠EOC∶∠EOD=2∶3,
设∠EOC=2x°,则∠EOD=3x°.
因为∠EOC+∠____________=180°(____________),
所以2x+3x=180,解得x=36.
所以∠EOC=72°.
因为OA平分∠EOC(已知),
所以∠AOC=∠EOC=36°.
因为∠BOD=∠AOC(____________),
所以∠BOD=____________.
15.如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=∠EOC,∠DOE=72°,求∠AOF的度数.
拓展培优
拓展角度1 利用邻补角的性质求折叠中的角(折叠法)
16.将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD的大小.
拓展角度2 利用邻补角及对顶角的定义进行计数(基本图形法)
17.下列各图中的直线都相交于一点.
请观察图并填写下表:
图形编号 ① ② ③ …
对顶角的对数 …
邻补角的对数 …
若n条直线相交于一点,则共有多少对对顶角 共有多少对邻补角
拓展角度3 与对顶角有关的探究问题
18.我们知道:两直线交于一点,对顶角有2对;三条直线交于一点,对顶角有6对;四条直线交于一点,对顶角有12对……
(1)10条直线交于一点,对顶角有________对;
(2)n(n≥2)条直线交于一点,对顶角有________对.
中小学教育资源及组卷应用平台
5.1 相交线
第1课时 相交线
参考答案与试题解析
夯基训练
知识点1 邻补角
1.识别邻补角应同时满足以下三条:①有公共_____________;②有一条公共边;③两角的另一边_____________. 2
1.【答案】①顶点 ③分别互为反向延长线 ·1·c·n·j·y
2.邻补角是指( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且相等的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.【答案】D
3.下列选项中,∠1与∠2互为邻补角的是( )
【答案】D
解:根据邻补角的定义是有公共顶点且有一条公共边,另一边互为反向延长线的两个角,故选项D正确。
4.如图,∠1的邻补角是( )
A.∠BOC B.∠BOE和∠AOF
C.∠AOF D.∠BOC和∠AOF
4.【答案】B
解:根据邻补角的定义,与∠1有公共顶点且有一条公共边,另一边互为反向延长线的角为∠BOE和∠AOF,故选项B正确。
5.如图,∠α的度数等于( )
A.135° B.125° C.115° D.105°
【答案】A
解:根据邻补角的性质可知。
6.如图所示,直线AB和CD相交所成的四个角中,∠1的邻补角是________.
6.【答案】∠2和∠4
解析:根据邻补角的概念判断:有一个公共顶点、一条公共边,另一边互为延长线.∠1和∠2、∠1和∠4都满足有一个公共顶点和一条公共边,另一边互为延长线,故为邻补角.故答案为∠2和∠4.
方法总结:邻补角的定义包含了两层含义:相邻且互补.但需要注意的是:互为邻补角的两个角一定互补,但互补的角不一定是邻补角.
知识点2 对顶角及其性质
7识别对顶角应同时满足:①有公共___________;②两个角的两边___________.
7.【答案】①顶点 ②分别互为反向延长线
8.如图,小强和小丽一起玩跷跷板,横板AB绕O上下转动,当小强从A到A'的位置时,∠AOA'=45°,则∠BOB'的度数为___________,理由是___________. 版权所有
8.【答案】45°;对顶角相等
9.如图,直线AB,CD相交于点O,则∠1 ∠2,根据的是 ;∠2+∠3= ,根据的是 .
9.【答案】=;对顶角相等;180°;邻补角的定义
10.下列语句正确的是( )
A.顶点相对的两个角是对顶角
B.有公共顶点并且相等的两个角是对顶角
C.两条直线相交,有公共顶点的两个角是对顶角
D.两条直线相交,有公共顶点且没有公共边的两个角是对顶角
10.【答案】D
解:A错误,如图①,∠1与∠2的顶点相对,但∠1与∠2不是对顶角;
B错误,如图②,∠1与∠2有公共顶点,且∠1=∠2,但∠1与∠2不是对顶角;
C错误,如图③,∠1与∠2是两条直线相交且有公共顶点的角,但∠1与∠2不是对顶角;
D正确.
11.下列图形中∠1与∠2互为对顶角的是( )
11.解析:观察∠1与∠2的位置特征,只有C中∠1和∠2同时满足有公共顶点,且∠1的两边是∠2的两边的反向延长线.故选C.
方法总结:判断对顶角只看两点:①有公共顶点;②一个角的两边分别是另一个角的两边的反向延长线.
12.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
12.解析:根据对顶角的性质,可得∠AOC与∠BOD的关系,根据OA平分∠COE,可得∠COE与∠AOC的关系,根据邻补角的性质,可得答案.
解:由对顶角相等得∠AOC=∠BOD=42°.∵OA平分∠COE,∴∠COE=2∠AOC=84°.由邻补角的性质得∠DOE=180°-∠COE=180°-84°=96°.
方法总结:解决此类问题的关键是在图中找出对顶角和邻补角,根据两种角的性质找出已知角和未知角之间的数量关系.
题型总结
题型1 利用对顶角的性质求角
13.如图,直线AB,CD,EF相交于点O,如果∠AOC=65°,∠DOF=50°.
(1)求∠BOE的度数;
(2)通过计算∠AOF的度数,你发现射线OA有什么特殊性吗
13.解:(1)因为∠AOC=65°,
所以∠BOD=∠AOC=65°.
又因为∠BOE+∠BOD+∠DOF=180°,∠DOF=50°,
所以∠BOE=180°-65°-50°=65°.
(2)因为∠AOF=∠BOE=65°,且∠AOC=65°,
所以∠AOF=∠AOC,
所以射线OA是∠COF的平分线.
题型2 利用邻补角及对顶角的性质求角(方程思想)
14.补全解答过程:
如图,已知直线AB,CD相交于点O,OA平分∠EOC,若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
解:由∠EOC∶∠EOD=2∶3,
设∠EOC=2x°,则∠EOD=3x°.
因为∠EOC+∠____________=180°(____________),
所以2x+3x=180,解得x=36.
所以∠EOC=72°.
因为OA平分∠EOC(已知),
所以∠AOC=∠EOC=36°.
因为∠BOD=∠AOC(____________),
所以∠BOD=____________.
14.EOD;平角的定义(邻补角的性质);对顶角相等;36°
15.如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=∠EOC,∠DOE=72°,求∠AOF的度数.
15.解析:因为已知量与未知量的关系较复杂,所以想到列方程解答,根据观察可设∠BOE=x,则∠AOF=∠EOC=2x,然后根据对顶角和邻补角找到等量关系,列方程.
解:设∠BOE=x,则∠AOF=∠EOC=2x.∵∠AOB与∠BOC互为邻补角,∴∠AOB=180°-3x.∵OD平分∠AOB,∴∠DOB=∠AOB=90°-x.∵∠DOE=72°,∴90°-x+x=72°,解得x=36°.∴∠AOF=2x=72°.
方法总结:在相交线中求角的度数时,就要考虑使用对顶角相等或邻补角互补.若已知关系较复杂,比如出现比例或倍分关系时,可列方程解决角度问题.
拓展培优
拓展角度1 利用邻补角的性质求折叠中的角(折叠法)
16.将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD的大小.
16.解:由折叠的性质可知∠ABC=∠A'BC,∠EBD=∠E'BD,所以∠A'BC=∠ABE',∠E'BD=∠EBE'.由∠ABE'与∠EBE'互为邻补角,得∠ABE'+∠EBE'=180°,因此∠CBD=∠A'BC+∠E'BD=∠ABE'+∠EBE'=(∠ABE'+∠EBE')=90°
点拨:此题运用了折叠法,解题时关键要弄清折叠前后哪些角对应相等.
拓展角度2 利用邻补角及对顶角的定义进行计数(基本图形法)
17.下列各图中的直线都相交于一点.
请观察图并填写下表:
图形编号 ① ② ③ …
对顶角的对数 …
邻补角的对数 …
(2)若n条直线相交于一点,则共有多少对对顶角 共有多少对邻补角
17.解:(1)2;6;12;4;12;24
(2)对顶角共有n(n-1)对,邻补角共有2n(n-1)对.
技巧解:巧数图形中对顶角或邻补角的对数:(1)在复杂图形中数对顶角或邻补角的对数时,我们一般先确定图形中包含有几个两条直线相交的基本图形;(2)在每个基本图形中有2对对顶角、4对邻补角,从而计算出所有对顶角、邻补角的对数.
拓展角度3 与对顶角有关的探究问题
18.我们知道:两直线交于一点,对顶角有2对;三条直线交于一点,对顶角有6对;四条直线交于一点,对顶角有12对……
(1)10条直线交于一点,对顶角有________对;
(2)n(n≥2)条直线交于一点,对顶角有________对.
18.解析:(1)仔细观察计算对顶角对数的式子,发现式子不变的部分及变的部分的规律,得出结论,代入数据求解.如图①,两条直线交于一点,图中共有=2对对顶角;如图②,三条直线交于一点,图中共有=6对对顶角;如图③,四条直线交于一点,图中共有=12对对顶角……按这样的规律,10条直线交于一点,那么对顶角共有=90(对).故答案为90;
(2)利用(1)中规律得出答案即可.由(1)得n(n≥2)条直线交于一点,对顶角的对数为=n(n-1).故答案为n(n-1).
方法总结:解决探索规律的问题,应全面分析所给的数据,特别要注意观察符号的变化规律,发现数据的变化特征.
第1课时 相交线
夯基训练
知识点1 邻补角
1.识别邻补角应同时满足以下三条:①有公共_____________;②有一条公共边;③两角的另一边_____________. 2
2.邻补角是指( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且相等的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
3.下列选项中,∠1与∠2互为邻补角的是( )
4.如图,∠1的邻补角是( )
A.∠BOC B.∠BOE和∠AOF
C.∠AOF D.∠BOC和∠AOF
5.如图,∠α的度数等于( )
A.135° B.125° C.115° D.105°
6.如图所示,直线AB和CD相交所成的四个角中,∠1的邻补角是________.
知识点2 对顶角及其性质
7识别对顶角应同时满足:①有公共___________;②两个角的两边___________.
8.如图,小强和小丽一起玩跷跷板,横板AB绕O上下转动,当小强从A到A'的位置时,∠AOA'=45°,则∠BOB'的度数为___________,理由是___________. 版权所有
9.如图,直线AB,CD相交于点O,则∠1 ∠2,根据的是 ;∠2+∠3= ,根据的是 .
10.下列语句正确的是( )
A.顶点相对的两个角是对顶角
B.有公共顶点并且相等的两个角是对顶角
C.两条直线相交,有公共顶点的两个角是对顶角
D.两条直线相交,有公共顶点且没有公共边的两个角是对顶角
11.下列图形中∠1与∠2互为对顶角的是( )
12.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
题型总结
题型1 利用对顶角的性质求角
13.如图,直线AB,CD,EF相交于点O,如果∠AOC=65°,∠DOF=50°.
(1)求∠BOE的度数;
(2)通过计算∠AOF的度数,你发现射线OA有什么特殊性吗
题型2 利用邻补角及对顶角的性质求角(方程思想)
14.补全解答过程:
如图,已知直线AB,CD相交于点O,OA平分∠EOC,若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
解:由∠EOC∶∠EOD=2∶3,
设∠EOC=2x°,则∠EOD=3x°.
因为∠EOC+∠____________=180°(____________),
所以2x+3x=180,解得x=36.
所以∠EOC=72°.
因为OA平分∠EOC(已知),
所以∠AOC=∠EOC=36°.
因为∠BOD=∠AOC(____________),
所以∠BOD=____________.
15.如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=∠EOC,∠DOE=72°,求∠AOF的度数.
拓展培优
拓展角度1 利用邻补角的性质求折叠中的角(折叠法)
16.将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD的大小.
拓展角度2 利用邻补角及对顶角的定义进行计数(基本图形法)
17.下列各图中的直线都相交于一点.
请观察图并填写下表:
图形编号 ① ② ③ …
对顶角的对数 …
邻补角的对数 …
若n条直线相交于一点,则共有多少对对顶角 共有多少对邻补角
拓展角度3 与对顶角有关的探究问题
18.我们知道:两直线交于一点,对顶角有2对;三条直线交于一点,对顶角有6对;四条直线交于一点,对顶角有12对……
(1)10条直线交于一点,对顶角有________对;
(2)n(n≥2)条直线交于一点,对顶角有________对.
中小学教育资源及组卷应用平台
5.1 相交线
第1课时 相交线
参考答案与试题解析
夯基训练
知识点1 邻补角
1.识别邻补角应同时满足以下三条:①有公共_____________;②有一条公共边;③两角的另一边_____________. 2
1.【答案】①顶点 ③分别互为反向延长线 ·1·c·n·j·y
2.邻补角是指( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且相等的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
2.【答案】D
3.下列选项中,∠1与∠2互为邻补角的是( )
【答案】D
解:根据邻补角的定义是有公共顶点且有一条公共边,另一边互为反向延长线的两个角,故选项D正确。
4.如图,∠1的邻补角是( )
A.∠BOC B.∠BOE和∠AOF
C.∠AOF D.∠BOC和∠AOF
4.【答案】B
解:根据邻补角的定义,与∠1有公共顶点且有一条公共边,另一边互为反向延长线的角为∠BOE和∠AOF,故选项B正确。
5.如图,∠α的度数等于( )
A.135° B.125° C.115° D.105°
【答案】A
解:根据邻补角的性质可知。
6.如图所示,直线AB和CD相交所成的四个角中,∠1的邻补角是________.
6.【答案】∠2和∠4
解析:根据邻补角的概念判断:有一个公共顶点、一条公共边,另一边互为延长线.∠1和∠2、∠1和∠4都满足有一个公共顶点和一条公共边,另一边互为延长线,故为邻补角.故答案为∠2和∠4.
方法总结:邻补角的定义包含了两层含义:相邻且互补.但需要注意的是:互为邻补角的两个角一定互补,但互补的角不一定是邻补角.
知识点2 对顶角及其性质
7识别对顶角应同时满足:①有公共___________;②两个角的两边___________.
7.【答案】①顶点 ②分别互为反向延长线
8.如图,小强和小丽一起玩跷跷板,横板AB绕O上下转动,当小强从A到A'的位置时,∠AOA'=45°,则∠BOB'的度数为___________,理由是___________. 版权所有
8.【答案】45°;对顶角相等
9.如图,直线AB,CD相交于点O,则∠1 ∠2,根据的是 ;∠2+∠3= ,根据的是 .
9.【答案】=;对顶角相等;180°;邻补角的定义
10.下列语句正确的是( )
A.顶点相对的两个角是对顶角
B.有公共顶点并且相等的两个角是对顶角
C.两条直线相交,有公共顶点的两个角是对顶角
D.两条直线相交,有公共顶点且没有公共边的两个角是对顶角
10.【答案】D
解:A错误,如图①,∠1与∠2的顶点相对,但∠1与∠2不是对顶角;
B错误,如图②,∠1与∠2有公共顶点,且∠1=∠2,但∠1与∠2不是对顶角;
C错误,如图③,∠1与∠2是两条直线相交且有公共顶点的角,但∠1与∠2不是对顶角;
D正确.
11.下列图形中∠1与∠2互为对顶角的是( )
11.解析:观察∠1与∠2的位置特征,只有C中∠1和∠2同时满足有公共顶点,且∠1的两边是∠2的两边的反向延长线.故选C.
方法总结:判断对顶角只看两点:①有公共顶点;②一个角的两边分别是另一个角的两边的反向延长线.
12.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
12.解析:根据对顶角的性质,可得∠AOC与∠BOD的关系,根据OA平分∠COE,可得∠COE与∠AOC的关系,根据邻补角的性质,可得答案.
解:由对顶角相等得∠AOC=∠BOD=42°.∵OA平分∠COE,∴∠COE=2∠AOC=84°.由邻补角的性质得∠DOE=180°-∠COE=180°-84°=96°.
方法总结:解决此类问题的关键是在图中找出对顶角和邻补角,根据两种角的性质找出已知角和未知角之间的数量关系.
题型总结
题型1 利用对顶角的性质求角
13.如图,直线AB,CD,EF相交于点O,如果∠AOC=65°,∠DOF=50°.
(1)求∠BOE的度数;
(2)通过计算∠AOF的度数,你发现射线OA有什么特殊性吗
13.解:(1)因为∠AOC=65°,
所以∠BOD=∠AOC=65°.
又因为∠BOE+∠BOD+∠DOF=180°,∠DOF=50°,
所以∠BOE=180°-65°-50°=65°.
(2)因为∠AOF=∠BOE=65°,且∠AOC=65°,
所以∠AOF=∠AOC,
所以射线OA是∠COF的平分线.
题型2 利用邻补角及对顶角的性质求角(方程思想)
14.补全解答过程:
如图,已知直线AB,CD相交于点O,OA平分∠EOC,若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
解:由∠EOC∶∠EOD=2∶3,
设∠EOC=2x°,则∠EOD=3x°.
因为∠EOC+∠____________=180°(____________),
所以2x+3x=180,解得x=36.
所以∠EOC=72°.
因为OA平分∠EOC(已知),
所以∠AOC=∠EOC=36°.
因为∠BOD=∠AOC(____________),
所以∠BOD=____________.
14.EOD;平角的定义(邻补角的性质);对顶角相等;36°
15.如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=∠EOC,∠DOE=72°,求∠AOF的度数.
15.解析:因为已知量与未知量的关系较复杂,所以想到列方程解答,根据观察可设∠BOE=x,则∠AOF=∠EOC=2x,然后根据对顶角和邻补角找到等量关系,列方程.
解:设∠BOE=x,则∠AOF=∠EOC=2x.∵∠AOB与∠BOC互为邻补角,∴∠AOB=180°-3x.∵OD平分∠AOB,∴∠DOB=∠AOB=90°-x.∵∠DOE=72°,∴90°-x+x=72°,解得x=36°.∴∠AOF=2x=72°.
方法总结:在相交线中求角的度数时,就要考虑使用对顶角相等或邻补角互补.若已知关系较复杂,比如出现比例或倍分关系时,可列方程解决角度问题.
拓展培优
拓展角度1 利用邻补角的性质求折叠中的角(折叠法)
16.将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD的大小.
16.解:由折叠的性质可知∠ABC=∠A'BC,∠EBD=∠E'BD,所以∠A'BC=∠ABE',∠E'BD=∠EBE'.由∠ABE'与∠EBE'互为邻补角,得∠ABE'+∠EBE'=180°,因此∠CBD=∠A'BC+∠E'BD=∠ABE'+∠EBE'=(∠ABE'+∠EBE')=90°
点拨:此题运用了折叠法,解题时关键要弄清折叠前后哪些角对应相等.
拓展角度2 利用邻补角及对顶角的定义进行计数(基本图形法)
17.下列各图中的直线都相交于一点.
请观察图并填写下表:
图形编号 ① ② ③ …
对顶角的对数 …
邻补角的对数 …
(2)若n条直线相交于一点,则共有多少对对顶角 共有多少对邻补角
17.解:(1)2;6;12;4;12;24
(2)对顶角共有n(n-1)对,邻补角共有2n(n-1)对.
技巧解:巧数图形中对顶角或邻补角的对数:(1)在复杂图形中数对顶角或邻补角的对数时,我们一般先确定图形中包含有几个两条直线相交的基本图形;(2)在每个基本图形中有2对对顶角、4对邻补角,从而计算出所有对顶角、邻补角的对数.
拓展角度3 与对顶角有关的探究问题
18.我们知道:两直线交于一点,对顶角有2对;三条直线交于一点,对顶角有6对;四条直线交于一点,对顶角有12对……
(1)10条直线交于一点,对顶角有________对;
(2)n(n≥2)条直线交于一点,对顶角有________对.
18.解析:(1)仔细观察计算对顶角对数的式子,发现式子不变的部分及变的部分的规律,得出结论,代入数据求解.如图①,两条直线交于一点,图中共有=2对对顶角;如图②,三条直线交于一点,图中共有=6对对顶角;如图③,四条直线交于一点,图中共有=12对对顶角……按这样的规律,10条直线交于一点,那么对顶角共有=90(对).故答案为90;
(2)利用(1)中规律得出答案即可.由(1)得n(n≥2)条直线交于一点,对顶角的对数为=n(n-1).故答案为n(n-1).
方法总结:解决探索规律的问题,应全面分析所给的数据,特别要注意观察符号的变化规律,发现数据的变化特征.
